数据结构之二叉树
🎈一.二叉树相关概念
1.树
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合,树结构通常用来存储逻辑关系为 "一对多" 的数据。例如:
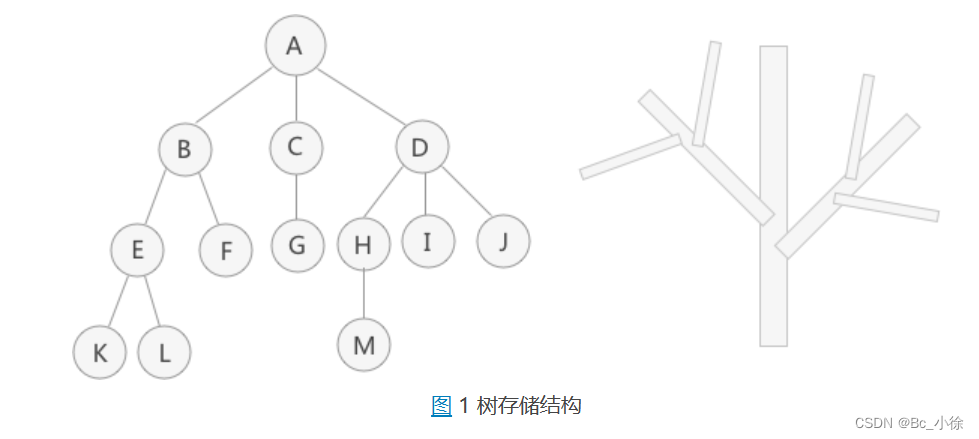
关于树的几个重要概念:
1)树的度:一棵树中,所有结点度的最大值称为树的度,如上图,这棵树的度为3;
2)节点的度:一个结点含有子树的个数称为该结点的度,如上图,A节点的度为3;
3)根节点:一棵树中,没有双亲结点的结点,如上图,A就是根节点;
4)叶子节点:简单来说,度为0的就是叶子节点,如上图,K,L,F,M等都是叶子节点;
5)树的高度或深度:树中结点的最大层次,如上图,树的高度为4;
那么什么是二叉树呢?
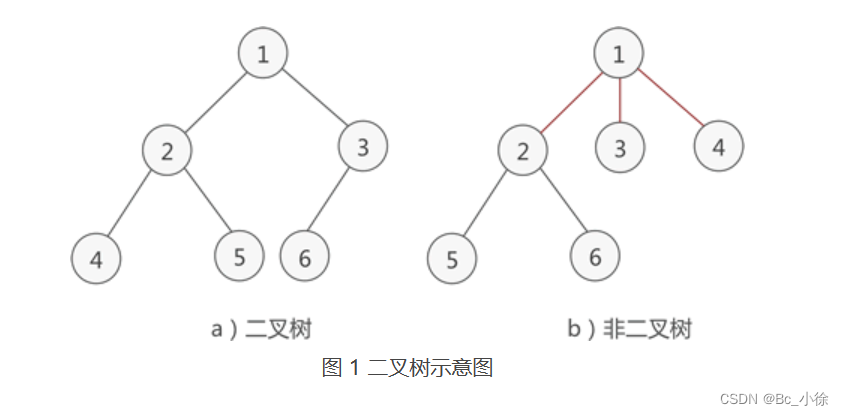
简单地理解,满足以下两个条件的树就是二叉树:
- 本身是有序树;
- 树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2;
如图:
🎈二.二叉树的性质
1.若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有 2^i-1(i>0)个结点;
2.若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是2^k-1 (k>=0);
3. 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1;
✅关于此结论的推导:
对于任意一棵二叉树,一棵有N个节点的树就有N-1条边
假设度为0的节点为n0,度为1的节点为n1,度为2的节点为n2,度为0的节点没有边,度为1的节点有1条边,度为2的节点有2条边,由此可得:
N-1=n1*1+n2*2 ----------------产生的边的关系
N=n0+n1+n2 ----------------产生节点的关系
联立就可以得出这个结论:n0=n2+1
4.具有n个结点的完全二叉树的深度k为 log2(n+1)上取整;
✅习题:
1) 在具有 2n 个结点的完全二叉树中,叶子结点个数为(A);
A .n B. n+1 C. n-1 D. n/2
解析: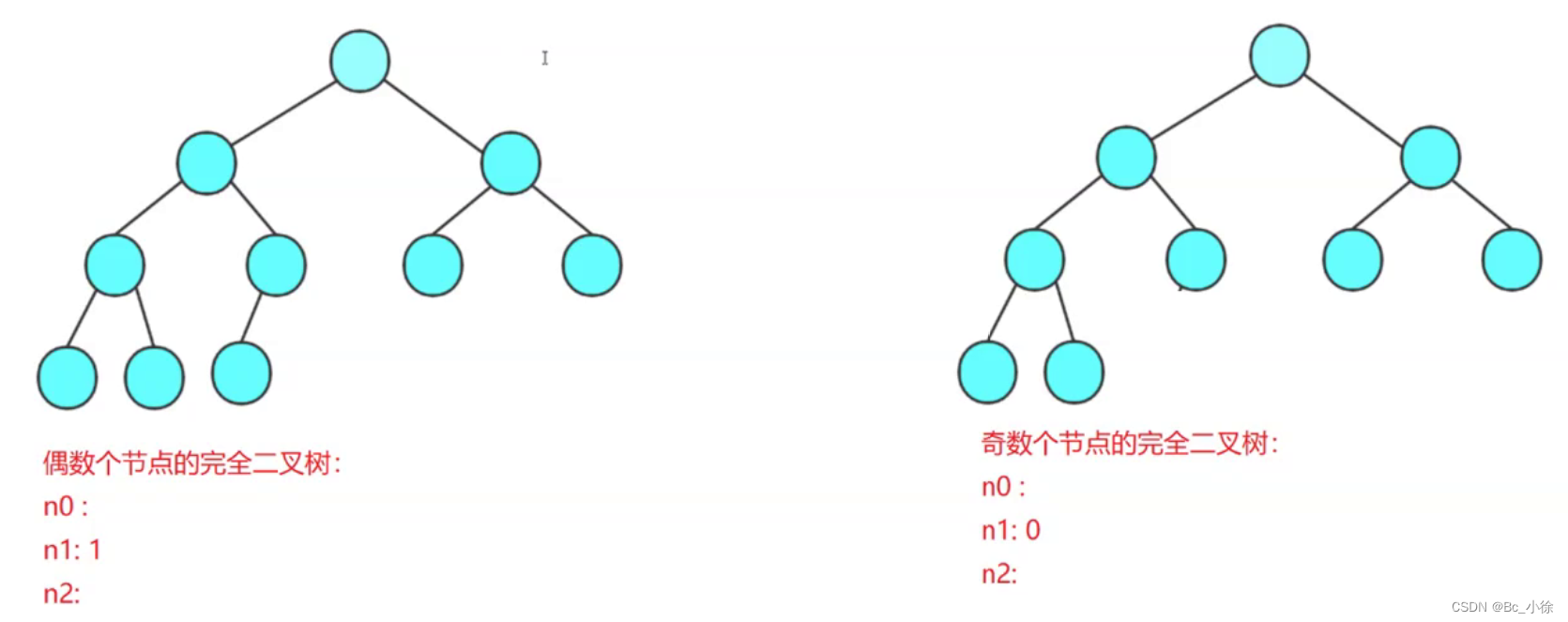
完全二叉树分奇偶数俩种情况,如上图,本题有2n个节点,是偶数,那么度为1的节点数只有1个,所以可知:
2n=n0+n1+n2;
n0=n2+1;
代入可求:n0=n;
2)一个具有767个节点的完全二叉树,其叶子节点个数为(B);
A. 383 B. 384 C. 385 D. 386
解析:因为它是一棵完全二叉树,节点数为奇数,说明它是一棵满二叉树,所以没有度为1的节点,由此可知:
767=n0+n2;
n0=n2+1;
联立上式可以求出答案
🎈三.构造二叉树
二叉树的存储结构分为:顺序存储和类似于链表的链式存储。
构造一个类,里面存放左子树,右子树,数据域;
public static class TreeNode {public char val;//数据域public TreeNode left;//左节点public TreeNode right;//右节点public TreeNode(char val) {this.val = val;}}//构造树public TreeNode createTree() {TreeNode node1 = new TreeNode('A');TreeNode node2 = new TreeNode('B');TreeNode node3 = new TreeNode('C');TreeNode node4 = new TreeNode('D');TreeNode node5 = new TreeNode('E');TreeNode node6 = new TreeNode('F');TreeNode node7 = new TreeNode('G');node1.left = node2;node1.right = node3;node2.left = node4;node2.right = node5;node3.left = node6;node3.right = node7;return node1;}
}🎈四.二叉树的相关操作
1.前序遍历
前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点--->根的左子树--->根的右子树。
//前序遍历public void preOrder(TreeNode root) {if (root == null) {return;}System.out.print(root.val + " ");preOrder(root.left);preOrder(root.right);}2.中序遍历
中序遍历(Inorder Traversal)——根的左子树--->根节点--->根的右子树。
//中序遍历public void inOrder(TreeNode root) {if (root == null) {return;}inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);}3.后序遍历
后序遍历(Postorder Traversal)——根的左子树--->根的右子树--->根节点。
//后序遍历public void postOrder(TreeNode root) {if (root == null) {return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val + " ");}4.获取书中节点的个数
// 获取树中节点的个数public int size(TreeNode root) {if (root == null) {return 0;}int leftSize = size(root.left);int rightSize = size(root.right);return leftSize + rightSize + 1;//个数=左树的节点树+右树的节点树+1}5.获取叶子节点数
// 获取叶子节点的个数public int getLeafNodeCount(TreeNode root) {if (root == null) {return 0;}if (root.left == null && root.right == null) {return 1;//如果左右两边都为空,那么一定是叶子节点}int leftSize = getLeafNodeCount(root.left);int rightSize = getLeafNodeCount(root.right);return leftSize + rightSize;}6.获取第k层的节点数
// 获取第K层节点的个数public int getKLevelNodeCount(TreeNode root, int k) {if (root == null) {return 0;}if (k == 1) {return 1;}int leftSize = getKLevelNodeCount(root.left, k - 1);int rightSize = getKLevelNodeCount(root.right, k - 1);return leftSize + rightSize;}7.获取二叉树的高度
// 获取二叉树的高度public int getHeight(TreeNode root) {if (root == null) {return 0;}int leftHeight = getHeight(root.left);int rightHeight = getHeight(root.right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}8.查找value值是否存在树中
// 检测值为value的元素是否存在public TreeNode find(TreeNode root, int val) {if (root == null) {return null;}if (val == root.val) {return root;}TreeNode leftTree = find(root.left, val);if (leftTree != null) {return leftTree;}TreeNode rightTree = find(root.right, val);if (rightTree != null) {return rightTree;}return null;}相关文章:

数据结构之二叉树
🎈一.二叉树相关概念 1.树 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合,树结构通常用来存储逻辑关系为 "一对多" 的数据。例如: 关于树的几个重要概念&…...
上海亚商投顾:三大指数集体调整 消费板块逆市活跃
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。市场情绪三大指数今日集体调整,沪指全天弱势震荡,创业板指盘中跌超1%。旅游、食品、乳业等大消费板块…...
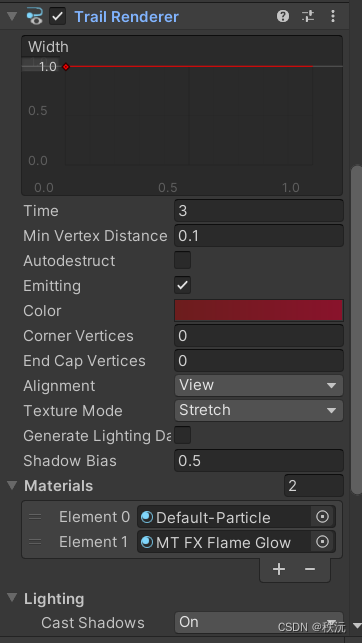
【2023unity游戏制作-mango的冒险】-开始画面API制作
👨💻个人主页:元宇宙-秩沅 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 秩沅 原创 收录于专栏:游戏制作 ⭐mango的冒险-开始画面制作⭐ 文章目录⭐mango的冒险-开始画面制作⭐👨&…...

【微服务】Nacos配置管理
🚩本文已收录至专栏:微服务探索之旅 👍希望您能有所收获 Nacos除了可以做配置管理,同样可以当作注册中心来使用。 了解注册中心用法点击跳转👉【微服务】Nacos注册中心 一.引入 当微服务部署的实例越来越多࿰…...
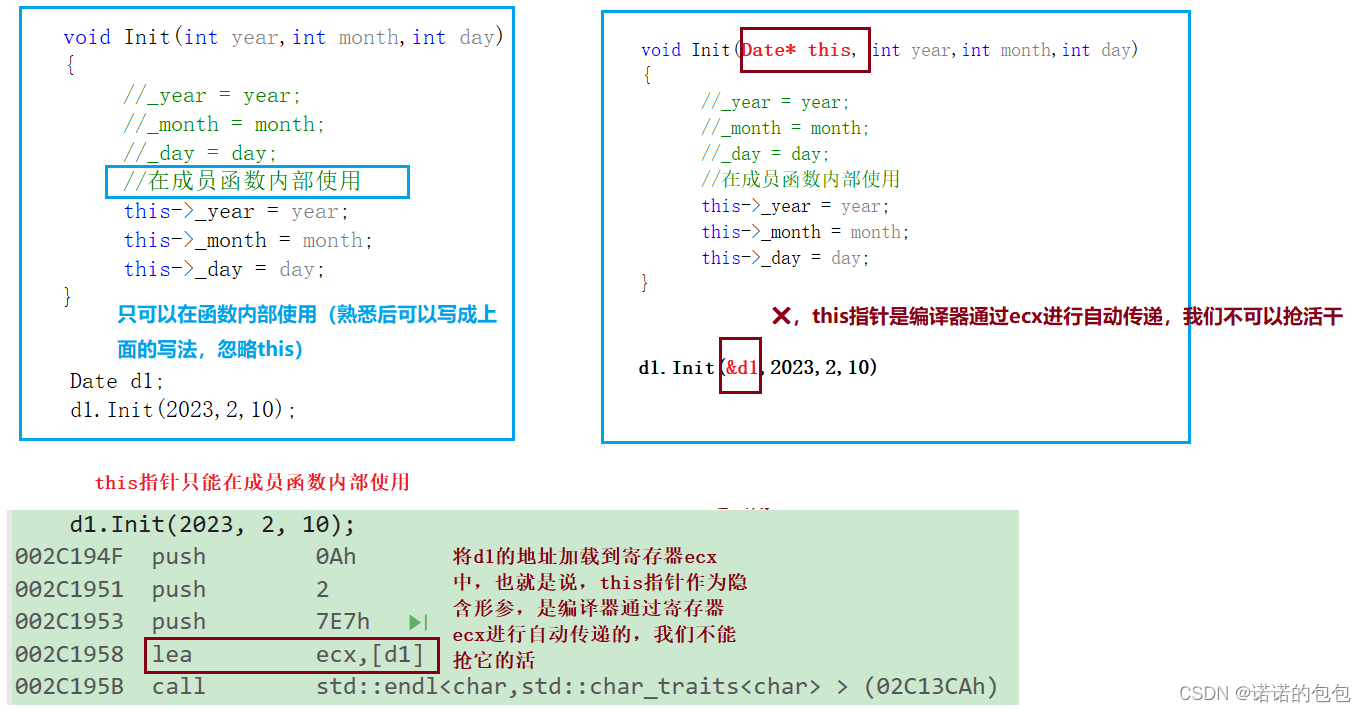
【C++】类与对象理解和学习(上)
专栏放在【C知识总结】,会持续更新,期待支持🌹类是什么?类是对对象进行描述的,是一个模型一样的东西,限定了类有哪些成员,定义出一个类并没有分配实际的内存空间来存储它(实例化后才…...
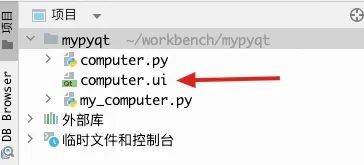
Pyqt5小案例,界面与逻辑分离的小计算器程序
直接看下最终效果: 使用技术总结 使用Designer设计界面 使用pyuic5命令导出到python文件 新建逻辑处理文件,继承pyuic5导出的文件的类,在里面编写信号与槽的处理逻辑 使用Designer设计界面 要使用Designer,安装一个Python库即…...

leaflet加载KML文件,显示图形(方法2)
第049个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中加载KML文件,将图形显示在地图上。 直接复制下面的 vue+openlayers源代码,操作2分钟即可运行实现效果; 注意如果OpenStreetMap无法加载,请加载其他来练习 文章目录 示例效果配置方式示例源代码(共66…...

Mysql 部署 MGR 集群
0. 参考文章 官方文档: MySQL :: MySQL 8.0 Reference Manual :: 18.2 Getting Started 博客: MGR 单主模式部署教程(基于 MySQL 8.0.28) - 墨天轮 (modb.pro) mysql MGR单主模式的搭建 - 墨天轮 (modb.pro) MySQL 5.7 基于…...

迁移至其他美国主机商时需要考虑的因素
网站的可访问性是关系业务的关键因素之一。一个稳定、快速且优化良好的主机上的网站更有可能享受不间断的流量,并在谷歌的SERP中获得更好的排名。因此,在构建企业网站时,选择合适的主机商相当重要。不过就以美国主机为例,由于每个…...

【数据结构】第二章 线性表
文章目录第二章 知识体系2.1 线性表的定义和基本操作2.1.1 线性表的定义2.1.2 线性表的基本操作2.2 线性表的顺序表示2.2.1 顺序表的定义2.2.2 顺序表的基本操作的实现2.3 线性表的链式表示2.3.1 单链表的定义2.3.2 单链表的基本操作实现2.3.3 双链表2.3.4 循环链表2.3.5 静态链…...
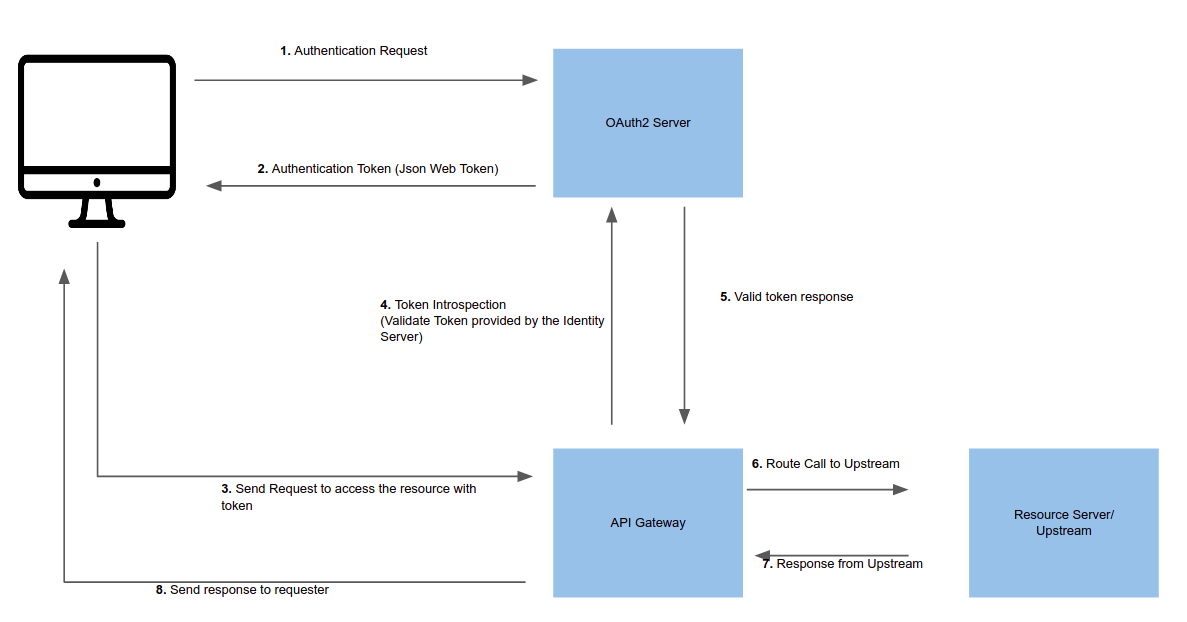
RESTful API 为何成为顶流 API 架构风格?
作者孙毅,API7.ai 技术工程师,Apache APISIX Committer 万物互联的世界充满着各式各样的 API ,如何统筹规范 API 至关重要。RESTful API 是目前世界上最流行的 API 架构风格之一,它可以帮助你实现客户端与服务端关注点分离&#x…...
)
Python基础知识点汇总(列表)
列表的含义 列表由一系列按特定顺序排列的元素组成,是Python中内置的可变序列。 **注:**列表的所有元素放在中括号[]中,相邻的两个元素用逗号分隔; 可将整数、实数、字符串、列表、元组等任何类型的内容放到列表中,且同一列表的元素类型可以不同。 列表的创建和删除 1.…...
新的一年软件测试行业的趋势能够更好?
如果说,2022年对于全世界来说,都是一场极大的挑战的话;那么,2023年绝对是机遇多多的一年。众所周知,随着疫情在全球范围内逐步得到控制,无论是国际还是国内的环境,都会呈现逐步回升的趋势&#…...

Threejs中的Shadow Mapping(阴影贴图)
简而言之,步骤如下: 1.从灯光位置视点(阴影相机)创建深度图。 2.从相机的位置角度进行屏幕渲染,在每个像素点,比较由阴影相机的MVP矩阵计算的深度值和深度图的值的大小,如果深度图值小的话&…...
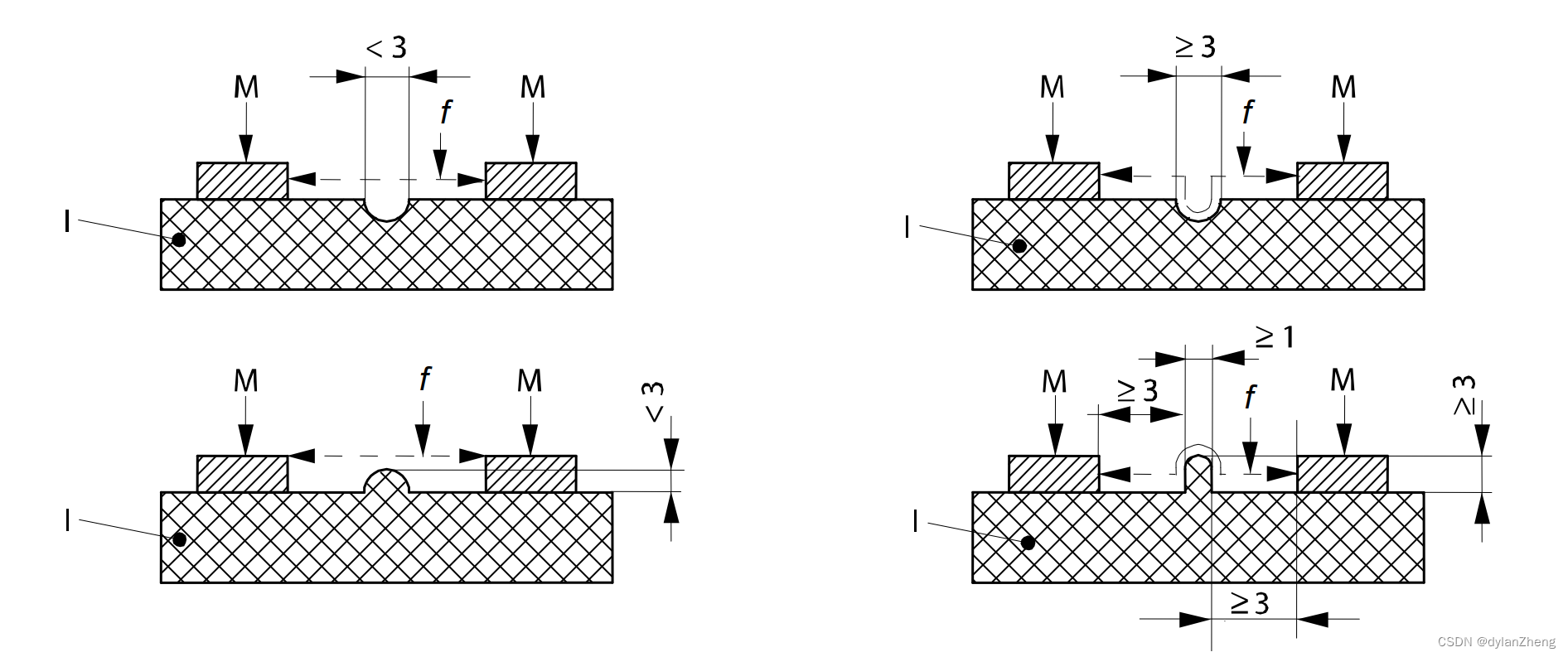
本质安全设备标准(IEC60079-11)的理解(四)
本质安全设备标准(IEC60079-11)的理解(四) 对于标准中“Separation”的理解 IEC60079-11使用了较长的篇幅来说明设计中需要考虑到的各种间距, 这也从一定程度上说明了间距比较重要,在设计中是需要认真考虑…...

(record)QEMU安装最小linux系统——TinyCore(命令行版)
文章目录QEMU安装最小linux系统——TinyCore参考QEMU使用qemu创建tinycore虚拟机再次启动文件保存QEMU安装最小linux系统——TinyCore 简单记录安装过程和记录点 参考 [原创] qemu 与 Tiny Core tinycore的探索 QEMU qemu不多介绍,这里是在WSL2上安装的linux版…...

C++中的cast类型转换
reinterpret_cast用法:reinpreter_cast<type-id> (expression)type-id必须是一个指针、引用、算术类型、函数指针或者成员指针。它可以把一个指针转换成一个整数,也可以把一个整数转换成一个指针。这个操作符能够在非相关的类型之间转换。操作结果…...

西瓜数据集读取的详细解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。喜欢通过博客创作的方式对所学的知识进行总结与归纳,不仅形成深入且独到的理…...

Mac开发环境配置
一、mac 安装homebrew 1. 必要性 homebrew可以通过bash命令快速安装配置开发环境,并且在大多数情况下可以实现环境的自动配置。(一键安装配置) 2. 收益 节省开发环境工具配置时间,提高人效。 3. 安装步骤 打开mac终端…...

概率论面试题1:玫瑰花
概率论面试题 1. 一个活动,n个女生手里拿着长短不一的玫瑰花,无序的排成一排,一个男生从头走到尾,试图拿更长的玫瑰花,一旦拿了一朵就不能再拿其他的,错过了就不能回头,问最好的策略࿱…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
