【Math】导数、梯度、雅可比矩阵、黑塞矩阵
导数、梯度、雅可比矩阵、黑塞矩阵都是与求导相关的一些概念,比较容易混淆,本文主要是对它们的使用场景和定义进行区分。
首先需要先明确一些函数的叫法(是否多元,以粗体和非粗体进行区分):
一元函数: f ( x ) : R ⟶ R f(x):\mathbb{R} \longrightarrow \mathbb{R} f(x):R⟶R多元函数: f ( x ) : R n ⟶ R f(\mathbf{x}):\mathbb{R}^{n} \longrightarrow \mathbb{R} f(x):Rn⟶R向量函数: f ( x ) : R n ⟶ R m \mathbf{f(x)}:\mathbb{R}^{n} \longrightarrow \mathbb{R}^{m} f(x):Rn⟶Rm
例如:
- 函数 y = x y=x y=x为一元函数
- 函数 y = x 1 + 2 x 2 y=x_1+2x_2 y=x1+2x2为多元函数
- 函数 { y 1 = x 1 + 2 x 2 y 2 = 2 x 1 + x 2 \begin{cases} y_1 =x_1+2x_2 \\ y_2=2x_1+x_2 \end{cases} {y1=x1+2x2y2=2x1+x2为向量函数
概念详解
导数
针对一元函数: f ( x ) : R ⟶ R f(x):\mathbb{R} \longrightarrow \mathbb{R} f(x):R⟶R,近似:
f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) f(x)\approx f(x_{0})+f^{\prime}(x_{0})(x-x_{0}) f(x)≈f(x0)+f′(x0)(x−x0)
梯度
针对多元函数: f ( x ) : R n ⟶ R f(\mathbf{x}):\mathbb{R}^{n} \longrightarrow \mathbb{R} f(x):Rn⟶R,是导数的推广, 它的结果是一个向量:
▽ f = [ ∂ f ∂ x 1 ∂ f ∂ x 2 . . . ∂ f ∂ x n ] \bigtriangledown f=\begin{bmatrix} \frac{\partial f}{\partial x_{1}} \\ \frac{\partial f}{\partial x_{2}} \\ ... \\ \frac{\partial f}{\partial x_{n}} \end{bmatrix} ▽f= ∂x1∂f∂x2∂f...∂xn∂f
近似:
f ( x ) ≈ f ( x 0 ) + ▽ f ( x 0 ) ( x − x 0 ) f(\mathbf{x} )\approx f(\mathbf{x}_{0})+\bigtriangledown f(\mathbf{x}_{0})(\mathbf{x}-\mathbf{x}_{0}) f(x)≈f(x0)+▽f(x0)(x−x0)
雅可比矩阵
针对向量函数: f ( x ) : R n ⟶ R m \mathbf{f(x)}:\mathbb{R}^{n} \longrightarrow \mathbb{R}^{m} f(x):Rn⟶Rm
如果函数 f ( x ) : R n ⟶ R m \mathbf{f(x)}:\mathbb{R}^{n} \longrightarrow \mathbb{R}^{m} f(x):Rn⟶Rm在点 x \mathbf{x} x处可微的话,在点 x \mathbf{x} x的雅可比矩阵即为该函数在该点的最佳线性逼近,也代表雅可比矩阵是一元函数的导数在向量函数的推广。在这种情况下,雅可比矩阵也被称作函数 f \mathbf{f} f在点 x \mathbf{x} x的微分或者导数,其中行数为 f \mathbf{f} f的维数;列数为 x \mathbf{x} x的维度。
J = [ ∂ f ∂ x 1 . . . ∂ f ∂ x n ] = [ ∂ f 1 ∂ x 1 . . . ∂ f 1 ∂ x n ⋮ ⋱ ⋮ ∂ f m ∂ x 1 . . . ∂ f m ∂ x n ] \mathbf{J}=\begin{bmatrix} \frac{\partial \mathbf{f}}{\partial x_{1}} & ... & \frac{\partial \mathbf{f}}{\partial x_{n}} \end{bmatrix} = \begin{bmatrix} \frac{\partial f_{1}}{\partial x_{1}} & ... & \frac{\partial f_{1}}{\partial x_{n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_{m}}{\partial x_{1}} & ... & \frac{\partial f_{m}}{\partial x_{n}} \end{bmatrix} J=[∂x1∂f...∂xn∂f]= ∂x1∂f1⋮∂x1∂fm...⋱...∂xn∂f1⋮∂xn∂fm
矩阵分量:
J i j = ∂ f i ∂ x j \mathbf{J}_{ij}=\frac{\partial f_{i}}{\partial x_{j}} Jij=∂xj∂fi
近似:
f ( x ) ≈ f ( x 0 ) + J ( x 0 ) ( x − x 0 ) \mathbf{f}(\mathbf{x} )\approx \mathbf{f}(\mathbf{x}_{0})+ \mathbf{J}(\mathbf{x}_{0})(\mathbf{x}-\mathbf{x}_{0}) f(x)≈f(x0)+J(x0)(x−x0)
黑塞矩阵
针对多元函数: f : R n ⟶ R f:\mathbb{R}^{n} \longrightarrow \mathbb{R} f:Rn⟶R,有点二阶导数的意思。
H = [ ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 . . . ∂ 2 f ∂ x 1 ∂ x n ∂ 2 f ∂ x 2 ∂ x 1 ∂ 2 f ∂ x 2 2 . . . ∂ 2 f ∂ x 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ 2 f ∂ x n ∂ x 1 ∂ 2 f ∂ x n ∂ x 2 . . . ∂ 2 f ∂ x n 2 ] \mathbf{H}=\begin{bmatrix} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1}\partial x_{2}} & ... & \frac{\partial^{2} f}{\partial x_{1}\partial x_{n}} \\ \frac{\partial^{2} f}{\partial x_{2}\partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} & ... & \frac{\partial^{2} f}{\partial x_{2}\partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f}{\partial x_{n}\partial x_{1}} & \frac{\partial^{2} f}{\partial x_{n}\partial x_{2}} & ... & \frac{\partial^{2} f}{\partial x_{n}^{2}} \end{bmatrix} H= ∂x12∂2f∂x2∂x1∂2f⋮∂xn∂x1∂2f∂x1∂x2∂2f∂x22∂2f⋮∂xn∂x2∂2f......⋱...∂x1∂xn∂2f∂x2∂xn∂2f⋮∂xn2∂2f
矩阵分量:
H i j = ∂ 2 f ∂ x i ∂ x j \mathbf{H}_{ij}=\frac{\partial^{2} f}{\partial x_{i}\partial x_{j}} Hij=∂xi∂xj∂2f
近似:
f ( x ) ≈ f ( x 0 ) + ▽ f ( x 0 ) ( x − x 0 ) + 1 2 ( x − x 0 ) T H ( x 0 ) ( x − x 0 ) f(\mathbf{x} )\approx f(\mathbf{x}_{0})+\bigtriangledown f(\mathbf{x}_{0})(\mathbf{x}-\mathbf{x}_{0}) + \frac{1}{2}(\mathbf{x}-\mathbf{x}_{0})^{T}\mathbf{H}(\mathbf{x}_{0})(\mathbf{x}-\mathbf{x}_{0}) f(x)≈f(x0)+▽f(x0)(x−x0)+21(x−x0)TH(x0)(x−x0)
实例
对于最简单的一元函数 y = 2 x y=2x y=2x,则该一元函数的导数为: y ′ = 2 y^{\prime}=2 y′=2。这是最基础的了。
对于一个多元函数 y = x 1 4 x 2 + 3 x 2 + x 2 e x 3 y=x_1^4x_2+3x_2+x_2e^{x_3} y=x14x2+3x2+x2ex3,则:
该多元函数的梯度为:
▽ = [ ∂ y ∂ x 1 ∂ y ∂ x 2 ∂ y ∂ x 3 ] = [ 4 x 1 3 x 2 x 1 4 + 3 + e x 3 x 2 e x 3 ] \bigtriangledown =\begin{bmatrix} \frac{\partial y}{\partial x_1} \\ \frac{\partial y}{\partial x_2} \\ \frac{\partial y}{\partial x_3} \end{bmatrix}=\begin{bmatrix} 4x_1^3x_2 \\ x_1^4+3+e^{x_3} \\ x_2e^{x_3}\end{bmatrix} ▽= ∂x1∂y∂x2∂y∂x3∂y = 4x13x2x14+3+ex3x2ex3
该多元函数的黑塞矩阵为:
H = [ ∂ 2 y ∂ x 1 2 ∂ 2 y ∂ x 1 ∂ x 2 ∂ 2 y ∂ x 1 ∂ x 3 ∂ 2 y ∂ x 2 ∂ x 1 ∂ 2 y ∂ x 2 2 ∂ 2 y ∂ x 2 ∂ x 3 ∂ 2 y ∂ x 3 ∂ x 1 ∂ 2 y ∂ x 3 ∂ x 2 ∂ 2 y ∂ x 3 2 ] = [ 12 x 1 2 x 2 4 x 1 3 0 4 x 1 3 0 e x 3 0 e x 3 x 2 e x 3 ] \mathbf{H}=\begin{bmatrix} \frac{\partial^{2} y}{\partial x_{1}^{2}} & \frac{\partial^{2} y}{\partial x_{1}\partial x_{2}} & \frac{\partial^{2} y}{\partial x_{1}\partial x_{3}} \\ \frac{\partial^{2} y}{\partial x_{2}\partial x_{1}} & \frac{\partial^{2} y}{\partial x_{2}^{2}} & \frac{\partial^{2} y}{\partial x_{2}\partial x_{3}} \\ \frac{\partial^{2} y}{\partial x_{3}\partial x_{1}} & \frac{\partial^{2} y}{\partial x_{3}\partial x_{2}} & \frac{\partial^{2} y}{\partial x_{3}^{2}} \end{bmatrix} = \begin{bmatrix} 12x_1^2x_2 & 4x_1^3 & 0\\ 4x_1^3 & 0 & e^{x_3}\\ 0 & e^{x_3} & x_2e^{x_3} \end{bmatrix} H= ∂x12∂2y∂x2∂x1∂2y∂x3∂x1∂2y∂x1∂x2∂2y∂x22∂2y∂x3∂x2∂2y∂x1∂x3∂2y∂x2∂x3∂2y∂x32∂2y = 12x12x24x1304x130ex30ex3x2ex3
视该多元函数的梯度为一个向量函数,即:
{ y 1 = 4 x 1 3 x 2 y 2 = x 1 4 + 3 + e x 3 y 3 = x 2 e x 3 \begin{cases} y_1 =4x_1^3x_2 \\ y_2=x_1^4+3+e^{x_3} \\ y_3=x_2e^{x_3} \end{cases} ⎩ ⎨ ⎧y1=4x13x2y2=x14+3+ex3y3=x2ex3
那么,该多元函数的雅可比矩阵为:
J = [ ∂ y 1 ∂ x 1 ∂ y 1 ∂ x 2 ∂ y 1 ∂ x 3 ∂ y 2 ∂ x 1 ∂ y 2 ∂ x 2 ∂ y 2 ∂ x 3 ∂ y 3 ∂ x 1 ∂ y 3 ∂ x 2 ∂ y 3 ∂ x 3 ] = [ 12 x 1 2 x 2 4 x 1 3 0 4 x 1 3 0 e x 3 0 e x 3 x 2 e x 3 ] \mathbf{J}= \begin{bmatrix} \frac{\partial y_{1}}{\partial x_{1}} & \frac{\partial y_{1}}{\partial x_{2}} & \frac{\partial y_{1}}{\partial x_{3}} \\ \frac{\partial y_{2}}{\partial x_{1}} & \frac{\partial y_{2}}{\partial x_{2}} & \frac{\partial y_{2}}{\partial x_{3}} \\ \frac{\partial y_{3}}{\partial x_{1}} & \frac{\partial y_{3}}{\partial x_{2}} & \frac{\partial y_{3}}{\partial x_{3}} \end{bmatrix} = \begin{bmatrix} 12x_1^2x_2 & 4x_1^3 & 0\\ 4x_1^3 & 0 & e^{x_3}\\ 0 & e^{x_3} & x_2e^{x_3} \end{bmatrix} J= ∂x1∂y1∂x1∂y2∂x1∂y3∂x2∂y1∂x2∂y2∂x2∂y3∂x3∂y1∂x3∂y2∂x3∂y3 = 12x12x24x1304x130ex30ex3x2ex3
可以看出,黑塞矩阵是多元函数 f ( x ) f(\mathbf{x}) f(x)的梯度对自变量 x \mathbf{x} x的雅可比矩阵。
总结
- 梯度是雅可比矩阵的一个特例:当向量函数为标量函数时( f \mathbf{f} f向量维度为1),雅可比矩阵是梯度向量
- 黑塞矩阵是多元函数 f ( x ) f(\mathbf{x}) f(x)的梯度对自变量 x \mathbf{x} x的雅可比矩阵
相关阅读
- 多元函数的泰勒(Taylor)展开式
- 梯度vs Jacobian矩阵vs Hessian矩阵
- 导数、梯度、 Jacobian、Hessian
相关文章:

【Math】导数、梯度、雅可比矩阵、黑塞矩阵
导数、梯度、雅可比矩阵、黑塞矩阵都是与求导相关的一些概念,比较容易混淆,本文主要是对它们的使用场景和定义进行区分。 首先需要先明确一些函数的叫法(是否多元,以粗体和非粗体进行区分): 一元函数&…...

【C语言】——调试技巧
目录 编辑 ①前言 1.什么是Bug? 2.什么是调试? 2.1调试的基本步骤 2.2Release与Debug 3.常用快捷键 4.如何写出好的代码 4.1常见的coding技巧 👉assert() 👉const() const修饰指针: ①前言 调试是每个程序员都…...
【Python】pytorch,CUDA是否可用,查看显卡显存剩余容量
CUDA可用,共有 1 个GPU设备可用。 当前使用的GPU设备索引:0 当前使用的GPU设备名称:NVIDIA T1000 GPU显存总量:4.00 GB 已使用的GPU显存:0.00 GB 剩余GPU显存:4.00 GB PyTorch版本:1.10.1cu102 …...

React16入门到入土
搭建环境 默认你已经安装好 node.js 安装 react 脚手架 学习的过程中,我们采用React官方出的脚手架工具 create-react-app npm install -g create-react-app如果提示没有权限,win 用户可以管理员打开终端,mac 用户 可以在前面加上 sudo …...
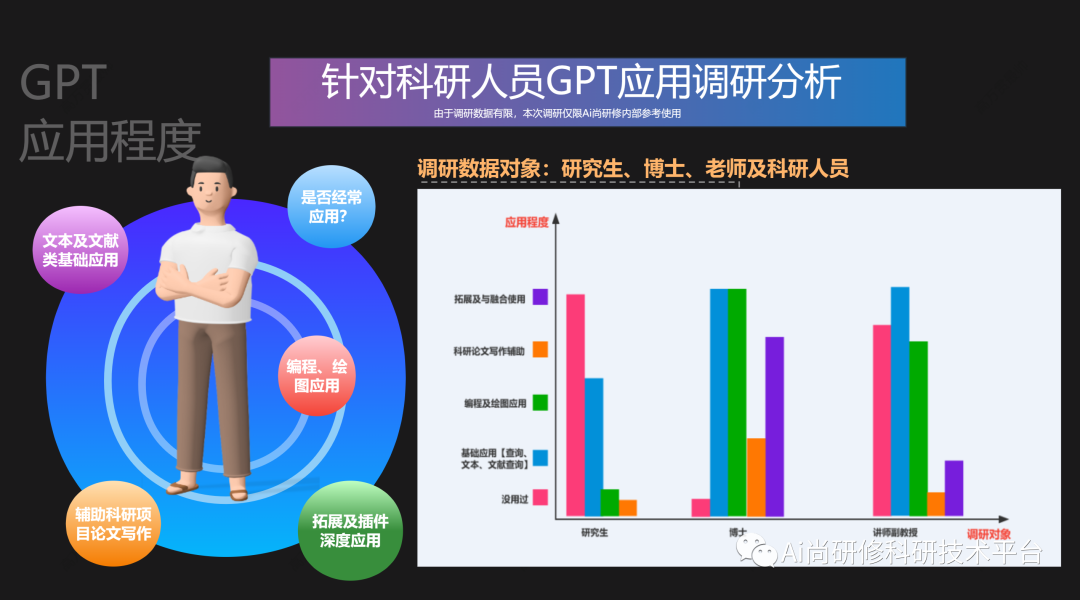
【GPT引领前沿】GPT4技术与AI绘图
推荐阅读: 1、遥感云大数据在灾害、水体与湿地领域典型案例实践及GPT模型应用 2、GPT模型支持下的Python-GEE遥感云大数据分析、管理与可视化技术 GPT对于每个科研人员已经成为不可或缺的辅助工具,不同的研究领域和项目具有不同的需求。例如在科研编程…...

【LeetCode】19. 删除链表的倒数第 N 个结点
19. 删除链表的倒数第 N 个结点(中等) 方法:快慢指针 思路 为了找到倒数第 n 个节点,我们应该先找到最后一个节点,然后从它开始往前数 n-1 个节点就是要删除的节点。 对于一般情况:设置 fast 和 slow 两个…...

spring boot3.x集成swagger出现Type javax.servlet.http.HttpServletRequest not present
1. 问题出现原因 spring boot3.x版本依赖于jakarta依赖包,但是swagger依赖底层应用的javax依赖包,所以只要已启动就会报错。 2. 解决方案 移除swagger2依赖 <dependency><groupId>io.springfox</groupId><artifactId>springfo…...

《低代码指南》——智能化低代码开发实践案例
大模型能通过自然语言理解自动生成需求文档及代码供给低代码开发者使用,也具备自动检测和修复代码错误、自动优化代码、找出冗余并提供高效方案等自动化能力,为开发者带来需求模式、设计模式、开发模式的变化,节省时间成本、代码质量更优、进…...
 + 7) / 8)、字节对齐(((number) + 3) / 4 * 4))
268_C++_字节计算(((bits) + 7) / 8)、字节对齐(((number) + 3) / 4 * 4)
这段代码中包含了两个宏的定义,它们似乎用于进行位操作和字节对齐操作。让我们逐个来解析这两个宏: BITS_TO_BYTES(bits) 宏:#define BITS_TO_BYTES(bits) (((bits) + 7) / 8)这个宏的作用是将位数(bits)转换为字节数(bytes)。它的计算方式是将位数加上7,然后除以8,这…...
JavaWeb知识梳理(后端部分)
JavaWeb 静态web资源(如html 页面):指web页面中供人们浏览的数据始终是不变。 动态web资源:指web页面中供人们浏览的数据是由程序产生的,不同时间点访问web页面看到的内容各不相同。 静态web资源开发技术࿱…...

AI:07-基于卷积神经网络的海洋生物的识别
当涉及海洋生物的识别和研究时,基于深度学习的方法已经展现出了巨大的潜力。深度学习模型可以利用大量的图像和标记数据来自动学习特征,并实现高准确度的分类任务。本文将介绍如何使用深度学习技术来实现海洋生物的自动识别,并提供相应的代码示例。 数据收集和预处理 要训…...

centos7下docker设置新的下载镜像源并调整存放docker下载镜像的仓库位置
目录 1.设置镜像源 2.调整存放下载镜像的仓库位置 1.设置镜像源 在 /etc/docker下创建一个daemon.json文件。在json中下入 "registry-mirrors": ["https://docker.mirrors.ustc.edu.cn/"] 完成配置 加载配置 systemctl daemon-reload 重启docker sy…...

Gitea--私有git服务器搭建详细教程
一.官方文档 https://docs.gitea.com/zh-cn/说明 gitea 是一个自己托管的Git服务程序。他和GitHub, Gitlab等比较类似。他是从 Gogs 发展而来,gitea的创作团队重新fork了代码,并命名为giteagitea 功能特性多,能够满足我们所有的的代码管理需…...

SOLIDWORKS放样是什么意思?
SOLIDWORKS是一款广受欢迎的三维计算机辅助设计(CAD)软件,提供了许多强大的功能来帮助工程师实现他们的创意。其中一个重要的功能是放样功能,它在设计过程中起着至关重要的作用。本文将介绍SOLIDWORKS放样的概念、特点和应用。 放…...
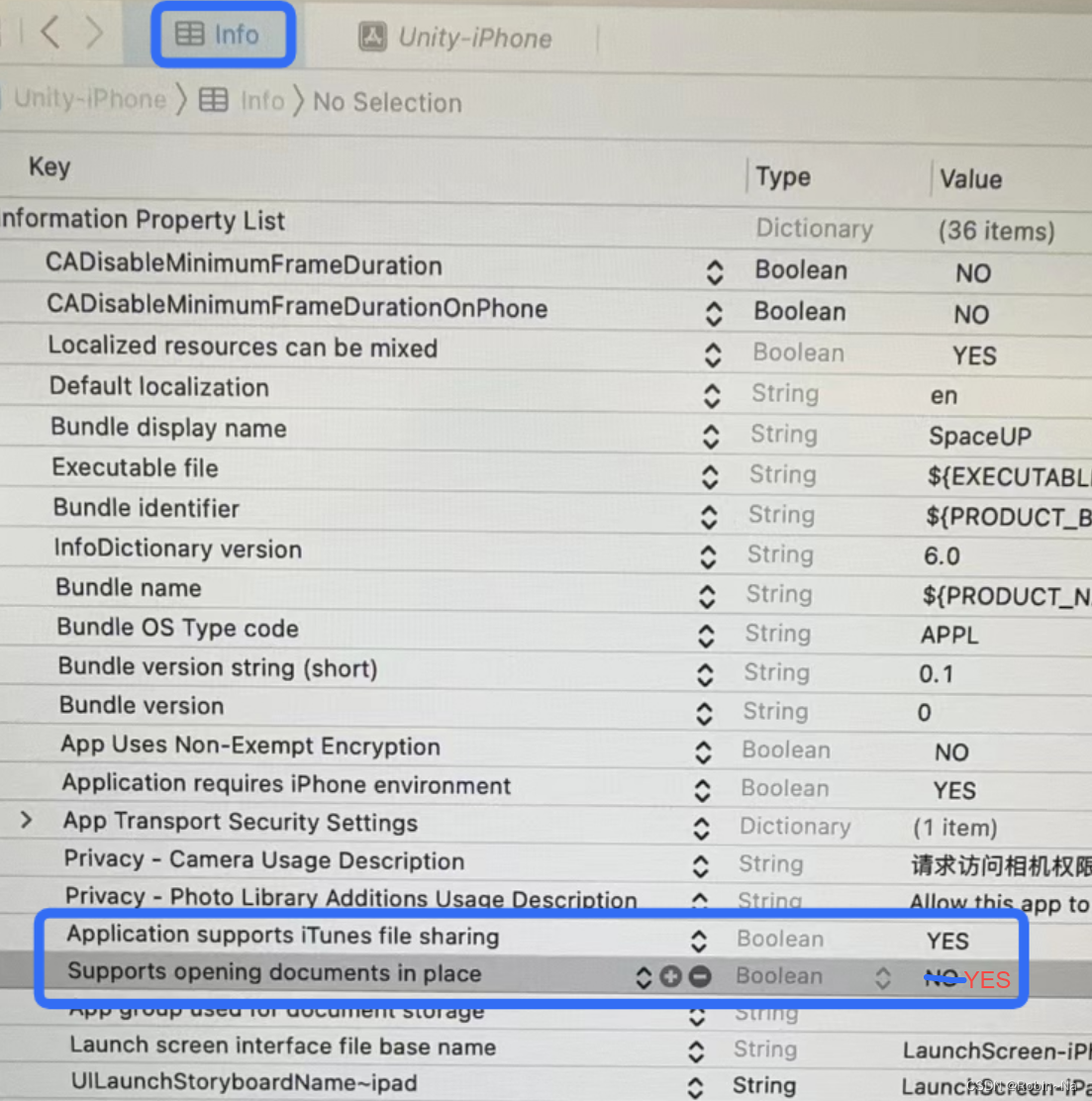
Xcode打包ipa文件,查看app包内文件
1、Xcode发布ipa文件前,在info中打开如下两个选项,即可在手机上查看app包名文件夹下的文件及数据。...
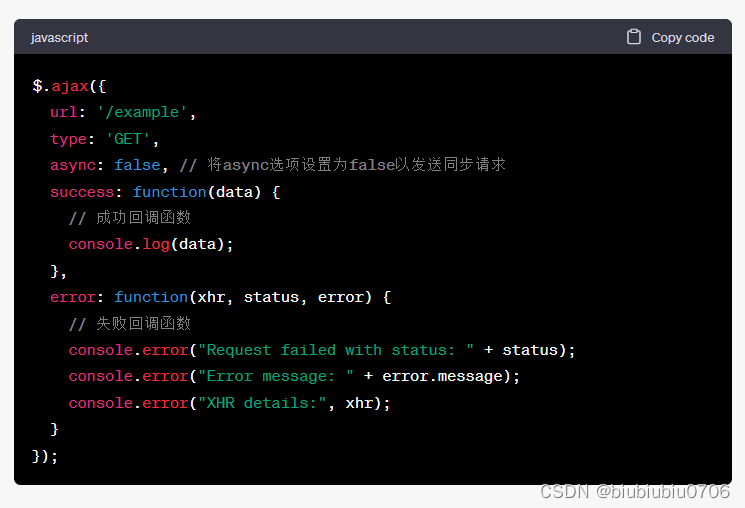
AJAX学习笔记6 JQuery对AJAX进行封装
AJAX学习笔记5同步与异步理解_biubiubiu0706的博客-CSDN博客 AJAX请求相关的代码都是类似的,有很多重复的代码,这些重复的代码能不能不写,能不能封装一个工具类。要发送ajax请求的话,就直接调用这个工具类中的相关函数即可。 用J…...
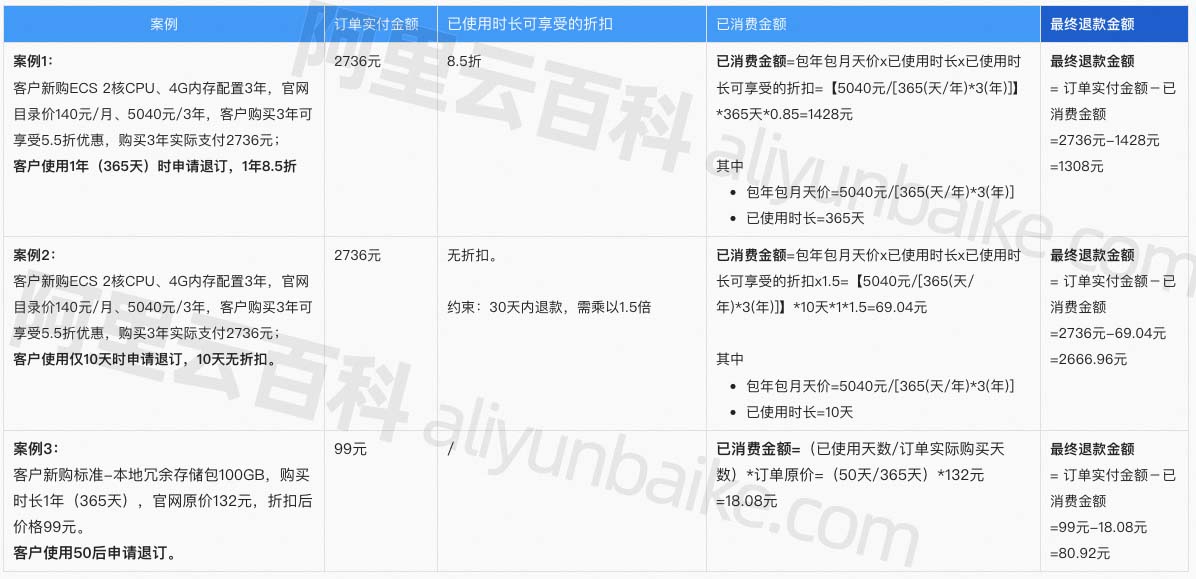
阿里云服务器退款规则_退款政策全解析
阿里云退款政策全解析,阿里云退款分为五天无理由全额退和非全额退订两种,阿里云百科以云服务器为例,阿里云服务器包年包月支持五天无理由全额退订,可申请无理由全额退款,如果是按量付费的云服务器直接释放资源即可。阿…...
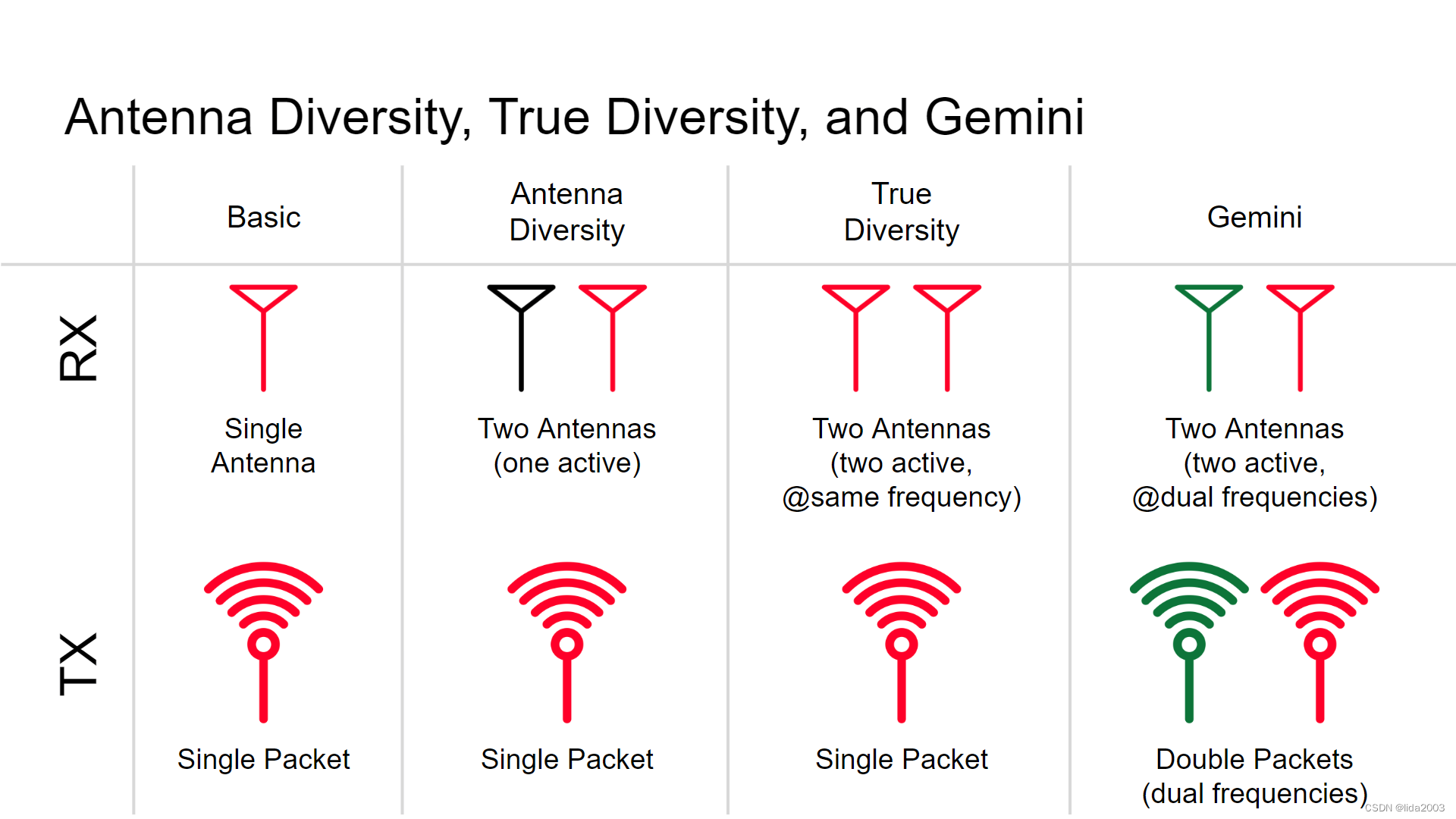
ExpressLRS开源之基本调试数据含义
ExpressLRS开源之基本调试数据含义 1. 源由2. 代码2.1 debugRcvrLinkstats2.2 debugRcvrSignalStats 3. 含义解释3.1 ID(packetCounter),Antenna,RSSI(dBm),LQ,SNR,PWR,FHSS,TimingOffset3.2 IRQ_CNT,RSSI_AVE,SNR_AVE,SNV_MAX,TELEM_CNT,FAIL_CNT 4. 总结5. 参考资料 1. 源由 …...

DOM 简介 | 深入了解DOM
目录 一、DOM是什么 二、DOM的访问 三、DOM节点类型 四、DOM的分级 今天我们将了解WEB编程中一个重要的概念DOM(Document Object Model)文档对象模型,它帮助我们使用JavaScript(或其他编程语言)操纵文档。 一、DO…...
)
机器学习丨2. 线性回归(Linear Regression)
Author:AXYZdong 硕士在读 工科男 有一点思考,有一点想法,有一点理性! 定个小小目标,努力成为习惯!在最美的年华遇见更好的自己! CSDNAXYZdong,CSDN首发,AXYZdong原创 唯…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...
