高精度乘法模板(fft)
正常高精度复杂度是o(n^2),fft复杂度o(nlogn)
#define int long long//__int128 2^127-1(GCC)
#define PII pair<int,int>
#define f first
#define s second
using namespace std;
const int inf = 0x3f3f3f3f3f3f3f3f, N = 3e5 + 5, mod = 1e9 + 7;
const double PI = acos(-1);
int n, m;
struct Complex
{double x, y;Complex operator+ (const Complex& t) const{return { x + t.x, y + t.y };}Complex operator- (const Complex& t) const{return { x - t.x, y - t.y };}Complex operator* (const Complex& t) const{return { x * t.x - y * t.y, x * t.y + y * t.x };}
}a[N], b[N];int rev[N], bit, tot;
void fft(Complex a[], int inv)
{for (int i = 0; i < tot; i++)if (i < rev[i])swap(a[i], a[rev[i]]);for (int mid = 1; mid < tot; mid <<= 1){auto w1 = Complex({ cos(PI / mid), inv * sin(PI / mid) });for (int i = 0; i < tot; i += mid * 2){auto wk = Complex({ 1, 0 });for (int j = 0; j < mid; j++, wk = wk * w1){auto x = a[i + j], y = wk * a[i + j + mid];a[i + j] = x + y, a[i + j + mid] = x - y;}}}
}
signed main() {ios_base::sync_with_stdio(0);cin.tie(0), cout.tie(0);string aa, bb;cin >> aa >> bb;n = aa.size()-1, m = bb.size()-1;for (int i = 0; i <= n; i++) { a[i].x = aa[i] - '0'; }for (int i = 0; i <= m; i++) { b[i].x = bb[i] - '0'; }while ((1 << bit) < n + m + 1) bit++;tot = 1 << bit;for (int i = 0; i < tot; i++) {rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));}fft(a, 1), fft(b, 1);for (int i = 0; i < tot; i++) a[i] = a[i] * b[i];fft(a, -1);string s;int t=0;for (int i = n+m; i >= 0; i--) {t+=(int)(a[i].x / tot + 0.5);s+=t%10+'0';t/=10;}if(t) s+=t+'0';reverse(s.begin(),s.end());cout<<s;
}
相关文章:
)
高精度乘法模板(fft)
正常高精度复杂度是o(n^2),fft复杂度o(nlogn) #define int long long//__int128 2^127-1(GCC) #define PII pair<int,int> #define f first #define s second using namespace std; const int inf 0x3f3f3f3f3f3f3f3f, N 3e5 5, mod 1e9 7; const doubl…...

C# 现状简单说明
文章目录 环境框架图形界面后端游戏 环境 .net framework 老版本.net版本,只能在windows环境下运行 .net core 新版.net版本。可以跨linux,mac平台运行 框架 图形界面 Winfrom 很老的图形界面。特点是丑,但是能用,学起来快 WPF 使用Xaml…...
)
el-table滚动加载、懒加载(自定义指令)
我们在实际工作中会遇到这样的问题: 应客户要求,某一个列表不允许分页。但是不分页的话,如果遇到大量的数据加载,不但后端响应速度变慢,前端的渲染效率也会降低,页面出现明显的卡顿。 那如何解决这个问题…...
不关闭Tamper Protection(篡改保护)下强制卸载Windows Defender和安全中心所有组件
个人博客: xzajyjs.cn 背景介绍 由于微软不再更新arm版本的win10系统,因此只能通过安装insider preview的镜像来使用。而能找到的win10 on arm最新版镜像在安装之后由于内核版本过期,无法打开Windows安全中心面板了,提示如下: 尝…...

从一到无穷大 #13 How does Lindorm TSDB solve the high cardinality problem?
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 本作品 (李兆龙 博文, 由 李兆龙 创作),由 李兆龙 确认,转载请注明版权。 文章目录 引言优势挑战系统架构细节/优化存储引擎索引写入查询 经验Ablation Study总结 引言 …...

三维模型OBJ格式轻量化的纹理压缩和质量关系分析
三维模型OBJ格式轻量化的纹理压缩和质量关系分析 三维模型的OBJ格式通常包含纹理信息,而对纹理进行轻量化压缩可以减小文件大小和提高加载性能。然而,在进行纹理压缩时需要权衡压缩比率和保持质量之间的关系,并根据具体应用场景选择合适的压缩…...

【每日一题】54. 螺旋矩阵
54. 螺旋矩阵 - 力扣(LeetCode) 给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。 示例 1: 输入:matrix [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5…...
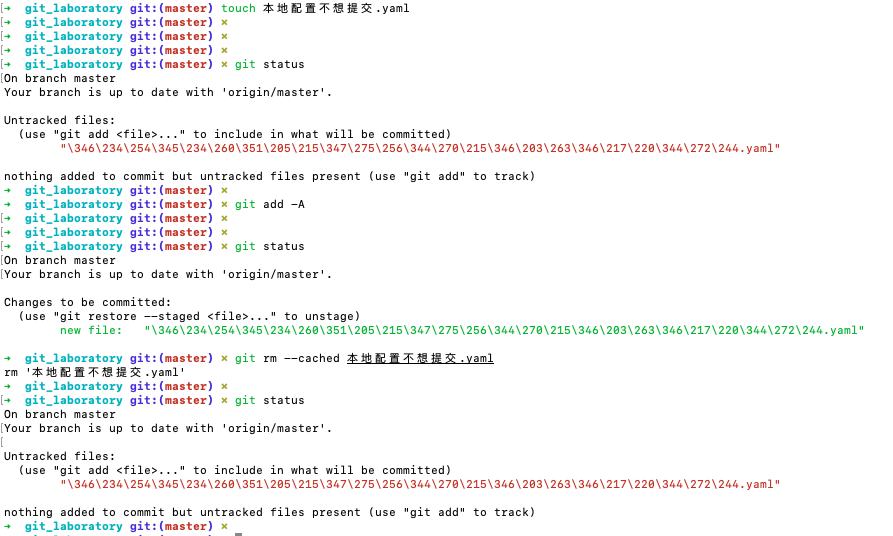
git:一些撤销操作
参考自 如何撤销 Git 操作?[1] 一、撤销提交 git revert HEAD 撤销上次提交. (会在当前提交后面,新增一次提交,抵消掉上一次提交导致的所有变化,所有记录都会保留) 二、撤销某次merge git merge --abort 三、替换上一次提交 git commit --ame…...

leetcode 209. 长度最小的子数组
题目链接:leetcode 209 1.题目 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,…...

《rk3399:各显示接口的dts配置》
这里写目录标题 一、前言二、平台支持的显示接口三、两个VOP支持的最大输出分辨率四、VOPL的dts配置五、VOPB的dts配置六、display_subsystem的配置七、backlight 背光配置八、针对eDP接口的配置 以firefly为例8.1 原生配置8.2 启用eDP屏接口配置九、针对MIPI接口屏的配置 以fi…...

Python数据分析-Pandas
Pandas 个人笔迹,建议不看 import pandas as pd import numpy as npSeries类型 spd.Series([1,3,5,np.nan,6,8],index[a,b,c,d,e]) print(s) # 默认0-n-1,否则用index数组作行标 s.index s.value # array() s[a] &g…...

golang 多线程管理 -- chatGpt
提问: 用golang写一个启动函数 start(n) 和对应的停止函数stopAll(),. start函数功能:启动n个线程,线程循环打印日志,stopAll()函数功能:停止start启动的线程 以下是一个示例的Golang代码,其中包括 start…...

【Math】导数、梯度、雅可比矩阵、黑塞矩阵
导数、梯度、雅可比矩阵、黑塞矩阵都是与求导相关的一些概念,比较容易混淆,本文主要是对它们的使用场景和定义进行区分。 首先需要先明确一些函数的叫法(是否多元,以粗体和非粗体进行区分): 一元函数&…...

【C语言】——调试技巧
目录 编辑 ①前言 1.什么是Bug? 2.什么是调试? 2.1调试的基本步骤 2.2Release与Debug 3.常用快捷键 4.如何写出好的代码 4.1常见的coding技巧 👉assert() 👉const() const修饰指针: ①前言 调试是每个程序员都…...
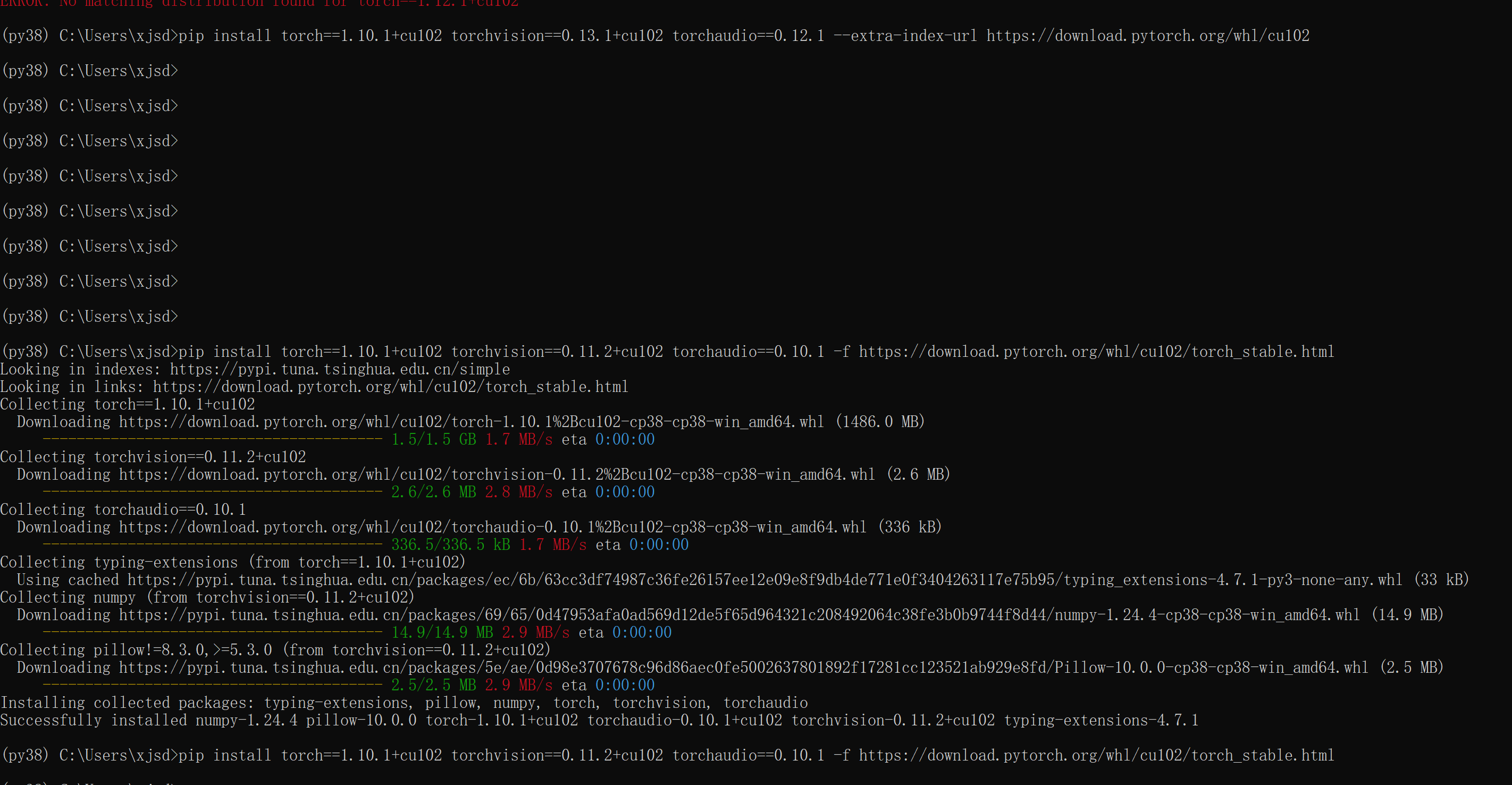
【Python】pytorch,CUDA是否可用,查看显卡显存剩余容量
CUDA可用,共有 1 个GPU设备可用。 当前使用的GPU设备索引:0 当前使用的GPU设备名称:NVIDIA T1000 GPU显存总量:4.00 GB 已使用的GPU显存:0.00 GB 剩余GPU显存:4.00 GB PyTorch版本:1.10.1cu102 …...

React16入门到入土
搭建环境 默认你已经安装好 node.js 安装 react 脚手架 学习的过程中,我们采用React官方出的脚手架工具 create-react-app npm install -g create-react-app如果提示没有权限,win 用户可以管理员打开终端,mac 用户 可以在前面加上 sudo …...
【GPT引领前沿】GPT4技术与AI绘图
推荐阅读: 1、遥感云大数据在灾害、水体与湿地领域典型案例实践及GPT模型应用 2、GPT模型支持下的Python-GEE遥感云大数据分析、管理与可视化技术 GPT对于每个科研人员已经成为不可或缺的辅助工具,不同的研究领域和项目具有不同的需求。例如在科研编程…...

【LeetCode】19. 删除链表的倒数第 N 个结点
19. 删除链表的倒数第 N 个结点(中等) 方法:快慢指针 思路 为了找到倒数第 n 个节点,我们应该先找到最后一个节点,然后从它开始往前数 n-1 个节点就是要删除的节点。 对于一般情况:设置 fast 和 slow 两个…...

spring boot3.x集成swagger出现Type javax.servlet.http.HttpServletRequest not present
1. 问题出现原因 spring boot3.x版本依赖于jakarta依赖包,但是swagger依赖底层应用的javax依赖包,所以只要已启动就会报错。 2. 解决方案 移除swagger2依赖 <dependency><groupId>io.springfox</groupId><artifactId>springfo…...

《低代码指南》——智能化低代码开发实践案例
大模型能通过自然语言理解自动生成需求文档及代码供给低代码开发者使用,也具备自动检测和修复代码错误、自动优化代码、找出冗余并提供高效方案等自动化能力,为开发者带来需求模式、设计模式、开发模式的变化,节省时间成本、代码质量更优、进…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
