Python入门教程 | Python3 集合(Set)
Python3 集合(Set)
集合(set)是一个无序的不重复元素序列。
集合中的元素不会重复,并且可以进行交集、并集、差集等常见的集合操作。
可以使用大括号 { } 创建集合,元素之间用逗号 , 分隔, 或者也可以使用 set() 函数创建集合。
创建格式:
parame = {value01,value02,...}
或者
set(value)
以下是一个简单实例:
set1 = {1, 2, 3, 4} # 直接使用大括号创建集合
set2 = set([4, 5, 6, 7]) # 使用 set() 函数从列表创建集合
注意:创建一个空集合必须用 set() 而不是 { },因为 { } 是用来创建一个空字典。
更多实例演示:
>>> basket = {'apple', 'orange', 'apple', 'pear', 'orange', 'banana'}
>>> print(basket) # 这里演示的是去重功能
{'orange', 'banana', 'pear', 'apple'}
>>> 'orange' in basket # 快速判断元素是否在集合内
True
>>> 'crabgrass' in basket
False>>> # 下面展示两个集合间的运算.
...
>>> a = set('abracadabra')
>>> b = set('alacazam')
>>> a
{'a', 'r', 'b', 'c', 'd'}
>>> a - b # 集合a中包含而集合b中不包含的元素
{'r', 'd', 'b'}
>>> a | b # 集合a或b中包含的所有元素
{'a', 'c', 'r', 'd', 'b', 'm', 'z', 'l'}
>>> a & b # 集合a和b中都包含了的元素
{'a', 'c'}
>>> a ^ b # 不同时包含于a和b的元素
{'r', 'd', 'b', 'm', 'z', 'l'}
类似列表推导式,同样集合支持集合推导式(Set comprehension):
>>> a = {x for x in 'abracadabra' if x not in 'abc'}
>>> a
{'r', 'd'}
集合的基本操作
1、添加元素
语法格式如下:
s.add( x )
将元素 x 添加到集合 s 中,如果元素已存在,则不进行任何操作。
>>> thisset = set(("Google", "Tarzan", "Taobao"))
>>> thisset.add("Facebook")
>>> print(thisset)
{'Taobao', 'Facebook', 'Google', 'Tarzan'}
还有一个方法,也可以添加元素,且参数可以是列表,元组,字典等,语法格式如下:
s.update( x )
x 可以有多个,用逗号分开。
>>> thisset = set(("Google", "Tarzan", "Taobao"))
>>> thisset.update({1,3})
>>> print(thisset)
{1, 3, 'Google', 'Taobao', 'Tarzan'}
>>> thisset.update([1,4],[5,6])
>>> print(thisset)
{1, 3, 4, 5, 6, 'Google', 'Taobao', 'Tarzan'}
>>>
2、移除元素
语法格式如下:
s.remove( x )
将元素 x 从集合 s 中移除,如果元素不存在,则会发生错误。
>>> thisset = set(("Google", "Tarzan", "Taobao"))
>>> thisset.remove("Taobao")
>>> print(thisset)
{'Google', 'Tarzan'}
>>> thisset.remove("Facebook") # 不存在会发生错误
Traceback (most recent call last):File "<stdin>", line 1, in <module>
KeyError: 'Facebook'
>>>
此外还有一个方法也是移除集合中的元素,且如果元素不存在,不会发生错误。格式如下所示:
s.discard( x )
代码实例
>>> thisset = set(("Google", "Tarzan", "Taobao"))
>>> thisset.discard("Facebook") # 不存在不会发生错误
>>> print(thisset)
{'Taobao', 'Google', 'Tarzan'}
我们也可以设置随机删除集合中的一个元素,语法格式如下:
s.pop()
脚本模式实例:
thisset = set(("Google", "Tarzan", "Taobao", "Facebook"))
x = thisset.pop()print("随机删除元素:"+x)
输出结果:
Tarzan
多次执行测试结果都不一样。
set 集合的 pop 方法会对集合进行无序的排列,然后将这个无序排列集合的左面第一个元素进行删除。
3、计算集合元素个数
语法格式如下:
len(s)
交互模式下,计算集合 s 元素个数。
>>> thisset = set(("Google", "Tarzan", "Taobao"))
>>> len(thisset)
3
4、清空集合
语法格式如下:
s.clear()
清空集合 s。
交互模式下实例:
>>> thisset = set(("Google", "Tarzan", "Taobao"))
>>> thisset.clear()
>>> print(thisset)
set()
5、判断元素是否在集合中存在
语法格式如下:
x in s
判断元素 x 是否在集合 s 中,存在返回 True,不存在返回 False。
交互模式下实例:
>>> thisset = set(("Google", "Tarzan", "Taobao"))
>>> "Tarzan" in thisset
True
>>> "Facebook" in thisset
False
>>>
集合内置方法完整列表
| 方法 | 描述 |
|---|---|
| add() | 为集合添加元素 |
| clear() | 移除集合中的所有元素 |
| copy() | 拷贝一个集合 |
| difference() | 返回多个集合的差集 |
| difference_update() | 移除集合中的元素,该元素在指定的集合也存在。 |
| discard() | 删除集合中指定的元素 |
| intersection() | 返回集合的交集 |
| intersection_update() | 返回集合的交集。 |
| isdisjoint() | 判断两个集合是否包含相同的元素,如果没有返回 True,否则返回 False。 |
| issubset() | 判断指定集合是否为该方法参数集合的子集。 |
| issuperset() | 判断该方法的参数集合是否为指定集合的子集 |
| pop() | 随机移除元素 |
| remove() | 移除指定元素 |
| symmetric_difference() | 返回两个集合中不重复的元素集合。 |
| symmetric_difference_update() | 移除当前集合中在另外一个指定集合相同的元素,并将另外一个指定集合中不同的元素插入到当前集合中。 |
| union() | 返回两个集合的并集 |
| update() | 给集合添加元素 |
相关文章:
)
Python入门教程 | Python3 集合(Set)
Python3 集合(Set) 集合(set)是一个无序的不重复元素序列。 集合中的元素不会重复,并且可以进行交集、并集、差集等常见的集合操作。 可以使用大括号 { } 创建集合,元素之间用逗号 , 分隔, 或…...
视频汇聚/视频云存储/视频监控管理平台EasyCVR安全检查的相关问题及解决方法2.0
开源EasyDarwin视频监控TSINGSEE青犀视频平台EasyCVR能在复杂的网络环境中,将分散的各类视频资源进行统一汇聚、整合、集中管理,在视频监控播放上,TSINGSEE青犀视频安防监控汇聚平台可支持1、4、9、16个画面窗口播放,可同时播放多…...

【C++模拟实现】反向迭代器的实现
【C模拟实现】反向迭代器的实现 目录 【C模拟实现】反向迭代器的实现反向迭代器的代码示例反向迭代器的模拟实现要点引入iterator模版参数rbegin()和rend()的实现 作者:爱写代码的刚子 时间:2023.9.5 前言:本篇博客主要介绍反向迭代器的实现&…...

Kubernetes技术--k8s核心技术持久化存储
有时候需要在集群中进行一些重要的数据进行持久化存储,然后需要的时候再进行挂载,那么下面我们一起来看看如何实现数据的持久化存储操作。 1.nfs网络存储 -1.找一台服务器做nfs的服务端,安装nfs。(这里我们直接在master上实现)。 这里应该找再单独的搭建一个node节点做持…...
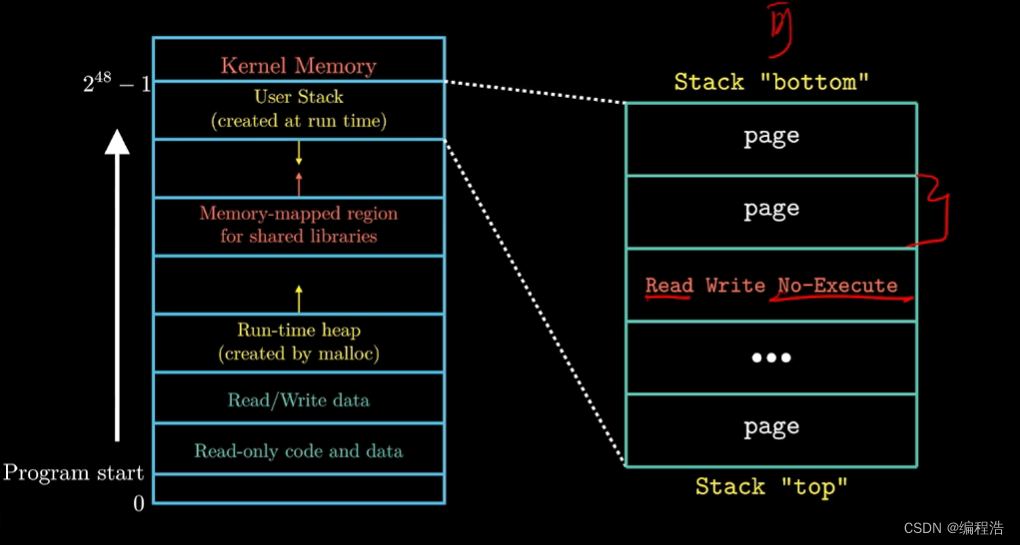
【80天学习完《深入理解计算机系统》】第十四天 复习第三章
专注 效率 记忆 预习 笔记 复习 做题 欢迎观看我的博客,如有问题交流,欢迎评论区留言,一定尽快回复!(大家可以去看我的专栏,是所有文章的目录) 文章字体风格: 红色文字表示&#…...

库中是如何实现string类的?
🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨ 🐻推荐专栏1: 🍔🍟🌯C语言初阶 🐻推荐专栏2: 🍔🍟🌯C语言进阶 🔑个人信条: 🌵知行合一 …...

无涯教程-JavaScript - WORKDAY.INTL函数
描述 WORKDAY.INTL函数返回带有自定义周末参数的指定工作日数之前或之后的日期的序列号。周末参数指示哪些和多少天是周末。周末和指定为假期的任何日子均不视为工作日。 语法 WORKDAY.INTL (start_date, days, [weekend], [holidays])争论 Argument描述Required/OptionalS…...

STM32--蓝牙
本文主要介绍基于STM32F103C8T6和蓝牙模块实现的交互控制 简介 蓝牙(Bluetooth)是一种用于无线通信的技术标准,允许设备在短距离内进行数据交换和通信。它是由爱立信(Ericsson)公司在1994年推出的,以取代…...

java 实现原型模式
原型模式(Prototype Pattern)是一种创建型设计模式,它允许创建对象的副本,而无需暴露对象的创建细节。在Java中,原型模式通常通过克隆对象来实现。要实现原型模式,需要满足以下条件: 被克隆的对…...
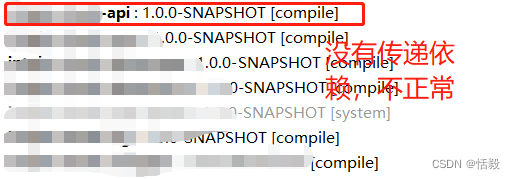
maven本地安装jar包install-file,解决没有pom的问题
背景: 公司因为权限问题,没有所有的代码,内部maven还在搭建,所以需要拿到同事的jar包,本地install: mvn install:install-file -DgroupIdcom..framework -DartifactIdcloud-api -Dversion1.0.0-SNAPSHOT …...
【C++学习笔记】5、变量作用域
文章目录 【 1、局部变量 】【 2、全局变量 】【 3、局部变量和全局变量的初始化 】 作用域是程序的一个区域,一般来说有三个地方可以定义变量: 在函数或一个代码块内部声明的变量,称为局部变量。 在函数参数的定义中声明的变量,称…...
Python中的装饰器
迷途小书童的 Note 读完需要 5分钟 速读仅需 2 分钟 装饰器是一个非常有用而又常被误解的功能,可以让我们在不修改函数或类的源代码情况下给它们提供扩展功能。本文将通过具体示例带你深入理解 Python 装饰器的用法。 1 装饰器基础 装饰器本质上是一个函数ÿ…...
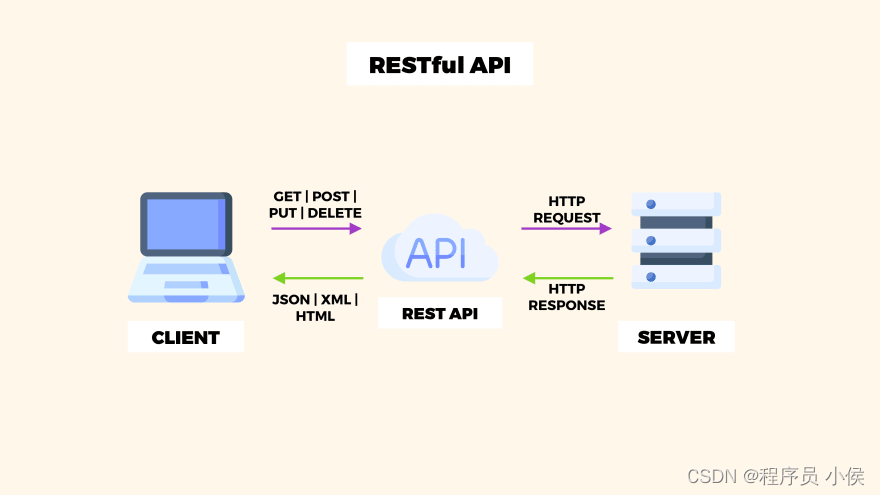
什么是RESTful API,Spring MVC如何支持RESTful架构
文章目录 🎈个人主页:程序员 小侯 🎐CSDN新晋作者 🎉欢迎 👍点赞✍评论⭐收藏 ✨收录专栏:Java框架 ✨文章内容:Spring MVC支持RESTful架构 🤝希望作者的文章能对你有所帮助…...

cin、cin.getline()、getline()的用法【C++】
一、cin>> 用法1:输入一个数字或字符 #include <iostream> using namespace std; int main () {int a,b;cin>>a>>b;cout<<ab<<endl;return 0; } 用法2:接收一个字符串,遇“空格”、“TAB”、“回车”…...
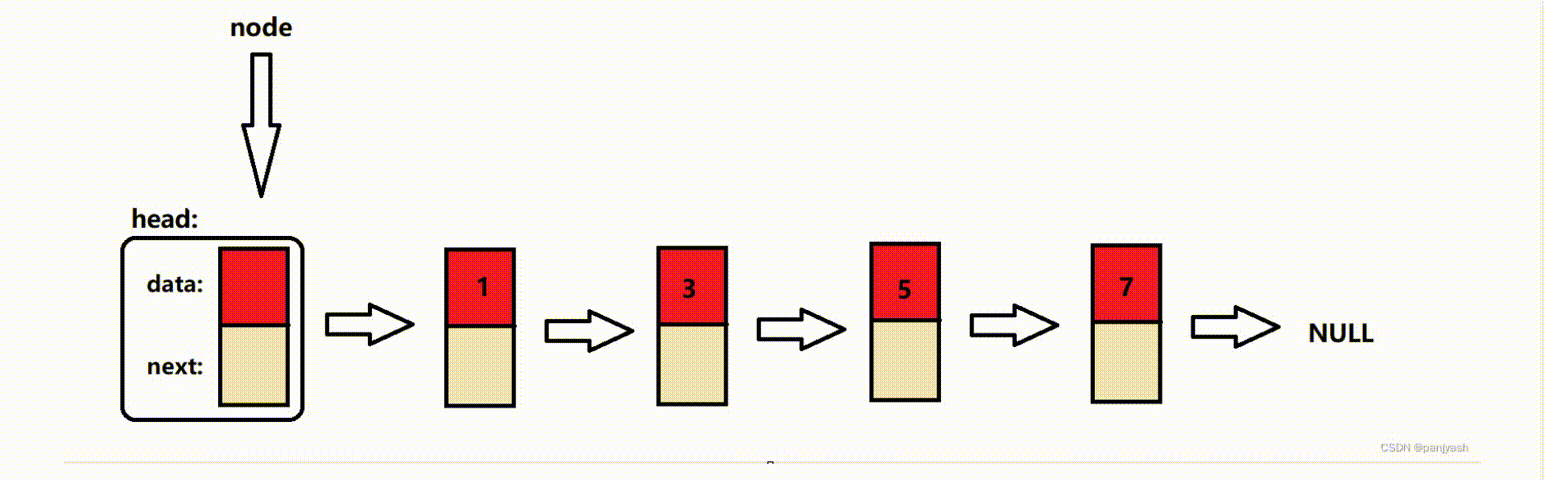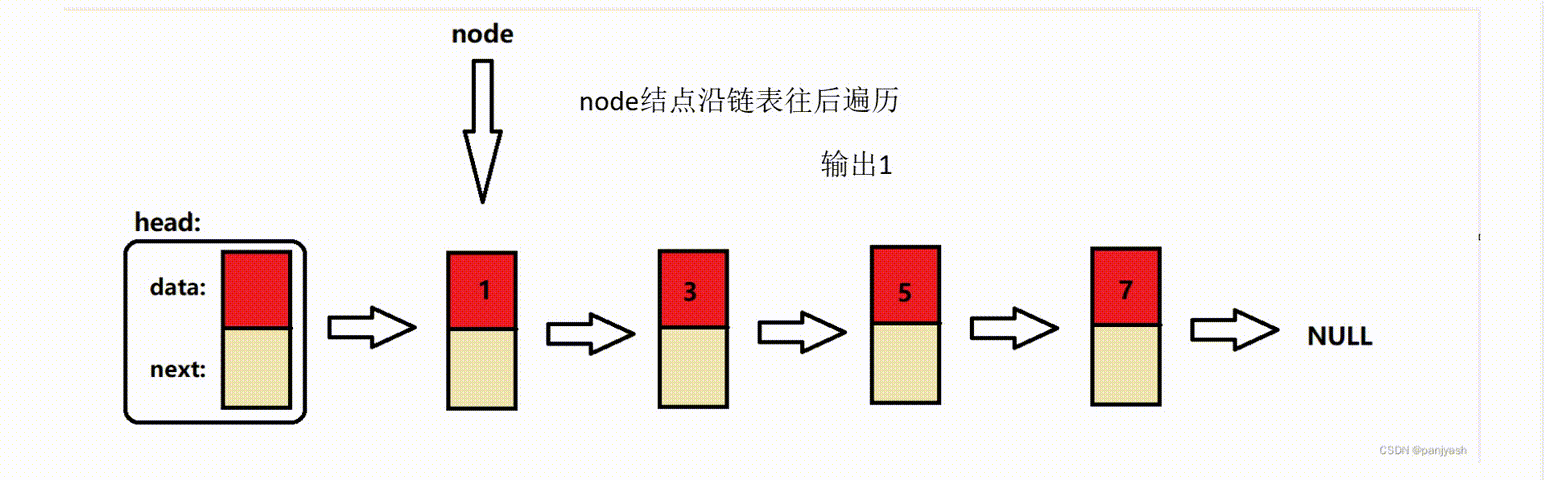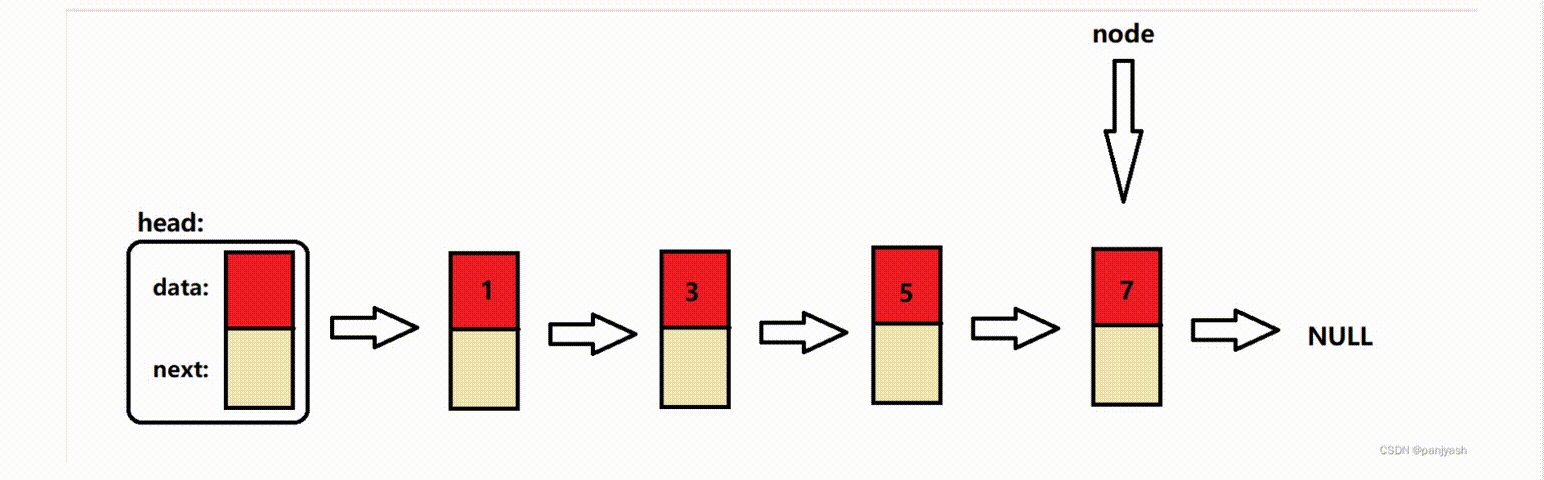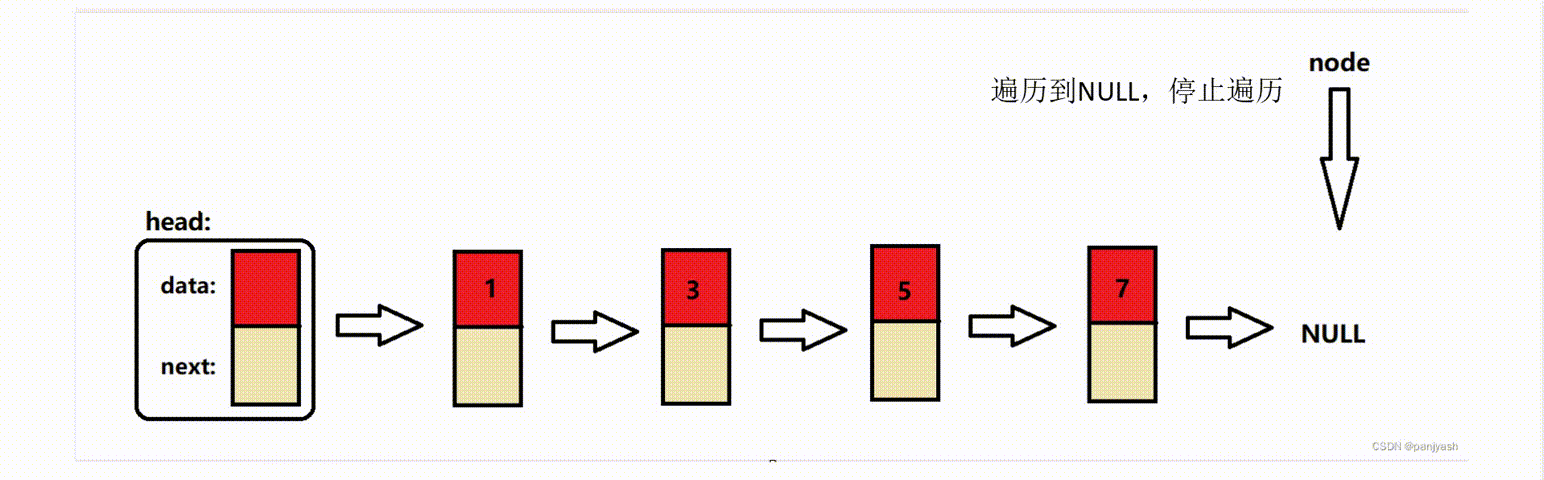
单向链表(c/c++)
链表是一种常见的数据结构,其中运用到了结构体指针,链表可以实现动态存储分配,换而言之,链表是一个功能强大的数组,可以在某个节点定义多种数据类型,可以实现任意的添加,删除,插入节…...
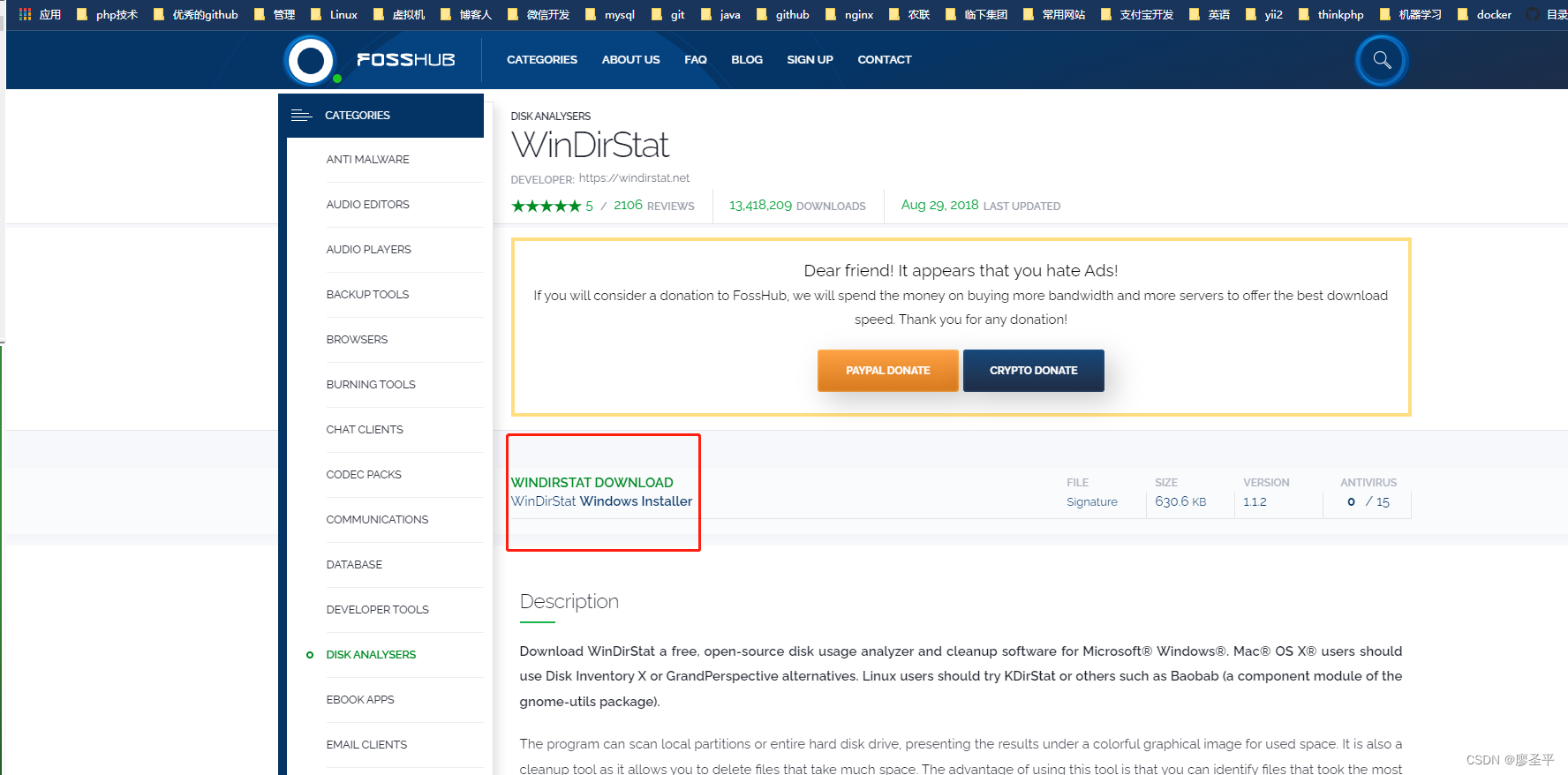
像linux 一样清理Windows C盘
像 linux 有命令 du -sh 查看文件夹大小 但是windows 可就没有这个命令了,就算有命令,也不能扫描子目录里面的文件 但是windows 可以借助 软件来清理,和linux 一样 文件上面是目录,下面是文件所占用空间大小的图,咋…...

在Linux 下制作启动盘以及dd命令使用
在Linux 下制作启动盘以及dd命令使用 1、在Linux 下制作启动盘,可使用如下命令:2、Linux dd 命令(1)参数说明: 3、dd应用实例(1)将本地的/dev/hdb整盘备份到/dev/hdd(2)将/dev/hdb全盘数据备份到指定路径的image文件(3)将备份文件恢复到指定盘(4)备份/de…...

C语言插入排序
前言: 本文主要讲解插入排序中的直接插入排序和希尔排序。 1、直接插入排序: 1.1基本思想 直接插入排序是一种简单的插入排序法,其基本思想是把待排序的数值按照大小顺序逐个插入到一个已经排好序的有序序列中,直到将所有记录…...

SQL-DCL
DCL-管理用户 1.查询用户 USE mysql; SELECT * FROM user; 2.创建用户 CREATE USER “用户名”“主机名” IDENTIFIED BY "密码“; 3.修改用户密码 ALTER USER “用户名”“主机名” IDENTIFIED WITH mysql_native_password BY &quo…...
Elasticsearch 中的向量搜索:设计背后的基本原理
作者:ADRIEN GRAND 实现向量数据库有不同的方法,它们有不同的权衡。 在本博客中,你将详细了解如何将向量搜索集成到 Elastisearch 中以及我们所做的权衡。 你有兴趣了解 Elasticsearch 用于向量搜索的特性以及设计是什么样子吗? …...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
