C语言插入排序

前言：

本文主要讲解插入排序中的直接插入排序和希尔排序。

1、直接插入排序：

1.1基本思想

直接插入排序是一种简单的插入排序法，其基本思想是把待排序的数值按照大小顺序逐个插入到一个已经排好序的有序序列中，直到将所有记录插入完为止，得到一个新的有序序列。

实际中我们玩扑克牌时，就用了插入排序的思想。

下面的图片就是插入排序的整体过程，第一步认为5是一个有序区间，然后2比5小，就让5向后移，前面填充2，又形成一个有序的序列，以此类推……

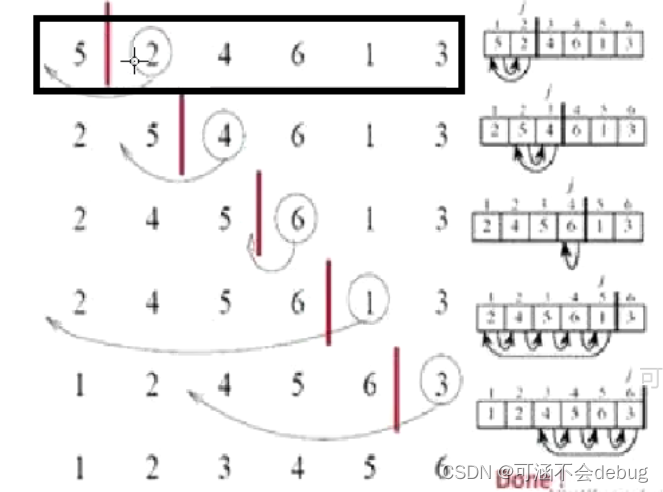
原码：

外层的循环相当于每次插入的扑克牌，内层循环决定了这张扑克牌怎么插，插在哪里

void StraightInsert(int arr[], int n)
{//[0-end]有序，插入end+1位置的数，使得[0-end+1]序列仍然有序for (int i = 0;i<n-1;i++){int end = i;int tmp = arr[i + 1];while (end >= 0){if (arr[end] > tmp){arr[end + 1] = arr[end];end--;}elsebreak;}arr[end + 1] = tmp;}
}

时间复杂度：

时间复杂度计算的是完成程序的次数，不能只看是双层循环就 武断 O(N^2)！

前面讲过时间复杂度计算的是最差的情况，最差的情况就是将逆序的排成升序的，1+2+3+……n-1，这是一共累加的次数，求和发现这是一个等差数列求和，最高项就是N^2，因此时间复杂度就是O(N^2)。

最好的情况下本来就是顺序，end位置的值都需要跟前面一个比较，所以就是O(N)。

2、希尔排序

2.1概念：

希尔排序是一种特殊的直接插入排序，也算是直接插入排序的优化版本。

2.2思想：

我们发现在一些直接插入排序的例子时，发现其实一些排序是很接近O(N)。

比如1，2，5，3，6

因此我们想先进行预排序（让原来的排序更接近有序），接着再进行直接插入排序。

2.3预排序

何为预排序？

预排序就是分组排，间隔为gap的为一组，注意 组数==gap的值

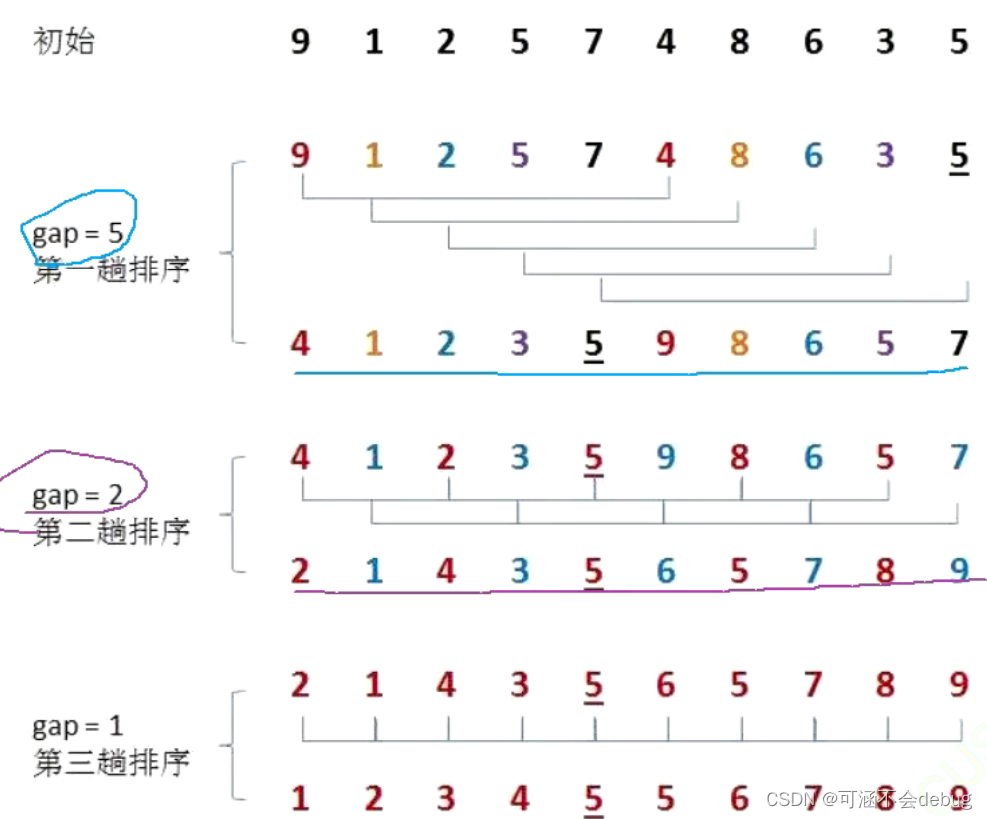
预排序的规律：（重要）

• 多组间隔为gap的预排序，gap从大到小
• gap越大：大的数可以越快的到后面，小的数可以越快的到前面。
• gap越大，预排序越不接近有序
• gap越小，预排序越接近有序
• gap==1时，就是直接插入排序。

那gap到底是多少呢？

这个问题较难回答，这个问题没有官方的答案。

首先gap不可能是一个固定的数，应该与数组的长度n相关，我们一般采用gap ==  n/ 2的表达式来去定义gap的值，因为要保证最后gap要被除到1为止

原码：

void ShellSort(int arr[], int n)
{int gap = n;while (gap > 1){gap = gap / 3+1;for (int i = 0; i < n - gap; i++)//这里的循环判断条件也很有讲究，正好能将多组gap排完{int end = i;int tmp = arr[end + gap];while (end >= 0){if (tmp < arr[end]){arr[end + gap] = arr[end];//将数据往后移end -= gap;}elsebreak;}arr[end + gap] = tmp;}}
}

通过代码，我们不难发现预排序大部分的代码内容与直接插入排序是一样的，只不过将1换成了gap而已。

预排序需要排很多次，真的比直接插入排序快嘛？

我们自己可以比较这两种排序方式上的时间差距，经过比较我们发现，直接插入排序的时间要比希尔排序的时间多上100倍左右！（随着N的增大，时间差也会增大）

时间复杂度

首先外层的while循环执行的次数是logN，内层的循环当gap很大时，执行次数是N，当gap很小时，执行次数也接近于N，所以最终的时间复杂度O(logN*N)。

注意N^2与N*logN两者并不是一个量级的，特别是当N的数非常大时。

一些书上直接给出了结论O(N^1.3)。