040、动态规划基本技巧(labuladong)
动态规划基本技巧
一、动态规划解题套路框架
基于labuladong的算法网站,动态规划解题套路框架;
1、基本介绍
基本套路框架:
- 动态规划问题的一般形式是求最值;
- 核心如下:
- 穷举;
- 明确base case;
- 明确状态和状态转移,什么选择导致状态如何变化’
- 定义dp数组,存储的值是什么
代码框架:
# 自顶向下递归的动态规划
def dp(状态1, 状态2, ...):for 选择 in 所有可能的选择:# 此时的状态已经因为做了选择而改变result = 求最值(result, dp(状态1, 状态2, ...))return result# 自底向上迭代的动态规划
# 初始化 base case
dp[0][0][...] = base case
# 进行状态转移
for 状态1 in 状态1的所有取值:for 状态2 in 状态2的所有取值:for ...dp[状态1][状态2][...] = 求最值(选择1,选择2...)2、斐波那契数列
力扣第509题,斐波那契数;
[509]斐波那契数//leetcode submit region begin(Prohibit modification and deletion)
class Solution {public int fib(int n) {// 判断 nif (n <= 1) {return n;}return dp(n);}// 动态规划int dp(int n) {int[] memo = new int[n + 1];// base casememo[0] = 0;memo[1] = 1;for (int i = 2; i <= n; i++) {memo[i] = memo[i - 1] + memo[i - 2];}return memo[n];}
}
//leetcode submit region end(Prohibit modification and deletion)3、凑零钱问题
力扣第322题,零钱兑换;
[322]零钱兑换//leetcode submit region begin(Prohibit modification and deletion)
class Solution {/*** @param coins:不同面额的硬币数组* @param amount:需要凑满的总金额* @return 返回利用不同面额的硬币数组,凑满总金额时,最少的硬币个数*/public int coinChange(int[] coins, int amount) {// 利用一个备忘录数组memo = new int[amount + 1];// 将备忘录中填充值Arrays.fill(memo, -666);return find(coins, amount);}int[] memo;// 所需硬币个数int find(int[] coins, int amount) {// base caseif (amount == 0) {return 0;}if (amount < 0) {return -1;}// 防止重复计算if (memo[amount] != -666) {return memo[amount];}// 遍历 coins 数组int res = Integer.MAX_VALUE;for (int coin : coins) {// 如果此时选择 coin 这枚硬币,可以将问题分解成子问题int subRes = find(coins, amount - coin);// 比较结果if (subRes == -1) {continue;// 该情况无解}res = Math.min(res, subRes + 1);}// 将结果存入备忘录memo[amount] = res == Integer.MAX_VALUE ? -1 : res;return memo[amount];}
}
//leetcode submit region end(Prohibit modification and deletion)二、动态规划设计:最长递增子序列
基于labuladong的算法网站,动态规划设计:最长递增子序列;
1、最长递增子序列
力扣第300题,最长递增子序列;
[300]最长递增子序列//leetcode submit region begin(Prohibit modification and deletion)
class Solution {public int lengthOfLIS(int[] nums) {// 利用一个备忘录int length = nums.length;// memo[i]:为i位置为结尾的最长严格递增子序列的长度int[] memo = new int[length];// 数组初始化Arrays.fill(memo, 1);int res = 0;// 开始遍历for (int i = 0; i < length; i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) {memo[i] = Math.max(memo[i], 1 + memo[j]);}}}// 找到最大的for (int i = 0; i < length; i++) {if (memo[i] > res) {res = memo[i];}}return res;}
}
//leetcode submit region end(Prohibit modification and deletion)2、俄罗斯套娃信封问题
力扣第354题,俄罗斯套娃信封问题;
[354]俄罗斯套娃信封问题//leetcode submit region begin(Prohibit modification and deletion)
class Solution {// envelopes = [[w, h], [w, h]...]public int maxEnvelopes(int[][] envelopes) {int n = envelopes.length;// 按宽度升序排列,如果宽度一样,则按高度降序排列Arrays.sort(envelopes, new Comparator<int[]>(){public int compare(int[] a, int[] b) {return a[0] == b[0] ?b[1] - a[1] : a[0] - b[0];}});// 对高度数组寻找 LISint[] height = new int[n];for (int i = 0; i < n; i++)height[i] = envelopes[i][1];return lengthOfLIS(height);}public int lengthOfLIS(int[] nums) {// 利用一个备忘录int length = nums.length;// memo[i]:为i位置为结尾的最长严格递增子序列的长度int[] memo = new int[length];// 数组初始化Arrays.fill(memo, 1);int res = 0;// 开始遍历for (int i = 0; i < length; i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) {memo[i] = Math.max(memo[i], 1 + memo[j]);}}}// 找到最大的for (int i = 0; i < length; i++) {if (memo[i] > res) {res = memo[i];}}return res;}
}
//leetcode submit region end(Prohibit modification and deletion)三、最优子结构原理和 DP 数组遍历方向
基于labuladong的算法网站,最优子结构原理和 DP 数组遍历方向;
1、最优子结构
动态规划问题一般都是求最值问题,本质是重叠的子问题,从base case开始去往后推导,整个过程就是状态转移正确的过程;
2、如何一眼看出重叠子问题
最简单直接的办法是画出递归图,如果有重叠的子问题,就需要引入备忘录;
3、dp数组
- dp数组大小其实是根据自己的base case定义,设置出来的;
- dp数组的遍历方向是自己根据状态转移过程设计的,可以正向遍历,也可以反向遍历;
- 只需要保证遍历之前,最优子结构的答案已经解出;
- 遍历之后,该位置的答案被解出;
四、BASE CASE 和备忘录的初始值怎么定?
基于labuladong的算法网站,BASE CASE 和备忘录的初始值怎么定?;
力扣第931题,下降路径最小和;
[931]下降路径最小和//leetcode submit region begin(Prohibit modification and deletion)
class Solution {public int minFallingPathSum(int[][] matrix) {int length = matrix.length;memo = new int[length][length];// memo 初始化for (int i = 0; i < length; i++) {Arrays.fill(memo[i], Integer.MAX_VALUE);}// 找到最小值int res = Integer.MAX_VALUE;for (int j = 0; j < length; j++) {res = Math.min(res, dp(matrix, length - 1, j));}return res;}// 定义一个备忘录int[][] memo;// memo[i][j] 代表从第一行中的任何元素开始,到达i,j位置的下降路径最小和/*** @param matrix:整数数组* @param i:第i行* @param j:第j列* @return 从整数数组中第一行的仍和元素开始,达到第i行第j列的元素的下降路径最小和*/int dp(int[][] matrix, int i, int j) {// 判断是否越界if (i < 0 || j < 0 || i >= matrix.length || j >= matrix.length) {return Integer.MAX_VALUE;}// base caseif (i == 0) {// 如果是第一行的元素,那么就等于其本身return matrix[0][j];}// 判断 memo 中是否已经算出该位置的结果if (memo[i][j] != Integer.MAX_VALUE) {return memo[i][j];}// 否则开始算,进行状态转移memo[i][j] = matrix[i][j] + min(dp(matrix, i - 1, j), dp(matrix, i - 1, j - 1), dp(matrix, i - 1, j + 1));return memo[i][j];}int min(int a, int b, int c) {return Math.min(a, Math.min(b, c));}
}
//leetcode submit region end(Prohibit modification and deletion)相关文章:
)
040、动态规划基本技巧(labuladong)
动态规划基本技巧 一、动态规划解题套路框架 基于labuladong的算法网站,动态规划解题套路框架; 1、基本介绍 基本套路框架: 动态规划问题的一般形式是求最值;核心如下: 穷举;明确base case;…...

html笔记(一)
一、html简介 什么是HTML? Hyper Text Markup Language 超文本标记语言 超文本?超级文本,例如流媒体,声音、视频、图片等。 标记语言?这种语言是由大量的标签组成。 任何一个标签都有开始标签和结束标签&…...

索引的情况
select * from A left join B on A.c B.c where A.employee_id 3 1.一句sql中 是可能走多次索引的,具体的 一般 表连接 ,或者说生成临时表的时候,会走索引 然后条件过滤的时候也会走索引,具体的 还是要具体分析 2.表连接 字段…...
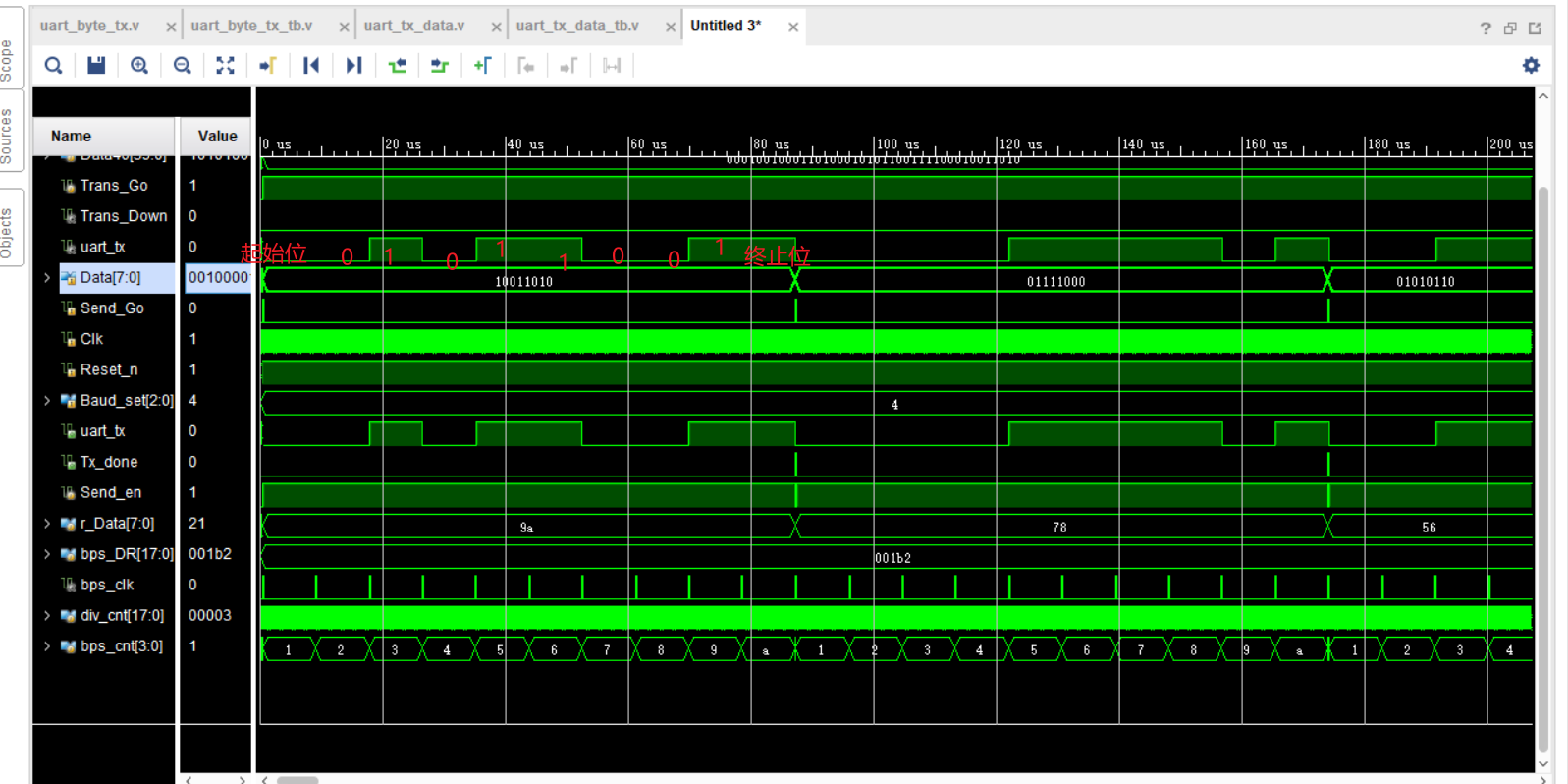
Verilog 学习第五节(串口发送部分)
小梅哥串口部分学习part1 串口通信发送原理串口通信发送的Verilog设计与调试串口发送应用之发送数据串口发送应用之采用状态机实现多字节数据发送串口通信发送原理 1:串口通信模块设计的目的是用来发送数据的,因此需要有一个数据输入端口 2:…...

破解遗留系统快速重构的5步心法(附实例)
前两天和一个架构师朋友闲聊,说到了 「重构」 这个话题,他们公司早年间上线的项目系统,因一直没专人在演进过程中为代码质量负责,导致现在代码越来越混乱,逐渐堆积成“屎山”,目前的维护成本已远高于重新开…...
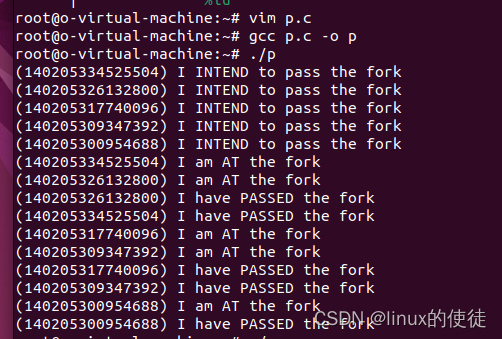
信号量(上)实验
实验1:解决订票终端的临界区管理 订票终端是解决冲突问题,所以信号量的值是1 #include <stdio.h> #include <pthread.h> #include <unistd.h> #include <semaphore.h> int ticketAmout 2; // 票的数量: 全局变量 sem_t mutex…...
阿里5年,一个女工对软件测试的理解
成为一个优秀的测试工程师需要具备哪些知识和经验? 针对这个问题,可以直接拆分以下三个小问题来详细说明: 1、优秀软件测试工程师的标准是什么? 2、一个合格的测试工程师需要具备哪些专业知识? 3、一个合格的测试工程…...

前端练习项目
30 Web Projects 30 多个带有 HTML、CSS 和 JavaScript 的 Web 项目,由 Packt Publishing 提供 https://github.com/PacktPublishing/30-Web-Projects-with-HTML-CSS-and-JavaScript Small projects https://github.com/WebDevVikramChoudhary/small_projects_for_…...

sql复习(set运算符、高级子查询)
一、set运算符 union:得到两个查询结果的并集,并且⾃动去掉重复⾏。不会排序 union all:得到两个查询结果的并集,不会去掉重复⾏。也不会排序 intersect:得到两个查询结果的交集,并且按照结果集的第⼀个列进…...

整车电源的几种模式:OFF/ACC/RUN/CRANK
本文框架1.前言2. 四种电源模式2.1 OFF模式2.2 ACC模式2.3 ON模式2.4 CRANK模式3. KL15/KL301.前言 在诊断或者网络管理相关模块开发对客户的需求进行梳理时,经常会看到客户对不同车辆模式下处理策略的需求,如果前期没接触过这几种模式,可能…...

踩了大坑:wordpress后台 无法将上传的文件移动至wp-content
一、问题描述 今天迁移了wordpress站点至新服务器,结果上传图片出现“无法将上传的文件移动至wp-content/uploads”的提示,这是怎么回事,为什么会这样。 报错如下: 2023/02/20 08:57:48 [error] 9861#9861: *79624 FastCGI sen…...

page cache设计及实现
你好,我是安然无虞。 page cache的设计及实现 page cache 本质上也是一个哈希桶, 它是按照页的数量进行映射的. 当 central cache 向 page cache 申请内存时, page cache 先检查对应位置是否有span, 如果没有则向更大页去寻找一个span, 如果找到则分裂成两个. 比如…...
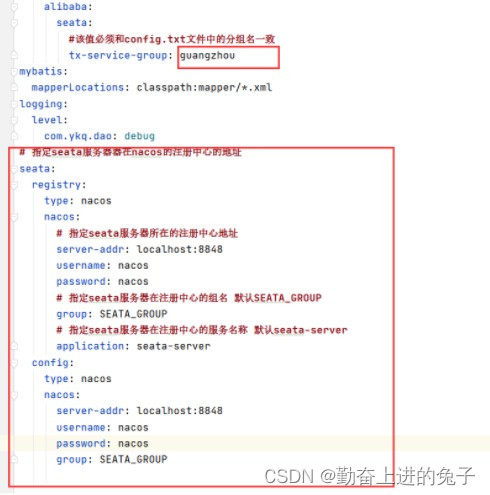
使用seata来解决分布式事务
文章目录 目录 文章目录 前言 一、Seata的执行流程如下 二、使用步骤 三、配置微服务客户端 总结 前言 Seata部署指南 Seata 是一款开源的分布式事务解决方案,致力于提供高性能和简单易用的分布式事务服务。Seata 将为用户提供了 AT、TCC、SAGA 和 XA 事务模…...

推荐一款新的自动化测试框架:DrissionPage
今天给大家推荐一款基于Python的网页自动化工具:DrissionPage。这款工具既能控制浏览器,也能收发数据包,甚至能把两者合而为一,简单来说:集合了WEB浏览器自动化的便利性和 requests 的高效率。 一、DrissionPage产生背…...

MQ系列面试
先来说说什么是MQ,MQ与多线程之间的区别MQ是消息中间件 可以实现异步 多线程也可以实现异步使用传统http协议方式调用接口存在的缺点如果服务器端没有及时的响应给客户端的时候,容易造成客户端阻塞等待。服务器响应超时 客户端发送重试机制 需要考虑避免…...

一句话设计模式2:原型模式
原型模式:每次得到一个新对象。 文章目录 原型模式:每次得到一个新对象。前言一、原型模式和new的区别二、如何实现原型模式1. 什么clone接口2. 开始使用,并验证浅clone效果3. 深度clone(也就是address也要复制一份)总结前言 原型模式可以说是目前接触的设计模式中,比较无用的…...

c++11特性与c++17特性
1、自动类型推导auto // C11 auto func1() -> int // 需要指定返回值类型 {return 10; }auto func2() -> std::function<void()> {auto lambda []() { };return lambda; }// c17 // 之后无需指定返回值类型 auto func1() {return 10; }auto func2() {auto lambda…...
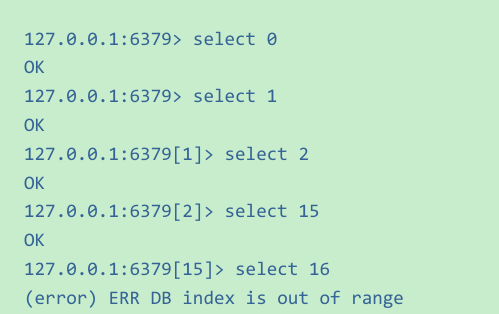
Redis02: Redis基础命令
一、基础命令 先启动redis服务,使用redis-cli客户端连到redis数据库里面 1. 获取符合规则的键: keys 要点: (1)keys 后面可以指定正则表达式 (2)在生产环境下建议禁用keys命令,因为这个命令会查…...

MDK的HardFault硬件异常和NMI异常原因总结
发出来,出现问题自行比对,现在一些代码,也会对这个进行分析。硬件异常原因: Unaligned load or store Load 或者 store 指令访问未对齐地址 Undefined Instruction 执行 ARM 未定义的指令 EPSR Fault 当前程序没有在 Thumb 状态下…...

视频图像质量诊断
视频图像质量诊断有哪些原理,视频图像质量诊断有哪些算法? 视频图像质量诊断技术支持对视频黑屏、视频干扰、视频卡顿、视频遮挡、亮度异常、图像偏色、视频模糊、视频冻结、视频抖动、场景变更、无字符叠加等20种视频图像质量异常进行诊断,…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...
