FSK解调技术的FPGA实现
本原创文章由深圳市小眼睛科技有限公司创作,版权归本公司所有,如需转载,需授权并注明出处
一、FSK信号的解调原理
FSK信号的解调也有非相干和相干两种,FSK信号可以看作是用两个频率源交替传输得到的,所以FSK的接收机由两个并联的ASK接收机组成。
(1)相干解调
相干解调是利用乘法器,输入一路与载频相干的参考信号与载频相乘,通过低通滤波,滤除高频信号,即得原始信号,FSK经过带通滤波之后,可以看作是两路ASK信号,相干检测器组成的原理如下所示:
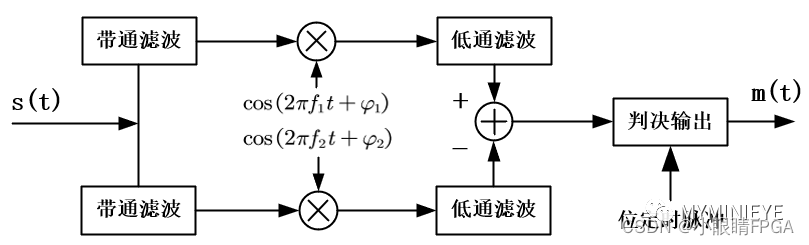
FSK相干解调结构
上图是一种易于实现的FSK相干解调器,还有一种最佳FSK相干解调器如下所示:

FSK最佳解调结构
从图上可以看出,在接收端要产生两个已知信号s1(t)和s2(t)的波形,分别和输入波形相乘,再送往积分器,在一定时间内积分,在t=Tb时刻,将积分结果取样,并在比较器中比较判决,然后输出,整个相干解调器的性能受载波锁相环路以及位同步性能影响很大,并且在高速率的情况下,积分、取样和清洗电路难以实现,因此通常采用第一种相干解调器的结构。
(2)非相干解调
由于FSK信号中提取相干载波相对比较困难,实际工程应用中多用非相干解调法,在相同误码率的条件下,非相干解调需要的信噪比只比相干解调高1~2dB。非相干解调的种类有很多,例如:基于自适应滤波的解调法、差分检波算法、AFC环解调法、过零检测法、包络检波法等。
• 基于自适应滤波的解调法
在自适应解调中,较常见的方法是利用自适应滤波器中的单一频率的自适应陷波器进行解调,它能提供易于控制的带宽和及其深的零点,具有自适应地跟踪载波的频率和相位的能力,它等效于有一个复权的自适应滤波器,用两个实权同时调整单一频率正弦波的幅度和相位,以跟踪原始输入信号的幅度和相位,消除干扰。如下是自适应滤波器的结构:
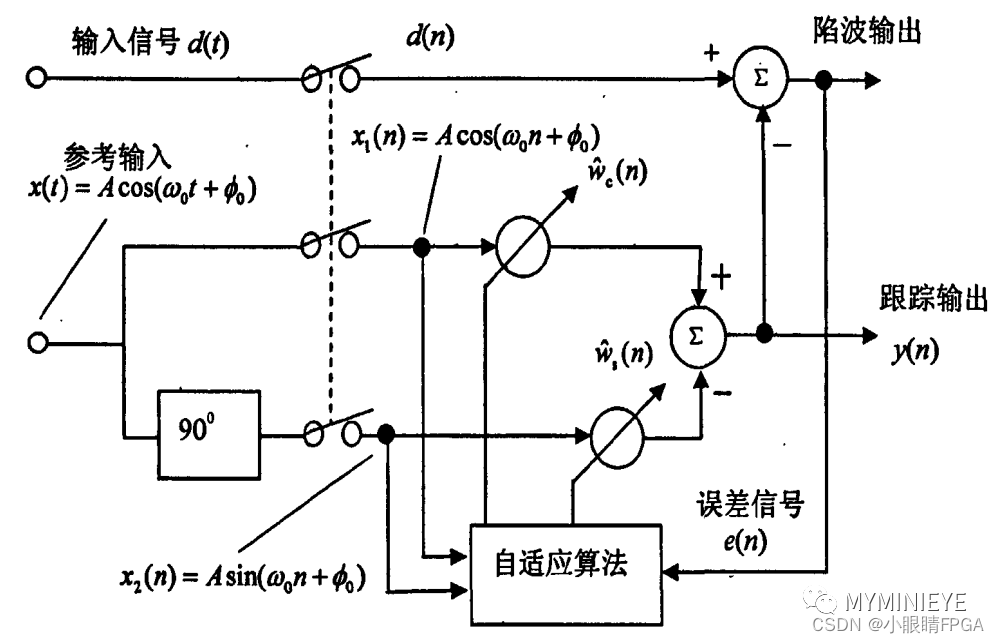
自适应滤波结构
自适应滤波中的单频跟踪技术应用于解调时,兼有解调和锁相的功能,选取适当的步长可以达到较小的传输延迟,并获得优良的解调性能。二进制FSK信号有两个调制频率,能量主要集中在这两个频率。分别采用两个自适应滤波(SFT)跟踪这两个频率的信号,即可将键控频率分量提取出来。然后经过中值滤波提取包络、积分清洗、抽样判决即可还原基带信号。比最佳非相干解调拥有更好的误码性能,特别适合低速率数据场合,解调系统示意图如下:

自适应解调FSK原理
• 差分检波算法
差分检波法解调FSK的原理如下所示:

差分检波法解调原理
设带通滤波器的输出为:

其中We为载波频率,w是角频率偏移,为初始相位,则乘法器的输出为:

用低通滤波器滤除倍频分量,可以得到
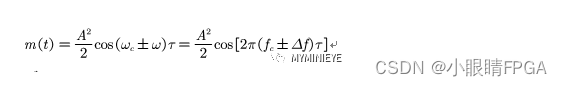
如果令,则
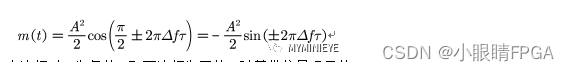
当FSK取上边频时,为负值,取下边频为正值,随基带信号码元的不同,低通滤波输出正负变化的正弦波,通过抽样判决,即可实现FSK信号的解调。这种方法结构上相 对简单,计算量小,便于实现。
• AFC环解调法
AFC环是一个负反馈系统,如果接收信号与本振存在频差,则在一定时间内必然存在相差,鉴相器输出的相位误差信号微分后,得到反映频差的误差信号,经过平滑处理, 控制VCO的震荡频率向输入信号频率靠近最终使得频差近似为零。应用比较广泛的是相乘微分型AFC环路,结构如下所示:
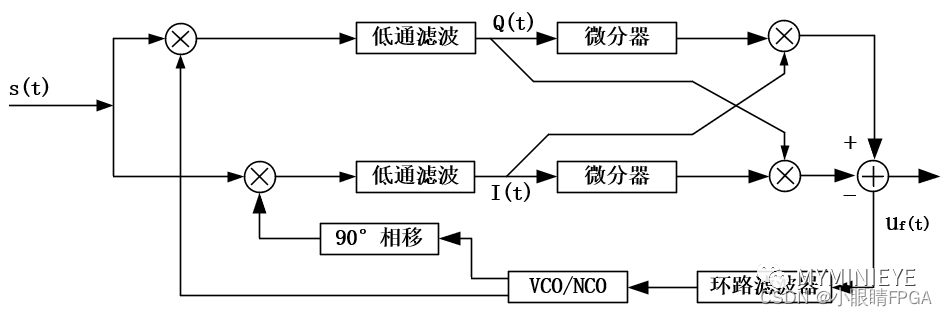
相乘微分型解调原理
设输入信号为:

VCO输入信号为:

由上图可知:
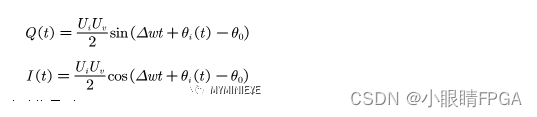
输入信号为单载波信号时:
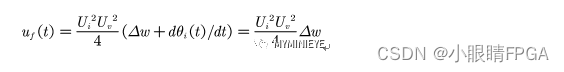
因此 反映了输入信号和VCO输出信号的频差,对FSK信号来讲,
反映了输入信号和VCO输出信号的频差,对FSK信号来讲,  即为调制信号,对其进行滤波判决,即可完成FSK信号的解调。AFC环是根据信号的瞬时频 率来解调数据的,当FSK调制度较小时,区分调制数据越困难,解调性能也越差。
即为调制信号,对其进行滤波判决,即可完成FSK信号的解调。AFC环是根据信号的瞬时频 率来解调数据的,当FSK调制度较小时,区分调制数据越困难,解调性能也越差。
• 过零检测法
过零检测法是一种常用且简便的解调方法,2FSK信号的过零点数随载频的变化而 不同,因此检测出过零点个数就可以得到载频的差异,从而进一步得到调制信号的信息,过零检测法的原理如下:
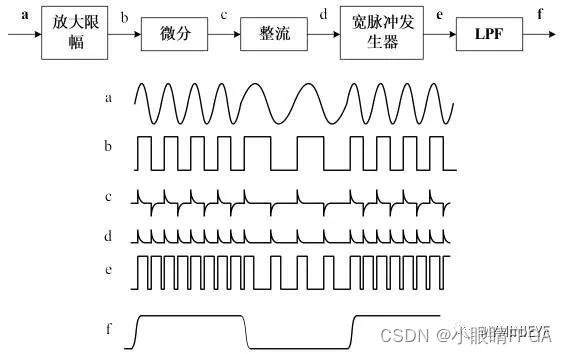
过零检测法解调原理
FSK信号经过限幅、微分、整流后形成与频率变化相对应的脉冲序列,由此再形成 相同宽度的矩形脉冲,矩形脉冲的低频分量与数字信号相对应,由滤波器滤出低频分量, 然后经抽样判决,即可得到原始的数字调制信号。
• 包络检波法
2FSK的包络检波法解调原理如下,可视为由两路2ASK解调电路组成,这里两个带通滤波器,对应两个中心频率,用以分开两路2ASK信号,将两路滤波之后的包络信号相减,在经过抽样判决其进行判决,根据调制规则(f1代表符号1,f2代表符号0),当判决值大于0时,判决为1,否则判决为0。
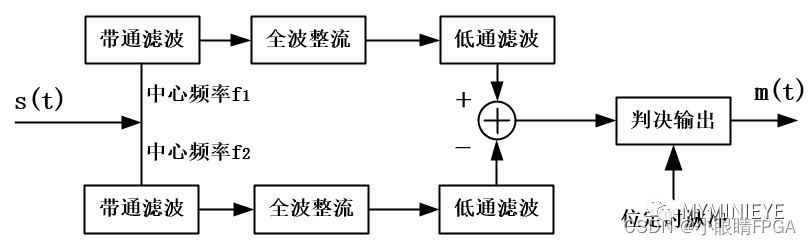
包络检波法解调原理
包络检波首先需要通过带通滤波器将FSK信号进行滤波分离,显然,当调制度较小的时候,两路FSK信号频谱混叠严重,带通滤波器的通带比较窄,能量损失比较严重,会引入另一路信号的频谱干扰,因此性能下降严重,通常需要调制度大于2的时候才能获得较好测性能。
二、FSK解调技术的matlab仿真
这里采用AFC环来实现FSK的解调,之所以选择AFC环是因为AFC环是基于锁相环路的解调技术,且环路增益计算相对简单,可以初步学习锁相环的相关知识。AFC环中有3个滤波器,其中两个正交之路的低通滤波完全相同,用于滤除前级混频后的高频分量;环路滤波器用于滤除鉴频器输出产生的高频分量,产生NCO的控制信号。为了简化设计,环路滤波器也设计成FIR低通滤波器,这样可以直接从环路滤波器的输出信号中获取解调数据,环路滤波器的带宽,过渡带可以和混频器的低通滤波器保持一致。
FSK调制信号的参数如下,其中码元速率为4MHz,采样频率为32MHz,载波频率为70MHz,调制指数为0.715。码元为随机产生的数据,需要写入本地,作为后续比对的数据。

通过fskmod函数产生调制信号,然后将基带信号变频到70MHz的中频,叠加一定的信道噪声,再使用抗混叠滤波器滤除带外频率,防止输入信号的最大频率与采样频率冲突。

然后把数据写入文本作为FPGA解调的输入数据。

设计低通滤波器,滤波器通带及过渡带的选择有一个基本的原则,就是确保有用信号完全通过,尽可能多地对噪声及干扰进行滤除。低通滤波器的通带必须大于捕获带宽,捕获带宽也就是锁相环路起始的频差,为确保不损失有用信号信息,这里选择3.6MHz。
理论上讲,截止频率越靠近通带频率越好,但是过渡带越窄,滤波器的阶数就越多,所需的硬件资源也越多。过渡带带宽的选择原则有两个:一是必须确保滤除相邻的A/D镜像频率成分;二是需要滤除数字下变频引入的倍频分量。根据带通采样定理,A/D镜像频率的最小间隔为:
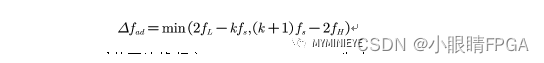
式中fL为中频信号的下边缘频率(70-3.6=66.4MHz),fH为中频信号的上边缘频率(70+3.6=73.6MHz),fs为采样频率(32MHz),k为整数,易求得
数字下变频引入的倍频分量最低频率为:
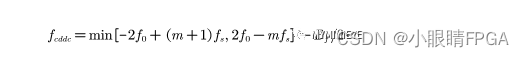
式中,f0为中频采样后的载波频率(6MHz),也可以在频谱中看到,Bf为中频信号处理带宽(7.2MHz),m为整数,易求得fcddc = 8.4MHz。
滤波器的设计如下:

三、FSK解调技术的FPGA实现
AFC环中滤波器设计可以直接导入matlab参数,但是采用FPGA进行数学意义上的微分运算时分困难,根据微分运算的规则,我们可以采用一种简单的近似处理方法,即通过求取前后两个数据之差来代替微分运算,前后两个数据间隔为一个时钟周期
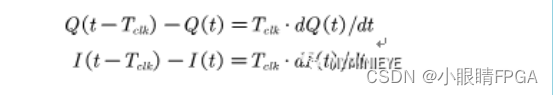
采用前后两个数据之差来代替微分运算,相当于数学上的微分运算乘以时钟速率这个常数,反映在AFC环路上,相当于环路增益乘了一个常数。NCO的参数设计比较简单,区董事中频率选择系统时钟即可,为32MHz,频率字位宽选取30bit,数据位宽为8bit,NCO频率分辨率为
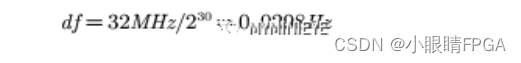
环路锁定的条件是环路增益K必须大于固有频差,且环路增益越大,捕获及锁定时间越短。对2FSK信号,可以设置本地NCO的初始频率为载波频率fc,固有频差即为FSK信号的频偏值,当调制指数为0.715时,码元速率为4MHz,

因此环路能够稳定跟踪FSK信号的变化,解调出原始数据。
1.DDS参数如下,其他的选择默认:

2.Multiplier需要用两个,一个是8*8bit的,数据和DDS位宽都是8位的,取低15位作为有效输出数据。另一个是18*18的,考虑到FPGA中集成硬件乘法器IP核大多多事18*18bit的,DSP48E1是18*25,如果超过18位就需要用两个DSP了,占用更多资源,因此在微分之后取高18位做乘法运算,采用有符号乘法器即可。
3.低通滤波器导入matlab产生的系数,参数设置如下,其他的选择默认:

4.环路滤波器和低通滤波器导入相同的参数,输入数据的位宽可以根据自己截位的舍取进行选择,这里使用的17位,即微分之后,取高17位作为有效数据,然后输入环路滤波器。
编写测试文件,环路滤波器输出的数据即为FSK解调信号,然后通过抽样判决,位同步时钟提取,即可得到二进制码元,把解调的数据写入到本地,用于数据比对。
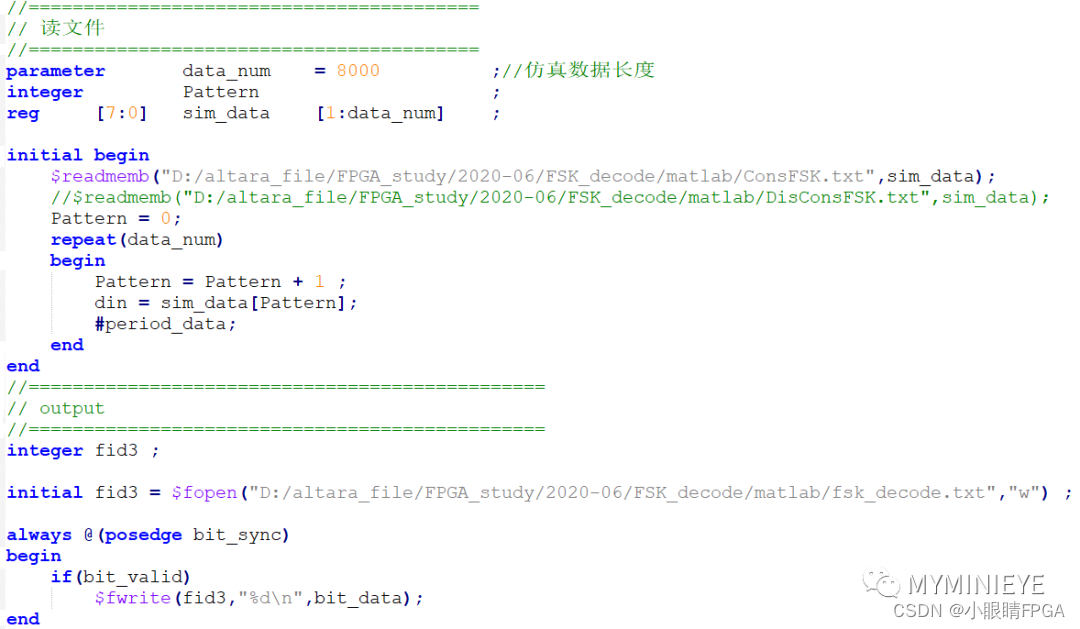
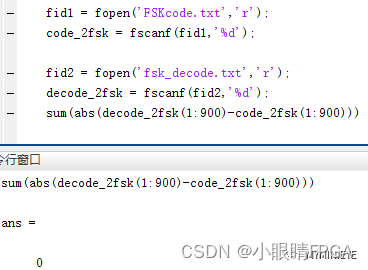
编写完测试激励之后,通过ModelSim仿真结果如下:

得到解调信号,然后通过Matlab和调制信号做比对,结果是一致,验证了解调的正确性
相关文章:

FSK解调技术的FPGA实现
本原创文章由深圳市小眼睛科技有限公司创作,版权归本公司所有,如需转载,需授权并注明出处 一、FSK信号的解调原理 FSK信号的解调也有非相干和相干两种,FSK信号可以看作是用两个频率源交替传输得到的,所以FSK的接收机由…...
Matlab图像处理-高斯低通滤波器
高通滤波 图像的边缘、细节主要位于高频部分,而图像的模糊是由于高频成分比较弱产生的。高通滤波就是为了高消除模糊,突出边缘。因此采用高通滤波器让高频成分通过,消除低频噪声成分削弱,再经傅里叶逆变换得到边缘锐化的图像。 …...
文件上传之图片马混淆绕过与条件竞争
一、图片马混淆绕过 1.上传gif imagecreatefromxxxx函数把图片内容打散,,但是不会影响图片正常显示 $is_upload false; $msg null; if (isset($_POST[submit])){// 获得上传文件的基本信息,文件名,类型,大小&…...

代码随想录二刷day16
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣104. 二叉树的最大深度二、力扣559. N 叉树的最大深度三、力扣111. 二叉树的最小深度三、力扣力扣222. 完全二叉树的节点个数 前言 一、力扣104. 二叉树…...

【开发】安防监控/视频存储/视频汇聚平台EasyCVR优化播放体验的小tips
视频云存储/安防监控EasyCVR视频汇聚平台基于云边端智能协同,可实现视频监控直播、视频轮播、视频录像、云存储、回放与检索、智能告警、服务器集群、语音对讲、云台控制、电子地图、H.265自动转码H.264、平台级联等。为了便于用户二次开发、调用与集成,…...
算法_C++—— 只出现一次的数字)
力扣(LeetCode)算法_C++—— 只出现一次的数字
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。 你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。 示例 1 : 输入࿱…...
Windows配置SonarQube代码审查工具详细步骤(附带IDEA SonarLint插件使用)
文章目录 环境说明以及准备一. SonarQube的下载与安装二. 添加SonarQube项目三. 使用Maven命令上传代码到SonarQube四. IDEA安装SonarLint插件 环境说明以及准备 本篇博客使用的SonarQube版本为9.8,注意JDK 1.8已经不能支持 NameVersionDownLoad LinkSonarQube9.8…...

【Unity3D】UI Toolkit元素
1 前言 UI Toolkit简介 中介绍了 UI Builder、样式属性、UQuery、Debugger,UI Toolkit容器 中介绍了 VisualElement、ScrollView、ListView、GroupBox 等容器,UI Toolkit样式选择器 中介绍了简单选择器、复杂选择器、伪类选择器等样式选择器,…...
Task :app:compileDebugKotlin FAILED
gradle.properties 里面加上 android.enableJetifiertrue...

Android——数据存储(一)(二十一)
1. 数据存储 1.1 知识点 (1)掌握Android数据存储的分类; (2)可以使用SharedPreferences存储数据。 1.2 具体内容 对于我们数据的存储而言,Android一共提供了5个数据存储的方式:SharedPrefe…...

机器学习课后习题 ---数学基础回顾
(一)选择题 1.函数y=1/(x+1)是 A.偶函数 B.奇函数 C.单调函数 D.无界函数 2.设f(sin(x/2)=cosx+1,则f(x)为() A.2x-2 B.2-2x C.1+2 …...
CS420 课程笔记 P4 - 以16进制形态编辑游戏文件
文章目录 IntroductionFinding save filesStringsUnicodeExample!Value searchHealth searchConclusion Introduction 这节课我们将学习编辑十六进制,主要用于编辑保存文件,但十六进制编辑涉及的技能可以很好地转移到: Save file editingRe…...
计算机毕设之Python的高校成绩分析(含文档+源码+部署)
本系统阐述的是一个高校成绩分析系统的设计与实现,对于Python、B/S结构、MySql进行了较为深入的学习与应用。主要针对系统的设计,描述,实现和分析与测试方面来表明开发的过程。开发中使用了 django框架和MySql数据库技术搭建系统的整体架构。…...
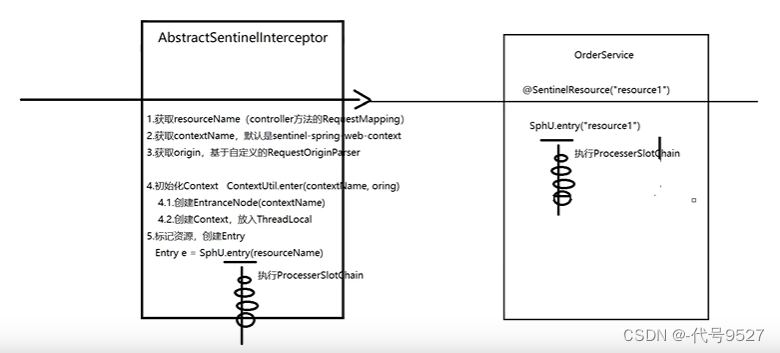
【Sentinel】核心API-Entry与Context
文章目录 一、Entry1、Entry的声明2、使用API自定义资源3、基于SentinelResource注解标记资源 二、Context1、Context介绍2、Context的初始化3、AbstractSentinelInterceptor4、ContextUtil 一、Entry 1、Entry的声明 默认情况下,Sentinel会将controller中的方法作…...

HashMap源码阅读解惑
HashMap的hash函数(1.8) 首先1.7的是四次扰动,1.8做了优化。 简单的说就是对key做hashCode操作,然后将得到的32为散列值向右位移16位,再与hashCode做异或计算。实质上是把一个数的低16位与他的高16位做异或运算。 st…...

如何解决前端传递数据给后端时精度丢失问题
解决精度丢失 有时候我们在进行修改操作时,发现修改既不报错也不生效。我们进行排查后发现服务器端将数据返回给前端时没有出错,但是前端js将数据进行处理时却出错了,因为id是Long类型的,而js在处理后端返回给前端的Long类型数据…...
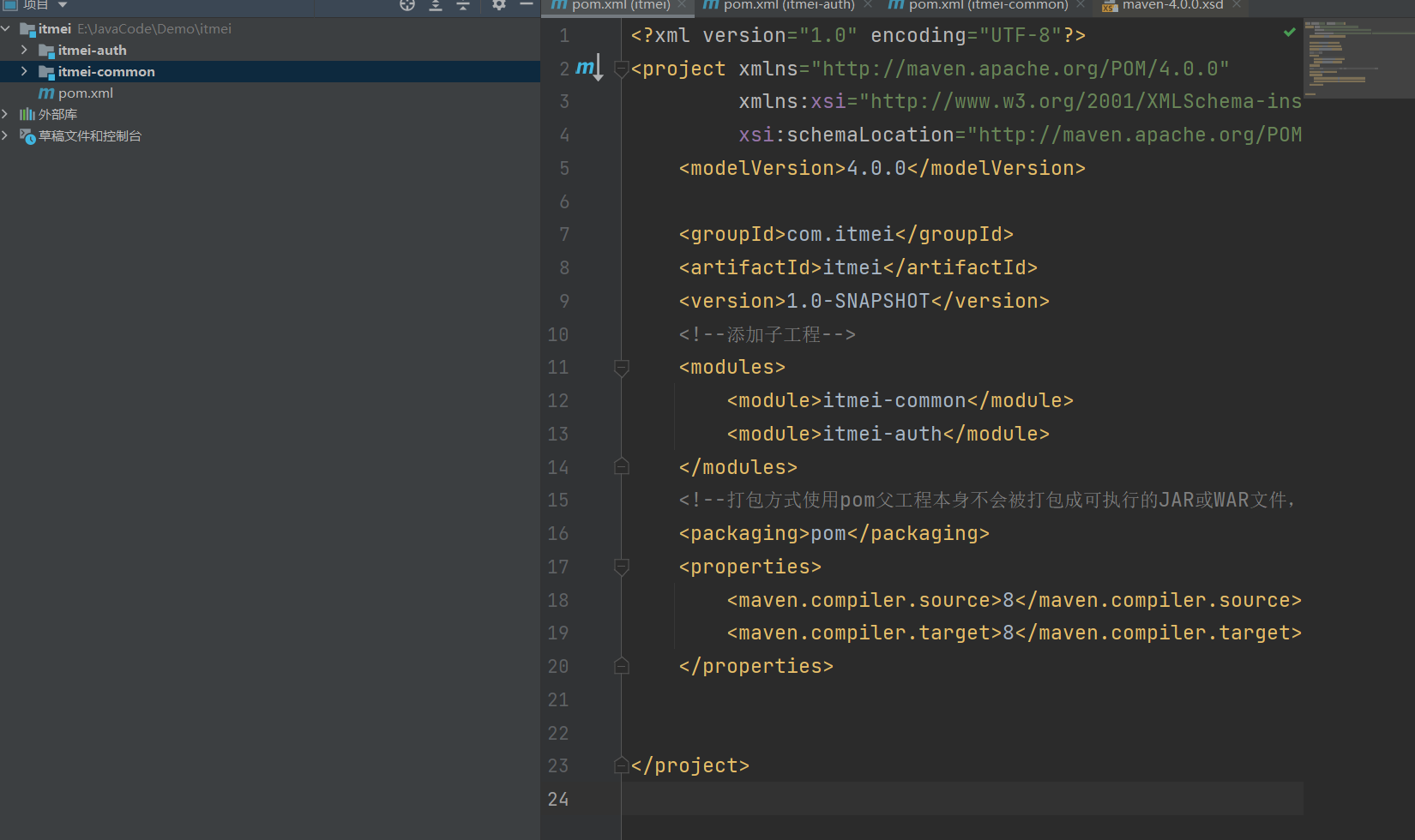
使用Maven创建父子工程
📚目录 创建父工程创建子模块创建子模块示例创建认证模块(auth) 结束 创建父工程 选择空项目: 设置:项目名称,组件名称,版本号等 创建完成后的工程 因为我们需要设置这个工程为父工程所以不需要src下的所有文件 在pom…...
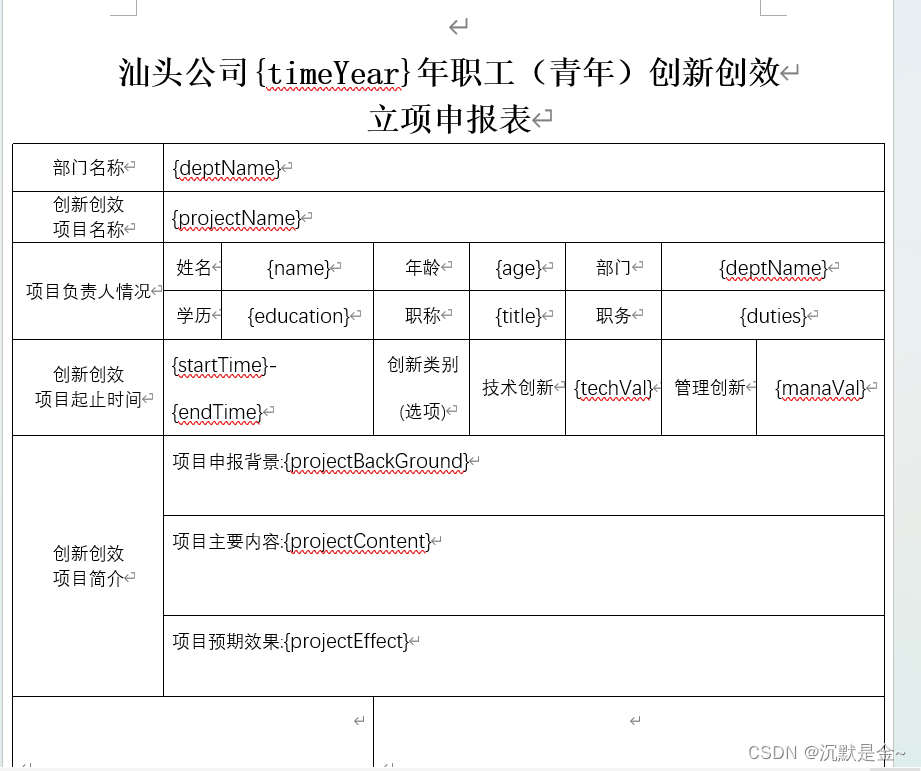
Vue+elementUI 导出word打印
import JSZipUtils from "jszip-utils"; import JSZip from "pizzip"; import Docxtemplater from "docxtemplater"; npm安装以上依赖 首先维护个word模板 导出方法 //导出wordskipOutWord(row) {var printData rowconst data JSON.parse(JS…...

数学建模-点评笔记 9月3日
1.摘要:关键方法和结论(精炼的语言)要说明,方法的合理性和意义也可以说明。 评委先通过摘要筛选(第一轮) 2.时间序列找异常值除了3西格玛还有针对时间序列更合适寻找的方法 3.模型的优缺点要写的详细一点…...
)
使用Spring来管理对象关系映射(ORM)
简介 对象关系映射(Object-Relational Mapping,简称ORM)是一种技术,用于在面向对象程序和关系型数据库之间进行数据的映射。Spring框架提供了强大的支持来简化和优化ORM开发过程。本文将介绍如何使用Spring来管理对象关系映射。 …...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...
