秒懂算法 | 子集树模型——0-1背包问题的回溯算法及动态规划改进

给定n种物品和一背包。物品i的重量是wi,其价值为vi,背包的容量为W。一种物品要么全部装入背包,要么全部不装入背包,不允许部分装入。装入背包的物品的总重量不超过背包的容量。问应如何选择装入背包的物品,使得装入背包中的物品总价值最大?
01、问题分析——解空间及搜索条件
根据问题描述可知,0-1背包问题要求找出n种物品集合{1,2,…,n}中的一部分物品,将这部分物品装入背包。装进去的物品总重量不超过背包的容量且价值之和最大,即找到n种物品集合{1,2,…,n}的一个子集,这个子集中的物品总重量不超过背包的容量,且总价值是集合{1,2,…,n}的所有不超过背包容量的子集中物品总价值最大的。
按照回溯法的算法框架,首先需要定义问题的解空间,然后确定解空间的组织结构,最后进行搜索。搜索前要解决两个关键问题,一是确定问题是否需要约束条件(用于判断是否有可能产生可行解),如果需要,那么应如何设置?二是确定问题是否需要限界条件(用于判断是否有可能产生最优解),如果需要,那么应如何设置?
1●定义问题的解空间
0-1背包问题是要将物品装入背包,并且物品有且只有两种状态。第i(i=1,2,…,n)种物品是装入背包能够达到目标要求,还是不装入背包能够达到目标要求呢?很显然,目前还不确定。因此,可以用变量xi表示第i种物品是否被装入背包的行为,如果用“0”表示不被
相关文章:

秒懂算法 | 子集树模型——0-1背包问题的回溯算法及动态规划改进
给定n种物品和一背包。物品i的重量是wi,其价值为vi,背包的容量为W。一种物品要么全部装入背包,要么全部不装入背包,不允许部分装入。装入背包的物品的总重量不超过背包的容量。问应如何选择装入背包的物品,使得装入背包中的物品总价值最大? 01、问题分析——解空间及搜索…...

koc转化效果评估模型是什么?如何根据模型来进行投放
目前小红书有超2亿月活用户,共有4300万的分享,当之无愧的成为众多年轻用户心中的“消费决策”平台。那怎么将如此巨大的流量切实的转化为效果是一个挑战。今天就来简单分享一下这个挑战的答案。其实可以借助模型来帮助,这就是koc转化效果评估…...

vuejs-datepicker|简单易用的Vue.js日期选择组件
vuejs-datepicker是一个简单易用的Vue.js日期选择组件。它使用了Bootstrap 4的样式,支持多种语言,具有直观的界面,易于配置和扩展。👉 效果演示 👉如果您想使用vuejs-datepicker,首先您需要安装它ÿ…...

【c++】类和对象3—初始化列表、类对象作为类成员、静态成员
文章目录初始化列表类对象作为类成员静态成员初始化列表 作用:c提供了初始化 语法:构造函数():属性1(值1),属性2(值2),…{} #include<iostream> using namespace std;class Person { public://1、传统初始化操作/*Person(int a, int b, int c) …...

【基础算法】数的范围
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...

FreeRTOS入门(01):基础说明与使用演示
文章目录目的基础说明系统移植基础使用演示数据类型和命名风格总结碎碎念目的 FreeRTOS是一个现在非常流行的实时操作系统(Real Time Operating System)。本文将介绍FreeRTOS入门使用相关内容,这篇是第一篇,主要介绍基础背景方面…...
)
华为OD机试真题Python实现【交换字符】真题+解题思路+代码(20222023)
交换字符 题目 给定一个字符串S 变化规则: 交换字符串中任意两个不同位置的字符M S都是小写字符组成 1 <= S.length <= 1000 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Python)真题目录汇总 输入 一串小写字母组成的字符串 输出 按照要求变换得到…...
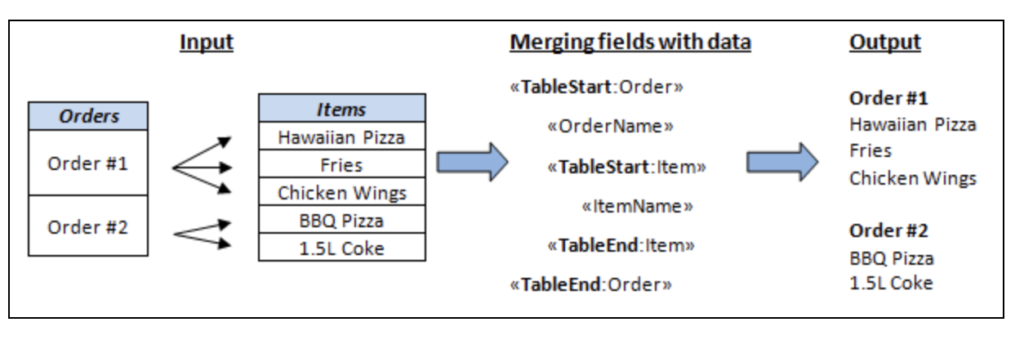
Word处理控件Aspose.Words功能演示:使用 Java 在 MS Word 文档中进行邮件合并
Aspose.Words 是一种高级Word文档处理API,用于执行各种文档管理和操作任务。API支持生成,修改,转换,呈现和打印文档,而无需在跨平台应用程序中直接使用Microsoft Word。此外,Aspose API支持流行文件格式处理…...

产品未出 百度朋友圈“开演”
ChatGPT这股AI龙卷风刮到国内时,人们齐刷刷望向百度,这家在国内对AI投入最高的公司最终出手了,大模型新项目文心一言(ERNIE Bot)将在3月正式亮相,对标微软投资的ChatGPT。 文心一言产品未出,百…...

emacs 中的键盘宏
emacs 中的键盘宏 宏定义是emacs比较强大的功能,自定义宏然后绑定快捷键之后就更加爽了。 vim 当然也有宏功能,而且用法简单,例如录制宏到a寄存器:qa...q, 执行宏a: a 世界就是由循环和递归构成的. 宏定义就是一个执行体,为了以后的循环做准备的 开启宏记录 C-x ( 或…...

TCP/IP网络编程——关于 I/O 流分离的其他内容
完整版文章请参考: TCP/IP网络编程完整版文章 文章目录第 16 章 关于 I/O 流分离的其他内容16.1 分离 I/O 流16.1.1 2次 I/O 流分离16.1.2 分离「流」的好处16.1.3 「流」分离带来的 EOF 问题16.2 文件描述符的的复制和半关闭16.2.1 终止「流」时无法半关闭原因16.2…...

【BCT认证_组播DNS】 DNS SRV RR
每天遇见几个罕为人知的Bug,醉了 定义 关键字“必须”、“不能”、“应该”、“不应该”和“可以”本文档中使用的术语应按照 [BCP 14] 中的规定进行解释。本文档中使用的其他术语在 DNS 中定义规范,RFC 1034。 适用性声明 一般情况下,预计…...
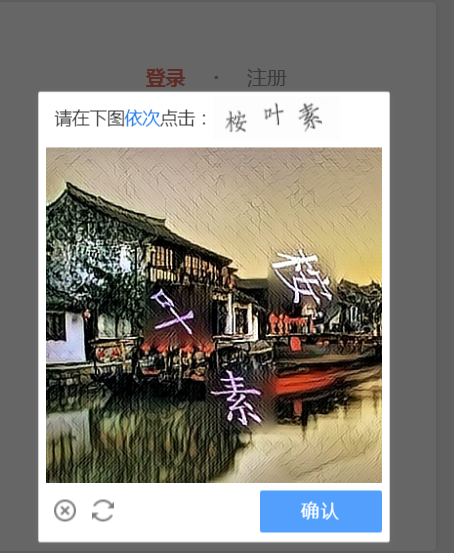
【验证码的识别】—— 点触式验证码的识别
一、前言 大家好,不知不觉的我来csdn已经又一周年了,在这一年里,我收获了很多东西,我是2022年2月22日入驻CSDN的,一开始只是为了方便浏览文章的,后来,我也有事没事发发文章,创作了1…...

深入浅出C++ ——priority_queue类深度剖析
文章目录一、priority_queue类简介二、priority_queue类常用接口三、priority_queue类的使用四、STL中priority_queue类的模拟实现一、priority_queue类简介 优先队列是一种容器适配器,根据严格的弱排序标准,它的第一个元素总是它所包含的元素中最大的。…...
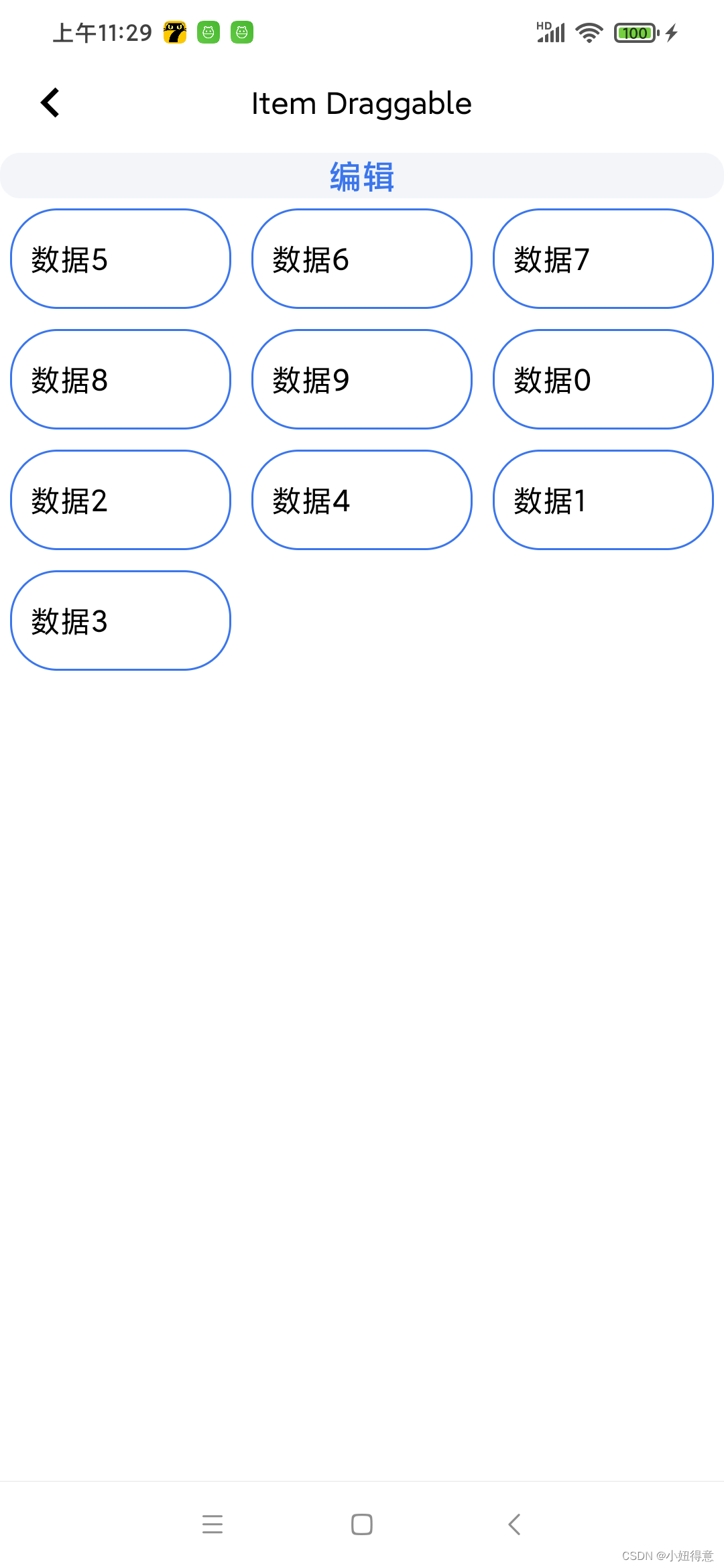
117.Android 简单的拖拽列表+防止越界拖动(BaseRecyclerViewAdapterHelper)
//1.第一步 导入依赖库和权限: //依赖库: //RecyclerView implementation com.android.support:recyclerview-v7:28.0.0//RecyclerAdapter implementation com.github.CymChad:BaseRecyclerViewAdapterHelper:2.9.28 //用到的权限: <!…...
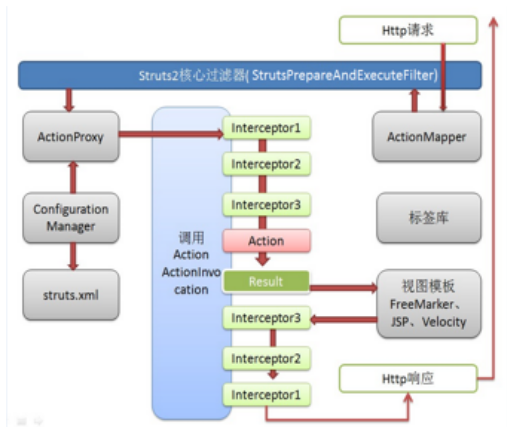
什么是Struts2?有哪些优势
Java中Strutsl是最早的基于MVC模式的轻量级Web框架,它能够合理地划分代码结构,并包含验证框架、国际化框架等多种实用工具框架。但是随着技术的进步,Struts1的局限性也越来越多地暴露出来。为了符合更加灵活、高效的开发需求,Stru…...
Ubuntu22.04 安装Mongodb6.X
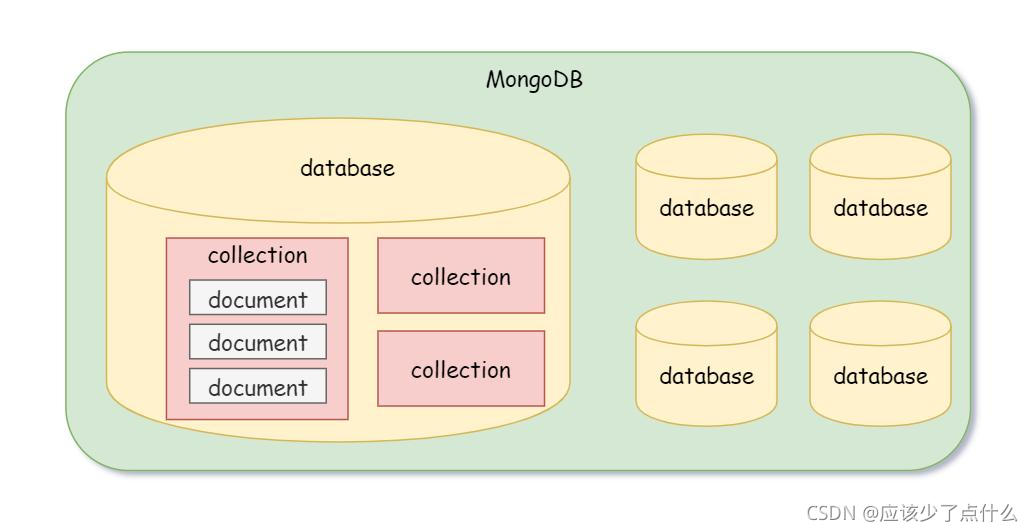
Ubuntu22.04 安装Mongodb6.X 1、Mongodb简介 1.1 什么是MongoDB? Mongodb是一个跨平台的面向文档的NoSQL数据库。它使用带有可选模式的类似JSON的BSON来存储数据。应用程序可以以JSON格式检索信息。 1.2 MongoDB的优点 可以快速开发web型应用,因为灵活,…...
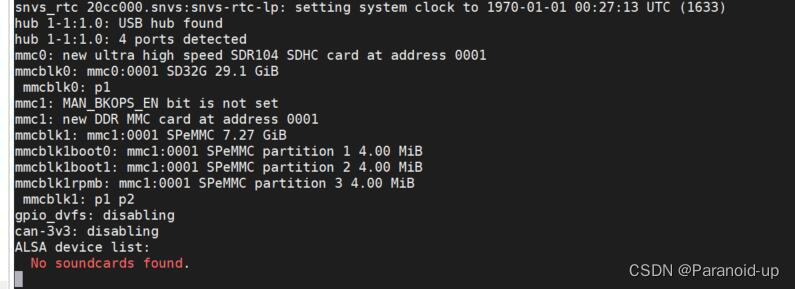
启动内核,能启动内核但是无法进入内核,始终卡在某一地方,比如 No soundcards found.
项目场景: 配置好uboot后,启动内核,能启动内核但是无法进入内核,始终卡在某一地方,比如下图 ALSA device list:No soundcards found.问题描述 原因分析: 这是无法进入根文件系统而出现的错误,…...
SQL零基础入门学习(六)
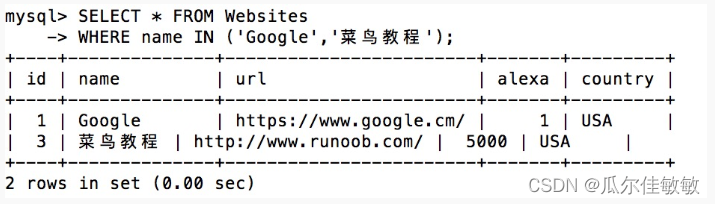
SQL零基础入门学习(六) SQL零基础入门学习(五) SQL 通配符 通配符可用于替代字符串中的任何其他字符。 SQL 通配符用于搜索表中的数据。 在 SQL 中,可使用以下通配符: 演示数据库 在本教程中ÿ…...
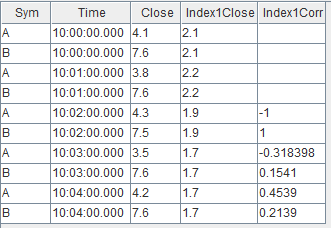
股票、指数、快照、逐笔... 不同行情数据源的实时关联分析应用
在进行数据分析时经常需要对多个不同的数据源进行关联操作,因此在各类数据库的 SQL 语言中均包含了丰富的 join 语句,以支持批计算中的多种关联操作。 DolphinDB 不仅通过 join 语法支持了对于全量历史数据的关联处理,而且在要求低延时的实时…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...

JavaScript 标签加载
目录 JavaScript 标签加载script 标签的 async 和 defer 属性,分别代表什么,有什么区别1. 普通 script 标签2. async 属性3. defer 属性4. type"module"5. 各种加载方式的对比6. 使用建议 JavaScript 标签加载 script 标签的 async 和 defer …...
