洛谷 Array 数论
题目:
对于长度为n的数组A,A中只包含从1到n的整数(可重复)。如果A单调不上升或单调不下降,A就可称为美丽的。 找出在长度为n时,有几个美丽的A。
思路:
这是一道数论题。
我们先找找“单调不递减的A”。
1.构造模型:设一个长度为(2*n-1)的序列,用1填满n个空,剩余(n-1)个空;
2.一一对应:找到每一个“1”,用其前方总共的“空格数”构成新序列。如下图所示。
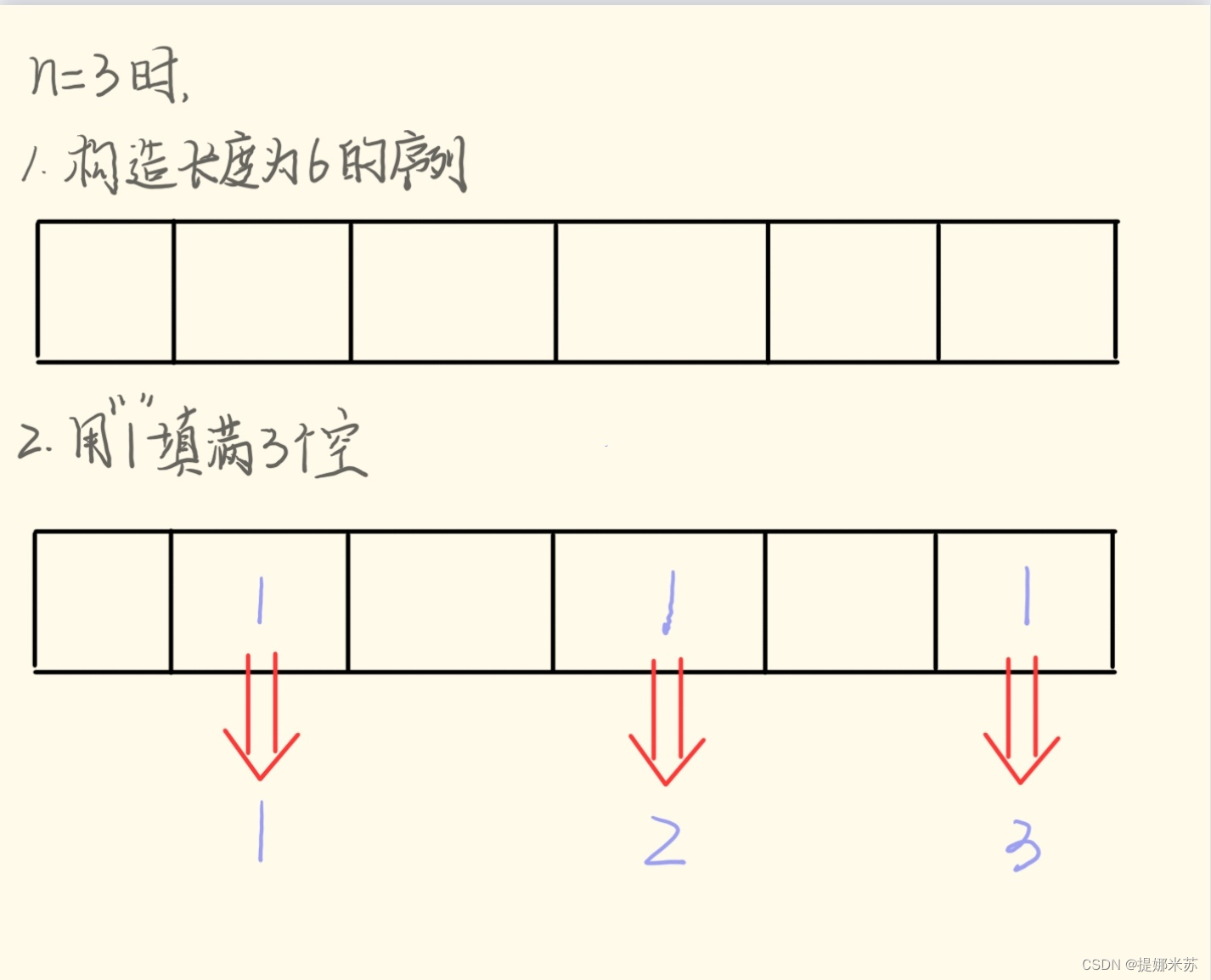
3.合理性:构成的序列满足两个条件。
- (1)不递减:因为空格的数目只会累加。(如果两个“1”相邻的话会出现新序列中有相同数字的情况)
- (2)新序列中每个数字都是0到n-1的整数(可重复)对应题干中“从1到n的整数”:因为空格的数目最多只有n-1。
可见,单调不递减的A的数目=。
易得,单调不递增的A的数目=单调不递减的A的数目=。
所以,由容斥定理得,答案=不递增+不递减-既不递增.也不递减(常数序列) .
代码展示:
#include<stdio.h>
#include<stdlib.h>
const int mod=1000000007;
long long ny(long long x)//逆元 取模
{int cf=mod-2;long long base=x,ans=1;while(cf){if(cf%2==1) ans*=base;ans%=mod;base=base*base;base%=mod;cf>>=1;}return ans;
}
long long c(int x,int y)//计算组合数
{long long fz=1,fm=1,ans;int i;for(i=x;i>=x-y+1;i--) {fz*=i;fz%=mod;}for(i=1;i<=y;i++){fm*=i;fm%=mod;}fm=ny(fm);ans=fz*fm;ans%=mod;return ans;
}
long long zj;
int main()
{//答案是c(2n,n)-n int n,i;scanf("%d",&n);zj=c(2*n,n);zj-=n;if(zj<0) zj+=mod;printf("%lld",zj);return 0;
}
相关文章:
洛谷 Array 数论
题目: 对于长度为n的数组A,A中只包含从1到n的整数(可重复)。如果A单调不上升或单调不下降,A就可称为美丽的。 找出在长度为n时,有几个美丽的A。 思路: 这是一道数论题。 我们先找找“单调不递…...
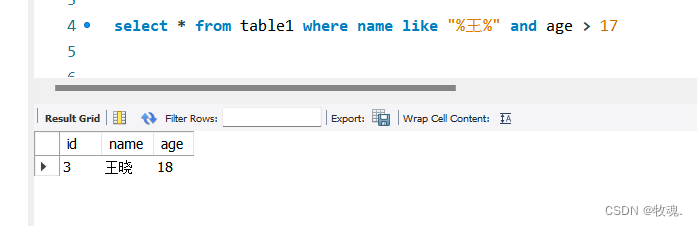
简明SQL条件查询指南:掌握WHERE实现数据筛选
条件查询是用于从数据库中根据特定条件筛选数据行的一种方式,它避免了检索整个表中的数据。通常,使用 WHERE 子句来定义过滤条件,只有符合这些条件的数据行才会被返回。 SQL中的运算符有:、!、<、> 等,用于进行…...

通过HbaseClient来写Phoenix表实现
由于数据存储在Hbase上,并且上层使用了Phoenix来读写数据。并且由于数据的列字段不固定,并且可能由于Hbase表列和Phoenix的表列字段不一致,使用Phoenix写入的数据会导致写出报错的问题出现。所以这里直接使用HbaseClient写入到Hbase表中&…...

uniapp qiun charts H5使用echarts的eopts配置不生效
原因是:使用web的要设置 echartsH5 :echartsH5"true" <template><view class"charts-box"><view class"chart-title"> 趋势</view><qiun-data-chartstype"column":eopts"eopts":cha…...

嵌入式Linux驱动开发(LCD屏幕专题)(三)
1. 硬件相关的操作 LCD驱动程序的核心就是: 分配fb_info设置fb_info注册fb_info硬件相关的设置 硬件相关的设置又可以分为3部分: 引脚设置时钟设置LCD控制器设置 2. 在设备树里指定LCD参数 framebuffer-mylcd {compatible "100ask,lcd_drv&qu…...

MySQL视图用户管理
文章目录 视图视图的规则用户用户信息创建用户删除用户修改密码 用户权限给用户授权回收权限 视图 视图是一个虚拟表,其内容由查询定义。同真实的表一样,视图包含一系列带有名称的列和行数据。视图的数据变化会影响到基表,基表的数据变化也会…...
我发现了一个很好看的字体,霞鹜文楷!如何换windows和typora字体?
1、字体 官方地址如下,下载也很简单。 https://github.com/lxgw/LxgwWenKai 有1W多的stars。 方式: 直接打包下载。下载不来,可以联系我。 然后ttf的文件,全部安装就行了。 reg save "HKCU\Control Panel" .\res…...

微软8月系统更新引发问题:虚拟内存分页文件出现错误
微软的八月系统更新引发了一系列问题,其中包括“UNSUPPORTED_PROCESSOR”蓝屏错误和文件管理器故障。尽管微软已经修复了前者,但据国外科技媒体Windows Latest报道,仍有用户反馈在非微星设备上出现“fault in nonpaged area”蓝屏错误。 如果…...
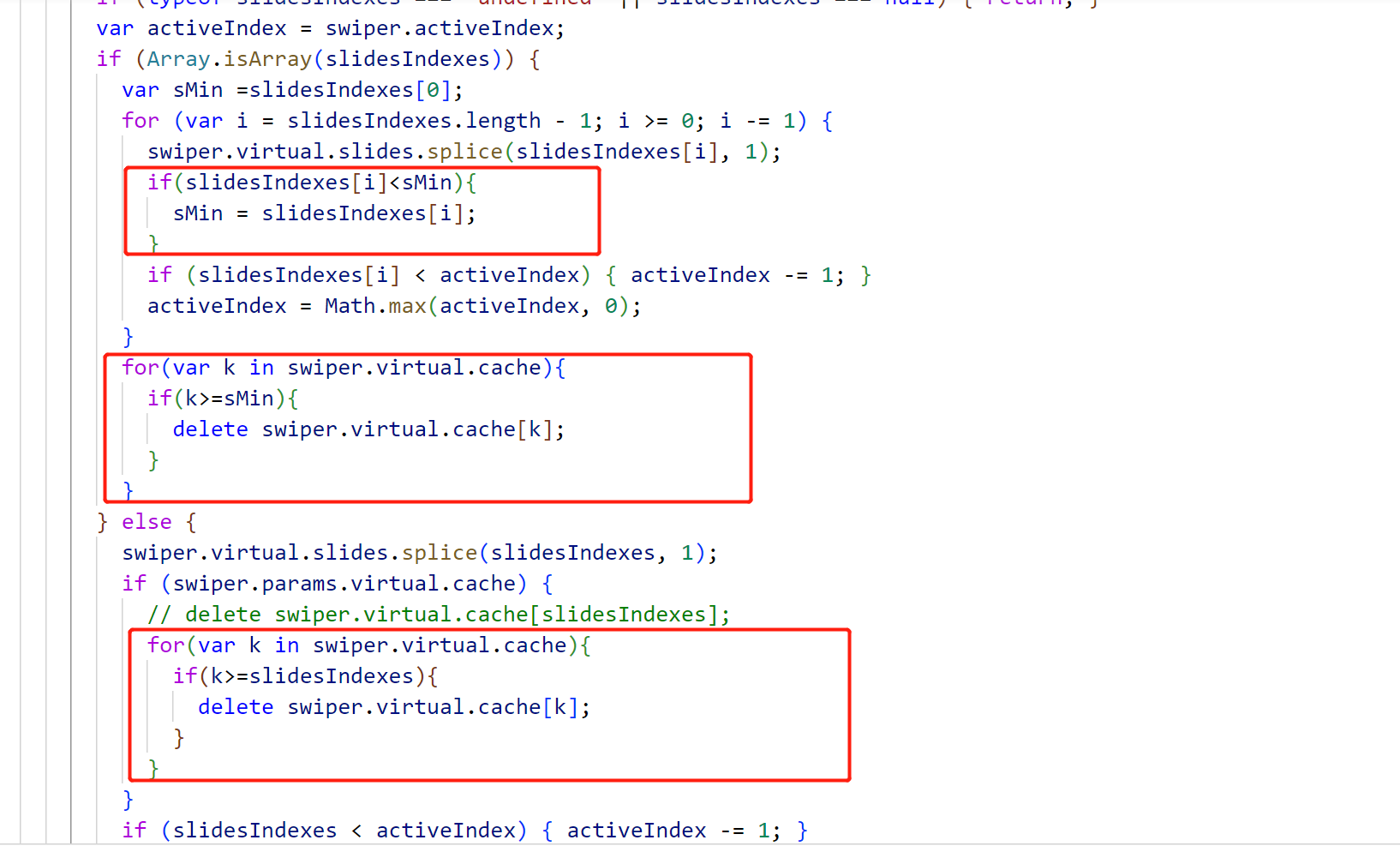
swiper删除虚拟slide问题
在存在缓存的情况下,删除较前的slide,会出现当前slide与后一个slide重复出现的情况 假设当前存在5个slide,且这5个slide已缓存,则删除slide2后,仍为5个slide,且slide2的内容变为slide3的内容,此…...

FPGA实战小项目2
基于FPGA的贪吃蛇游戏 基于FPGA的贪吃蛇游戏 基于fpga的数字密码锁ego1 基于fpga的数字密码锁ego1 基于fpga的数字时钟 basys3 基于fpga的数字时钟 basys3...

一些关于完整小程序项目的优秀开源
转载自: 35个项目,开源,开源! (qq.com) 那几本霸占我休息时间的PDF! (qq.com) 13个超强的 SpringBoot 实战项目 (还不赶紧收藏起来) (qq.com) 用SpringBoot开发一个人脸识别系统!…...

Windows模拟器推荐
物是人非事事休,欲语泪先流 Windows模拟器推荐 如果你需要在 Windows 操作系统之外运行 Windows 应用程序或测试不同版本的 Windows,有几个 Windows 模拟器和虚拟机软件可供选择。以下是一些常用的 Windows 模拟器和虚拟机软件: VirtualBox&…...

搭建RabbitMQ消息服务,整合SpringBoot实现收发消息
作者主页:Designer 小郑 作者简介:3年JAVA全栈开发经验,专注JAVA技术、系统定制、远程指导,致力于企业数字化转型,CSDN博客专家,蓝桥云课认证讲师。 目录 一、前言1.1 什么是消息队列1.2 RabbitMQ 是什么1.…...
Web framework-Gin(二)
目录 一、Gin 1、Ajax 2、文件上传 2.1、form表单中文件上传(单个文件) 2.2、form表单中文件上传(多个文件) 2.3、ajax上传单个文件 2.4、ajax上传多个文件 3、模板语法 4、数据绑定 5、路由组 6、中间件 一、Gin 1、Ajax AJAX 即“Asynchronous Javascript And XM…...
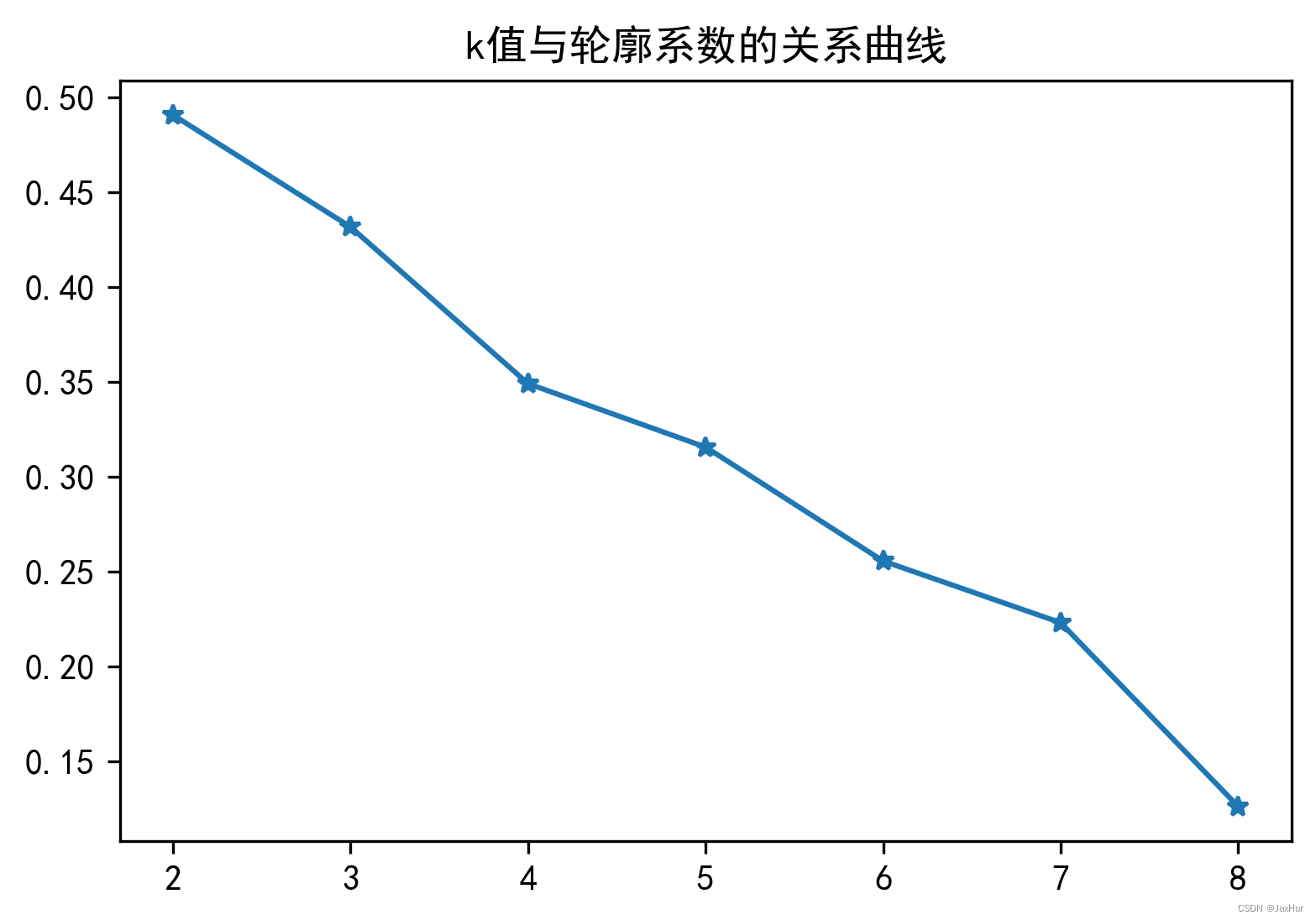
【聚类】K-Means聚类
cluster:簇 原理: 这边暂时没有时间具体介绍kmeans聚类的原理。简单来说,就是首先初始化k个簇心;然后计算所有点到簇心的欧式距离,对一个点来说,距离最短就属于那个簇;然后更新不同簇的簇心&a…...
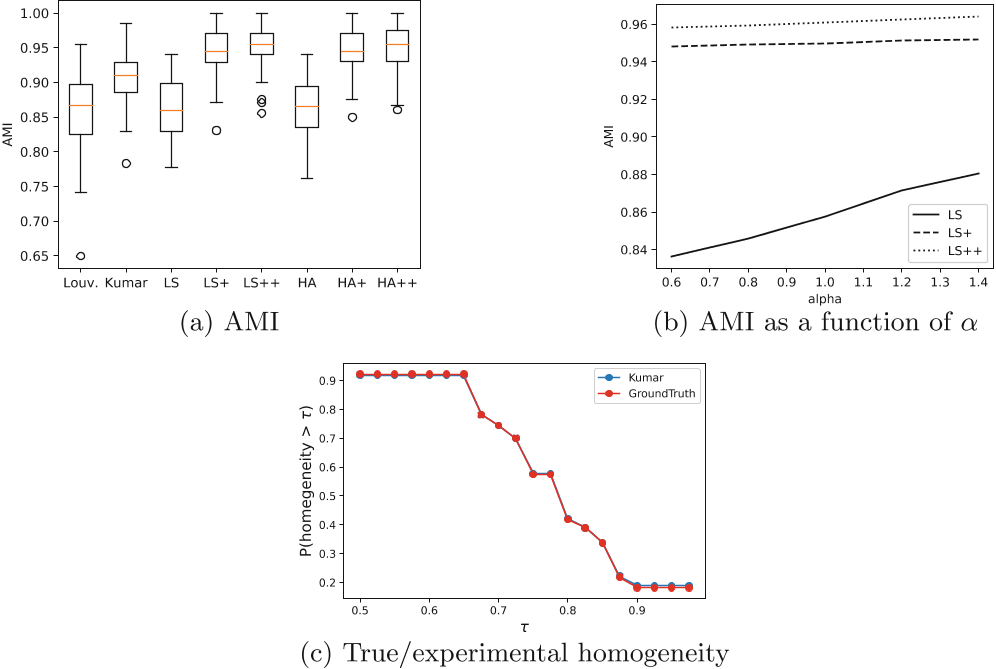
超图聚类论文阅读2:Last-step算法
超图聚类论文阅读2:Last-step算法 《使用超图模块化的社区检测算法》 《Community Detection Algorithm Using Hypergraph Modularity》 COMPLEX NETWORKS 2021, SCI 3区 具体实现源码见HyperNetX库 工作:提出了一种用于超图的社区检测算法。该算法的主要…...

React 防抖与节流用法
在React中,防抖和节流是优化性能和提升用户体验的常用技术。下面是它们的用法: 防抖(Debounce):防抖是指在某个事件触发后,等待一段时间后执行回调函数。如果在等待时间内再次触发该事件,将重新…...

发布 VectorTraits v1.0,它是 C# 下增强SIMD向量运算的类库
发布 VectorTraits v1.0, 它是C#下增强SIMD向量运算的类库 VectorTraits: SIMD Vector type traits methods (SIMD向量类型的特征方法). NuGet: https://www.nuget.org/packages/VectorTraits/1.0.0 源代码: https://github.com/zyl910/VectorTraits 用途 总所周知&#x…...

HCIA自学笔记01-冲突域
共享式网络(用同一根同轴电缆通信)中可能会出现信号冲突现象。 如图是一个10BASE5以太网,每个主机都是用同一根同轴电缆来与其它主机进行通信,因此,这里的同轴电缆又被称为共享介质,相应的网络被称为共享介…...

3D封装技术发展
长期以来,芯片制程微缩技术一直驱动着摩尔定律的延续。从1987年的1um制程到2015年的14nm制程,芯片制程迭代速度一直遵循摩尔定律的规律,即芯片上可以容纳的晶体管数目在大约每经过18个月到24个月便会增加一倍。但2015年以后,芯片制…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

CTF show 数学不及格
拿到题目先查一下壳,看一下信息 发现是一个ELF文件,64位的 用IDA Pro 64 打开这个文件 然后点击F5进行伪代码转换 可以看到有五个if判断,第一个argc ! 5这个判断并没有起太大作用,主要是下面四个if判断 根据题目…...
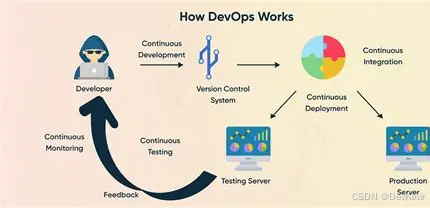
持续交付的进化:从DevOps到AI驱动的IT新动能
文章目录 一、持续交付的本质:从手动到自动的交付飞跃关键特性案例:电商平台的高效部署 二、持续交付的演进:从CI到AI驱动的未来发展历程 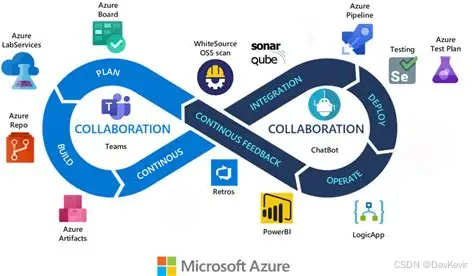中国…...
