当前位置： 首页 > news >正文

软考：中级软件设计师:程序语言基础：表达式，标准分类，法律法规，程序语言特点，函数传值传址

news 2026/2/10 19:07:01

软考：中级软件设计师:程序语言基础：表达式

提示：系列被面试官问的问题，我自己当时不会，所以下来自己复盘一下，认真学习和总结，以应对未来更多的可能性

关于互联网大厂的笔试面试，都是需要细心准备的
（1）自己的科研经历，科研内容，学习的相关领域知识，要熟悉熟透了
（2）自己的实习经历，做了什么内容，学习的领域知识，要熟悉熟透了
（3）除了科研，实习之外，平时自己关注的前沿知识，也不要落下，仔细了解，面试官很在乎你是否喜欢追进新科技，跟进创新概念和技术
（4）准备数据结构与算法，有笔试的大厂，第一关就是手撕代码做算法题
面试中，实际上，你准备数据结构与算法时以备不时之需，有足够的信心面对面试官可能问的算法题，很多情况下你的科研经历和实习经历足够跟面试官聊了，就不需要考你算法了。但很多大厂就会面试问你算法题，因此不论为了笔试面试，数据结构与算法必须熟悉熟透了
秋招提前批好多大厂不考笔试，直接面试，能否免笔试去面试，那就看你简历实力有多强了。
（5）考网警的大佬，务必把软考：中级软件设计师的内容学好学透，学广，学多

文章目录

  • 软考：中级软件设计师:程序语言基础：表达式
    • @[TOC](文章目录)
  • 软考：中级软件设计师:程序语言基础：表达式
  • 函数调用的传值与传址
  • 各种程序语言的特点
  • 法律法规
  • 标准分类
  • 总结

软考：中级软件设计师:程序语言基础：表达式

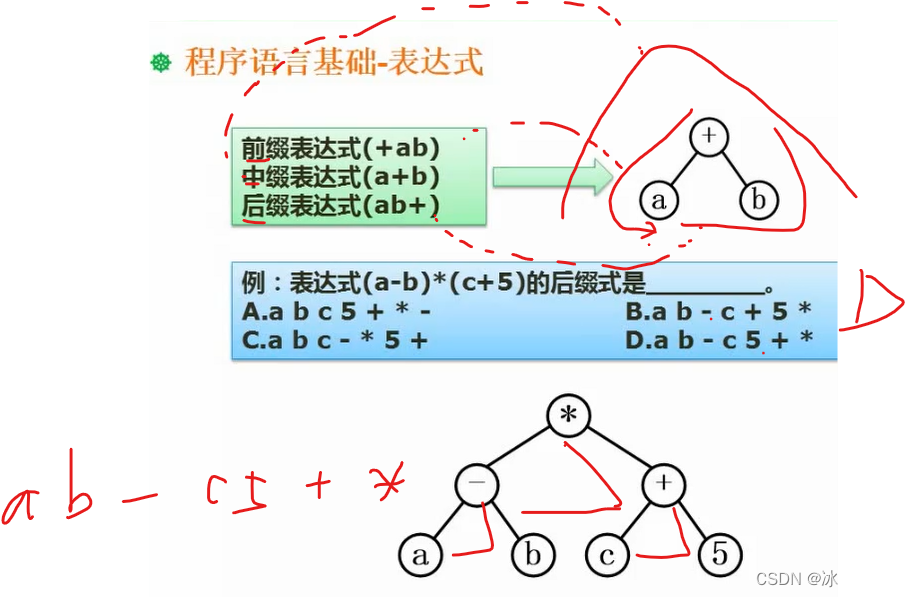
在这里插入图片描述
前缀，中缀，后缀
就是算法中前序，中序，后序

先构造树，再考虑二叉树的遍历
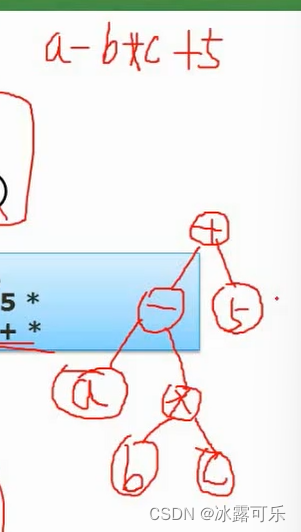
在这里插入图片描述
括号决定了先后顺序，但是不要构造到树中

函数调用的传值与传址

常考的考题

在这里插入图片描述
看形式参数试是啥？实际参数是啥？
一个是象征代表
一个是实际代表
在这里插入图片描述

传值：直接把实际代表值，给形式代表表，即实参传给形参
形参内部变化，跟实参无关哦
是真的赋值

传址：传递地址*p

把实参的地址传递个形参，那形参被操作了，自然就是代表操作地址中的实际变量
所以函数形改变，必定改变实参

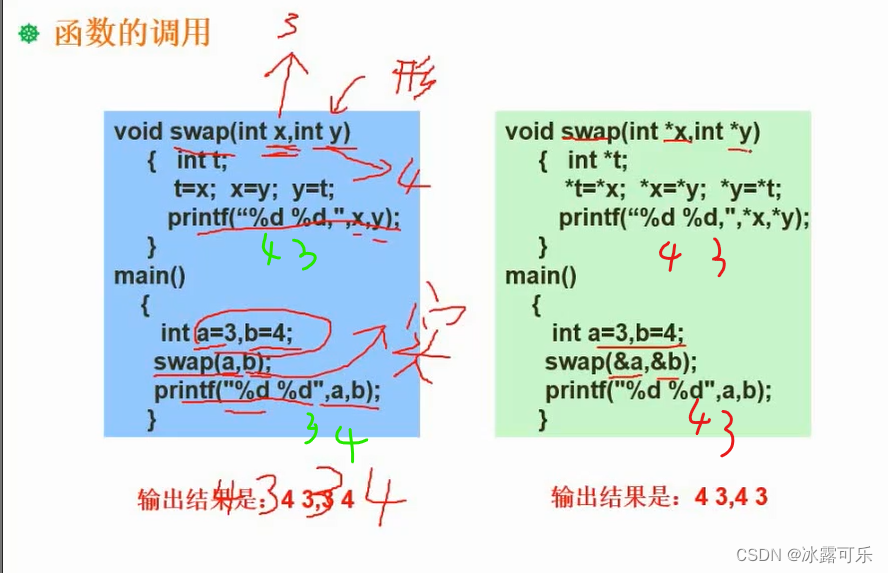
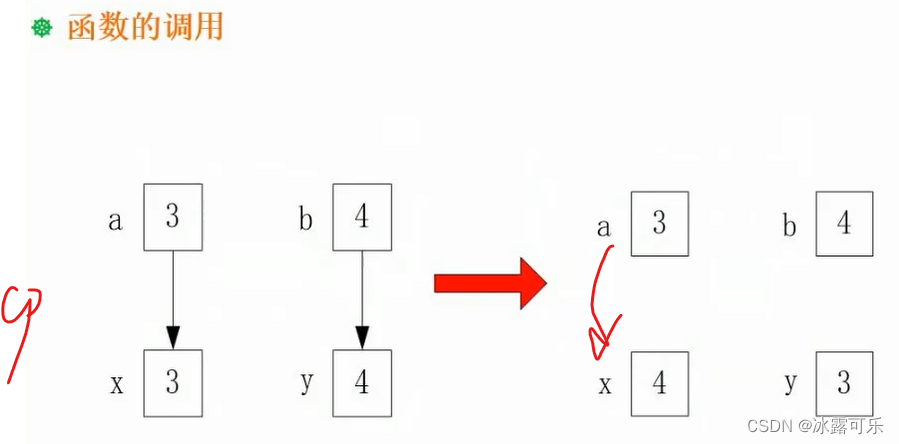
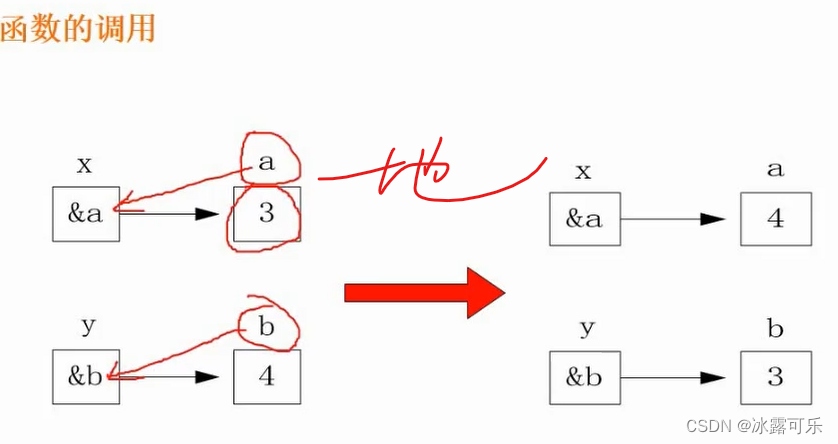
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
easy

各种程序语言的特点

在这里插入图片描述
python大数据，AI

法律法规

考2–3分
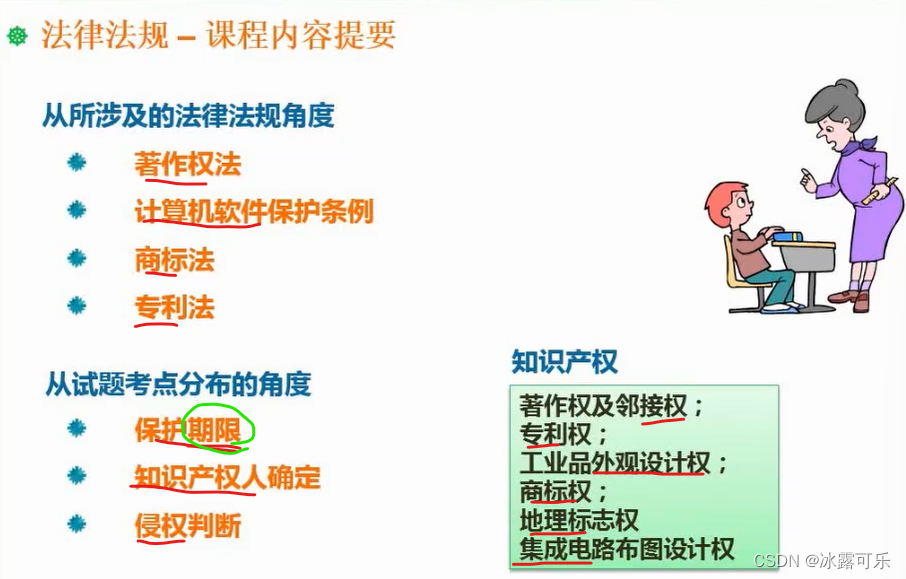
在这里插入图片描述
在这里插入图片描述

标准分类

代号是什么类型的标准

在这里插入图片描述

总结

提示：重要经验：

1）
2）
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。

相关文章：

软考：中级软件设计师:程序语言基础：表达式，标准分类，法律法规，程序语言特点，函数传值传址

软考：中级软件设计师:程序语言基础：表达式 提示：系列被面试官问的问题，我自己当时不会，所以下来自己复盘一下，认真学习和总结，以应对未来更多的可能性 关于互联网大厂的笔试面试，都…...

编程日记 2023/9/8 20:02:49

Java“牵手”1688商品详情数据，1688商品详情API接口，1688API接口申请指南

1688平台商品详情接口是开放平台提供的一种API接口，通过调用API接口，开发者可以获取1688商品的标题、价格、库存、月销量、总销量、库存、详情描述、图片等详细信息 。 获取商品详情接口API是一种用于获取电商平台上商品详情数据的接口，通过…...

编程日记 2023/9/8 20:01:48

stable diffusion实践操作-批次出图

系列文章目录 stable diffusion实践操作 文章目录 系列文章目录前言一、批次出图介绍1.1 webUI设置1.2 参数介绍 二、批次出图使用2.1 如何设置2.1 效果展示 总结 前言 本章主要介绍SD批次出图。 想要一次产生多张图片的时候使用。 一、批次出图介绍 1.1 webUI设置 1.2 参数…...

编程日记 2023/9/8 20:00:47

LeetCode热题100 【cpp】题解（一）哈希表和双指针

文章目录 1. 两数之和49. 字母异位词分组128. 最长连续序列283. 移动零11. 盛最多水的容器15. 三数之和42. 接雨水 题单链接： LeetCode 热题 100 1. 两数之和 leetcode题目链接 题解1：暴力枚举 时间复杂度： O ( n 2 ) O(n^2) O(n2) class …...

编程日记 2023/9/8 19:59:44

Python爬虫常见代理池实现和优化

在这篇文章中，我们将探讨Python爬虫中常见的代理池实现和优化方法。在爬取网站数据时，为防止被目标网站封禁IP，我们通常会使用代理IP进行访问。一个高效且稳定的代理池可以帮助我们轻松应对各种反爬策略。 　　首先，我们来了解一下…...

编程日记 2023/9/8 19:58:43

前端面试的话术集锦第 3 篇：进阶篇上

这是记录前端面试的话术集锦第三篇博文——进阶篇上，我会不断更新前端面试话术的博文。❗❗❗ 1 谈谈变量提升 当执⾏JS代码时，会⽣成执⾏环境，只要代码不是写在函数中的，就是在全局执⾏环境中，函数中的代码会产⽣函数执⾏环境，只此两种执⾏环境。 b() // call b conso…...

编程日记 2023/9/8 19:57:41

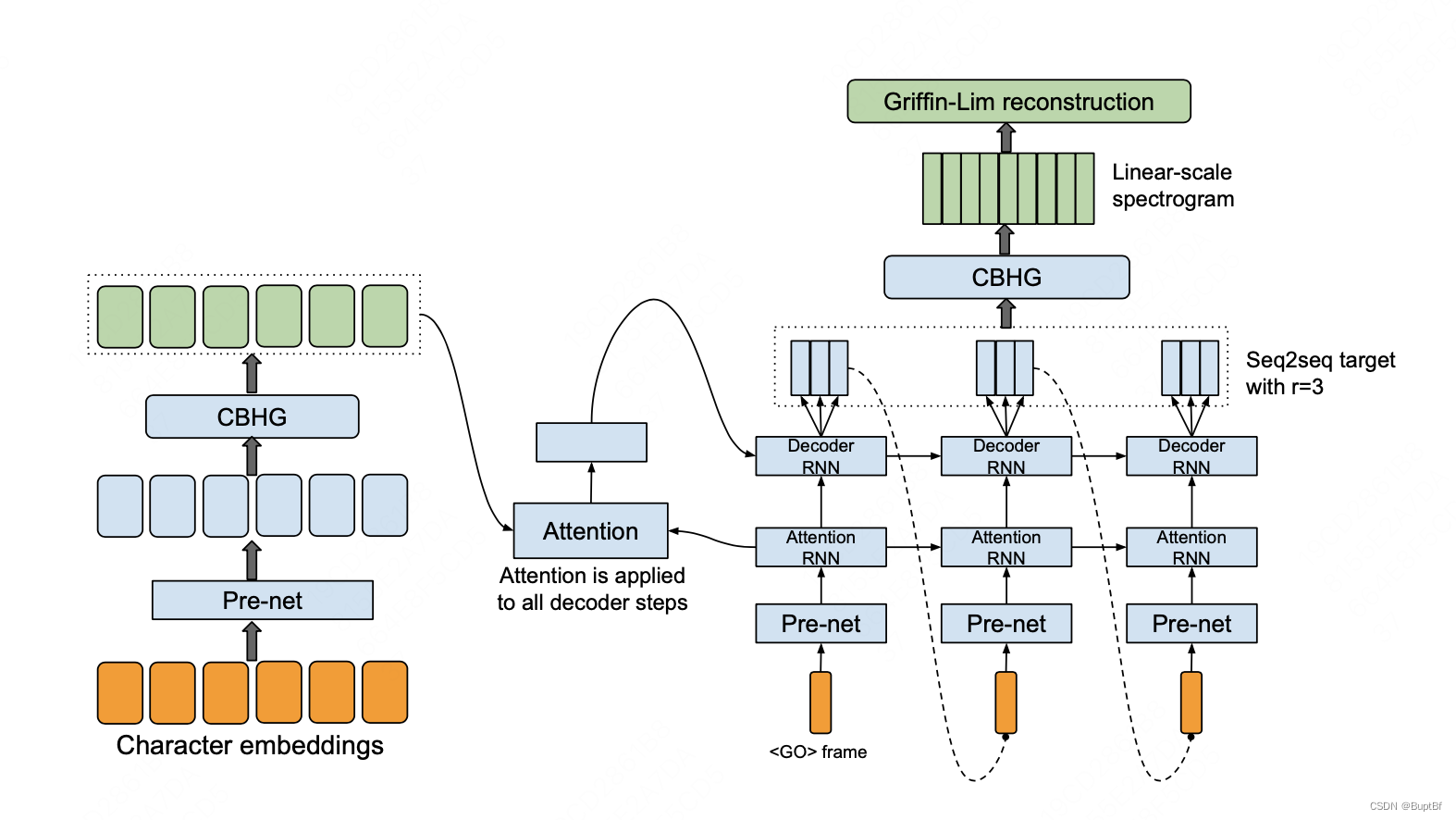
【文字到语音的论文总结】

1.文字到语音的整个过程 文字到语音的一般整体结构 主要是下面这个流程，每个网络可能会把其中两者或是三者融合在一起来； 长度不同的问题 生成的语音可能和文字的长度并不一样，因此需要解决这个问题 Tactron使用的是交叉注意力的方式解…...

编程日记 2023/9/8 19:56:40

E. Data Structures Fan(思维 + 异或前缀和)

Problem - E - Codeforces 给你一个整数数组 a1, a2,..., an，以及一个由 n 个字符组成的二进制字符串† s。 Augustin 是一个数据结构的爱好者。因此，他请你实现一个可以回答 q 个查询的数据结构。这里有两种类型的查询： Plain Text "1…...

编程日记 2023/9/8 19:55:39

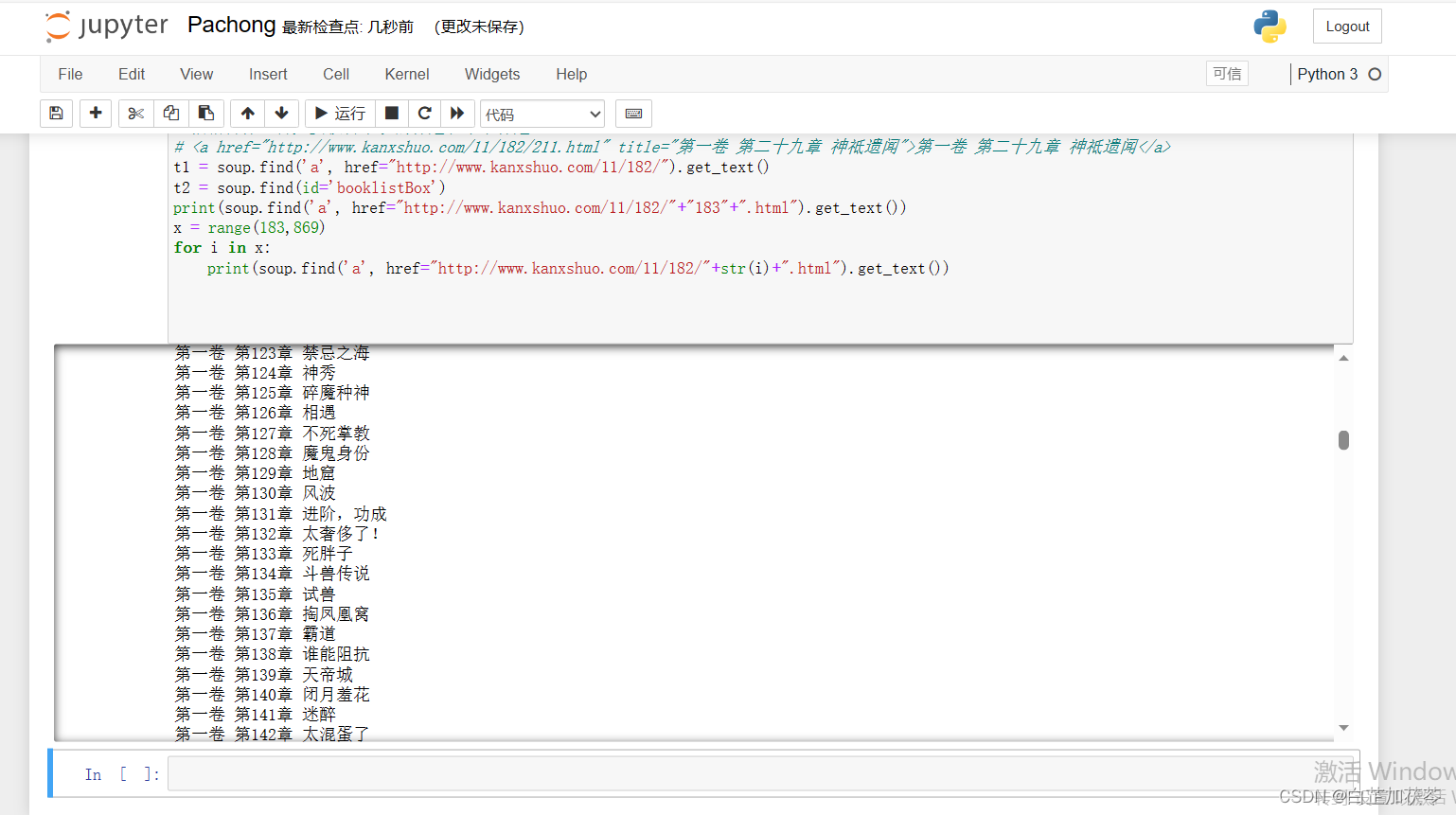
初学python爬虫学习笔记——爬取网页中小说标题

初学python爬虫学习笔记——爬取网页中小说标题 一、要爬取的网站小说如下图 二、打开网页的“检查”，查看html页面 发现每个标题是列表下的一个个超链接，从183.html到869.html 可以使用for循环依次得到： x range(183,600) for i in x:pr…...

编程日记 2023/9/8 19:54:37

The WebSocket session [x] has been closed and no method (apart from close())

在向客户端发送消息时，session关闭了。 不管是单客户端发送消息还是多客户端发送消息，在发送消息之前判断session 是否关闭 使用 isOpen() 方法...

编程日记 2023/9/8 19:53:36

前端实现展开收起的效果 (react)

需求背景：需要实现文本的展开收起效果，文本是一行一行的，数据格式是数组结构。 如图所示（图片已脱敏） 简单实现：使用一个变量控制展开收起效果。 展开收起逻辑部分（react） const […...

编程日记 2023/9/8 19:52:35

ABY2.0：更低的通信开销

参考文献： [ABY] Demmler D, Schneider T, Zohner M. ABY-A framework for efficient mixed-protocol secure two-party computation[C]//NDSS. 2015.[ABY3] Mohassel P, Rindal P. ABY3: A mixed protocol framework for machine learning[C]//Proceedings of the…...

编程日记 2023/9/8 19:51:33

vue项目预览图片

1.图片为本地上传的预览&#xff1a; <input type"file" ref"file"/> <img :src"imgUrl"/>let fr new FileReader()fr.readAsArrayBuffer(this.$refs.file.files[0])fr.addEventListener("loadend", (e) > {let buff…...

编程日记 2023/9/8 19:50:31

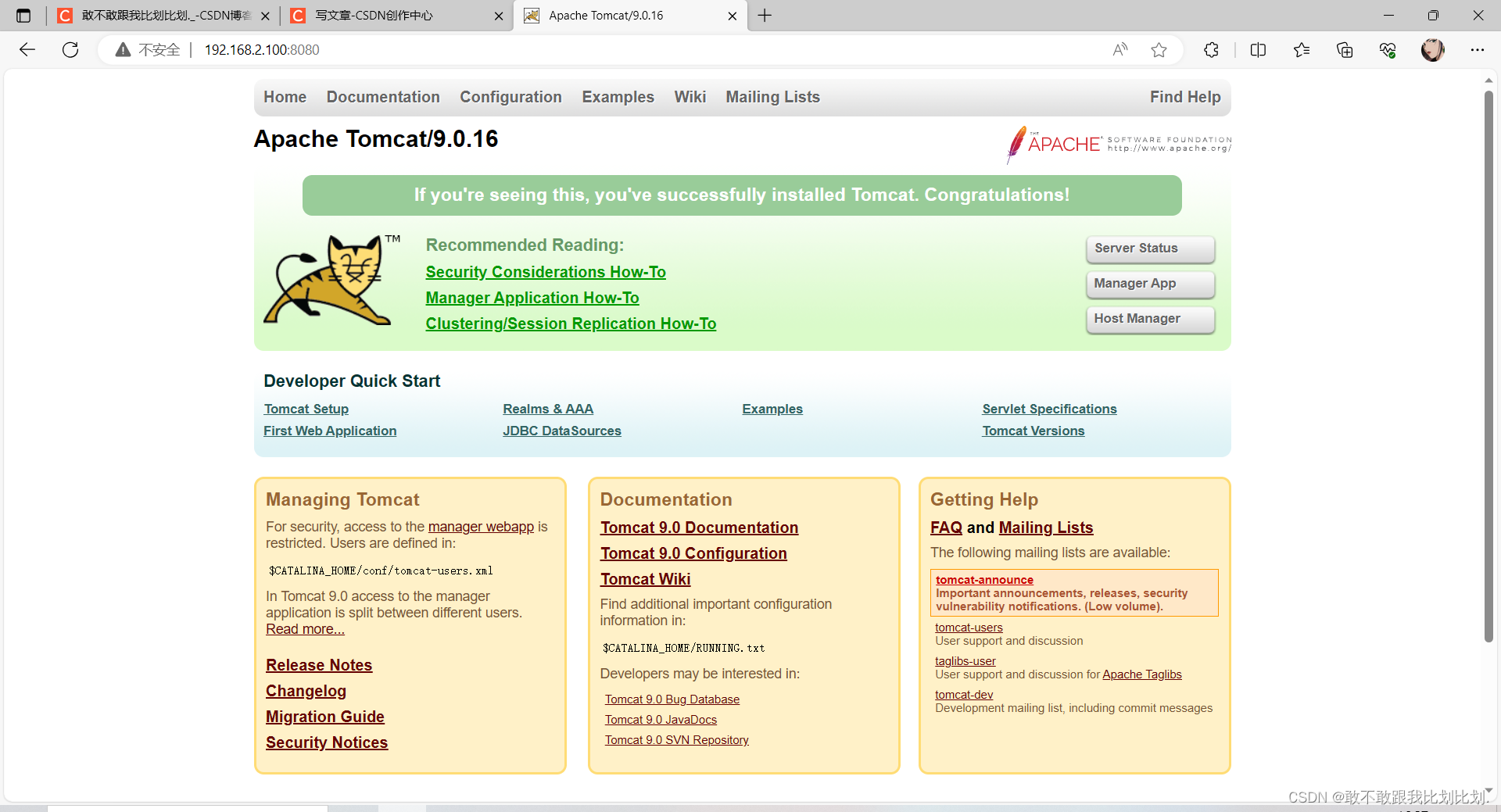
Tomcat 安装

1.关闭防火墙 2.安装JDK包 3. 4。添加环境变量 5.刷新配置文件 6.解压文件 7.启动tomcat 8. 9.编写tomcat.service文件 vim /etc/systemd/system/tomcat.service 10.刷新服务 11.打开浏览器访问&#xff1a;192.168.2.100:8080/&#xff0c;正常可以看到以下界面...

编程日记 2023/9/8 19:49:29

计算机网络的故事——HTTP报文内的HTTP信息

HTTP报文内的HTTP信息 文章目录 HTTP报文内的HTTP信息一、HTTP 报文二、请求报文及响应报文的结构三、编码提升传输速率 一、HTTP 报文 HTTP报文是由多行&#xff08;CRLF作换行符&#xff09;数据构成的字符串文本&#xff0c;HTTP报文可以分为报文首部和报文主体两部分&…...

编程日记 2023/9/8 19:48:28

CF1120 D. Power Tree 巧妙的图论转化

传送门 [前题提要]:无 题目描述: 就是给你一棵树,然后每个点有花费,然后你可以选一个点,付费后对这个点的子树的所有叶子结点增减任意权值. 考虑有一个人会给这棵树的所有叶子结点赋值(值我们不知道),输出最小的花费,使得无论它如何赋值,我们使用上述的花 费都能使所有的叶子…...

编程日记 2023/9/8 19:47:27

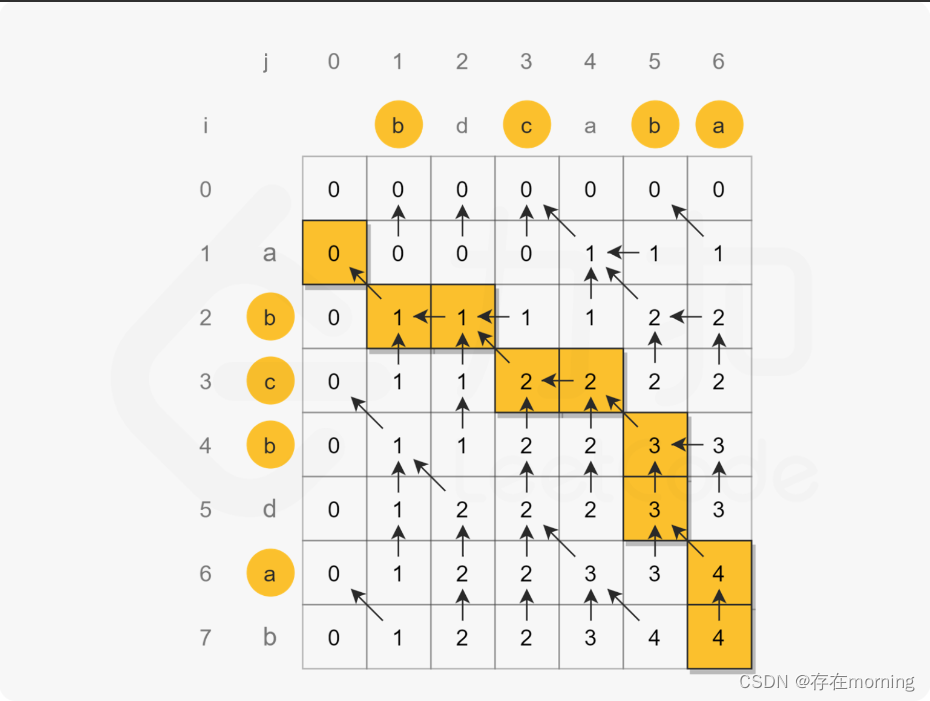
【算法训练-字符串 三】最长公共子串、最长公共子序列

废话不多说&#xff0c;喊一句号子鼓励自己&#xff1a;程序员永不失业&#xff0c;程序员走向架构&#xff01;本篇Blog的主题是【】&#xff0c;使用【】这个基本的数据结构来实现&#xff0c;这个高频题的站点是&#xff1a;CodeTop&#xff0c;筛选条件为&#xff1a;目标公…...

编程日记 2023/9/8 19:46:26

lintcode 1446 · 01矩阵走路问题 【两次BFS, VIP 中等 1也计算距离，但是不入队列】

题目链接&#xff0c;描述 https://www.lintcode.com/problem/1446 给定一个大小为 n*m 的 01 矩阵 grid &#xff0c;1 是墙&#xff0c;0 是路&#xff0c;你现在可以把 grid 中的一个 1 变成 0&#xff0c;请问从左上角走到右下角是否有路可走&#xff1f;如果有路可走&am…...

编程日记 2023/9/8 19:45:25

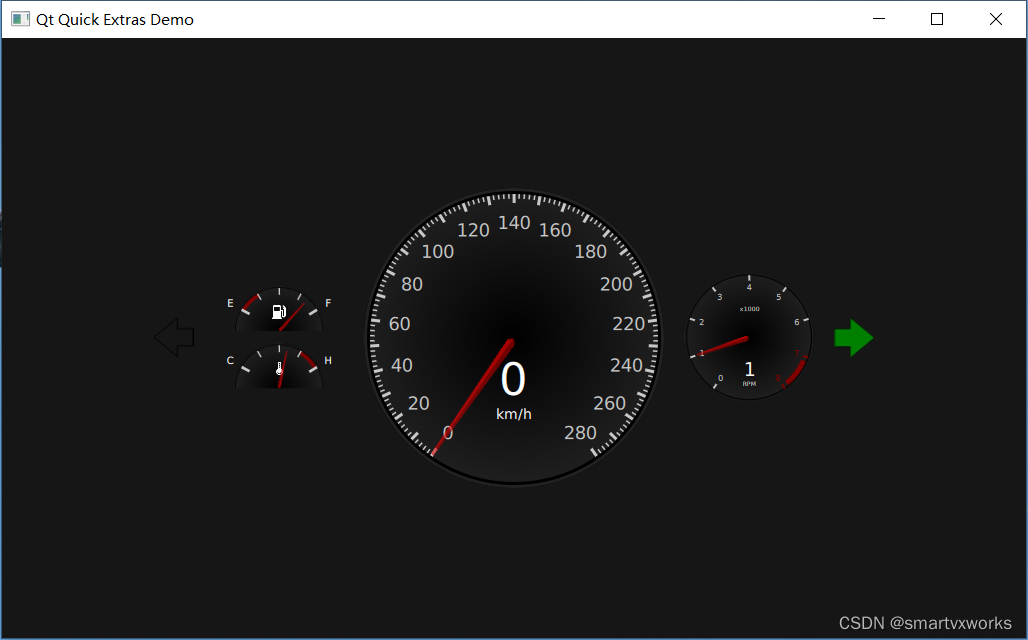
第一个实例：QT实现汽车电子仪表盘

目录 1.实现效果 1.1.视频演示 1.2.实现效果截图 2.生成的安装程序 3.功能概述 4.具体实现 5.QT扩展介绍 5.1.QT介绍 5.2.QT历史发展 5.3.QT平台支持 5.4.Qt Creator 5.5.优势 5.5.1.优良的跨平台特性 5.5.2.面向对象 5.5.3.丰富的 API 1.实现效果 1.1.视频演…...

编程日记 2023/9/8 19:44:24

【MySQL系列】MySQL的事务管理的学习（一）_ 事务概念 | 事务操作方式 | 事务隔离级别

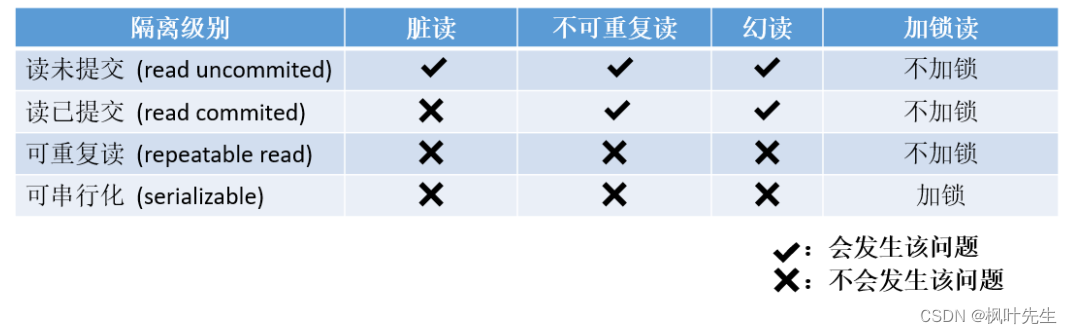
「前言」文章内容大致是MySQL事务管理。 「归属专栏」MySQL 「主页链接」个人主页 「笔者」枫叶先生(fy) 目录 一、事务概念二、事务的版本支持三、事务提交方式四、事务常见的操作方式4.1 事务正常操作4.2 事务异常验证 五、事务隔离级别5.1 查看与设置隔离性5.2 读未提交&…...

编程日记 2023/9/8 19:43:23

Java如何权衡是使用无序的数组还是有序的数组

在 Java 中，选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南： ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

编程新知 2025/8/3 11:17:37

视频字幕质量评估的大规模细粒度基准

大家读完觉得有帮助记得关注和点赞&#xff01;&#xff01;&#xff01; 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用&#xff0c;因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型&#xff08;VLMs&#xff09;在字幕生成方面…...

编程新知 2026/2/6 9:24:15

ETLCloud可能遇到的问题有哪些？常见坑位解析

数据集成平台ETLCloud&#xff0c;主要用于支持数据的抽取&#xff08;Extract&#xff09;、转换&#xff08;Transform&#xff09;和加载&#xff08;Load&#xff09;过程。提供了一个简洁直观的界面&#xff0c;以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

编程新知 2026/2/3 12:56:31

LabVIEW双光子成像系统技术

双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制&#xff0c;展现出显著的技术优势&#xff1a; 深层组织穿透能力&#xff1a;适用于活体组织深度成像 高分辨率观测性能&#xff1a;满足微观结构的精细研究需求 低光毒性特点&#xff1a;减少对样本的损伤…...

编程新知 2026/1/31 13:04:44

消防一体化安全管控平台：构建消防“一张图”和APP统一管理

在城市的某个角落&#xff0c;一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延&#xff0c;滚滚浓烟弥漫开来&#xff0c;周围群众的生命财产安全受到严重威胁。就在这千钧一发之际&#xff0c;消防救援队伍迅速行动&#xff0c;而豪越科技消防一体化安全管控平台构建的消防“…...

编程新知 2026/2/6 5:47:08

第一篇：Liunx环境下搭建PaddlePaddle 3.0基础环境（Liunx Centos8.5安装Python3.10+pip3.10）

第一篇&#xff1a;Liunx环境下搭建PaddlePaddle 3.0基础环境&#xff08;Liunx Centos8.5安装Python3.10pip3.10&#xff09; 一&#xff1a;前言二&#xff1a;安装编译依赖二&#xff1a;安装Python3.10三&#xff1a;安装PIP3.10四&#xff1a;安装Paddlepaddle基础框架4.1…...

编程新知 2026/1/31 20:22:32

车载诊断架构 --- ZEVonUDS（J1979-3）简介第一篇

我是穿拖鞋的汉子，魔都中坚持长期主义的汽车电子工程师。 老规矩，分享一段喜欢的文字，避免自己成为高知识低文化的工程师： 做到欲望极简，了解自己的真实欲望，不受外在潮流的影响，不盲从，不跟风。把自己的精力全部用在自己。一是去掉多余，凡事找规律，基础是诚信；二是…...

编程新知 2026/1/26 21:09:29

C++--string的模拟实现

一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现&#xff0c;其目的是加强对string的底层了解&#xff0c;以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量&#xff0c;…...

编程新知 2026/1/26 19:02:17

用神经网络读懂你的“心情”：揭秘情绪识别系统背后的AI魔法

用神经网络读懂你的“心情”：揭秘情绪识别系统背后的AI魔法 大家好，我是Echo_Wish。最近刷短视频、看直播，有没有发现，越来越多的应用都开始“懂你”了——它们能感知你的情绪，推荐更合适的内容，甚至帮客服识别用户情绪，提升服务体验。这背后，神经网络在悄悄发力，撑起…...

编程新知 2025/12/18 22:11:53

Python第七周作业

Python第七周作业 文章目录 Python第七周作业 1.使用open以只读模式打开文件data.txt&#xff0c;并逐行打印内容 2.使用pathlib模块获取当前脚本的绝对路径&#xff0c;并创建logs目录&#xff08;若不存在&#xff09; 3.递归遍历目录data&#xff0c;输出所有.csv文件的路径…...

编程新知 2025/12/14 13:20:23