当前位置： 首页 > news >正文

OpenPCDet系列 | 8.4 nuScenes数据集数据调用和数据分析

news 2026/2/7 14:42:19

文章目录

  • 1. 对数据集遍历
    • 1.1 统计mini版本的nuScenes各模态数据和关键帧的数量
    • 1.2 单独遍历lidar模态数据
    • 1.3 遍历scene统计数据
    • 1.4 遍历sample统计数据
    • 1.5 遍历sample_data统计数据
    • 1.6 数据集的底层结构
  • 2. 对数据集可视化
    • 2.1 render_sample和render_sample_data
    • 2.2 nusc.render_pointcloud_in_image
    • 2.3 nusc.render_annotation
    • 2.4 nusc.render_scene和nusc.render_scene_channel
    • 2.5 nusc.render_egoposes_on_map

相关文章：

OpenPCDet系列 | 8.4 nuScenes数据集数据调用和数据分析

文章目录 1. 对数据集遍历1.1 统计mini版本的nuScenes各模态数据和关键帧的数量1.2 单独遍历lidar模态数据1.3 遍历scene统计数据1.4 遍历sample统计数据1.5 遍历sample_data统计数据1.6 数据集的底层结构2. 对数据集可视化2.1 render_sample和render_sample_data2.2 nusc.rend…...

编程日记 2023/9/8 20:19:11

WeiTitlePopupWindow

目录 1 WeiTitlePopupWindow 1.1 // 设置可点击 1.2 // 设置弹窗外可点击 1.3 // 设置弹窗宽度和高度 1.4 // 设置弹窗布局界面 WeiTitlePopupWindow // 设置可点击setTouchable(true);...

编程日记 2023/9/8 20:18:10

qemu/kvm学习笔记

qemu/kvm架构 cpu虚拟化的示例 Reference: kvmtest.c [LWN.net] 主要步骤： QEMU通过/dev/kvm设备文件发起KVM_CREATE_VM ioctl，请求KVM创建一个虚拟机。KVM创建虚拟机相应的结构体，并为QEMU返回一个虚拟机文件描述符QEMU通过虚拟机文件描述…...

编程日记 2023/9/8 20:17:09

android 车载widget小部件部分详细源码实战开发-千里马车载车机framework开发实战课程

官网参考链接：https://developer.android.google.cn/develop/ui/views/appwidgets/overview 1、什么是小部件 App widgets are miniature application views that can be embedded in other applications (such as the home screen) and receive periodic updates…...

编程日记 2023/9/8 20:16:07

如何使用CSS画一个三角形

原理&#xff1a;其实就是规定元素的四个边框颜色及边框宽度&#xff0c;将元素宽高设置为0。如果要哪个方向的三角形&#xff0c;将对应其他三个方向的边框宽和颜色设置为0和透明transparent即可 1.元素设置边框&#xff0c;宽高&#xff0c;背景色 <style>.border {w…...

编程日记 2023/9/8 20:15:05

第15章_锁: (表级锁、页级锁、行锁、悲观锁、乐观锁、全局锁、死锁)

3.2 从数据操作的粒度划分&#xff1a;表级锁、页级锁、行锁 为了提高数据库并发度&#xff0c;每次锁定的数据范围越小越好&#xff0c;理论上每次只锁定当前操作的数据的方案会得到最大的并发度&#xff0c;但管理锁是很耗资源&#xff08;涉及获取、检查、释放锁等动作)。因…...

编程日记 2023/9/8 20:14:05

python音频转文字调用baidu

python音频转文字调用的是百度智能云的接口&#xff0c;因业务需求会涉及比较多数字&#xff0c;所以这里做了数字的处理&#xff0c;可根据自己的需求修改。 from flask import Flask, request, jsonify import requestsfrom flask_limiter import Limiterapp Flask(__name_…...

编程日记 2023/9/8 20:13:04

靶场溯源第二题

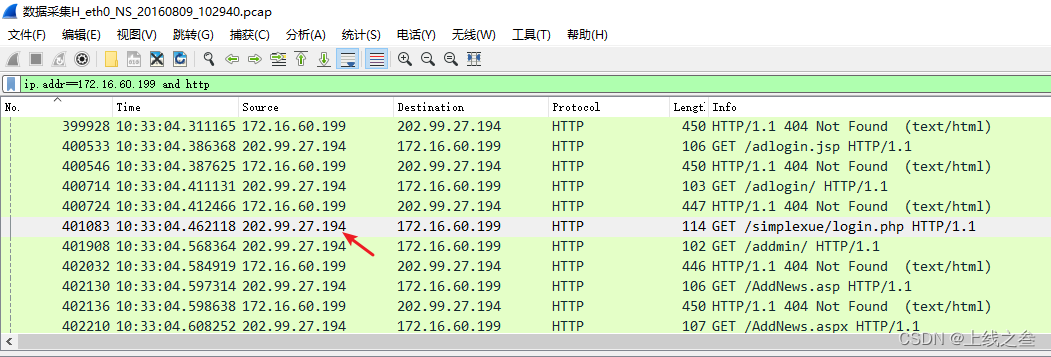
关卡描述&#xff1a;1. 网站后台登陆地址是多少&#xff1f;&#xff08;相对路径&#xff09; 首先这种确定的网站访问的都是http或者https协议&#xff0c;搜索http看看。关于http的就这两个信息&#xff0c;然后172.16.60.199出现最多&#xff0c;先过滤这个ip看看 这个很…...

编程日记 2023/9/8 20:12:01

mysql 的增删改查以及模糊查询、字符集语句的使用

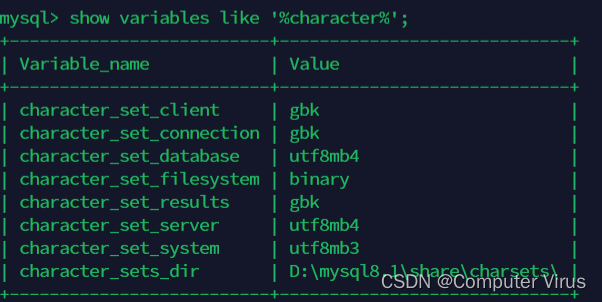
一、mysql启动与登陆(windows下的mysql操作) 1.启动mysql服务 net start mysql81 2.登陆mysql mysql -uroot -p 3.查看所有数据库 show databases; 二、模糊查询&#xff08;like&#xff09; 1. _代表查询单个 2.%代表查询多个 3.查找所有含有schema的数据库&#xff1b;…...

编程日记 2023/9/8 20:11:00

Python Django框架中文教程：学习简单、灵活、高效的Web应用程序框架

概述: Python Django是一种流行的Web应用程序框架&#xff0c;被广泛应用于开发高效、可扩展的网站和Web应用程序。Django以其简单、灵活和高效而受到开发者们的青睐。它提供了强大的工具和功能&#xff0c;使开发过程更加容易和高效。 Django的主要目标是帮助开发者快速构建…...

编程日记 2023/9/8 20:09:59

Docker认识即安装

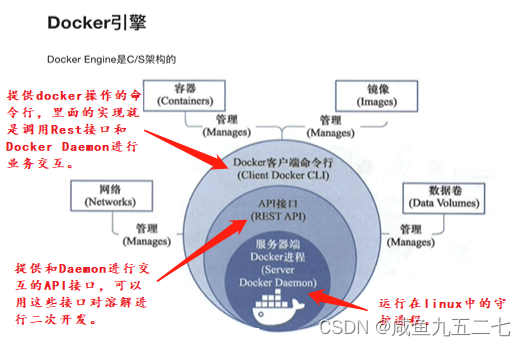
Docker及相关概念 Docker和虚拟机方式的区别&#xff1a;虚拟机技术是虚拟出一套硬件后&#xff0c;在其上运行一个完整的操作系统&#xff0c;在该系统上在运行所需应用进程&#xff1b;而容器内的应用进程是直接运行于宿主的内核&#xff0c;容器内没有自己的内核&#xff0…...

编程日记 2023/9/8 20:08:58

chrome 谷歌浏览器 导出插件拓展和导入插件拓展

给同事部署 微软 RPA时&#xff0c;需要用到对应的chrome浏览器插件&#xff1b;谷歌浏览器没有外网是不能直接下载拓展弄了半小时后才弄好&#xff0c;竟发现没有现成的教程&#xff0c;遂补充&#xff1b; 如何打包导出 谷歌浏览器 地址栏敲 chrome://extensions/在对应的地…...

编程日记 2023/9/8 20:07:54

fastjson漏洞批量检测工具

JsonExp 简介 版本&#xff1a;1.3.5 1. 根据现有payload&#xff0c;检测目标是否存在fastjson或jackson漏洞&#xff08;工具仅用于检测漏洞&#xff09;2. 若存在漏洞&#xff0c;可根据对应payload进行后渗透利用3. 若出现新的漏洞时&#xff0c;可将最新的payload新增至…...

编程日记 2023/9/8 20:06:53

Vue进阶（六十七）页面刷新路由传参丢失问题分析及解决

文章目录 一、前言二、问题排查三、延伸阅读3.1 Apache服务器access_log日志3.2 浏览器的常见User Agent 各字段的解释 一、前言 问题描述&#xff1a;Vue项目上线后&#xff0c;在IE浏览器上&#xff0c;从A页面跳转至B页面&#xff0c;B页面通过data中接收来自A页面的参数信…...

编程日记 2023/9/8 20:05:52

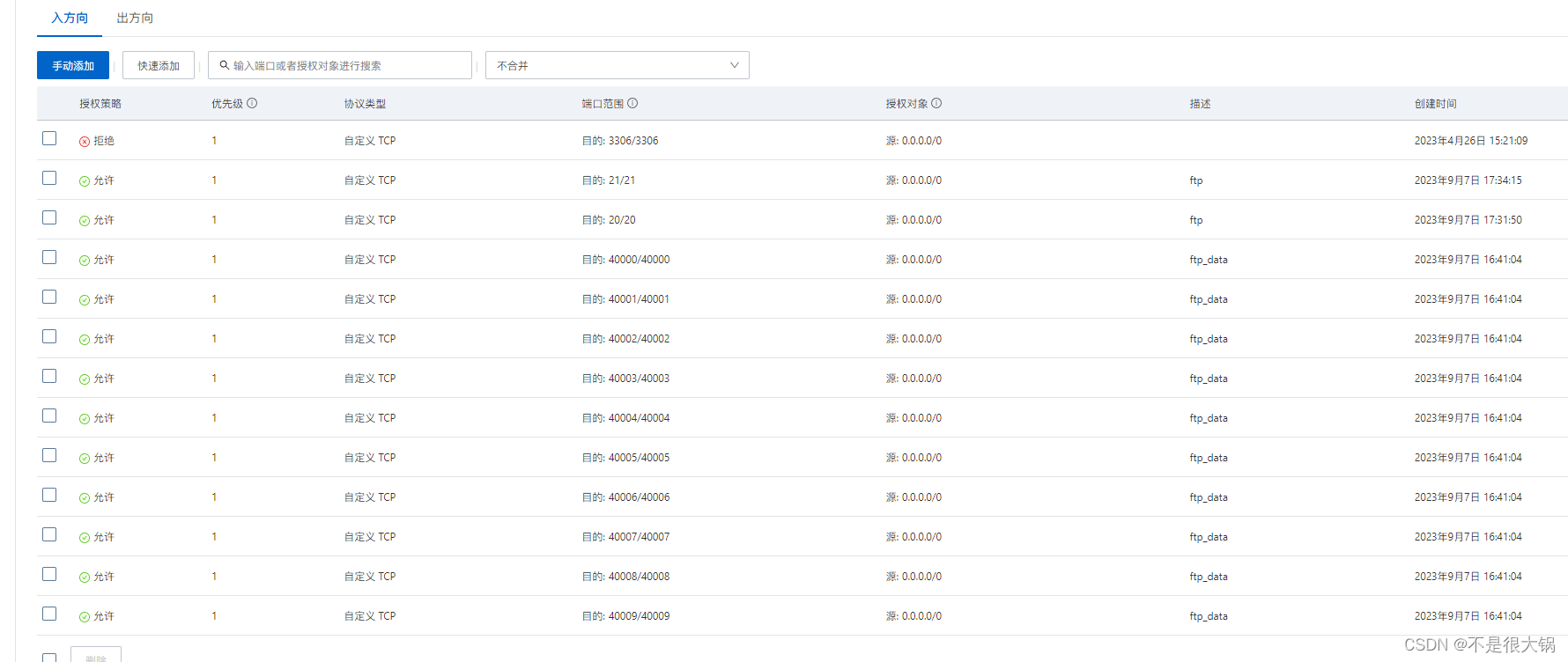
阿里云ubuntu服务器搭建ftp服务器

阿里云ubuntu服务器搭建ftp服务器 服务器环境安装步骤一.创建用户二.安装 vsftp三 配置vsftp四.配置阿里云安全组 服务器环境 阿里云上的云服务器&#xff0c;操作系统为 ubuntu20.04。 安装步骤 一.创建用户 为什么需要创建用户&#xff1f; 这里的用户&#xff0c;指的是…...

编程日记 2023/9/8 20:04:51

03 卷积操作图片

一、均值滤波 # 卷积操作 # 输入图片. input, 必须是4维tensor(图片数量, 图片高度, 图片的宽度, 图片的通道数) # filters, 卷积核, 必须是4维的tensor(卷积核的高度和宽度, 输入图片的通道数, 卷积核的个数) # strides, 步长, 卷积核在图片的各个维度上的移动步长, (1, 1, 1,…...

编程日记 2023/9/8 20:03:49

软考：中级软件设计师:程序语言基础：表达式，标准分类，法律法规，程序语言特点，函数传值传址

软考&#xff1a;中级软件设计师:程序语言基础&#xff1a;表达式 提示&#xff1a;系列被面试官问的问题&#xff0c;我自己当时不会&#xff0c;所以下来自己复盘一下&#xff0c;认真学习和总结&#xff0c;以应对未来更多的可能性 关于互联网大厂的笔试面试&#xff0c;都…...

编程日记 2023/9/8 20:02:49

Java“牵手”1688商品详情数据，1688商品详情API接口，1688API接口申请指南

1688平台商品详情接口是开放平台提供的一种API接口&#xff0c;通过调用API接口&#xff0c;开发者可以获取1688商品的标题、价格、库存、月销量、总销量、库存、详情描述、图片等详细信息 。 获取商品详情接口API是一种用于获取电商平台上商品详情数据的接口&#xff0c;通过…...

编程日记 2023/9/8 20:01:48

stable diffusion实践操作-批次出图

系列文章目录 stable diffusion实践操作 文章目录 系列文章目录前言一、批次出图介绍1.1 webUI设置1.2 参数介绍 二、批次出图使用2.1 如何设置2.1 效果展示 总结 前言 本章主要介绍SD批次出图。 想要一次产生多张图片的时候使用。 一、批次出图介绍 1.1 webUI设置 1.2 参数…...

编程日记 2023/9/8 20:00:47

LeetCode热题100 【cpp】题解（一）哈希表和双指针

文章目录 1. 两数之和49. 字母异位词分组128. 最长连续序列283. 移动零11. 盛最多水的容器15. 三数之和42. 接雨水 题单链接&#xff1a; LeetCode 热题 100 1. 两数之和 leetcode题目链接 题解1&#xff1a;暴力枚举 时间复杂度&#xff1a; O ( n 2 ) O(n^2) O(n2) class …...

编程日记 2023/9/8 19:59:44

生成 Git SSH 证书

&#x1f511; 1. ​​生成 SSH 密钥对​​ 在终端&#xff08;Windows 使用 Git Bash&#xff0c;Mac/Linux 使用 Terminal&#xff09;执行命令&#xff1a; ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" ​​参数说明​​&#xff1a; -t rsa&#x…...

编程新知 2025/9/18 11:31:13

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)

文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

编程新知 2026/1/31 23:44:39

Unity | AmplifyShaderEditor插件基础（第七集：平面波动shader）

目录 一、&#x1f44b;&#x1f3fb;前言 二、&#x1f608;sinx波动的基本原理 三、&#x1f608;波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、&#x1f30a;波动优化…...

编程新知 2026/2/6 22:55:12

人机融合智能 | “人智交互”跨学科新领域

本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

编程新知 2026/1/25 13:33:35

音视频——I2S 协议详解

I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议&#xff0c;专门用于在数字音频设备之间传输数字音频数据。它由飞利浦&#xff08;Philips&#xff09;公司开发&#xff0c;以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

编程新知 2026/2/1 2:08:53

GruntJS-前端自动化任务运行器从入门到实战

Grunt 完全指南&#xff1a;从入门到实战 一、Grunt 是什么&#xff1f; Grunt是一个基于 Node.js 的前端自动化任务运行器&#xff0c;主要用于自动化执行项目开发中重复性高的任务&#xff0c;例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

编程新知 2026/1/25 11:52:39

Python 训练营打卡 Day 47

注意力热力图可视化 在day 46代码的基础上&#xff0c;对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

编程新知 2025/11/24 9:42:16

c# 局部函数 定义、功能与示例

C# 局部函数&#xff1a;定义、功能与示例 1. 定义与功能 局部函数&#xff08;Local Function&#xff09;是嵌套在另一个方法内部的私有方法&#xff0c;仅在包含它的方法内可见。 • 作用&#xff1a;封装仅用于当前方法的逻辑&#xff0c;避免污染类作用域&#xff0c;提升…...

编程新知 2025/9/18 4:17:51

深度剖析 DeepSeek 开源模型部署与应用：策略、权衡与未来走向

在人工智能技术呈指数级发展的当下&#xff0c;大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性&#xff0c;吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型&#xff0c;成为释放其巨大潜力的关键所在&…...

编程新知 2025/12/27 19:12:07

数据结构：递归的种类（Types of Recursion）

目录 尾递归&#xff08;Tail Recursion&#xff09; 什么是 Loop&#xff08;循环&#xff09;&#xff1f; 复杂度分析 头递归&#xff08;Head Recursion&#xff09; 树形递归&#xff08;Tree Recursion&#xff09; 线性递归&#xff08;Linear Recursion&#xff09;…...

编程新知 2026/2/7 2:25:07