【二叉树】
1,利用类来构建结点,利用函数递归来构建树
2,因为左子树的结点编号是父节点的2倍,右子树的结点编号是父节点的2倍+1,所以可以用数组模拟建树的过程
构建二叉树
第一种构建方式
class treenode():#二叉树节点def __init__(self,val,lchild=None,rchild=None):self.val=val #二叉树的节点值self.lchild=lchild #左孩子self.rchild=rchild #右孩子def creat_tree(root,vals):if len(vals)==0:#终止条件:val用完了return rootif vals[0]!='#':#本层需要干的就是构建root、root.lchild、root.rchild三个节点。root = treenode(vals[0])vals.pop(0)root.lchild = creat_tree(root.lchild,val)root.rchild = creat_tree(root.rchild,val)return root#本次递归要返回给上一次的本层构造好的树的根节点else:root=Nonevals.pop(0)return root#本次递归要返回给上一次的本层构造好的树的根节点if __name__ == '__main__':root = Nonestrs="abc##d##e##"#前序遍历扩展的二叉树序列vals = list(strs)roots=creat_tree(root,vals)#roots就是我们要的二叉树的根节点。第二种构建方式
#存储结构的创建
class node:def __init__(self,data):self.data=data#数据域self.left=None#指向左子树根节点的指针self.right=None#指向右子树根节点的指针
root=None#如果根节点不存在l=[1,2,None,3,5,2,1]#假设题目给出列表形式的二叉树各节点数据
def newNode(input_list=[]):#创建二叉树,即二叉树插入if input_list is None or len(input_list)==0:#如果列表为空return Nonedata=input_list.pop(0)#取出并删除“当前”列表第一个数据if data is None:#到达空树,递归边界return Noneroot=node(data)#将该数据设置为根节点的数据,并创建此根节点的存储地址。root.left=newNode(input_list)#该根节点的左节点为“当前”列表的第二个数据root.right=newNode(input_list)#该根节点的右节点为“当前”列表的第三个数据#左右节点的递归顺序要根据题目给出的前中后层序排序改变。当前为前序遍历插入#中序遍历插入# root.left=newNode(input_list)# root = node(data)# root.right=newNode(input_list)#后序遍历插入# root.left=newNode(input_list)# root.right=newNode(input_list)# root=node(data)#层序遍历插入return root
newNode(l)二叉树的四种遍历
#二叉树遍历
#前序遍历
#root是构建二叉树后得到的根结点
def preorder(root):if root==None:return#到达空树,递归边界print(root.data)#访问根节点preorder(root.left)#访问左子树preorder(root.right)#访问右子树
#中序遍历
def inorder(root):if root==None:return#到达空树,递归边界inorder(root.left) # 访问左子树print(root.data)#访问根节点inorder(root.right)#访问右子树
#后序遍历
def postorder(root):if root==None:return#到达空树,递归边界postorder(root.left)#访问左子树postorder(root.right)#访问右子树print(root.data) # 访问根节点
#层序遍历
from queue import Queue
def layerorder(root):q=Queue()#注意队列里是存地址q.put(root)#将根节点地址入队while not q.empty():newroot=q.get()#取出队首元素q.pop()print(newroot.data)#访问队首元素if newroot.left is not None:#左子树非空q.put(newroot.left)if newroot.right is not None:#右子树非空q.put(newroot.right)#二叉树结点的查找,修改
goaldata=10#目标数据
newdata=11#新的数据
def search(root,goaldata,newdata):#先传进根节点if root==None:returnif root.data==goaldata:root.data=newdata# 再依次传进左右子节点search(root.left,goaldata,newdata)#往左子树搜索xsearch(root.right,goaldata,newdata)#往右子树搜素x二叉树题目其一:已知两种遍历求其他所有遍历
结论:中序序列可以与先序序列、后序序列、层序序列中的任意一个来构建唯一的二叉树,而后三者两两搭配或是三个一起上都无法构建唯一的二叉树。原因是先序、后序、层序均是提供根结点,作用是相同的,都必须由中序序列来区分出左右子树。
L2-006 树的遍历
已知中后求层序
class node:def __init__(self,data):self.data=dataself.left=Noneself.right=Nonen=int(input())
l1=list(map(int,input().split()))
l2=list(map(int,input().split()))def buildTree(inorder,postorder):def helper(in_left,in_right):if in_left>in_right:return Nonedata=postorder.pop()#后序排序从后依次弹出,遵循根右左,故一开始是根,之后一直右,然后左,如何判断该节点是左右,只需看in_left>in_right即可,一旦in_left<=in_right,说明右已经没有,开始进行左。root=node(data)index=idx_map[data]root.right = helper(index + 1, in_right)#为什么root.right必须放在root.left上面,在data是按后序排序逆序弹出#弹出根节点后就弹出右节点,这个时候如果先遍历左子树会找不到左子树的根节点root.left=helper(in_left,index-1)return rootidx_map={val:idx for idx,val in enumerate(inorder)}#将中序列表的值和下标对应return helper(0,len(inorder)-1)
p=buildTree(l2,l1)#得到的是一堆root数据结构的首地址,也就是二叉树根节点的地址
# print(p)
q=[p]#将首地址放到列表结构中
# print(q.pop(0))
res=[]
while(len(q)!=0):m=q.pop(0)#取出首地址if m!=None:res.append(m.data)if m.left!=None:q.append(m.left)if m.right!=None:q.append(m.right)
print(*res)L2-011 玩转二叉树
已知前中镜像翻转后求层
前序遍历倒过来就是后序遍历的镜像
from queue import Queue
n=int(input())
zx=list(map(int,input().split()))
qx=list(map(int,input().split()))class node():def __init__(self,data):self.data=dataself.left=Noneself.right=None
idx_map={val:i for i,val in enumerate(zx)}
def coms(inl,inr):if inl>inr:return Nonedata=qx.pop(0)#在前序中找到根节点#前序排序从前依次弹出,遵循根左右,故一开始是根,之后一直左,然后左,如何判断该节点是左右,只需看in_left>in_right即可,一旦in_left<=in_right,说明左已经没有,开始进行右。index=idx_map[data]#利用根节点的值找到其下标root=node(data)#建立二叉树#再利用下标将其分开#l.append(data)前序遍历root.left = coms(inl, index - 1)#l.append(data)中序遍历root.right = coms(index + 1, inr)# l.append(data)后序遍历return rootp=coms(0,len(zx)-1)#得到的是一堆root数据结构的首地址,也就是二叉树根节点的地址
# print(p)
q=[p]#将首地址放到列表结构中
# print(q.pop(0))
res=[]
while(len(q)!=0):m=q.pop(0)#取出首地址if m!=None:res.append(m.data)if m.right!=None:q.append(m.right)if m.left!=None:q.append(m.left)
print(*res)from queue import Queue
n=int(input())
zx=list(map(int,input().split()))
qx=list(map(int,input().split()))class node():def __init__(self,data):self.data=dataself.left=Noneself.right=None
idx_map={val:i for i,val in enumerate(zx)}
def coms(inl,inr):if inl>inr:return Nonedata=qx.pop(0)#在前序中找到根节点index=idx_map[data]#利用根节点的值找到其下标root=node(data)#建立二叉树#再利用下标将其分开#l.append(data)前序遍历root.left = coms(inl, index - 1)#l.append(data)中序遍历root.right = coms(index + 1, inr)# l.append(data)后序遍历return root
l=[]
def level(node):queue=Queue()queue.put(node)while not queue.empty():node=queue.get()l.append(node.data)if node.right is not None:#先加入右节点,做镜像翻转queue.put(node.right)if node.left is not None:queue.put(node.left)
level(coms(0,len(zx)-1))
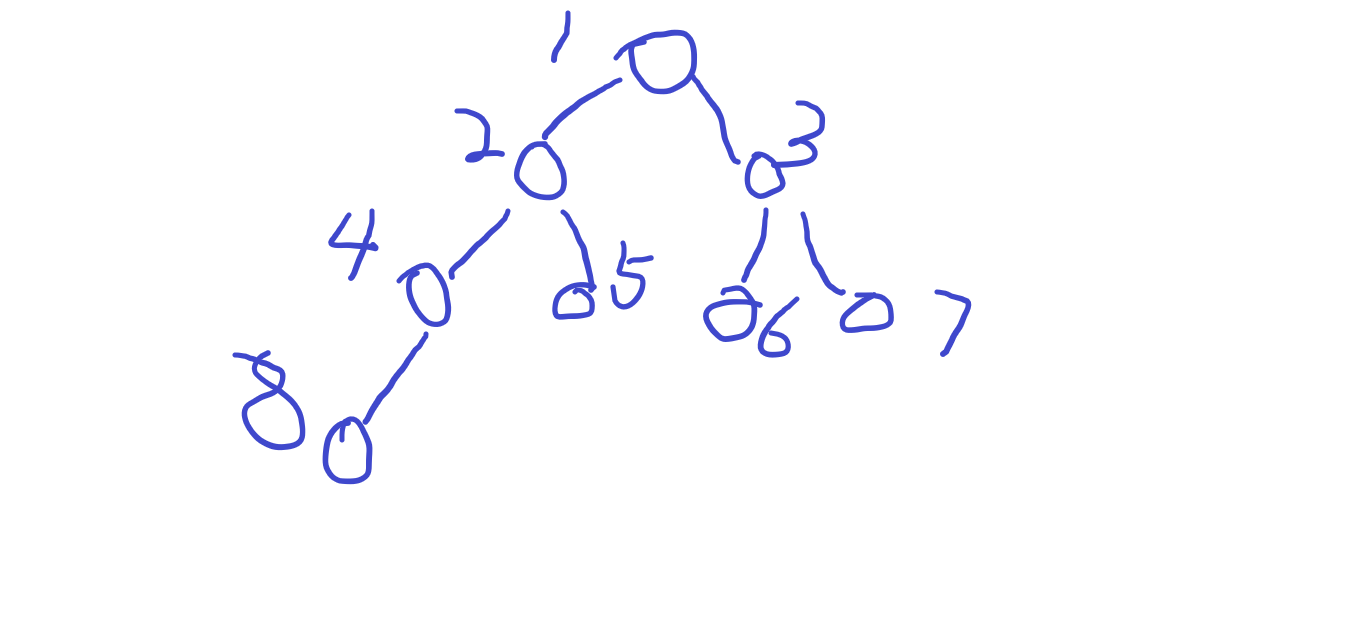
print(*l)L2-035 完全二叉树的层序遍历
由于树是递归实现的,后序排序符合递归顺序,而层序排序的顺序可以为我们提供每一次递归所满足的代数式。
n=int(input())
l=list(map(int,input().split()))
tree=[0]*n
def dfs(x):global indexif x>n:returndfs(x*2)dfs(x*2+1)tree[x-1]=l[index]index+=1
index=0
dfs(1)
print(*tree)二叉搜素树(BST)
二叉查找树一个实用的性质:对二叉查找树进行中序遍历,遍历的结果是有序的。
这是由于二叉查找树本身的定义中就包含了左子树<根结点<右子树的特点,而中序遍历的访问顺序也是左子树→根结点→右子树,因此,所得到的中序遍历序列是有序的。
# -*- coding:utf-8 -*-import sysreload(sys)
sys.setdefaultencoding('utf-8')class BSTNode:"""定义一个二叉树节点类。以讨论算法为主,忽略了一些诸如对数据类型进行判断的问题。"""def __init__(self, data, left=None, right=None):"""初始化:param data: 节点储存的数据:param left: 节点左子树:param right: 节点右子树"""self.data = dataself.left = leftself.right = rightclass BinarySortTree:"""基于BSTNode类的二叉排序树。维护一个根节点的指针。"""def __init__(self):self._root = Nonedef is_empty(self):return self._root is Nonedef search(self, key):"""关键码检索:param key: 关键码:return: 查询节点或None"""bt = self._rootwhile bt:entry = bt.dataif key < entry:bt = bt.leftelif key > entry:bt = bt.rightelse:return entryreturn Nonedef insert(self, key):"""插入操作:param key:关键码:return: 布尔值"""if self.is_empty():self._root = BSTNode(key)bt = self._rootwhile True:entry = bt.dataif key < entry:if bt.left is None:bt.left = BSTNode(key)bt = bt.leftelif key > entry:if bt.right is None:bt.right = BSTNode(key)bt = bt.rightelse:bt.data = keyreturndef delete(self, key):"""二叉排序树最复杂的方法:param key: 关键码:return: 布尔值"""p, q = None, self._root # 维持p为q的父节点,用于后面的链接操作if not q:print("空树!")returnwhile q and q.data != key:p = qif key < q.data:q = q.leftelse:q = q.rightif not q: # 当树中没有关键码key时,结束退出。return# 上面已将找到了要删除的节点,用q引用。而p则是q的父节点或者None(q为根节点时)。if not q.left:if p is None:self._root = q.rightelif q is p.left:p.left = q.rightelse:p.right = q.rightreturn# 查找节点q的左子树的最右节点,将q的右子树链接为该节点的右子树# 该方法可能会增大树的深度,效率并不算高。可以设计其它的方法。r = q.leftwhile r.right:r = r.rightr.right = q.rightif p is None:self._root = q.leftelif p.left is q:p.left = q.leftelse:p.right = q.leftdef _pre_order(self, node=None):if node is None:node = self._rootyield node.dataif node.left is not None:for item in self._pre_order(node.left):yield itemif node.right is not None:for item in self._pre_order(node.right):yield itemdef _mid_order(self, node=None):if node is None:node = self._rootif node.left is not None:for item in self._mid_order(node.left):yield itemyield node.dataif node.right is not None:for item in self._mid_order(node.right):yield itemdef _mid_order1(self):"""实现二叉树的中序遍历算法,展示我们创建的二叉排序树.直接使用python内置的列表作为一个栈。:return: data"""stack = []node = self._rootwhile node or stack:while node:stack.append(node)node = node.leftnode = stack.pop()yield node.datanode = node.rightdef _post_order(self, node=None):if node is None:node = self._rootif node.left is not None:for item in self._post_order(node.left):yield itemif node.right is not None:for item in self._post_order(node.right):yield itemyield node.datadef pre_order(self):return list(self._pre_order())def mid_order(self):return list(self._mid_order()) # return list(self._mid_order1())def post_order(self):return list(self._post_order())if __name__ == '__main__':lis = [62, 58, 88, 47, 73, 99, 35, 51, 93, 37]bs_tree = BinarySortTree()for i in range(len(lis)):bs_tree.insert(lis[i])print "先序遍历:", bs_tree.pre_order()print "中序遍历:", bs_tree.mid_order()print "后序遍历:", bs_tree.post_order()L3-010 是否完全二叉搜索树
因为左子树的结点编号是父节点的2倍,右子树的结点编号是父节点的2倍+1,所以可以用数组模拟建树的过程;
最后题目要求层序输出比较简单,直接按编号大小输出即可;
还有一问是判断该树是否为完全二叉树,完全二叉树的定义是若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,所以最后的结点编号肯定和n是相等的。
相关文章:

【二叉树】
1,利用类来构建结点,利用函数递归来构建树2,因为左子树的结点编号是父节点的2倍,右子树的结点编号是父节点的2倍1,所以可以用数组模拟建树的过程构建二叉树第一种构建方式class treenode():#二叉树节点def __init__(se…...

华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】
刷算法题之前必看 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD 清单查看地址:https://blog.csdn.net/hihell/category_12199283.html 华为OD详细说明:https://dream.blog.csdn.net/article/details/128980730 华为OD机试题…...

【设计模式】对象行为型模式
行为创建型模式 系列综述: 来源:该系列是主要参考《大话设计模式》和《设计模式(可复用面向对象软件的基础)》,其他详细知识点拷验来自于各大平台大佬的博客。 总结:汇总篇 如果对你有用,希望关注点赞收藏一波。 文章目…...
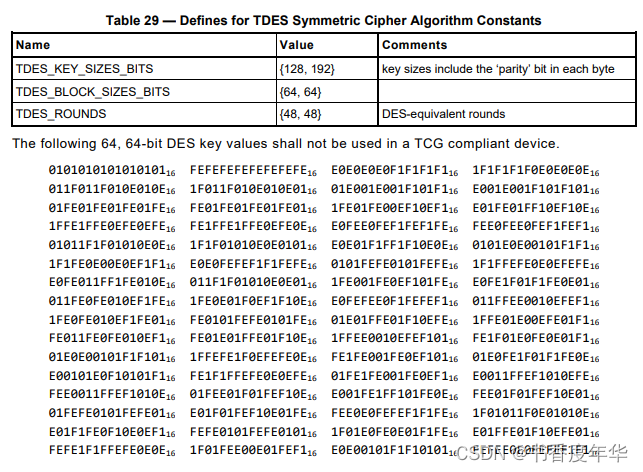
「TCG 规范解读」第11章 TPM工作组 TCG算法注册表
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alli…...

华为OD机试 - 事件推送(C++) | 附带编码思路 【2023】
刷算法题之前必看 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD 清单查看地址:https://blog.csdn.net/hihell/category_12199283.html 华为OD详细说明:https://dream.blog.csdn.net/article/details/128980730 华为OD机试题…...

Java ”框架 = 注解 + 反射 + 设计模式“ 之 注解详解
Java ”框架 注解 反射 设计模式“ 之 注解详解 每博一文案 刹那间我真想令时光停住,好让我回顾自己,回顾失去的年华,缅怀哪个穿一身短小的连衣裙 和瘦窄的短衫的小女孩。让我追悔少年时代,我心灵的愚钝无知,它轻易…...
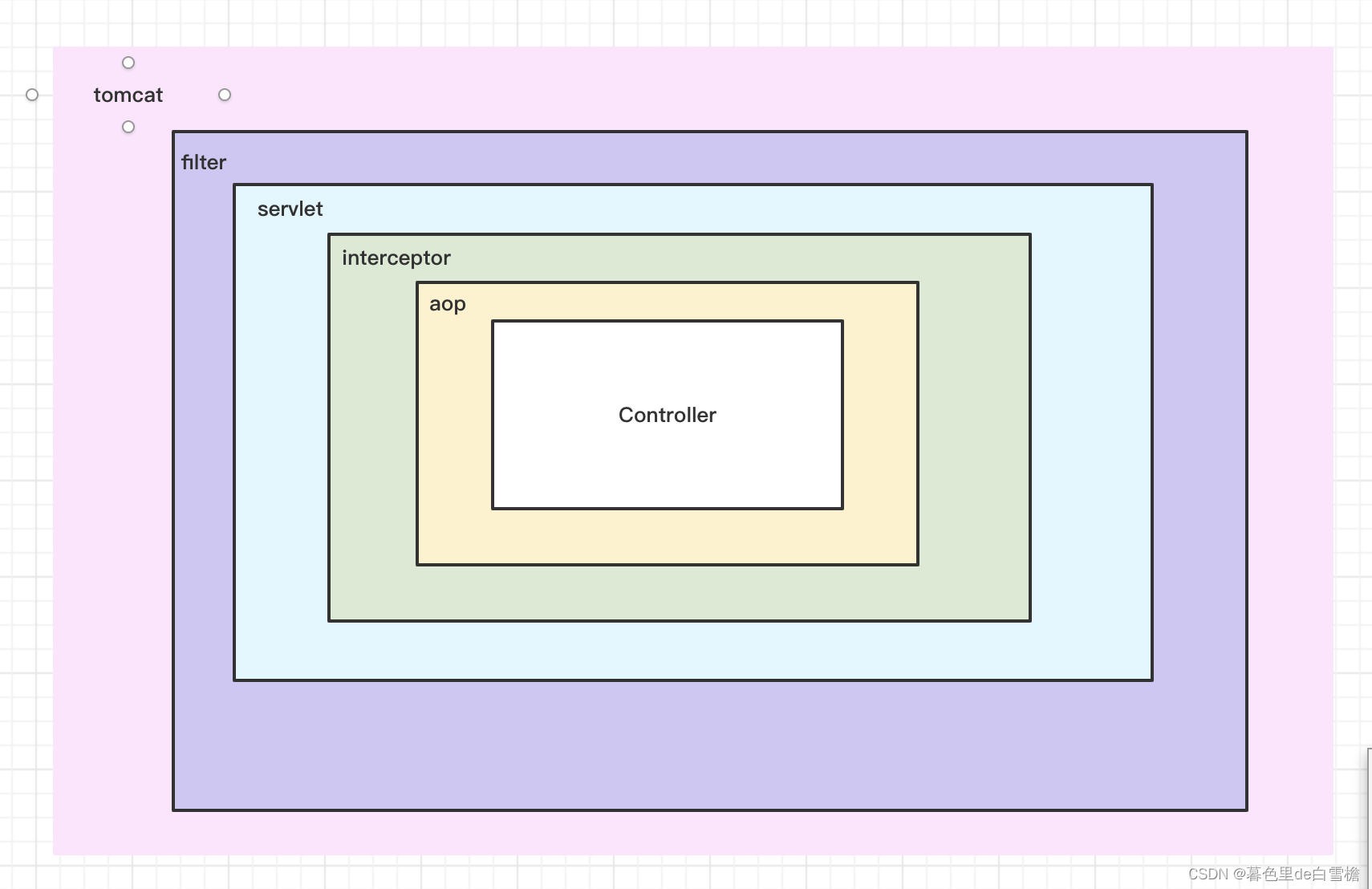
【拦截器、过滤器、springAop】那些不为人知的隐秘
首先说到这几个词的时候,大家肯定都很熟悉了,甚至觉得这几个的区别刚刚毕业都能回答了,但是我想大家在实际应用过程中是真得会真正的使用吗?换言之,什么时候用过滤器什么时候使用拦截器,什么时候使用spring…...

记录charles手机端配置https的成功过程
1.百度 https://www.likecs.com/show-204025787.html https://blog.csdn.net/enthan809882/article/details/117572094?spm1001.2101.3001.6650.6&utm_mediumdistribute.pc_relevant.none-task-blog-2defaultBlogCommendFromBaiduRate-6-117572094-blog-122959902.pc_rele…...
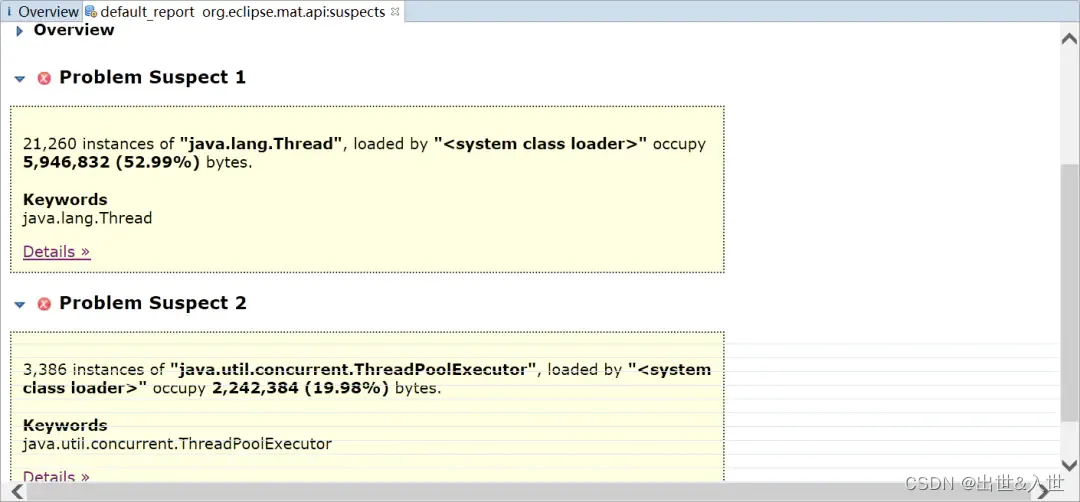
你知道这几种常见的JVM调优场景吗?
看此文前需已了解了运行时的数据区域和常用的垃圾回收算法,也了解了Hotspot支持的垃圾回收器。 一、cpu占用过高 cpu占用过高要分情况讨论,是不是业务上在搞活动,突然有大批的流量进来,而且活动结束后cpu占用率就下降了…...
)
华为OD机试真题Python实现【最长连续子串】真题+解题思路+代码(20222023)
最长连续子串 题目 给定一个字符串 只包含字母和数字 按要求找出字符串中的最长连续子串的长度 字符串本身是其最长的子串 子串要求 只包含一个字母(a~z A~Z)其余必须是数字字母可以在子串中的任意位置 如果找不到满足要求的子串 比如说,全是字母或数字则返回-1 🔥🔥🔥…...
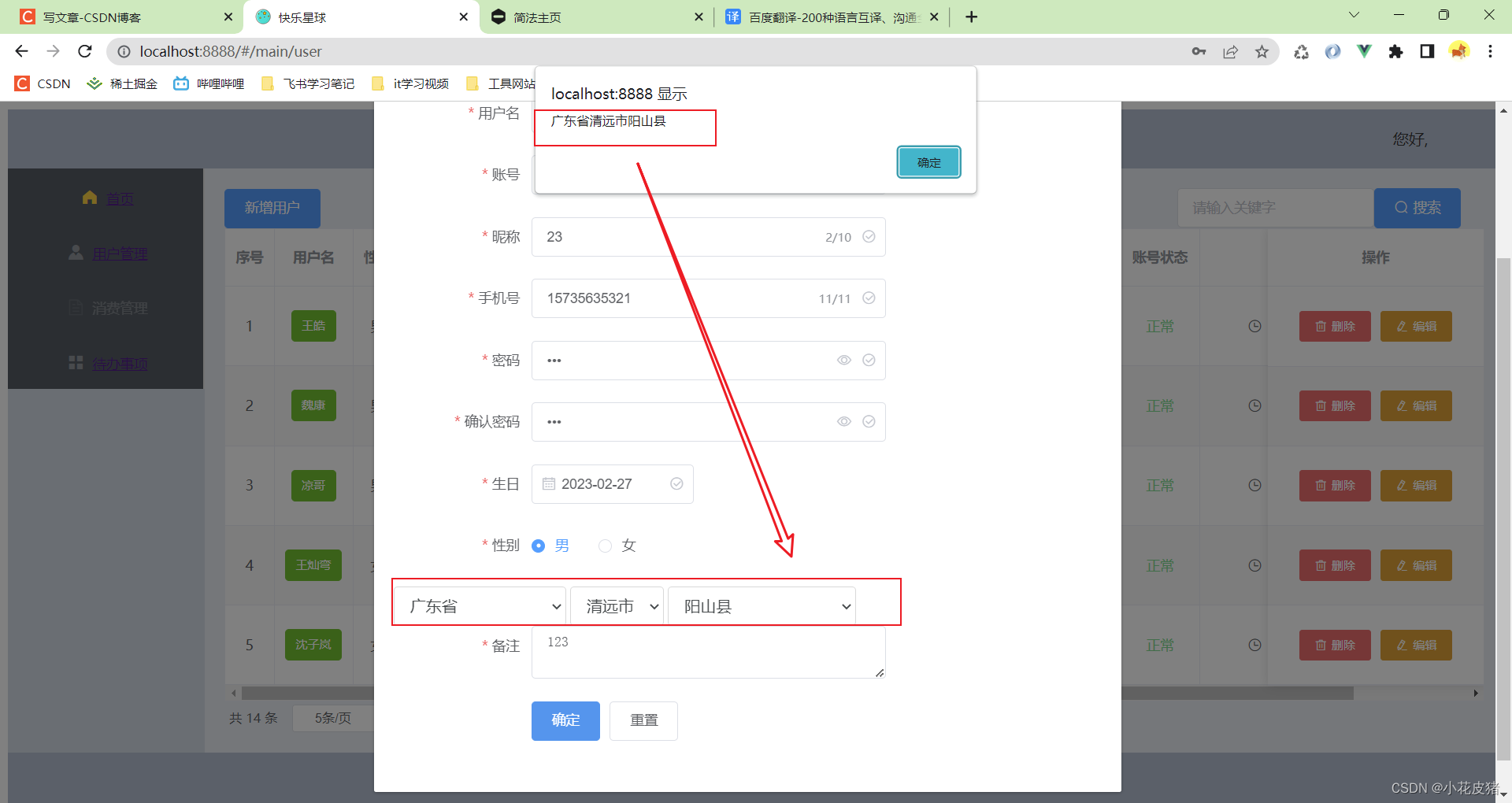
Vue使用distpicker插件实现省市级下拉框三级联动
前言 这几天做项目,想着用一个全国省市区插件,之前就知道有几种,比如通过JSON文件生成对应的区域下拉框,element-china-are插件,包括distpicker插件 今天主要介绍的是如何使用distpicker插件实现省市级三联跳动 官网…...

Unity Avatar Foot IK - Avatar Foot Placement Resolution
文章目录简介实现Avatar FBX Import SettingsAnimator SettingsOn Animator IKCalculate IK Position & RotationBody PositionApply IK Position & Rotation简介 通过Unity内部的Mecanim动画系统实现的FootIK功能,效果如图所示,左右分别为开启…...

是时候告别这些 Python 库了
随着每个 Python 版本的发布,都会添加新模块,并引入新的更好的做事方式,虽然我们都习惯了使用好的旧 Python 库和某些做事方式,但现在也时候升级并利用新的和改进的模块及其特性了。 文章目录技术提升PathlibSecretsZoneinfoDatac…...

nodejs基于vue论坛交流管理系统
可定制框架:ssm/Springboot/vue/python/PHP/小程序/安卓均可开发目录 目录 1 绪论 1 1.1课题背景 1 1.2课题研究现状 1 1.3初步设计方法与实施方案 2 1.4本文研究内容 2 2 系统开发环境 4 3 系统分析 6 3.1系统可行性分析 6 3.1.1经济可行性 6 3.1.2技术可行性 6 3.1.3运行可行…...
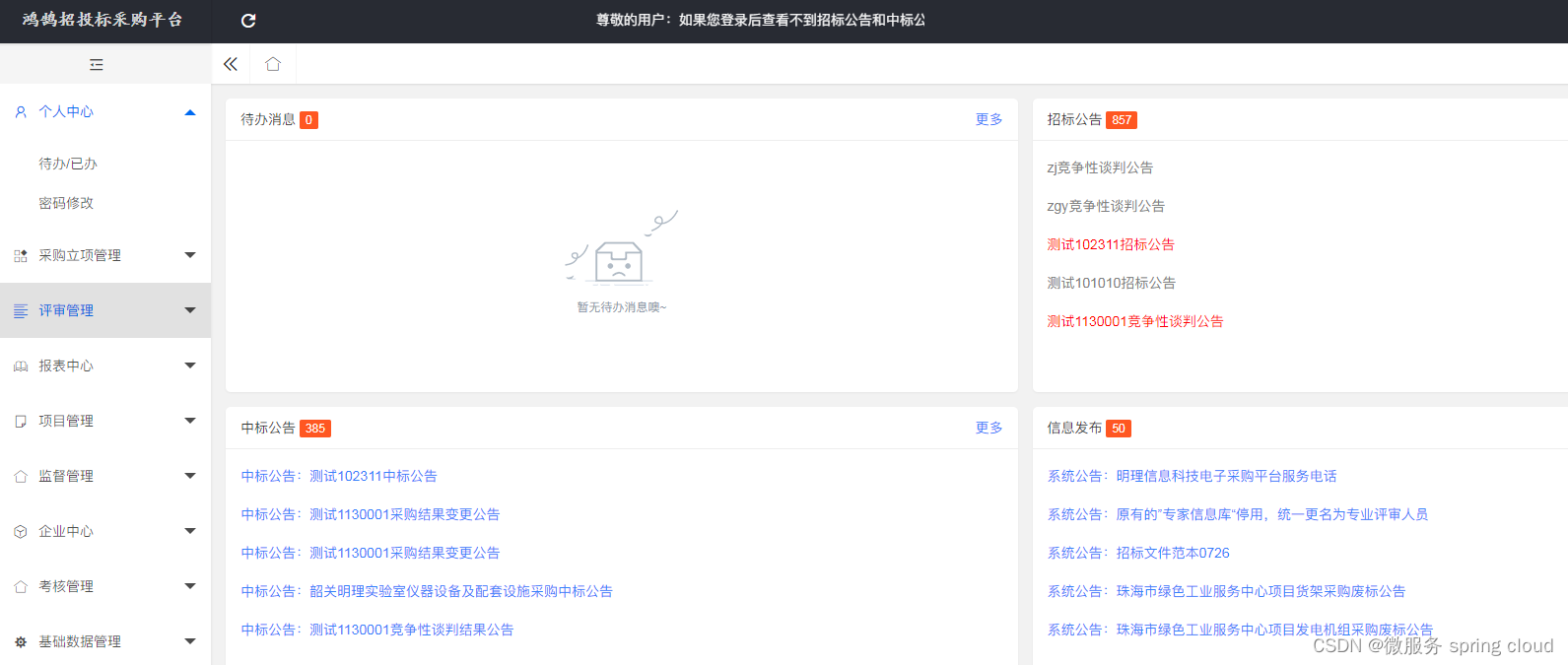
企业电子招投标采购系统源码之系统的首页设计
功能模块: 待办消息,招标公告,中标公告,信息发布 描述: 全过程数字化采购管理,打造从供应商管理到采购招投标、采购合同、采购执行的全过程数字化管理。通供应商门户具备内外协同的能力,为…...
)
华为OD机试真题Python实现【竖直四子棋】真题+解题思路+代码(20222023)
竖直四子棋 题目 竖直四子棋的棋盘是竖立起来的,双方轮流选择棋盘的一列下子, 棋子因重力落到棋盘底部或者其他棋子之上,当一列的棋子放满时,无法再在这列上下子。 一方的4个棋子横、竖或者斜方向连成一线时获胜。 现给定一个棋盘和红蓝对弈双方的下子步骤,判断红方或蓝…...

LeetCode 73. 矩阵置零
LeetCode 73. 矩阵置零 难度:middle\color{orange}{middle}middle 题目描述 给定一个 KaTeX parse error: Double subscript at position 3: _m_̲ x _n_ 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法…...
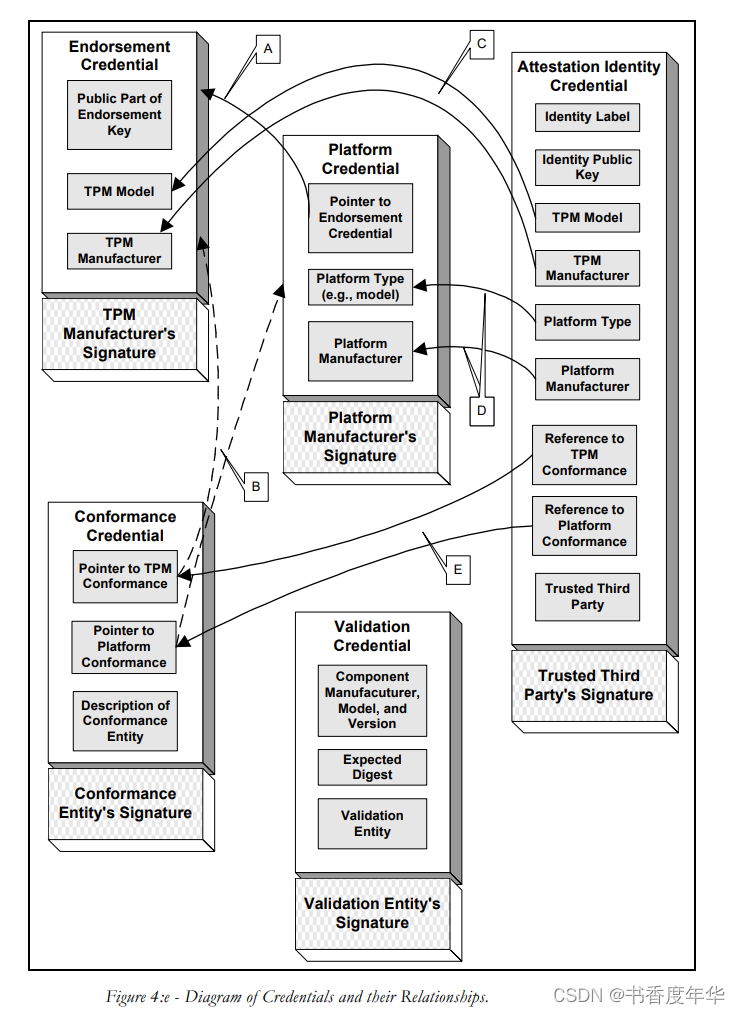
「TCG 规范解读」第10章 TPM工作组 保护你的数字环境
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alli…...
)
华为OD机试真题Python实现【 找字符】真题+解题思路+代码(20222023)
找字符 题目 给定两个字符串, 从字符串2中找出字符串1中的所有字符, 去重并按照 ASCII 码值从小到大排列。 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Python)真题目录汇总 ## 输入 字符范围满足 ASCII 编码要求, 输入字符串1长度不超过1024, 字符串…...
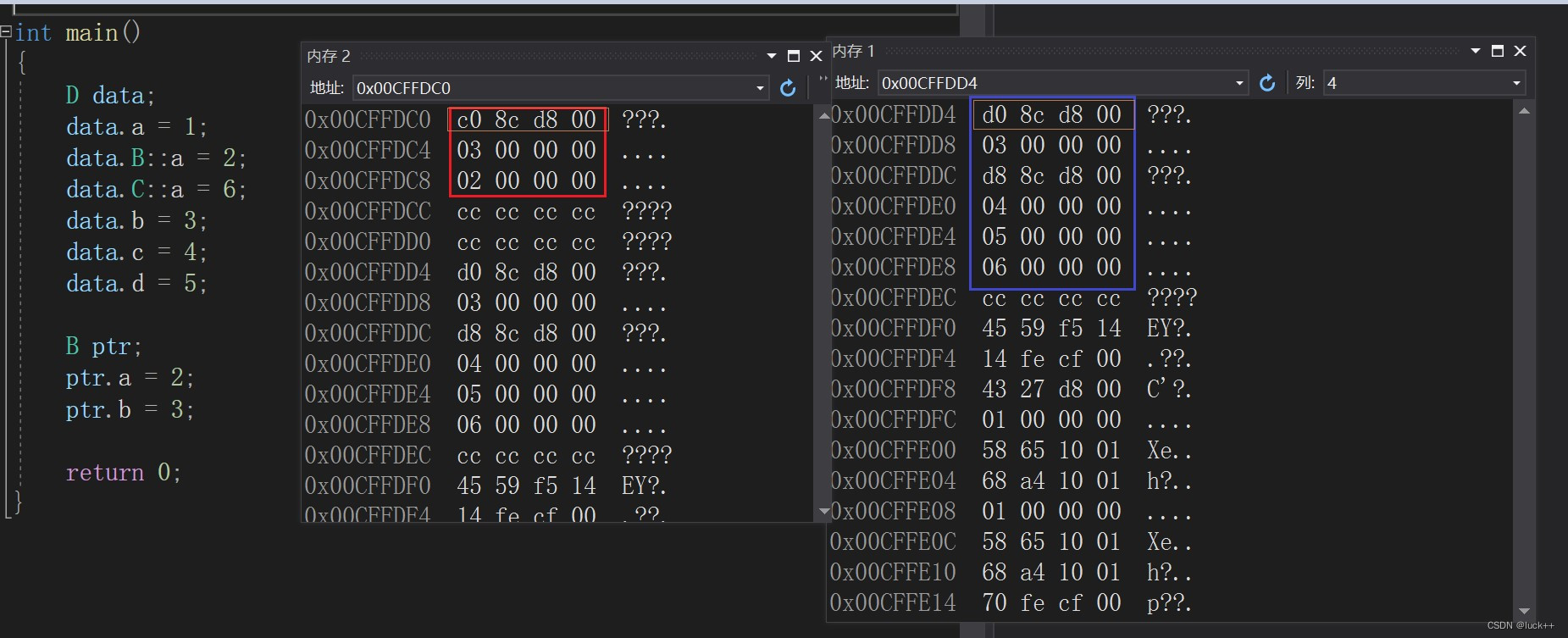
如何解决多继承下的 菱形继承 问题
目录 概念: 菱形虚拟继承: 概念: 此时D类属于多继承,可以看到D类里面会有两份A类的数据,菱形继承也并不一定就一定就是上图的菱形,假如B类下面还有一个类,D类继承它,同样也是菱形继承问题 cla…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...
