算法通关村第十八关:青铜挑战-回溯是怎么回事
青铜挑战-回溯是怎么回事
回溯,最重要的算法之一
主要解决一些暴力枚举也搞不定的问题,例如组合、分割、子集、排列、棋盘等
从性能角度来看回溯算法的效率并不高,但对于这些暴力都搞不定的算法能出结果就很好了,效率低点没关系
回溯可视为递归的拓展,很多思想和解法都与递归密切相关,对比递归来分析其特征会理解的更深刻
举例说明递归和回溯的区别:
设想一个场景,某猛男想脱单,两种策略:
- 递归策略:先与意中人制造偶遇,然后了解人家的情况,然后约人家吃饭,有好感之后尝试拉人家的手,没有拒绝就表白
- 回溯策略:先统计周围所有单身女孩,然后一个一个表白,被拒绝就说”我喝醉了“,然后就当啥也没有发生,继续下一个
回溯最大的好处:有非常明确的模板
所有的回溯都是一个大框架,因此透彻理解回溯的框架是解决一切回溯问题的基础
回溯不是万能的,解决的问题也是非常明确的,例如组合、分割、子集、排列、棋盘等
不过这些问题具体处理时又有很多不同
回溯可视为递归的拓展,代码结构特别像深度遍历N叉树
难点:回溯在递归语句之后有个”撤销“的操作。
好比谈了个新女朋友,来你家之前,要将前任的东西赶紧藏起来。回溯也一样,有些信息是前任的,要处理掉才能重新开始。
回溯的模板如下
void backtracking(参数){if(终止条件){存放结果;return;}for(选择本层集合中元素(画成树,就是树节点孩子的大小)){处理节点;backtracking(参数);回溯,撤销处理结果}
}
1. 从N叉树说起
二叉树的前序遍历
class TreeNode:def __init__(self, val):self.val = valself.left = Noneself.right = Nonedef tree_dfs(root):if root is None:returnprint(root.val)tree_dfs(root.left)tree_dfs(root.right)
N叉树的前序遍历
class TreeNode:def __init__(self, val):self.val = valself.children = []def tree_dfs(root):# 递归终止条件if root is None:return# 节点处理print(root.val)# 通过循环,分别遍历N个子树for i in root.children:tree_dfs(i)
回溯模板与N叉树的遍历模板非常像!!!
2. 为什么有的问题暴力枚举也不行
什么问题暴力枚举也不行?
举个例子:
LeetCode77 组合
https://leetcode.cn/problems/combinations/
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
n=4, k=2时,双层暴力枚举
def violent_enumeration():res = []for i in range(1, 5):for j in range(i + 1, 5):res.append((i, j))return resif __name__ == '__main__':print(violent_enumeration()) # [(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)]
n=10, k=3时,三层暴力枚举
def violent_enumeration():res = []for i in range(1, 11):for j in range(i + 1, 11):for k in range(j + 1, 11):res.append((i, j, k))return res
k未知时,循环次数未知,这时暴力枚举就失效了
这就是组合类型问题,除此之外,子集、排列、切割、棋盘等方面都有类似的问题,我们需要找到更好的方式
3. 回溯=递归+局部枚举+手动撤销(放下前任)
继续研究
LeetCode77 组合
https://leetcode.cn/problems/combinations/
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
n=4, k=2时

n=5, k=3时

从图中我们可以发现,元素个数n相当于树的宽度(横向),每个结果的元素个数k相当于树的深度(纵向)
此外还有一下规律
- 局部枚举:每次都是从类似 [1,2,3,4] 这样的序列进行枚举,越往后枚举范围越小
- 递归:再看n=5,k=3时图中红色大框部分,执行过程与n=4,k=2处理过程一直,时可以递归的子结构
- 手动撤销:观察图中可以看到,取3得到[1,2,3]之后,需要将3撤掉,再继续取4得到[1,2,4]
- 对应的代码操作:
- 将第一个结果放到 path中,path=[1]
- 将第二个结果放到 path中,path=[1,2]
- 将第三个结果放到 path中,path=[1,2,3]
- 将结果输出,撤销3, path=[1,2]
- 继续枚举,将第三个结果放到 path中,path=[1,2,4]
- …
综上,可以得到 回溯=递归+枚举+手动撤销
这就是回溯的基本规律,掌握之后就可写出完整的回溯代码了
回溯代码实现
import copyclass Solution:def combine(self, n: int, k: int) -> List[List[int]]:def dfs(k, n, begin, path, res):# 递归终止条件是:path的长度等于kif len(path) == k:res.append(copy.deepcopy(path))return# 枚举:针对一个节点,遍历可能的搜索起点for i in range(begin, n+1):# 像路径变量里添加一个数,就是树枝的值path.append(i)# 搜索起点加1,缩小范围,为下一轮递归做准备,因为不允许出现重复的元素dfs(k, n, i + 1, path, res)# 手动撤销path.pop()res = []if k <= 0 or n < k:return respath = []begin = 1dfs(k, n, begin, path, res)return res
4. 图解为什么有个撤销的操作
暂无,理解了上一小节的 手动撤销 即可
5. 回溯热身-再论二叉树的路径问题
5.1 输出二叉树的所有路径
LeetCode 257
https://leetcode.cn/problems/binary-tree-paths/
思路分析
方法1:深度优先搜索
深度优先搜索就是从根节点开始一直找到叶子结点,这里可以先判断当前节点是不是叶子结点,再决定是不是向下走,如果是叶子结点,我们就增加一条路径。这个之前学习,这里不再赘述
方法2:回溯
从回溯的角度分析,得到第一条路径ABD之后怎么找到第二条路径ABE,这里就是先将D撤销,然后再继续递归就可以了
难点,手动撤销
代码实现
方法1:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:def search_path(node, path):if not node:return path += str(node.val)if not node.left and not node.right:paths.append(path)else:path += "->"search_path(node.left, path)search_path(node.right, path)paths = []if root:search_path(root, path="")return paths方法2:回溯
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:def search_path(node, path, paths):if node is None:returnpath.append(str(node.val))if node.left is None and node.right is None:paths.append('->'.join(path))for i in [node.left, node.right]:search_path(i, path, paths)path.pop() # 返回上一层递归时,要让当前路径恢复原样paths = []path = []if root:search_path(root, path, paths)return paths
5.2 路径总和问题
LeetCode 113 路径总和 II
https://leetcode.cn/problems/path-sum-ii/
思路分析
目标:路径总和 targetSum=22
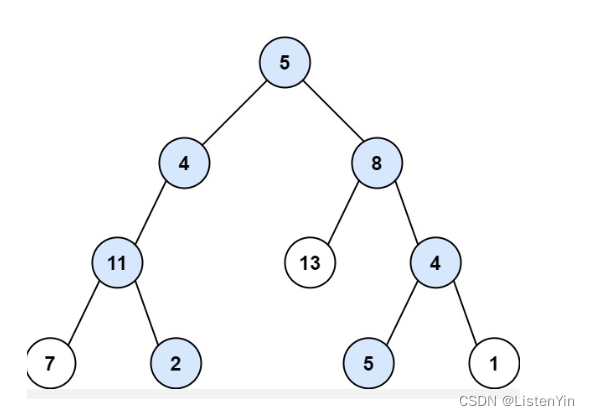
- 根节点5
- 需要左侧或右侧target_sum=22-5=17
- 继续看左子树node(4),需要node(4)左子树或右子树满足 target_sum=17-4=13
- 依次类推 … …
代码实现
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
import copyclass Solution:def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:def find(node, target_sum, path, paths):if node is None:returnpath.append(node.val)if node.left is None and node.right is None and node.val == target_sum:paths.append(copy.deepcopy(path))target_sum -= node.valfor i in [node.left, node.right]:find(i, target_sum, path, paths)path.pop()paths = []path = []if root:find(root, targetSum, path, paths)return paths注:不想用copy,也可以用 path[:] 替代
相关文章:

算法通关村第十八关:青铜挑战-回溯是怎么回事
青铜挑战-回溯是怎么回事 回溯,最重要的算法之一 主要解决一些暴力枚举也搞不定的问题,例如组合、分割、子集、排列、棋盘等 从性能角度来看回溯算法的效率并不高,但对于这些暴力都搞不定的算法能出结果就很好了,效率低点没关系…...

【Redis】深入探索 Redis 的数据类型 —— 字符串 string
文章目录 前言一、string 类型的操作命令设置和获取相关命令1. SET 和 GET2. MSET 和 MGET3. SETNX、SETEX、SETPX 计数相关命令1. INCR 和 INCRBY2. DECR 和 DECRBY3. INCRBYFLOAT 字符串操作相关命令1. APPEND2. GETRANGE3. SETRANGE4. STRLEN string 相关命令总结 二、strin…...

Linux操作命令笔记
Linux Linux的字母大小写下载和卸载软件更新查看空间使用情况当前目录所在的位置查看文件中的内容查看目录下的文件重启关机移动文件磁盘管理软件修改权限删除文件或文件夹新建文件夹移动一个文件夹文件重命名编译C和C文件VIM编辑器的相关操作 Linux的字母大小写 Linux的文件以…...

1.8 工程相关解析(各种文件,资源访问
目录 1.8 工程相关解析(各种文件,资源访问) 分类 Android 基础入门教程 本节引言: 1.工程项目结构解析: 1.res资源文件夹介绍: 2.如何去使用这些资源 2.深入了解三个文件: MainActivity.java: 布局…...

unity 前后左右 移动
using System.Collections; using System.Collections.Generic; using UnityEngine; public class NewBehaviourScript : MonoBehaviour { public float moveSpeed 5f; // 移动速度 public float rotateSpeed 180f; // 旋转速度 // Start is called before the firs…...

计算机视觉传统图像处理库opencv的使用
人工智能领域的图像处理分支,整理了计算机视觉传统图像处理库opencv的使用网址链接。 opencv使用范围,主要用在计算机视觉、视频分析、机器学习、医学影像处理、自动驾驶、工业检测、游戏开发上。 1):opencv效果视频 opencv10个应…...

【数据库】通过实例讲清楚,Mongodb的增删查改,分组查询,聚合查询aggregate
目录 一.基础概念 二.数据库的管理 1.创建数据库 2.删除数据库 二.集合的管理 1.显示所有集合 2.创建集合 3.删除当前集合 4.向集合中插入元素 三.文档的管理 1.文档插入 2.文档的更新 3.文档的删除 4.文档查询 (1)查询基本语法࿱…...
)
vue + video.js 加载多种视频流(HLS、FLV、RTMP、RTSP)
起因: 由于需要在一个项目内接入多种常用的视频流,所以接触到video.js,这里就做个记录。 框架: vue2 video.js videojs-contrib-hls videojs-flvjs-es6 videojs-flash video-js.swf vue安装就不讲了,直接从项目…...

用 Python 微调 ChatGPT (GPT-3.5 Turbo)
用 Python 微调 ChatGPT (GPT-3.5 Turbo) 备受期待的 GPT-3.5 Turbo 微调功能现已推出,并且为今年秋季即将发布的 GPT-4 微调功能奠定了基础。 这不仅仅是一次简单的更新——它是一个游戏规则改变者,为开发人员提供了完美定制人工智能模型的关键解决方案…...
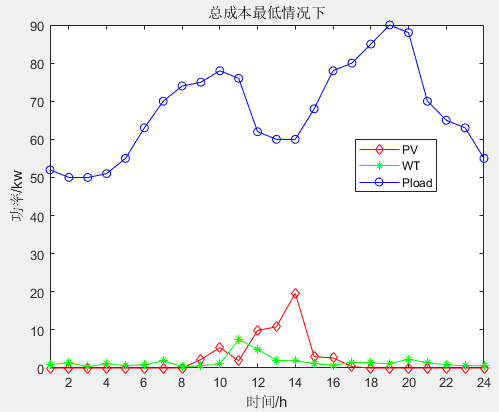
单目标应用:基于蜘蛛蜂优化算法(Spider wasp optimizer,SWO)的微电网优化调度MATLAB
一、微网系统运行优化模型 微电网优化模型介绍: 微电网多目标优化调度模型简介_IT猿手的博客-CSDN博客 二、蜘蛛蜂优化算法 蜘蛛蜂优化算法(Spider wasp optimizer,SWO)由Mohamed Abdel-Basset等人于2023年提出,该…...
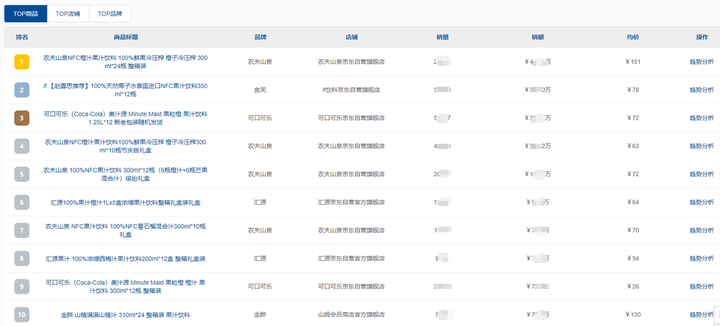
2023年7月京东饮料行业数据分析(京东运营数据分析)
饮料消费已成为当下快消品行业里的主力军,随着社会群体喜好的改变、消费群体的不断扩大,可选择的饮料种类越来越多,我国饮料市场的体量也较为庞大。根据鲸参谋电商数据分析平台的数据显示,今年7月份,京东平台饮料的销量…...

执行 JUnit 单元测试前,修改环境变量
同一份代码,在不改变配置文件的情况下,可以连接不同的数据库,进行JUnit测试。 非开发、测试、生产环境的区别。而是 我就站在这里,指哪打哪! 避免重复造轮子,参考博文: 使用junit&spri…...

openGauss学习笔记-63 openGauss 数据库管理-资源池化架构
文章目录 openGauss学习笔记-63 openGauss 数据库管理-资源池化架构 openGauss学习笔记-63 openGauss 数据库管理-资源池化架构 本文档主要介绍资源池化架构下的一些最佳实践和使用注意事项,用于支撑对相关特性感兴趣的开发者可以快速部署、实践或进行定制化开发。…...
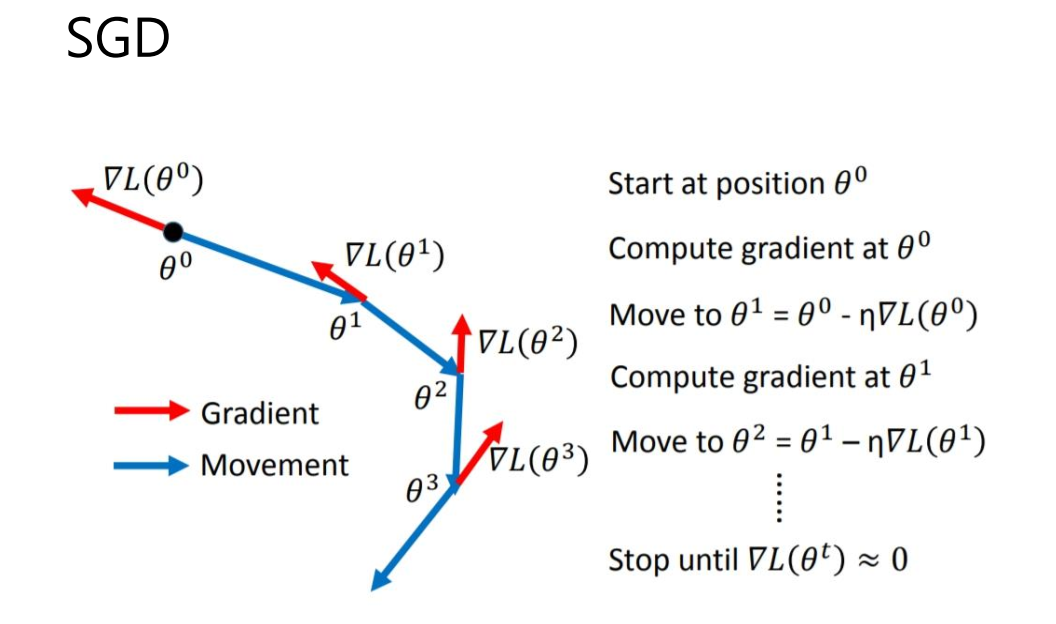
计算机竞赛 基于深度学习的植物识别算法 - cnn opencv python
文章目录 0 前言1 课题背景2 具体实现3 数据收集和处理3 MobileNetV2网络4 损失函数softmax 交叉熵4.1 softmax函数4.2 交叉熵损失函数 5 优化器SGD6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 **基于深度学习的植物识别算法 ** …...

ChatGPT如何应对紧急情况和灾害应对?
ChatGPT是一个文本生成模型,它可以用于各种任务,但在处理紧急情况和灾害应对方面,它有一些潜在的用途和限制。在这篇文章中,我们将讨论ChatGPT在紧急情况和灾害应对中的应用,以及如何充分利用这一技术,并提…...

ElementUI浅尝辄止37:Select 选择器
当选项过多时,使用下拉菜单展示并选择内容。 1.如何使用?基础单选 v-model的值为当前被选中的el-option的 value 属性值 <template><el-select v-model"value" placeholder"请选择"><el-optionv-for"item in …...

PCL 基于任意四点计算球心坐标
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 继续基于之前的思路PCL 基于三个点计算圆心坐标之二(二维),假设存在四个不共面的点, ( x 1 , y 1 ) (x_1,y_1)...
飞书即时消息无需API开发连接Cohere,打造飞书AI智能问答助手
飞书即时消息用户使用场景: 许多企业都在使用飞书系统进行协同办公,而现在有了Cohere大语言模型技术,能够根据用户的提问来自动产生回答,无需人为干预。对于企业负责人来说,他们认为如果将Cohere技术融入到飞书机器人中…...

FPGA实现Cordic算法——向量模式
FPGA实现Cordic算法——向量模式 FPGA实现Cordic算法——向量模式1.cordic算法基本原理2.FPGA实现cordic算法向量模式i、FPGA串行实现cordicii、FPGA流水线实现cordiciii、实验结果 FPGA实现Cordic算法——向量模式 1.cordic算法基本原理 FPGA中运算三角函数,浮点数…...
【常用代码14】el-input输入框内判断正则,只能输入数字,过滤汉字+字母。
问题描述: el-input输入框,只能输入数字,但是不能显示输入框最右边的上下箭头, <el-input v-model"input" type"number" placeholder"请输入内容" style"width: 200px;margin: 50px 0;&…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
