# 将PCL点云转换为Eigen向量进行运算
将PCL点云转换为Eigen向量进行运算
在处理点云数据时,我们常需要将PCL中的点云转换为Eigen向量,进行一些矩阵运算。这里介绍PCL点云到Eigen向量的两种转换方法。
点云转换为Eigen数组
对于一个PCL的点云,可以通过getArray4fMap()函数获取Eigen数组表示:
// PCL点云
pcl::PointCloud<pcl::PointXYZ>::Ptr cloudPtr (new pcl::PointCloud<pcl::PointXYZ>);// 转换为Eigen数组
Eigen::Array4f cloud = cloudPtr->getArray4fMap();// 转换为向量进行运算
Eigen::Vector4f pt = cloud.row(i);
这样就可以获得整个点云的数据的Eigen数组表示,然后提取出需要的点进行向量运算。
单点转换为Eigen向量
对于pcl::PointXYZ类型的单个点,有以下几种转换方式:
pcl::PointXYZ pt;// 方法1:通过坐标访问
Eigen::Vector3f eigen_pt(pt.x, pt.y, pt.z); // 方法2:直接赋值转换
Eigen::Vector3f eigen_pt = pt.getVector3fMap();// 方法3:通过Array转换
Eigen::Array3f array(pt.data);
Eigen::Vector3f eigen_pt = array;
主要是通过获取坐标映射或数组来获得Eigen向量表示。
这样我们就可以方便地在PCL和Eigen之间转换点云数据,利用Eigen进行一些矩阵运算和处理。
——本文由AI生成
相关文章:

# 将PCL点云转换为Eigen向量进行运算
将PCL点云转换为Eigen向量进行运算 在处理点云数据时,我们常需要将PCL中的点云转换为Eigen向量,进行一些矩阵运算。这里介绍PCL点云到Eigen向量的两种转换方法。 点云转换为Eigen数组 对于一个PCL的点云,可以通过getArray4fMap()函数获取Eigen数组表示: // PCL点云 pcl::Po…...
elmentui表单重置及出现的问题
一、表单: 二、代码——拿官方的代码举例(做了一些小改动): 改动:model绑定的字段,由form改为queryParams ref绑定的字段form改为queryFrom 注:model绑定的这个字段用来做数据双向绑定的 注:ref绑定的这…...

游戏平台加盟该怎么做?需要准备什么?
游戏平台加盟是一种合作模式,允许个人或企业以加盟商的身份参与游戏平台,并从中获得一定的权益和收益。以下是一些步骤和需要准备的事项,来考虑如何进行游戏平台加盟: 步骤: 研究市场和平台:了解游戏市场和…...

selenium中定位shadow-root,以及获取shadow-root内部的数据
通过shadow-root的父级定位到shadow-root,再通过语句进行操作 两种方法: 第一种,Python种JS实现 第二种,selenium实现 1.0 案例网站 参考某橘色网站 2.0 js语句定位 可在控制台进行测试 测试语句 document.querySelector("ali-ba…...

OpenCV(三十二):轮廓检测
1.轮廓概念介绍 在计算机视觉和图像处理领域中,轮廓是指在图像中表示对象边界的连续曲线。它是由一系列相邻的点构成的,这些点在边界上连接起来形成一个封闭的路径。 轮廓层级: 轮廓层级(Contour Hierarchy)是指在包含…...

接口自动化测试做线上巡检,如何避免数据污染
在接口自动化测试中,避免数据污染是非常重要的,特别是在线上环境中进行巡检。 1. 使用独立的测试环境:建议使用专门的测试环境来进行接口自动化测试,而不是直接在生产环境中进行。测试环境应该是一个独立的、与生产环境隔离的环境…...

C++ 指针
C 指针 学习 C 的指针既简单又有趣。通过指针,可以简化一些 C 编程任务的执行,还有一些任务,如动态内存分配,没有指针是无法执行的。所以,想要成为一名优秀的 C 程序员,学习指针是很有必要的。 正如您所知…...

SpringBoot集成kubernetes-client升级k8s后初始化失败问题
SpringBoot集成kubernetes-client升级k8s后初始化失败问题 1.问题描述 程序以前使用的k8s版本是1.16,fabric8.kubernetes-client的版本是4.10.2,springboot版本是2.3.5。由于环境切换,这次需要升级k8s的版本,现在将k8s版本升级到…...
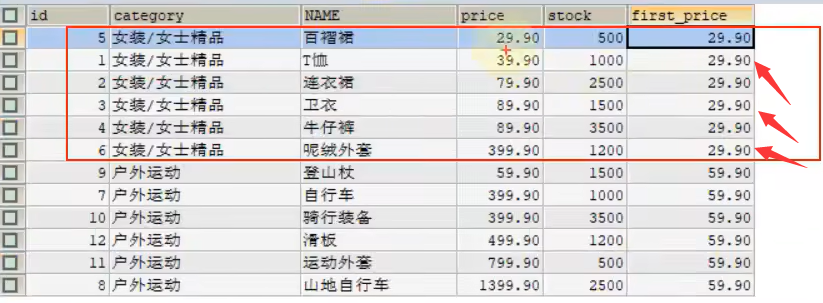
MySQL 学习笔记
😀😀😀创作不易,各位看官点赞收藏. 文章目录 MySQL 学习笔记1、DQL 查询语句1.1、基本查询1.2、函数查询1.2.1、单行函数1.2.2、聚合函数 1.3、复杂查询1.3.1、连接查询1.3.2、子查询 1.4、SQL 语句 执行顺序 2、DDL 定义语句2.1、…...

Docker 的常用命令
0 基本命令 概述 [root192 home]# docker --helpUsage: docker [OPTIONS] COMMANDA self-sufficient runtime for containersOptions:--config string Location of client configfiles (default "/root/.docker")-c, --context string Name of the context…...

嵌入式-电子电路四个基本定律
目录 1、欧姆定律 2、焦耳定律 3、基尔霍夫电流定律 4、基尔霍夫电压定律 1、欧姆定律 欧姆定律是关于导体两端电压与导体中电流关系的定律。具体表述为:在同一电路中,通过某段导体的电流跟这段导体两端的电压成正比,跟这段导体的电阻成反…...

【linux命令讲解大全】083.Linux 常用命令ispell , spell , atrm, chattr
文章目录 ispell补充说明语法参数 spell补充说明语法参数 atrm补充说明语法选项参数 实例 chattr补充说明语法选项 实例 从零学 python ispell 检查文件中出现的拼写错误。 补充说明 ispell命令用于检查文件中出现的拼写错误。 语法 ispell [参数] 参数 文件:…...

JAVA实现SAP接口
JAVA实现SAP接口 环境spring-bootmaven 1.maven依赖 <dependency><groupId>com.github.virtualcry</groupId><artifactId>sapjco-spring-boot-starter</artifactId><version>3.1.4</version></dependency>2.配置文件 applic…...

华南理工大学811信号与系统考研分数线,招生人数,报考统计,考情分析,就业,真题,大纲,参考书,华工811
华南理工大学811信号与系统考研分数线,招生人数,报考统计,考情分析,就业,真题,大纲,参考书,华工811 华南理工大学811信号与系统考研分数线,招生人数,报考统…...

Android 字符串 占位符
在 Android 中,字符串中的 % 后面跟着的字符称为格式化占位符,用于指示在运行时将值插入到字符串中的位置,并指定插入的值的类型。常见的格式化占位符类型如下: %s:字符串占位符。它用于插入字符串值。 String name …...

vue页面添加水印(可用于H5,APP)
vue页面添加水印 背景实现新建vue组件使用效果 尾巴 背景 最近实现了一个小功能,就是给页面添加背景水印。实现思路就是定义一个宽高充满屏幕的组件,然后使用绝对定位并通过层级控制让水印显示在页面的最前端。 实现 代码相对简单,相信有点…...
下载git
1.官网下载可能会有访问失败 2.用其他的镜像源下载 快 准 狠 CNPM Binaries Mirror...

MSYS2 如何切换镜像源(附带脚本自动修改)
这篇文章将总结【如何切换MSYS2镜像】,其实比较简单,但还是记录一下吧。 下面示例中附带一个脚本,这样你就不用一个个手动修改了。 1. 镜像服务配置文件 MSYS2 的所有镜像服务配置,都在其安装路径下的etc/pacman.d目录下 可以看到…...

使用ICMP协议来判断UDP端口的存活状态
我们使用了原始套接字(socket.SOCK_RAW)来发送和接收ICMP消息,也就是通过模拟ICMP协议来进行UDP端口的探测。我们构造了一个简单的ICMP数据包,并将其发送到目标主机的特定端口。然后,我们等待接收目标主机返回的ICMP消…...

VUE for循环 默认选中第一条数据
for循环渲染列表默认选中第一条数据 点击其他选项切换数据 <div><div class"Subtitle" style"padding: 5px 40px;">项目清单</div><div class"project-manifest"><div v-for"(item, index) in project" :…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
