图的应用(最小生成树,最短路径,有向无环图)
目录
一.最小生成树
1.生成树
2.无向图的生成树
3.最小生成树算法
二.最短路径
1.单源最短路径---Dijkstra(迪杰斯特拉)算法
2.所有顶点间的最短路径---Floyd(弗洛伊德)算法
三.有向无环图的应用
1.AOV网(拓扑排序)
2.AOE网(关键路径)
一.最小生成树
1.生成树
所有顶点均有边连接在一起,但不存在回路的图

•一个图可以有许多棵不同的生成树
•所有生成树都具有以下共同特点
•生成树的顶点个数与图的顶点个数相同
•生成树是图的极小连通子图,去掉一条边则非连通
•一个有n个顶点的连通图的生成树有(n-1)条边
•在生成树中再加一条边必然形成回路
•生成树中任意两个顶点间的路径是唯一的
•含n个顶点n-1条边的图不一定是生成树
2.无向图的生成树
无向图的生成树可以与深度优先搜索遍历与广度优先搜索遍历的方法结合起来
不了解的可以看看这篇
深度优先搜索遍历与广度优先搜索遍历
深度优先生成树:V1->V2->V4->V8->V5->V3->V6->V7
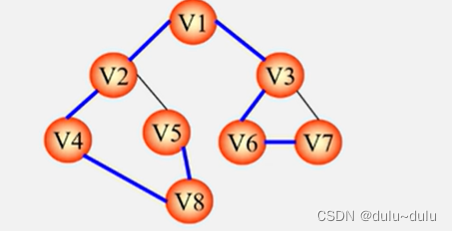
广度优先生成树:V1->V2->V3->V4->V5->V6->V7->V8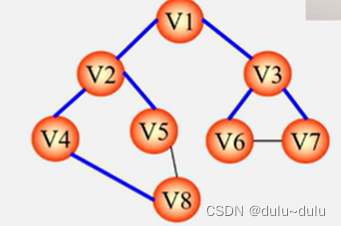
3.最小生成树算法
给定一个无向网络,在该网所有的生成树中,使得各边权值之和最小的那棵生成树称为最小生成树,也叫最小代价生成树
生成最小生成树的方法
MST(Minimum Spanning Tree)
•已落在生成树上的顶点集:U
•尚未落在生成树的顶点集:V-U
•选取权值最小的边,因为权值最小的边一定存在生成树是包含他的
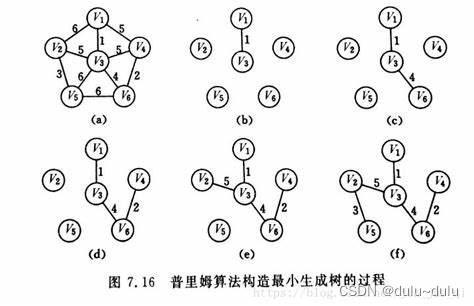
(1)普里姆(Prim)算法
•设N=(V,E)是连通网,TE是N上最小生成树中边的集合
•初始令 U={u0},(u0V), TE={}
•在所有 uU, v
V-U的边(u v)
E中,找条代价最小的边(u0,v0)
•将(u0,v0)并入集合 TE,同时v0并入 U
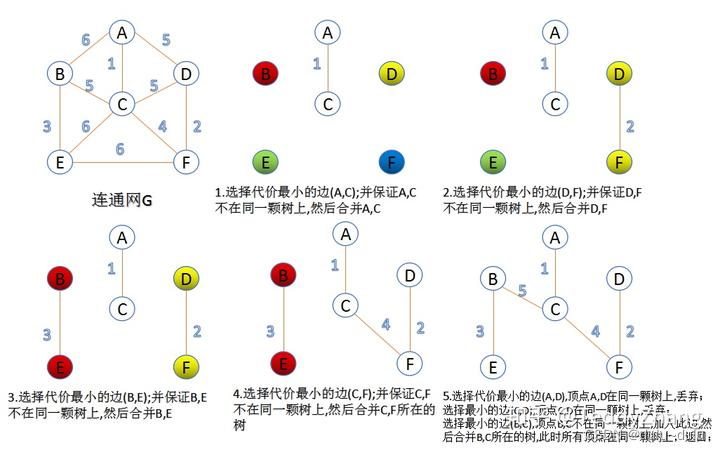
(2)克鲁斯卡尔(Kruskal)算法
•设连通网 N=(V,E),令最小生成树初始状态为只有 n个顶点而无边的非连通图T=(V,{}),每个顶点自成一个连通分量。
•在E中选取代价最小的边,若该边依附的顶点落在T中不同的连通分量上(即:不能形成环),则将此边加入到 T中;否则,舍去此边,选取下一条代价最小的边。
•依此类推,直至T中所有顶点都在同一连通分量上为止。
(3)两种算法的区别
•普里姆算法是选择点,从U集合到V-U集合找一条权值最小的边,将这个边连接的点加入到U集合中,而克鲁斯卡尔算法则是在所有边中找权值最小的边,加入到生成树中,直到所有的点连通,边为n-1条。
•普里姆算法的时间复杂度为O(),对于所有的点,都需要遍历其他顶点进行判断下一个加入生成树的点,克鲁斯卡尔算法则是选择边,和顶点数无关,只跟边数有关,对顶点的权值进行排序时,平均情况是(eloge)
•克鲁斯卡尔算法时间复杂度只跟边数有关,所以边数较少时,算法时间较少,所以克鲁斯卡尔算法适用于稀疏图,普里姆算法适用于稠密图。

二.最短路径
在有向网中A点(源点)到达B点(终点)的多条路径中,寻找一条各边权值之和最小的路径,即最短路径
最短路径与最小生成树不同,路径上不一定包含n个顶点,也不一定包含n-1条边
•两点间的最短路径
下图最短路径值为14
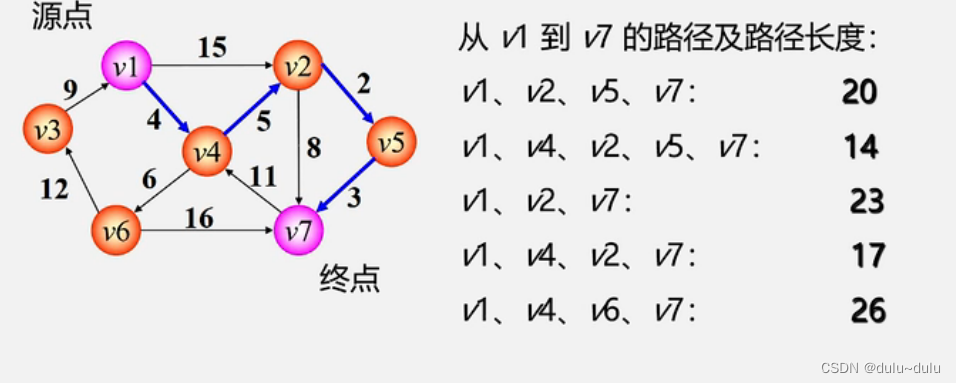
•某源点到其他各点最短路径
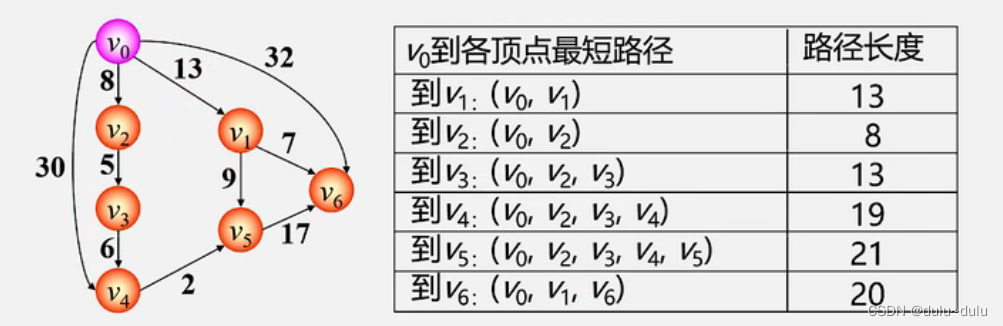
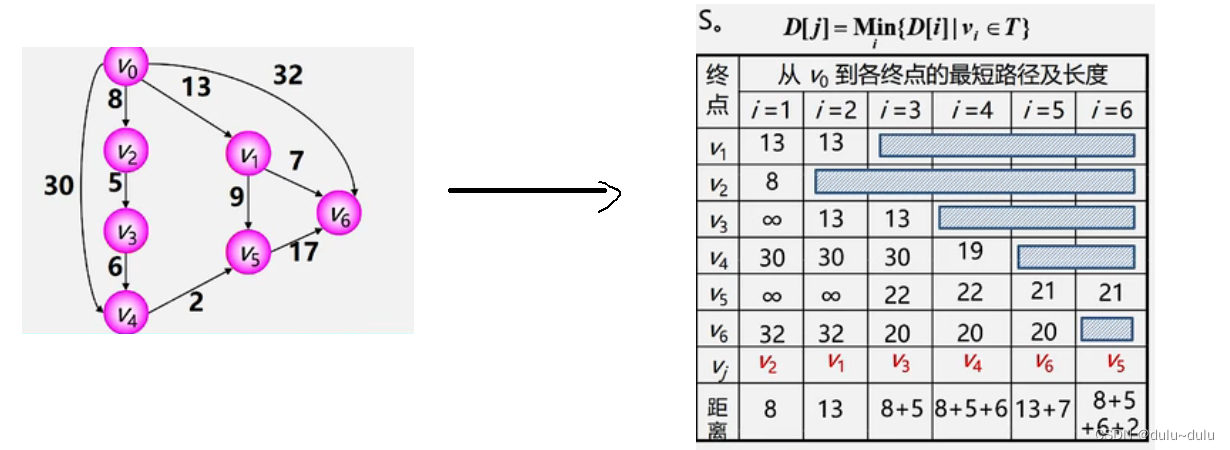
1.单源最短路径---Dijkstra(迪杰斯特拉)算法
算法步骤
•初始时令S={v0},T={其余顶点}
•T中顶点对应的距离值用辅助数组D存放
•D[i]初值:若<v0,>存在,则为权值;否则为
•从T中选取一个其距离值最小的顶点,加入S
•对T中顶点的距离值进行修改:若加进作中间顶点,从v0到
的距离值比不加
的路径要短,则修改此距离值。
•重复上述步骤,直到S=V为止
以下图为例
Dijkstra(迪杰斯特拉)算法可以计算1个顶点到其他顶点的最短路径,时间复杂度为O(
)
如果要计算所有顶点间的最短路径,即O(
)*n=O(
)
2.所有顶点间的最短路径---Floyd(弗洛伊德)算法
算法步骤
•逐个顶点试探
•从vi到vj的所有可能存在的路径中
•选出一条长度最短的路径
初始设置一个n阶方阵,令其对角线元素为0,若存在弧<vi,vj>,则对应元素为权值;否则为
如图:A-->B的权值为4,B-->A的权值为6,以此类推,可得n阶方阵
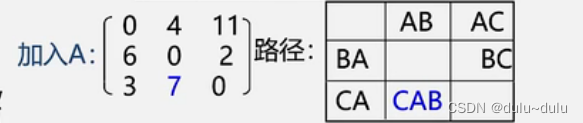
加入A顶点,如图,本来C--->B没有路径(
),但是可以从C-->A--->B,路径长度为7
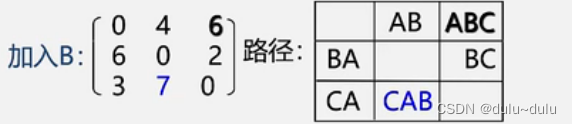
加入B,如图,原来A--->C为11,现在加入B,变为A--->B--->C,变得更小了,所以6替换11
加入C,如图,B--->A路径长度为6,B--->C--->A路径长度变短,所以5替换6
以上总结为:逐步试着在原直接路径中增加中间顶点,若加入中间顶点后路径变短,则修改之;否则,维持原值。所有顶点试探完毕,算法结束。
三.有向无环图的应用
1.AOV网(拓扑排序)
用一个有向图表示一个工程的各子工程及其相互制约的关系,其中以顶点表示活动,弧表示活动之间的优先制约关系,称这种有向图为顶点表示活动的网,简称 AOV网(Activity On Vertex network)
拓扑排序
拓扑排序的方法
•在有向图中选一个没有前驱的顶点且输出之
•从图中删除该顶点和所有以它为尾的弧
•重复上述两步,直至全部顶点均已输出或者当图中不存在无前驱的顶点为止
注:拓扑排序的结果是不唯一的
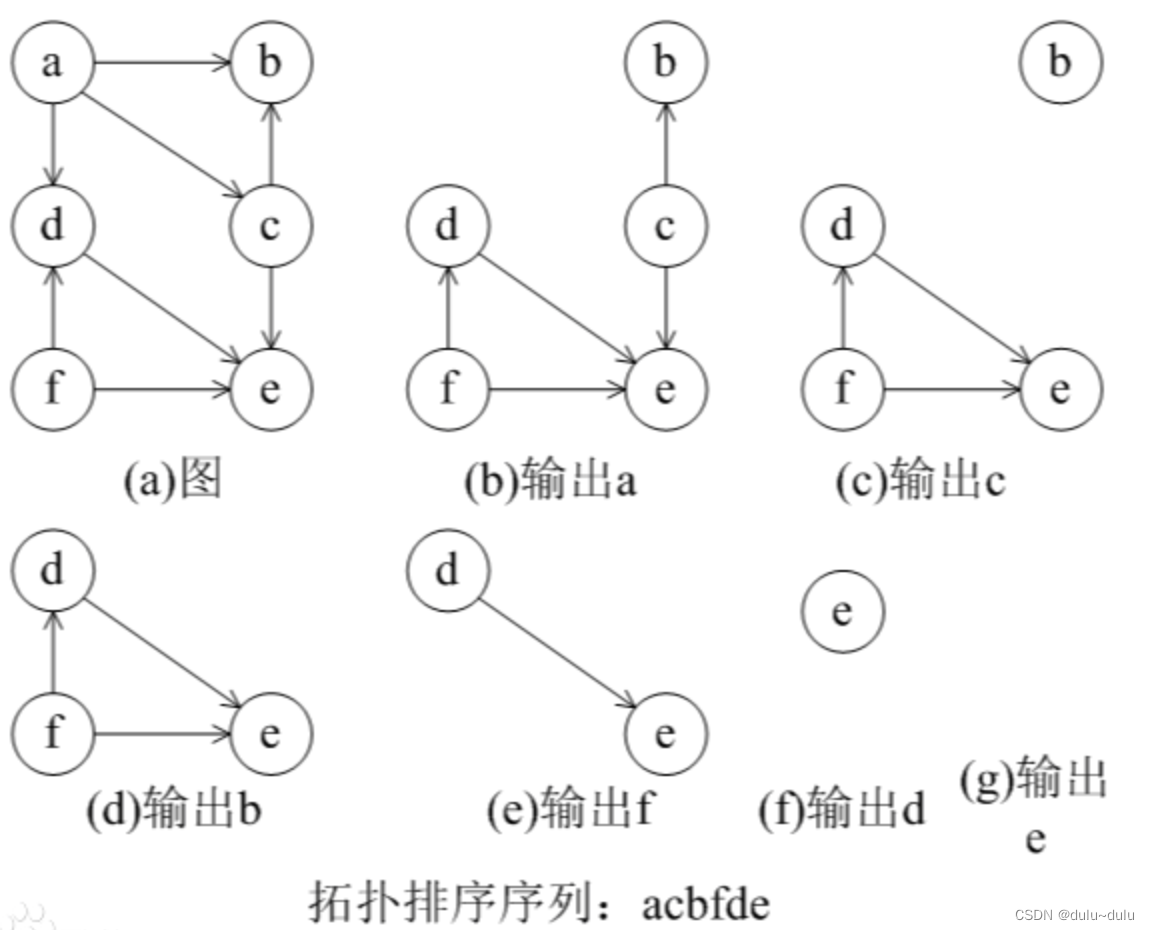
拓扑排序可以检测AOV网中是否存在环
对有向图构造其顶点的拓扑有序序列,若网中所有顶点都在它的拓扑有序序列中,则该AOV 网必定不存在环,若还剩余顶点没有在拓扑有序序列中,就存在环
2.AOE网(关键路径)
用一个有向图表示一个工程的各子工程及其相互制约的关系,以弧表示活动,以顶点表示活动的开始或结束事件,称这种有向图为边表示活动的网,简称为AOE网(Activity On Edge)。
关键路径
关于关键路径,可以看这篇文章
http://t.csdn.cn/uitVf
如果想要理解的再深入一些,可以看
http://t.csdn.cn/JfbLs
相关文章:

图的应用(最小生成树,最短路径,有向无环图)
目录 一.最小生成树 1.生成树 2.无向图的生成树 3.最小生成树算法 二.最短路径 1.单源最短路径---Dijkstra(迪杰斯特拉)算法 2.所有顶点间的最短路径---Floyd(弗洛伊德)算法 三.有向无环图的应用 1.AOV网(拓扑…...

python正则表达式笔记2
由 \ 和一个字符组成的特殊序列在以下列出。 如果普通字符不是ASCII数位或者ASCII字母,那么正则样式将匹配第二个字符。比如,\$ 匹配字符 $. \number 匹配数字代表的组合。每个括号是一个组合,组合从1开始编号。 比如 (.) \1 匹配 the the 或…...

matplotlib 的默认字体和默认字体系列
matplotlib 的默认字体和默认字体系列 查看默认字体和默认字体系列查看默认字体系列下包含的字体查看 plt.rcParams 设置的所有参数查看所有支持的字体格式设置默认字体方法1:方法2 今天给大家介绍一下 matplotlib 包中的默认字体以及默认字体系列。 查看默认字体和…...
STMCUBEMX_IIC_DMA_AT24C64读取和写入
STMCUBEMX_IIC_DMA_AT24C64读取和写入 说明: 1、此例程只是从硬件IIC升级到DMA读写,因为暂时存储的掉电不丢失数据不多,一页就可以够用,不用担心跨页读写的问题 2、使用DMA后,程序确实是变快了,但是也要注意…...

wsl2相关问题
磁盘空间 wsl 删除相关文件后,如删除docker 无用的容器和镜像,windows上磁盘仍然无法自动回收空间 (参考:[microsoft/WSL](https://github.com/microsoft/WSL/issues/4699#issuecomment-627133168)) # 如清除无用do…...

使用idea时,光标变成了不能按空格键,只能修改的vim格式,怎么切换回正常光标
情况1 你可能不小心启用了 IntelliJ IDEA 中的 Vim 插件。你可以尝试以下步骤来禁用它: 在 IntelliJ IDEA 中,选择 "File" -> "Settings" (如果你在 macOS 上,选择 "IntelliJ IDEA" -> &quo…...
vue+antd——实现table表格的打印——分页换行,每页都有表头——基础积累
这里写目录标题 场景效果图功能实现1:html代码功能实现2:css样式功能实现3:js代码补充内容page-break-inside 属性page-break-after属性page-break-before 属性 场景 最近在写后台管理系统时,遇到一个需求,就是要实现…...

linux C MD5计算
#include <stdio.h> #include <string.h> #include <openssl/md5.h>int main() {char str[] "Hello, world!"; // 需要计算MD5哈希值的字符串unsigned char digest[MD5_DIGEST_LENGTH]; // 存储MD5哈希值的数组MD5((unsigned char*)&str, str…...
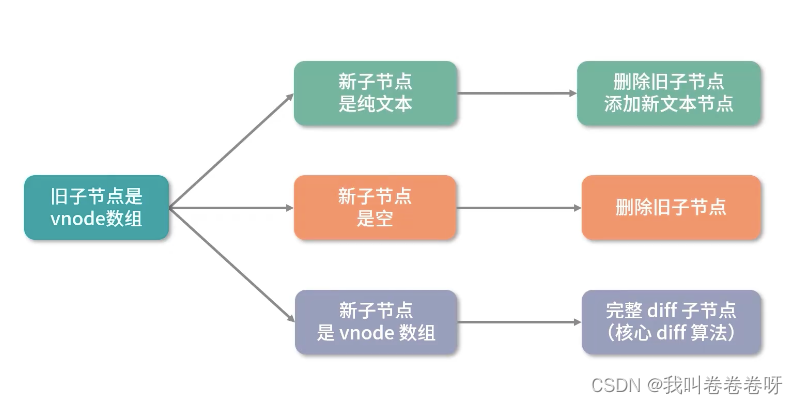
vue3学习源码笔记(小白入门系列)------ 组件更新流程
目录 说明例子processComponentcomponentUpdateFnupdateComponentupdateComponentPreRender 总结 说明 由于响应式相关内容太多,决定先接着上文组件挂载后,继续分析组件后续更新流程,先不分析组件是如何分析的。 例子 将这个 用例 使用 vi…...

数学建模B多波束测线问题B
数学建模多波束测线问题 1.问题重述: 单波束测深是一种利用声波在水中传播的技术来测量水深的方法。它通过测量从船上发送声波到声波返回所用的时间来计算水深。然而,由于它是在单一点上连续测量的,因此数据在航迹上非常密集,但…...

Pytest 框架执行用例流程浅谈
背景: 根据以下简单的代码示例,我们将从源码的角度分析其中的关键加载执行步骤,对pytest整体流程架构有个初步学习。 代码示例: import pytest def test_add(): assert 1 1 2 def test_sub(): assert 2 - 1 1 通过 pytes…...

C#__资源访问冲突和死锁问题
/// 线程的资源访问冲突:多个线程同时申请一个资源,造成读写错乱。 /// 解决方案:上锁,lock{执行的程序段}:同一时刻,只允许一个线程访问该程序段。 /// 死锁问题: /// 程序中的锁过多…...

机器学习——Logistic Regression
0、前言: Logistic回归是解决分类问题的一种重要的机器学习算法模型 1、基本原理: Logistic Regression 首先是针对二分类任务提出的一种分类方法如果将概率看成一个数值属性,则二元分类问题的概率预测就可以转化为一个回归问题。这种思路最…...

创建husky规范前端项目
创建husky规范前端项目 .husky文件是一个配置文件,用于配置Git钩子。Git钩子是在Git操作时触发的脚本,可以用于自动化一些任务,比如代码格式化、代码检查、测试等。.husky文件可以指定在Git的不同操作(如commit、push等ÿ…...

深浅拷贝与赋值
数据类型 数据类型 在JavaScript中,数据类型有两大类。一类是基本数据类型,一类是引用数据类型。 基本数据类型有六种:number、string、boolean、null、undefined、symbol。 基本数据类型存放在栈中。存放在栈中的数据具有数据大小确定&a…...

bert ranking pairwise demo
下面是用bert 训练pairwise rank 的 demo import torch from torch.utils.data import DataLoader, Dataset from transformers import BertModel, BertTokenizer from sklearn.metrics import pairwise_distances_argmin_minclass PairwiseRankingDataset(Dataset):def __ini…...
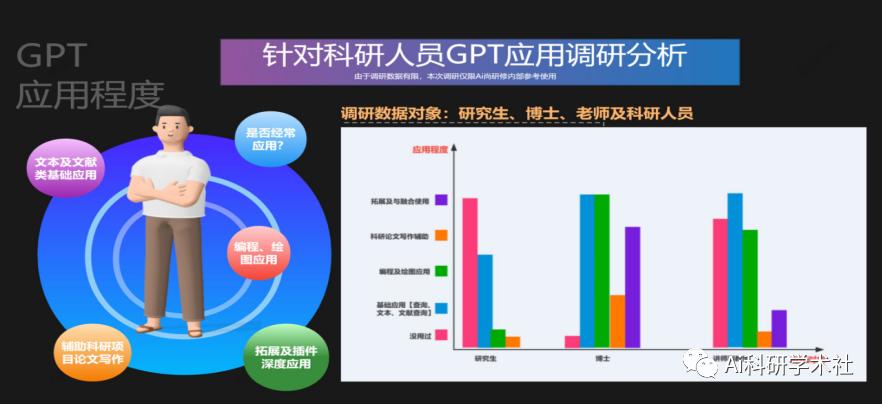
GPT引领前沿与应用突破之GPT4科研实践技术与AI绘图
GPT对于每个科研人员已经成为不可或缺的辅助工具,不同的研究领域和项目具有不同的需求。例如在科研编程、绘图领域:1、编程建议和示例代码: 无论你使用的编程语言是Python、R、MATLAB还是其他语言,都可以为你提供相关的代码示例。2、数据可视…...
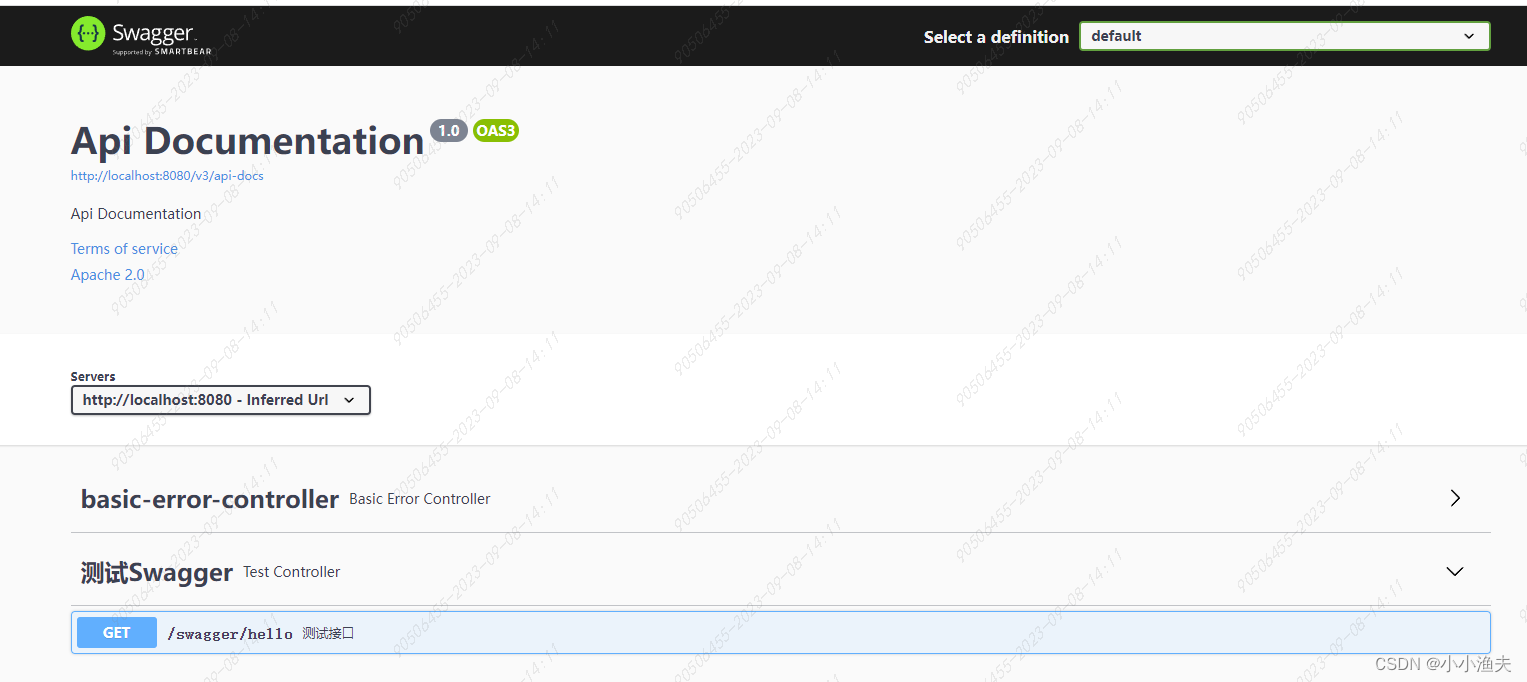
SpringBoot整合Swagger3
前言 swagger是啥,是干什么的,有什么用,我想在这里我就不用介绍了,下面直接代码演示。 添加依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0…...

detectron2 install path
>>> import detectron2 >>> detectron2_path detectron2.__file__ >>> print(detectron2.__file__)...
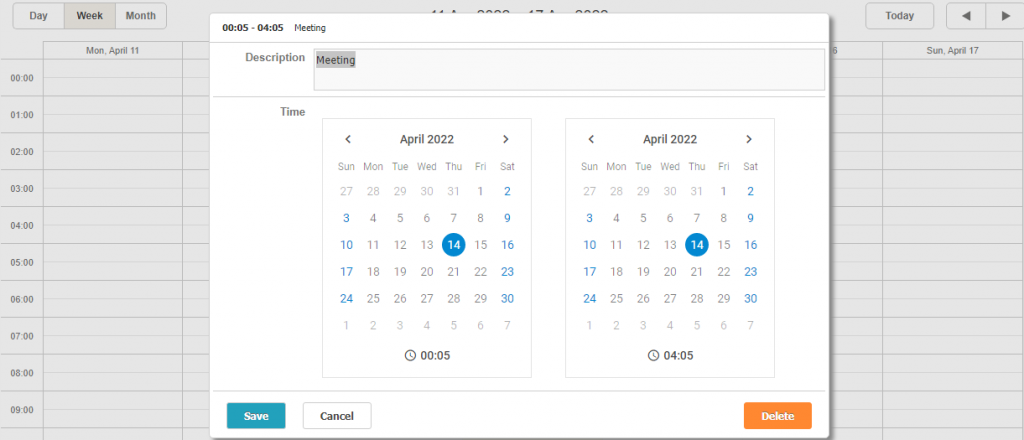
如何将DHTMLX Suite集成到Scheduler Lightbox中?让项目管理更可控!
在构建JavaScript调度器时,通常需要为最终用户提供一个他们喜欢的方式来计划事件,这是Web开发人员喜欢认可DHTMLX Scheduler的重要原因,它在这方面提供了完全的操作自由,它带有lightbox弹出窗口,允许通过各种控件动态更…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...