2021 ICPC 昆明 I Mr Main and Windmills(直线与线段的交点)
2021 ICPC 昆明 I Mr. Main and Windmills(直线与线段的交点)
I Mr. Main and Windmills
大意:给出一条线段 , 一个人从线段的起点走到线段的终点 , 线段的一侧有若干风车 , 当前的人在线段上的每一个位置观察风车都会得到一个顺序 。多次询问第 i 号风车被观察的位置第k次改变时人在线段上的位置。
思路:不难发现 , 两个风车交换位置当且仅当人走过 两风车所在直线与线段交点的时候 , 两两枚举风车求直线与线段交点 , 然后根据和起始点的距离排序后根据要求输出即可。
易错点:这里线段与直线求交会有一个易错点。
如果先求 线段所在直线与风车直线的交点(line_make_point) , 然后再判断交点是否在线段上(point_on_segment) , 这样误差会巨大。因为直线求交会有除法 , 求出的交点存在误差 ,然后判断点在线段上时会用到叉积 , 叉积的几何意义就是形成三角形的面积 , 如果线段特别特别长 , 叉积就会很大 , 从而在这里产生错误。
if(!line_make_point(l , r , now)) continue;
if(!point_on_segment(now , st , ed)) continue;
解决方法:
1. 对于求交问题 , 先判断在求交
对应在这里 , 就可以先判断线段和直线是否相交(toleft) , 相交求交点即可 , 这样是不会有判断误差的产生的。
if(toleft(st , p[i] , p[j]) * toleft(ed , p[i] , p[j]) > 0) continue;
line_make_point(l , r , now);
2. double 换成 long double , 容限(eps) 调大即可
这里推荐第一种 , 第一种更规范
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 1e3 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;//--------------------------------------------------------------
const double eps = 1e-9;
const double pi = acos(-1);
inline double sqr(double x) {return x * x;} //平方
int sign(double x){if(fabs(x) < eps) return 0;if(x > 0) return 1;return -1;
}//符号
struct point{double x , y;point(){}point(double a , double b) : x(a) , y(b){}friend point operator + (const point &a , const point &b){return point(a.x + b.x , a.y + b.y);}friend point operator - (const point &a , const point &b){return point(a.x - b.x , a.y - b.y);}friend bool operator == (const point &a , const point &b){return !sign(a.x - b.x) && !sign(a.y - b.y);}friend point operator * (const point &a , const double &b){return point(a.x * b , a.y * b);}friend point operator * (const double &a , const point &b){return point(a * b.x , a * b.y);}friend point operator / (const point &a , const double &b){return point(a.x / b , a.y / b);}//向量模长 double norm(){ return sqrt(sqr(x) + sqr(y));}
}; struct line{point a , b;line(){}line(point x , point y) : a(x) , b(y) {}
};double det(const point &a , const point &b){return a.x * b.y - a.y * b.x;
}//叉积 判断两点共线 double dot(const point &a , const point &b){return a.x * b.x + a.y * b.y;
}//点积double dist(const point &a , const point &b){return (a - b).norm();
}//两点距离point rotate_point(const point &a , const point &p , double A){double tx = p.x - a.x , ty = p.y - a.y;return point(a.x + tx * cos(A) - ty * sin(A) , a.y + tx * sin(A) + ty * cos(A));
}// p 点 绕 a 点逆时针旋转 A 弧度int toleft(const point &p , const point &a , const point &b) {return sign(det(b - a , p - a));// 1 左 0 上 -1 右
}//只适用凸多边形//判断点 p 是否在线段 st 上(包括端点)
bool point_on_segment(point p , point s , point t){return sign(det(p - s , t - s)) == 0 && sign(dot(p - s , p - t)) <= 0;
}bool parallel(line a , line b){return !sign(det(a.a - a.b , b.a - b.b));
}bool line_make_point(line a , line b , point &res){if(parallel(a , b)) return 0;double s1 = det(a.a - b.a , b.b - b.a);double s2 = det(a.b - b.a , b.b - b.a);res = (s1 * a.b - s2 * a.a) / (s1 - s2);return 1;
}
//--------------------------------------------------------------
//--------------------------------------------------------------int n , m;
point st , ed , p[N] , now;
double x , y;
int h , k;vector<tuple<double , double , double>>ans[N];signed main(){IOScout << fixed << setprecision(10);cin >> n >> m;cin >> x >> y;st = point{x , y};cin >> x >> y;ed = point{x , y};for(int i = 1 ; i <= n ; i ++){cin >> x >> y;p[i] = point{x , y};}line l = line{st , ed};for(int i = 1 ; i <= n ; i ++){for(int j = i + 1 ; j <= n ; j ++){line r = line{p[i] , p[j]};if(toleft(st , p[i] , p[j]) * toleft(ed , p[i] , p[j]) > 0) continue;line_make_point(l , r , now);ans[i].emplace_back(now.x , now.y , dist(now , st));ans[j].emplace_back(now.x , now.y , dist(now , st));} }for(int i = 1 ; i <= n ; i ++) sort(ans[i].begin() , ans[i].end() , [&](tuple<double , double , double> a , tuple<double , double , double> b){return get<2>(a) < get<2>(b);});for(int i = 1 ; i <= m ; i ++){cin >> h >> k;if(ans[h].size() < k){cout << "-1\n";}else{auto [x , y , z] = ans[h][k - 1];cout << x << " " << y << "\n";}}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
相关文章:
)
2021 ICPC 昆明 I Mr Main and Windmills(直线与线段的交点)
2021 ICPC 昆明 I Mr. Main and Windmills(直线与线段的交点) I Mr. Main and Windmills 大意:给出一条线段 , 一个人从线段的起点走到线段的终点 , 线段的一侧有若干风车 , 当前的人在线段上的每一个位置观察风车都会得到一个顺…...
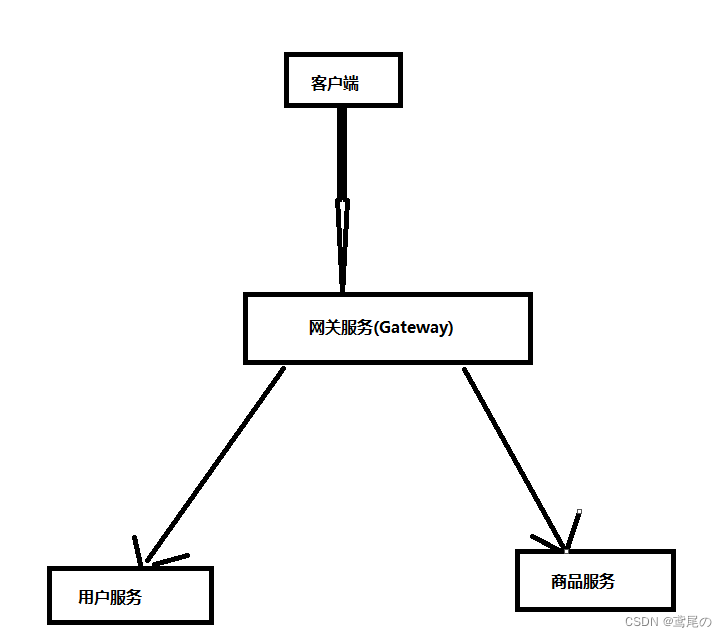
SpringCloudAlibaba Gateway(一)简单集成
SpringCloudAlibaba Gateway(一)简单集成 随着服务模块的增加,一定会产生多个接口地址,那么客户端调用多个接口只能使用多个地址,维护多个地址是很不方便的,这个时候就需要统一服务地址。同时也可以进行统一认证鉴权的需求。那么服…...

逻辑回归(Logistic Regression)
1.分类问题 在分类问题中,你要预测的变量 y是离散的值,我们将学习一种叫做逻辑回归 (Logistic Regression) 的算法,这是目前最流行使用最广泛的一种学习算法。 在分类问题中,我们尝试预测的是结果是否属于某一个类(例…...
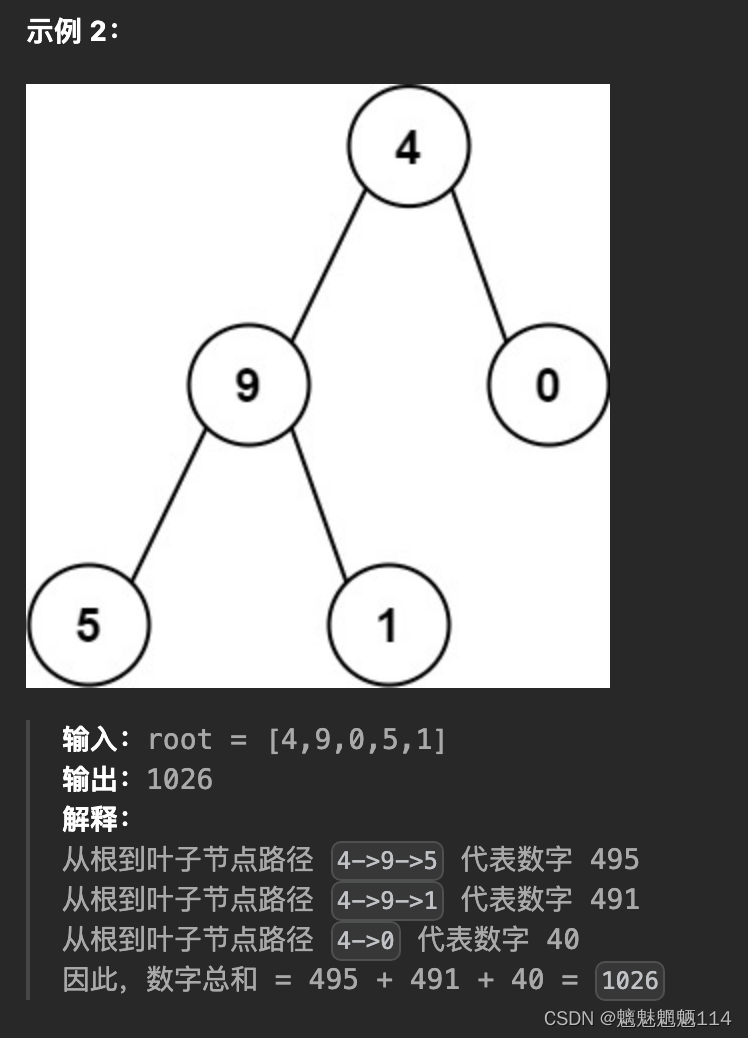
Leetcode129. 求根到叶子节点数字之和
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表一个数字: 例如,从根节点到叶子节点的路径 1 ->…...

0401hive入门-hadoop-大数据学习.md
文章目录 1 Hive概述2 Hive部署2.1 规划2.2 安装软件 3 Hive体验4 Hive客户端4.1 HiveServer2 服务4.2 DataGrip 5 问题集5.1 Could not open client transport with JDBC Uri 结语 1 Hive概述 Apache Hive是一个开源的数据仓库查询和分析工具,最初由Facebook开发&…...

springboot项目打包优化,将所有第三方包单独打包至lib目录
在pom.xml中配置以下代码,随后使用mvnw clean package打包 <build><plugins><plugin><groupId>org.springframework.boot</groupId><artifactId>spring-boot-maven-plugin</artifactId><configuration><!-- 主…...

使用 Ccrypt 在 Linux 中加密/解密文件
Ccrypt 是一个用于数据加密和解密的命令行工具。Ccrypt 基于 Rijndael 密码,与 AES 标准中使用的密码相同。另一方面,在 AES 标准中,使用 128 位块大小,而 ccrypt 使用 256 位块大小。Ccrypt 通常使用 .cpt 文件扩展名来表示加密文件。 它是一个轻量级的工具,该工具的安装…...

poi3.10 excel xls 设置列宽行高背景色加粗
poi excel xls格式 设置列宽行高背景色加粗HSSFWorkbook wb new HSSFWorkbook(); Sheet sheet wb.createSheet("sheet1");HSSFCellStyle style wb.createCellStyle(); style.setFillForegroundColor(IndexedColors.LIGHT_TURQUOISE.getIndex());//背景色 style.se…...

揭秘分布式文件系统大规模元数据管理机制——以Alluxio文件系统为例
作者简介: 辭七七,目前大,正在学习C/C,Java,Python等 作者主页: 七七的个人主页 文章收录专栏: 七七的闲谈 欢迎大家点赞 👍 收藏 ⭐ 加关注哦!💖Ὁ…...

微信小程序onReachBottom事件使用
在微信小程序中,onReachBottom事件用于监听页面滚动到页面底部的时候触发的事件。当用户滑动页面到底部时,可以通过监听该事件来执行相应的操作。 要使用onReachBottom事件,需要在对应的页面或组件中定义一个函数,并在Page或Comp…...

数据孤岛的突破口在哪里?
国务院于2021年12月发布的《“十四五”数字经济发展规划》中提到,我国数字经济发展中数字鸿沟问题未得到有效解决,各行业应充分发挥数据要素作用,加强数据治理和监管工作。“数据孤岛”问题虽早已被提出,但至今仍然存在࿰…...

【送书活动】全网超50万粉丝的Linux大咖良许,出书了!
前言 「作者主页」:雪碧有白泡泡 「个人网站」:雪碧的个人网站 「推荐专栏」: ★java一站式服务 ★ ★ React从入门到精通★ ★前端炫酷代码分享 ★ ★ 从0到英雄,vue成神之路★ ★ uniapp-从构建到提升★ ★ 从0到英雄ÿ…...
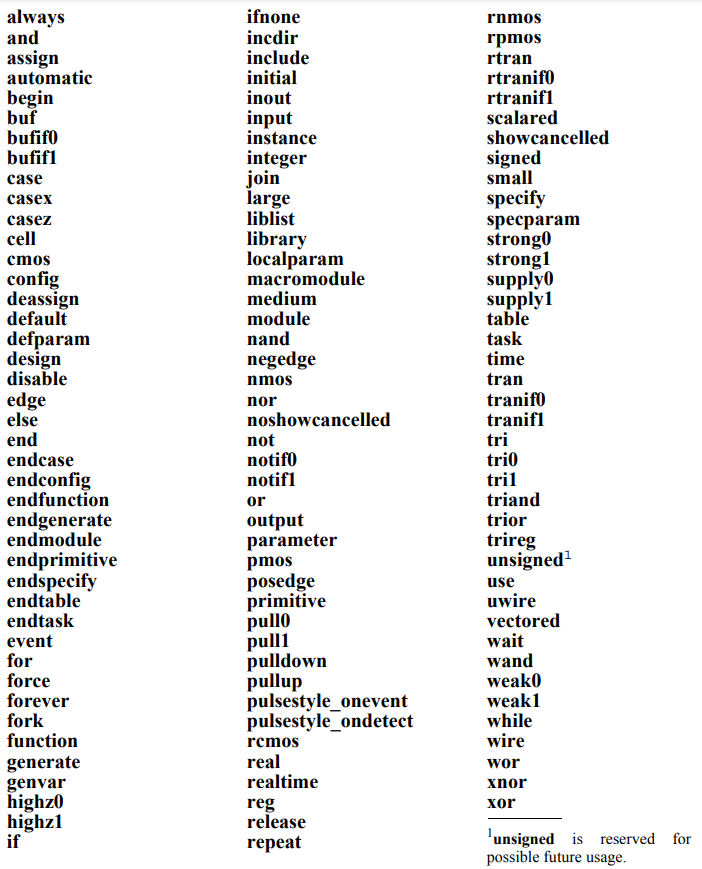
深入浅出学Verilog--基础语法
1、简介 Verilog的语法和C语言非常类似,相对来说还是非常好学的。和C语言一样,Verilog语句也是由一连串的令牌(Token)组成。1个令牌必须由1个或1个以上的字符(character)组成,令牌可以是&#x…...

基于Spring、SpringMVC、Mybatis的超市管理系统
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于SSM的超市订单管理系统,java项目。 …...

spring中的@Configuration配置类和@Component
在Spring的开发工作中,基本都会使用配置注解,尤其以Component及Configuration为主,当然在Spring中还可以使用其他的注解来标注一个类为配置类,这是广义上的配置类概念,但是这里我们只讨论Component和Configuration&…...
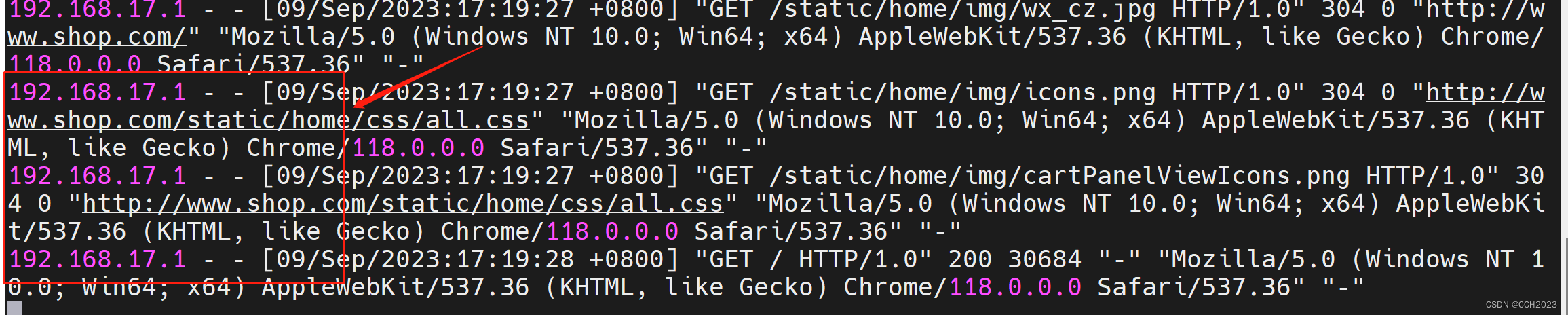
企业架构LNMP学习笔记29
Nginx负载均衡配置: 架构分析: 1)用户访问请求Nginx负载均衡服务器; 2)Nginx负载均衡服务器再分发请求到Web服务器。 实际配置负载均衡,只需修改作为负载均衡服务器的Nginx即可,当前架构中的…...

Ubuntu14.04离线安装gcc-5.3.0
离线安装gcc 下载gcc安装包下载相关依赖下载gmp下载mpfr下载mpc 编译、安装gcc配置环境变量 拉取的一个虚拟机使用的系统是Ubuntu14.04,gcc版本是4.8.4,由于gcc版本较低,不太支持Libtorch,于是搜寻了许多办法来解决这个问题&#…...
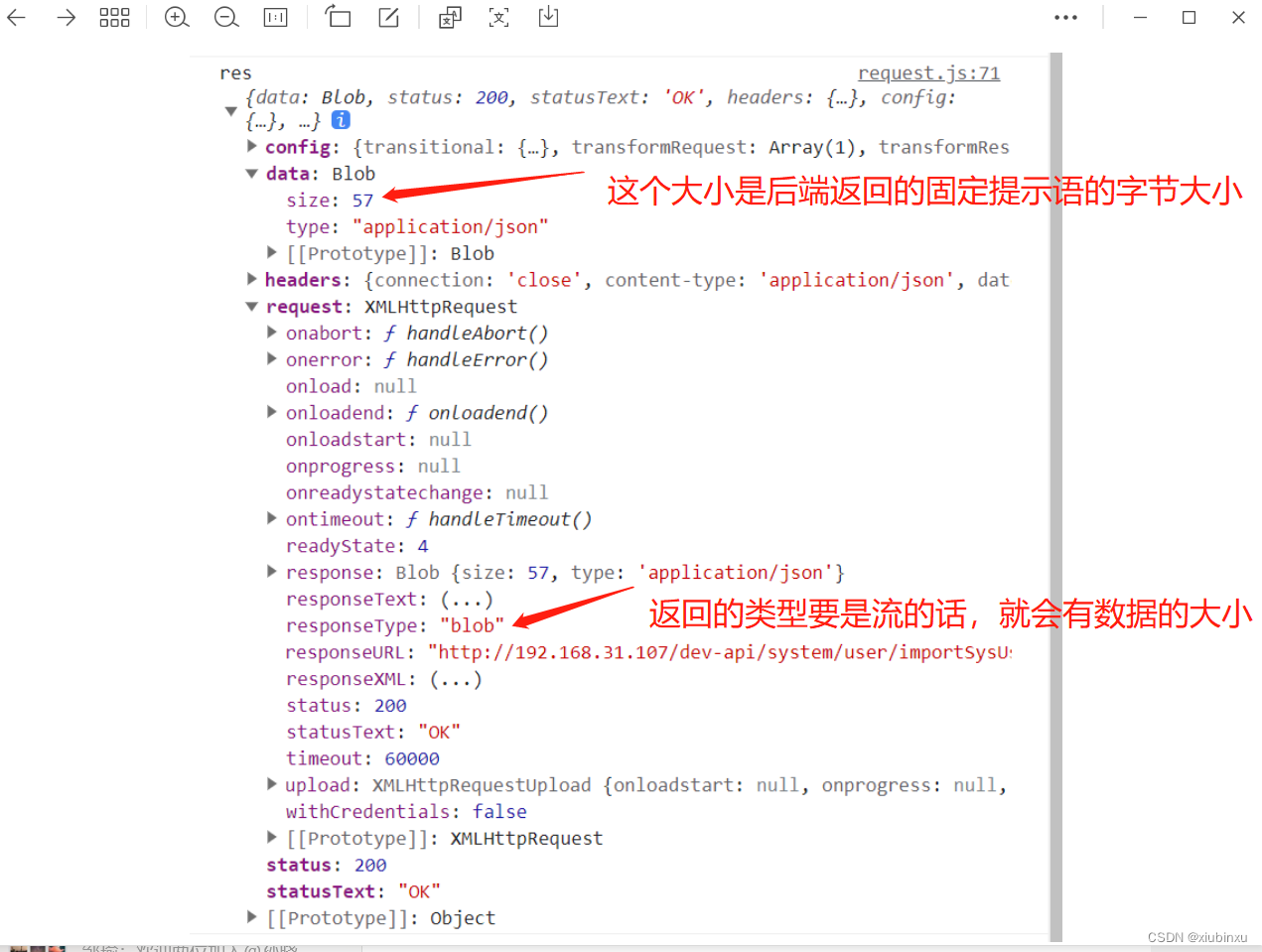
axios返回几种数据格式? 其中Blob返回时的size是什么意思?
axios返回几种数据格式? 其中Blob返回时的size是什么意思? 1、字符串(String):服务器可以返回纯文本或HTML内容,Axios会将其作为字符串返回。 2、JSON(JavaScript Object Notation)ÿ…...
【GO语言基础】基本数据类型
系列文章目录 【Go语言学习】ide安装与配置 【GO语言基础】前言 【GO语言基础】变量常量 【GO语言基础】数据类型 文章目录 系列文章目录数据类型数值型:整数类型:浮点数类型: 字符型-布尔型-字符串零值转义字符 常用类型转换运算符总结 数据…...

【Python】OpenCV立体相机配准与三角化代码实现
下面的介绍了使用python和OpenCV对两个相机进行标定、配准,同时实现人体关键点三角化的过程 import cv2 as cv import glob import numpy as np import matplotlib.pyplot as pltdef calibrate_camera(images_folder):images_names = glob.glob(images_folder...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...
