蓝桥杯官网练习题(李白打酒)
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
话说大诗人李白,一生好饮。幸好他从不开车。
一天,他提着酒壶,从家里出来,酒壶中有酒2斗。他边走边唱:
无事街上走,提壶去打酒。 逢店加一倍,遇花喝一斗。
这一路上,他一共遇到店5次,遇到花 1010 次,已知最后一次遇到的是花,他正好把酒喝光了。
请你计算李白遇到店和花的次序,可以把遇店记为 a,遇花记为 b 。则:babaabbabbabbbb 就是合理的次序。像这样的答案一共有多少呢?请你计算出所有可能方案的个数(包含题目给出的)。
运行限制
- 最大运行时间:1s
- 最大运行内存: 128M
import java.util.Scanner;public class Main {static int ans=0;public static void main(String[] args) {dfs(2,0,0);System.out.println(ans);}public static void dfs(int jiu,int dian,int hua){if(jiu==1&&dian==5&&hua==9){ //最后一次一定是花,如果jiu==0,hua==10会ans++; //出现很多种情况,不一定最后一次是花}if(dian<5){dfs(jiu*2,dian+1,hua);}if(hua<10){dfs(jiu-1,dian,hua+1);}}
}相关文章:
)
蓝桥杯官网练习题(李白打酒)
题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 话说大诗人李白,一生好饮。幸好他从不开车。 一天,他提着酒壶,从家里出来,酒壶中有酒2斗。他边走边唱: …...
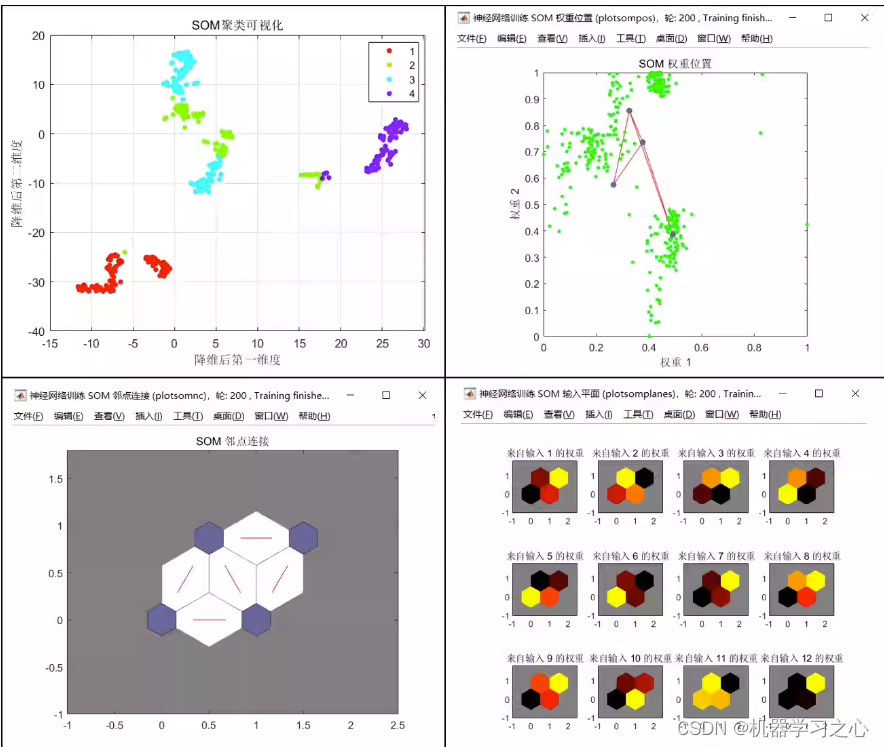
聚类分析 | MATLAB实现基于SOM自组织特征映射聚类可视化
聚类分析 | MATLAB实现基于SOM自组织特征映射聚类可视化 目录 聚类分析 | MATLAB实现基于SOM自组织特征映射聚类可视化效果一览基本介绍程序设计参考资料 效果一览 基本介绍 基于自组织特征映射聚类算法(SOM)的数据聚类可视化 可直接运行 注释清晰 Matlab语言 1.多特征输入&…...

Spring AOP:面向切面编程在实际项目中的应用
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

python爬虫的反扒技术有哪些如何应对
Python爬虫常见的反扒技术主要有以下几种: IP封禁:有些网站会限制爬虫的IP访问频率,如果访问流量过大,可能会被封禁IP。可以通过使用代理IP或者轮换IP的方式规避此类反扒技术。 用户代理限制:有些网站会通过检测请求头中的用户代…...
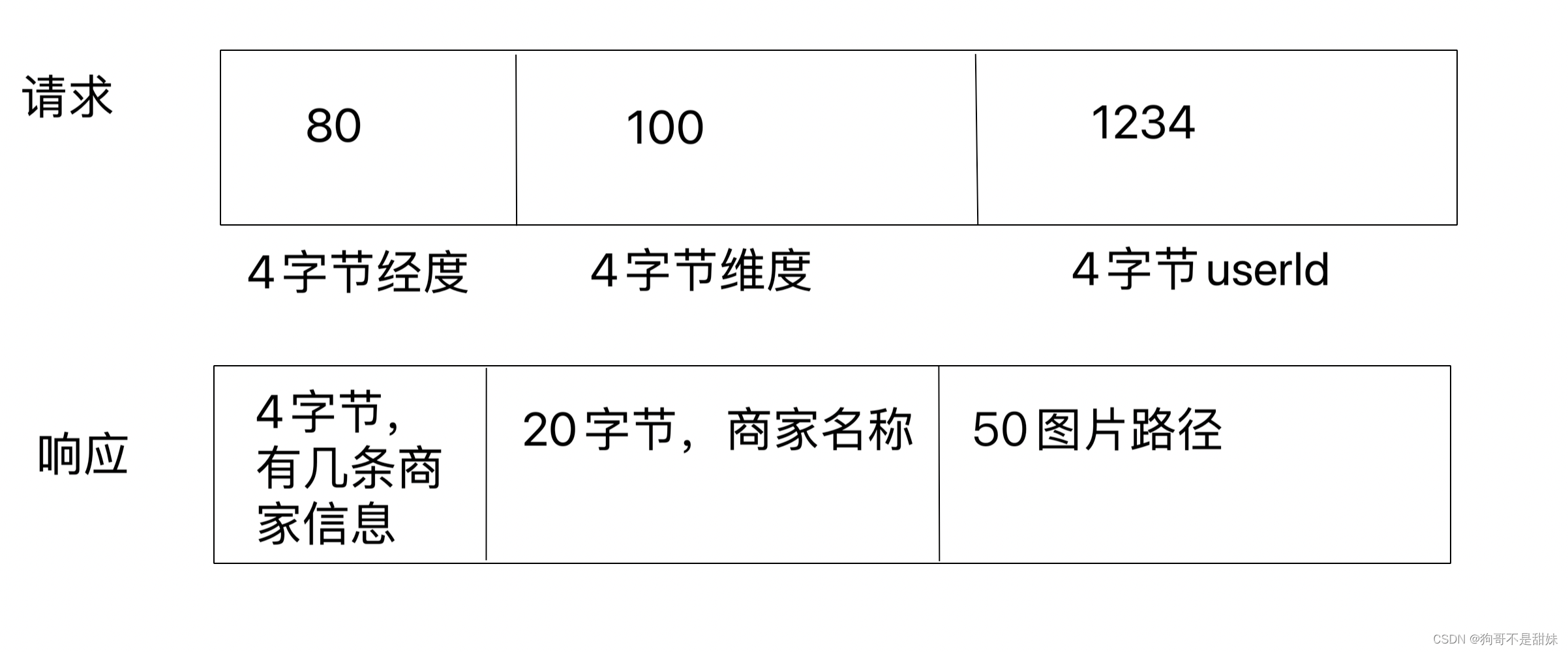
网络原理,了解xml, json,protobuffer的特点
目录 外卖服务器场景带入 大佬们通用的规范格式 一、👦 外卖服务器场景 外面服务器沟通有很多模式——展示商家列表等等,只是其中一个,因此需要一个统一的规划了——不同应用程序,里面的自定义格式是不一样的,这样的…...
工具 | XShell的学习与使用
工具 | XShell的学习与使用 时间:2023年9月8日09:03:29 文章目录 工具 | XShell的学习与使用1.下载2.安装 1.下载 1.官网XSHELL - NetSarang Website 2.免费版下载:家庭/学校免费 - NetSarang Website (xshell.com) 3.https://cdn.netsarang.net/de06d10…...
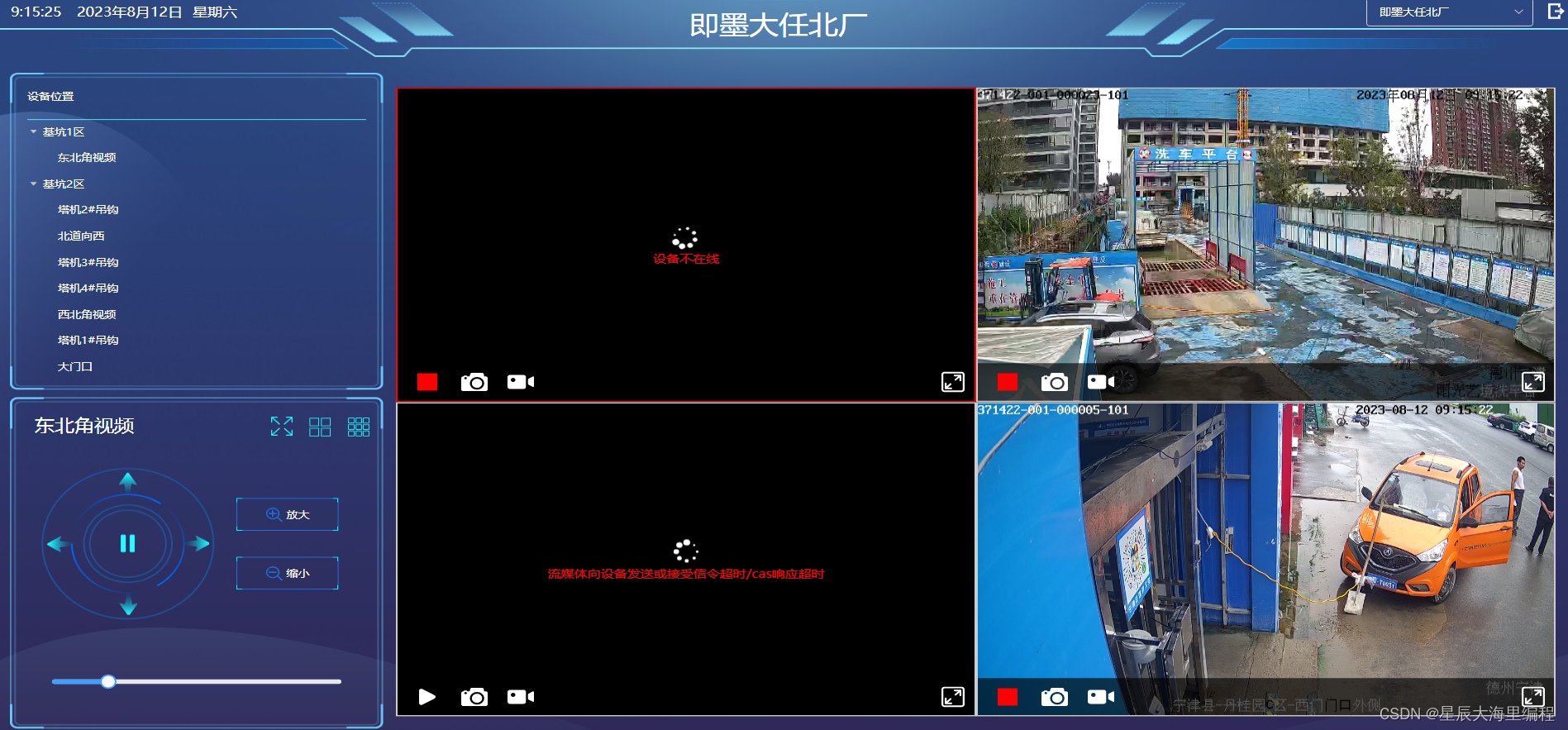
基于微服务+Java+Spring Cloud +UniApp +MySql开发的智慧工地源码(物联网、人工智能、AI识别、危大工程)
智慧工地系统利用物联网、人工智能、云计算、大数据、移动互联网等新一代信息技术,通过工地中台、三维建模服务、视频AI分析服务等技术支撑,实现智慧工地高精度动态仿真,趋势分析、预测、模拟,建设智能化、标准化的智慧工地综合业…...

Kafka安装与使用
Kafka是一种高吞吐量的分布式发布订阅消息系统,因为其高吞吐量、分布式可扩展性等等强大功能使得在目前互联网系统中广泛使用。该篇博客入门了解一下Kafka的安装及使用。 Kafka概念 Kafk是分布式消息队列。Kafka对消息保存时根据Topic进行归类,发送消息…...

php出现SSL certificate problem: unable to get local issuer certificate的解决办法
当在本地使用curl或者一些其它封装好的http类库或组件(如php界 知名的 http客户端 Guzzle)需要访问https时,如果本地没有配置证书,会出现SSL certificate problem: unable to get local issuer certificate的报错信息。 解决办法一…...

Flask狼书笔记 | 07_留言板
文章目录 7 留言板7.1 使用包组织代码7.2 Web开发流程7.3 使用Bootstrap-Flask7.4 Flask-Moment本地化日期和时间7.5 使用Faker生成虚拟数据7.6 Flask_DebugToolbar调试程序7.7 Flask配置的两种组织形式小结 7 留言板 这是一个简单的程序,涉及到的大部分是之前所学…...

文件导入之Validation校验List对象数组
背景: 我们的接口是一个List对象,对象里面的数据基本都有一些基础数据校验的注解,我们怎么样才能校验这些基础规则呢? 我们在导入excel文件进行数据录入的时候,数据录入也有基础的校验规则,这个时候我们又…...
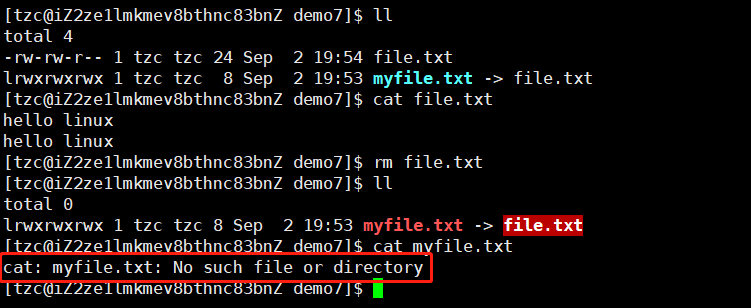
【Linux】文件系统
磁盘及文件系统 文件的增删查改 重新认识目录 目录是文件嘛? 是的。 目录有iNode嘛? 有 目录有内容嘛? 有 任何一个文件,一定在一个目录内部,所以一个目录的内容是什么? 需要数据块,目录的数据…...
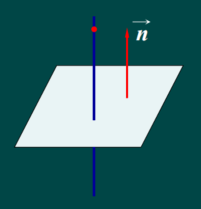
1.5 空间中的平面与直线
空间中的平面和直线 知识点1 平面方程 1.平面的法向量与法式 定义1 若向量n 垂直与平面N,则称向量n为平面N的法向量。 设一平面通过一直点 M 0 ( x 0 , y 0 , z 0 ) M_0(x_0,y_0,z_0) M0(x0,y0,z0)求垂直于非零向量 n ⃗ \vec{n} n (A,B,C),求改平面N的…...
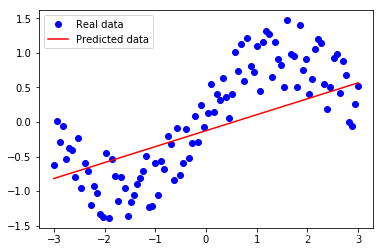
【深度学习】实验06 使用TensorFlow完成线性回归
文章目录 使用TensorFlow完成线性回归1. 导入TensorFlow库2. 构造数据集3. 定义基本模型4. 训练模型5. 线性回归图 附:系列文章 使用TensorFlow完成线性回归 TensorFlow是由Google开发的一个开源的机器学习框架。它可以让开发者更加轻松地构建和训练深度学习模型&a…...
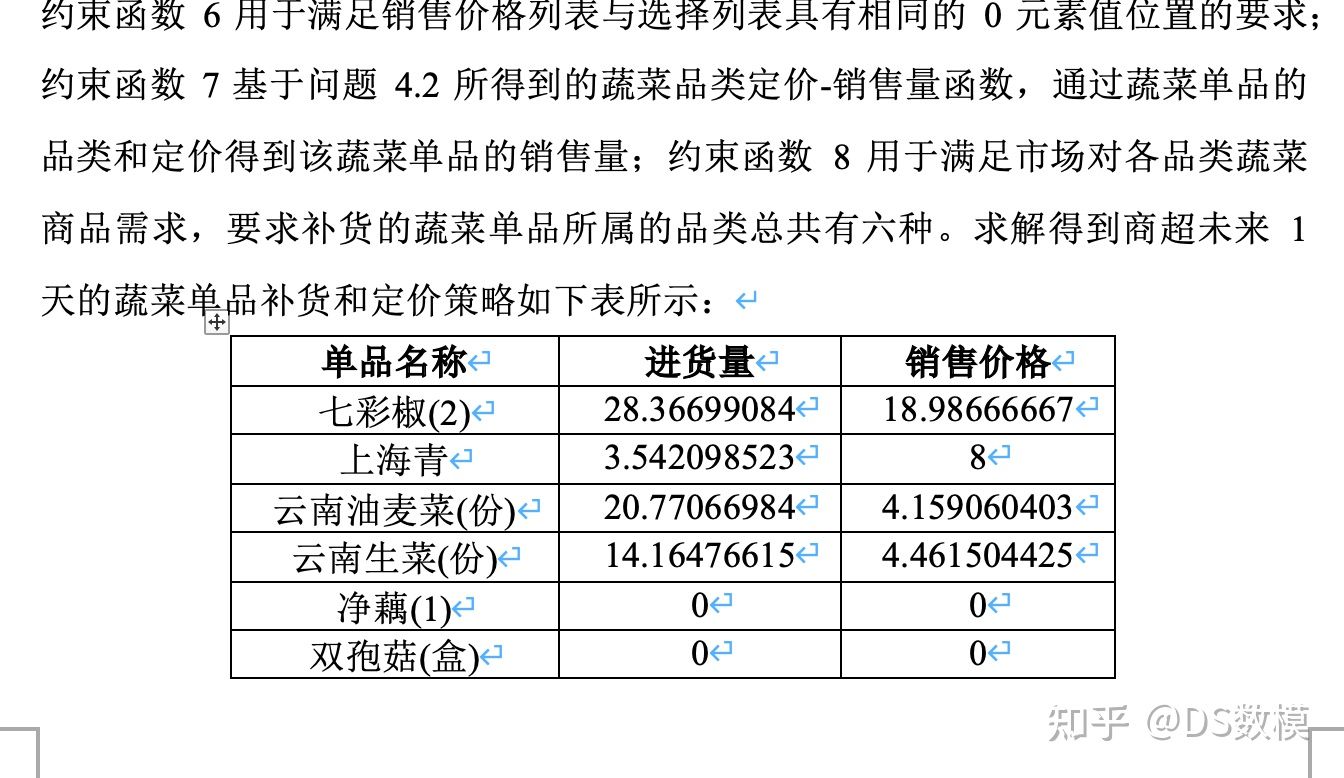
2023国赛 C题论文 蔬菜类商品自动定价与补货策略
因为一些不可抗力,下面仅展示小部分论文,其余看文末 一、问题重述 在生鲜超市管理领域,涉及一系列复杂问题,包括供应链管理、定价策略以及市场需求分析等方面。以蔬菜类商品为案例,这些商品在生鲜商超中具有较短的保…...
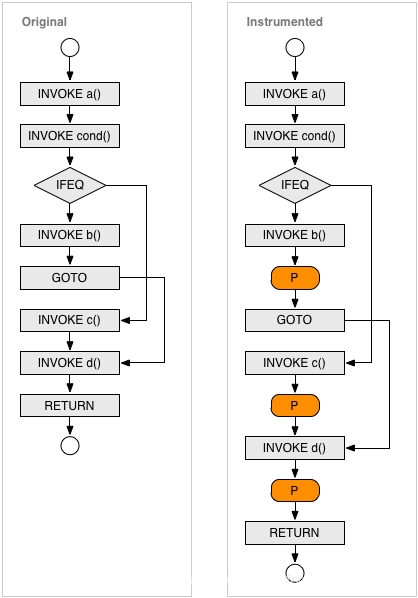
使用 【jacoco】对基于 SpringBoot 和 Dubbo RPC 的项目生成测试覆盖率报告:实践+原理
基于 Dubbo RPC 的项目中有一个提供者项目backend、一个消费者项目gateway、以及注册中心nacos。本篇文章记录在windows本地对该框架的测试过程,以及介绍jacoco的基本原理 测试过程 官网下载安装包解压到本地,https://www.jacoco.org/jacoco/ 只需要用…...

Mac OS合集
MacOS 10.15os 提取码:u12a 如不能点击跳转请复制此链接到浏览器:https://pan.baidu.com/s/1UgPNYprBgJrc25v5ushWxQ?pwdu12a MacOS 11.0 提取码:y77y 如不能点击跳转请复制此链接到浏览器打开:https://pan.baidu.com/s/1srmibmCi2T7UVGvHkCzGKA?pwdy7…...

算法之位运算
前言 位运算在我们的学习中占有很重要的地位,从二进制中数的存储等都需要我们进行位运算 一、位运算复习 1.位运算复习 按位与(&):如果两个相应的二进制位都为1,则该位的结果值才为1,否则为0 按位或( | ):如果…...
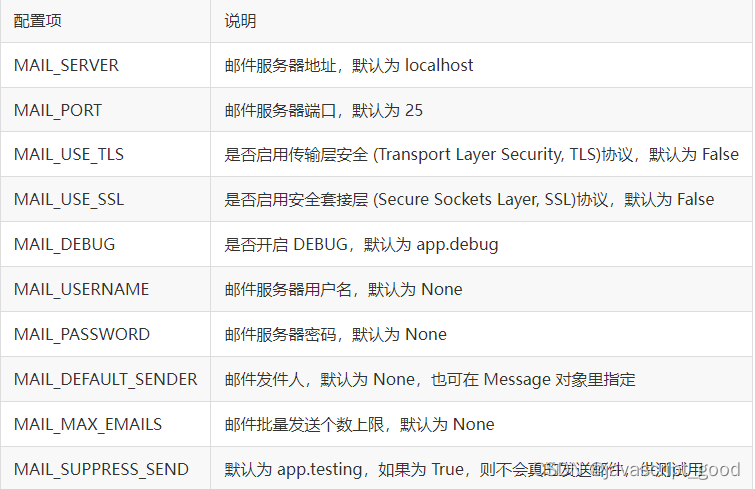
flask使用Flask-Mail实现邮件发送
Flask-Mail可以实现邮件的发送,并且可以和 Flask 集成,让我们更方便地实现此功能。 1、安装 使用pip安装: $ pip install Flask-Mail或下载源码安装: $ git clone https://github.com/mattupstate/flask-mail.git $ cd flask-…...
React refers to UMD global, but the current file is a module vite初始化react项目
vite搭建react项目 初始化项目 npm create vite 在执行完上面的命令后,npm 首先会自动下载create-vite这个第三方包,然后执行这个包中的项目初始化逻辑。输入项目名称之后按下回车,此时需要选择构建的前端框架: ✔ Project na…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
