数据结构与算法(三):栈与队列
上一篇《数据结构与算法(二):线性表》中介绍了数据结构中线性表的两种不同实现——顺序表与链表。这一篇主要介绍线性表中比较特殊的两种数据结构——栈与队列。首先必须明确一点,栈和队列都是线性表,它们中的元素都具有线性关系,即前驱后继关系。
一、栈
1、基本概念
栈(也称下压栈,堆栈)是仅允许在表尾进行插入和删除操作的线性表。我们把允许插入和删除的一端称为栈顶(top),另一端称为栈底(bottom)。栈是一种后进先出(Last In First Out)的线性表,简称(LIFO)结构。栈的一个典型应用是在集合中保存元素的同时颠倒元素的相对顺序。
抽象数据类型:
栈同线性表一样,一般包括插入、删除等基本操作。其基于泛型的API接口代码如下:
public interface Stack<E> {//栈是否为空boolean isEmpty();//栈的大小int size();//入栈void push(E element);//出栈E pop();//返回栈顶元素E peek();
}
栈的实现通常有两种方式:
- 基于数组的实现(顺序存储)
- 基于链表的实现(链式存储)
2、栈的顺序存储结构
栈的顺序存储结构其实是线性表顺序存储结构的简化,我们可以简称它为「顺序栈」。其存储结构如下图:
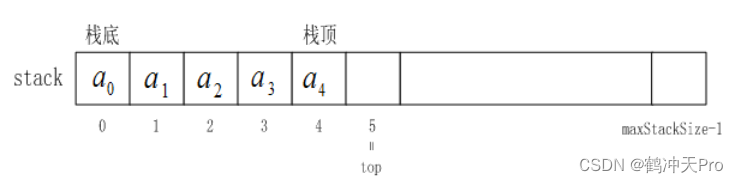
实现代码如下:
import java.util.Iterator;
/*** 能动态调整数组大小的栈*/
public class ArrayStack<E> implements Iterable<E>, Stack<E> {private E[] elements;private int size=0;@SuppressWarnings("unchecked")public ArrayStack() {elements = (E[])new Object[1]; //注意:java不允许创建泛型数组}@Override public int size() {return size;}@Override public boolean isEmpty() {return size == 0;}//返回栈顶元素@Override public E peek() {return elements[size-1];}//调整数组大小public void resizingArray(int num) {@SuppressWarnings("unchecked")E[] temp = (E[])new Object[num];for(int i=0;i<size;i++) {temp[i] = elements[i];}elements = temp;}//入栈@Override public void push(E element) {if(size == elements.length) {resizingArray(2*size);//若数组已满将长度加倍}elements[size++] = element;}//出栈@Override public E pop() {E element = elements[--size];elements[size] = null; //注意:避免对象游离if(size > 0 && size == elements.length/4) {resizingArray(elements.length/2);//小于数组1/4,将数组减半}return element;}//实现迭代器, Iterable接口在java.lang中,但Iterator在java.util中public Iterator<E> iterator() {return new Iterator<E>() {private int num = size;public boolean hasNext() {return num > 0;}public E next() {return elements[--num];}};}//测试public static void main(String[] args) {int[] a = {1,2,3,4,new Integer(5),6};//测试数组ArrayStack<Integer> stack = new ArrayStack<Integer>();System.out.print("入栈顺序:");for(int i=0;i<a.length;i++) {System.out.print(a[i]+" ");stack.push(a[i]);}System.out.println();System.out.print("出栈顺序数组实现:");//迭代for (Integer s : stack) {System.out.print(s+" ");}}
}
优点:
- 每项操作的用时都与集合大小无关
- 空间需求总是不超过集合大小乘以一个常数
缺点:
- push()和pop()操作有时会调整数组大小,这项操作的耗时和栈的大小成正比
3、两栈共享空间
用一个数组来存储两个栈,让一个栈的栈底为数组的始端,即下标为0,另一个栈的栈底为数组的末端,即下标为 n-1。两个栈若增加元素,栈顶都向中间延伸。其结构如下:
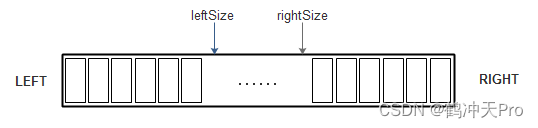
这种结构适合两个栈有相同的数据类型并且空间需求具有相反的关系的情况,即一个栈增长时另一个栈缩短。如,买股票,有人买入,就一定有人卖出。
代码:
public class SqDoubleStack<E> {private static final int MAXSIZE = 20;private E[] elements;private int leftSize=0;private int rightSize= MAXSIZE - 1;//标记是哪个栈enum EnumStack {LEFT, RIGHT}@SuppressWarnings("unchecked")public SqDoubleStack() {elements = (E[])new Object[MAXSIZE]; //注意:java不允许创建泛型数组}//入栈public void push(E element, EnumStack es) {if(leftSize - 1 == rightSize)throw new RuntimeException("栈已满,无法添加"); if(es == EnumStack.LEFT) {elements[leftSize++] = element;} else {elements[rightSize--] = element;}}//出栈public E pop(EnumStack es ) {if(es == EnumStack.LEFT) {if(leftSize <= 0)throw new RuntimeException("栈为空,无法删除"); E element = elements[--leftSize];elements[leftSize] = null; //注意:避免对象游离return element;} else {if(rightSize >= MAXSIZE - 1)throw new RuntimeException("栈为空,无法删除"); E element = elements[++rightSize];elements[rightSize] = null; //注意:避免对象游离return element;}}//测试public static void main(String[] args) {int[] a = {1,2,3,4,new Integer(5),6};//测试数组SqDoubleStack<Integer> stack = new SqDoubleStack<Integer>();System.out.print("入栈顺序:");for(int i=0;i<a.length;i++) {System.out.print(a[i]+" ");stack.push(a[i], EnumStack.RIGHT);}System.out.println();System.out.print("出栈顺序数组实现:");//迭代for(int i=0;i<a.length;i++) {System.out.print(stack.pop(EnumStack.RIGHT)+" ");}}
}
4、栈的链式存储结构
栈的链式存储结构,简称链栈。为了操作方便,一般将栈顶放在单链表的头部。通常对于链栈来说,不需要头结点。
其存储结构如下图:

代码实现如下:
import java.util.Iterator;
public class LinkedStack<E> implements Stack<E>, Iterable<E> {private int size = 0;private Node head = null;//栈顶private class Node {E element;Node next;Node(E element, Node next) {this.element = element;this.next = next;}}@Override public int size() {return size;}@Override public boolean isEmpty() {return size == 0;}@Override public E peek() {return head.element;}@Override public void push(E element) {Node node = new Node(element, head);head = node;size++;}@Override public E pop() {E element = head.element;head = head.next;size--;return element;}//迭代器public Iterator<E> iterator() {return new Iterator<E>() {private Node current = head;public boolean hasNext() {return current != null;}public E next() {E element = current.element;current = current.next;return element;}};}public static void main(String[] args) {int[] a = {1,2,3,4,new Integer(5),6};//测试数组LinkedStack<Integer> stack = new LinkedStack<Integer>();System.out.print("入栈顺序:");for(int i=0;i<a.length;i++) {System.out.print(a[i]+" ");stack.push(a[i]);}System.out.println();System.out.print("出栈顺序链表实现:");for (Integer s : stack) {System.out.print(s+" ");}}
}
注意:私有嵌套类(内部类Node)的一个特点是只有包含他的类能够直接访问他的实例变量,无需将他的实例变量(element)声明为public或private。即使将变量element声明为private,外部类依然可以通过Node.element的形式调用。
优点:
- 所需空间和集合的大小成正比
- 操作时间和集合的大小无关
- 链栈的push和pop操作的时间复杂度都为 O(1)。
缺点:
- 每个元素都有指针域,增加了内存的开销。
顺序栈与链栈的选择和线性表一样,若栈的元素变化不可预料,有时很大,有时很小,那最好使用链栈。反之,若它的变化在可控范围内,使用顺序栈会好一些。
5、栈的应用——递归
栈的一个最重要的应用就是递归。那么什么是递归呢?借用《哥德尔、艾舍尔、巴赫——集异璧之大成》中的话:
递归从狭义上来讲,指的是计算机科学中(也就是像各位程序猿都熟悉的那样),一个模块的程序在其内部调用自身的技巧。如果我们把这个效果视觉化就成为了「德罗斯特效应」,即图片的一部分包涵了图片本身。
如下面这张图,「先有书还是先有封面 ?」

我们把一个直接调用自身或通过一系列语句间接调用自身的函数,称为递归函数。每个递归函数必须至少有一个结束条件,即不在引用自身而是返回值退出。否则程序将陷入无穷递归中。
一个递归的例子:斐波那契数列(Fibonacci)
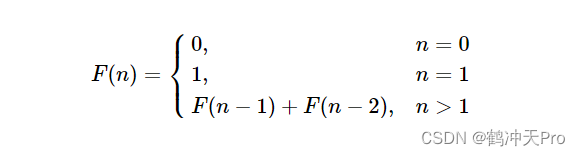
递归实现:
public int fibonacci(int num) {if(num < 2)return num == 0 ? 0 : 1;return fibonacci(num - 1) + fibonacci(num - 2);
}
迭代实现:
public int fibonacci(int num) {if(num < 2)return num == 0 ? 0 : 1;int temp1 = 0;int temp2 = 1;int result = 0;for(int i=2; i < num; i++) {result = temp1 + temp2;temp1 = temp2;temp2 = result;}return result;
}
迭代与递归的区别:
- 迭代使用的是循环结构,递归使用的是选择结构。
- 递归能使程序的结构更清晰、简洁,更容易使人理解。但是大量的递归将消耗大量的内存和时间。
编译器使用栈来实现递归。在前行阶段,每一次递归,函数的局部变量、参数值及返回地址都被压入栈中;退回阶段,这些元素被弹出,以恢复调用的状态。
二、队列
1、基本概念
队列是只允许在一端进行插入操作,在另一端进行删除操作的线性表。它是一种基于先进先出(First In First Out,简称FIFO)策略的集合类型。允许插入的一端称为队尾,允许删除的一端称为队头。
抽象数据类型:
队列作为一种特殊的线性表,它一样包括插入、删除等基本操作。其基于泛型的API接口代码如下:
public interface Queue<E> {//队列是否为空boolean isEmpty();//队列的大小int size();//入队void enQueue(E element);//出队E deQueue();
}
同样的,队列具有两种存储方式:顺序存储和链式存储。
2、队列的顺序存储结构
其存储结构如下图:

与栈不同的是,队列元素的出列是在队头,即下表为0的位置。为保证队头不为空,每次出队后队列中的所有元素都得向前移动,此时时间复杂度为 O(n)。此时队列的实现和线性表的顺序存储结构完全相同,不在详述。
若不限制队列的元素必须存储在数组的前n个单元,出队的性能就能大大提高。但这种结构可能产生「假溢出」现象,即数组末尾元素已被占用,如果继续向后就会产生下标越界,而前面为空。如下图:
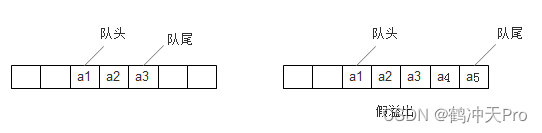
解决「假溢出」的办法就是若数组未满,但后面满了,就从头开始入队。我们把这种逻辑上首尾相连的顺序存储结构称为循环队列。
数组实现队列的过程:
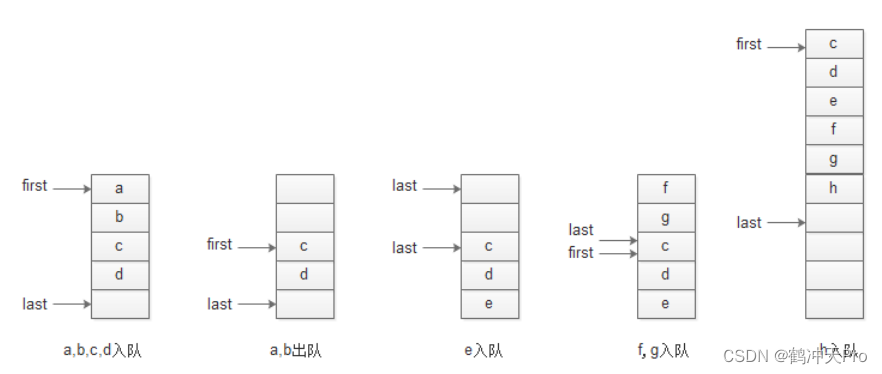
假设开始时数组长度为5,如图,当f入队时,此时数组末尾元素已被占用,如果继续向后就会产生下标越界,但此时数组未满,将从头开始入队。当数组满(h入队)时,将数组的长度加倍。
代码如下:
import java.util.Iterator;
/*** 能动态调整数组大小的循环队列*/
public class CycleArrayQueue<E> implements Queue<E>, Iterable<E> {private int size; //记录队列大小private int first; //first表示头元素的索引private int last; //last表示尾元素后一个的索引private E[] elements;@SuppressWarnings("unchecked")public CycleArrayQueue() {elements = (E[])new Object[1];}@Override public int size() {return size;}@Override public boolean isEmpty(){return size == 0;}//调整数组大小public void resizingArray(int num) {@SuppressWarnings("unchecked")E[] temp = (E[])new Object[num];for(int i=0; i<size; i++) {temp[i] = elements[(first+i) % elements.length];}elements = temp;first = 0;//数组调整后first,last位置last = size;}@Override public void enQueue(E element){//当队列满时,数组长度加倍if(size == elements.length) resizingArray(2*size);elements[last] = element;last = (last+1) % elements.length;//【关键】size++;}@Override public E deQueue() {if(isEmpty()) return null;E element = elements[first];first = (first+1) % elements.length;//【关键】size--;//当队列长度小于数组1/4时,数组长度减半if(size > 0 && size < elements.length/4) resizingArray(2*size);return element;}//实现迭代器public Iterator<E> iterator() {return new Iterator<E>() {private int num = size;private int current = first;public boolean hasNext() {return num > 0;}public E next() {E element = elements[current++];num--;return element;} };}public static void main(String[] args) {int[] a = {1,2,4,6,new Integer(10),5};CycleArrayQueue<Integer> queue = new CycleArrayQueue<Integer>();for(int i=0;i<a.length;i++) {queue.enQueue(a[i]);System.out.print(a[i]+" ");} System.out.println("入队");for (Integer s : queue) {System.out.print(s+" ");}System.out.println("出队");}
}
3、队列的链式存储结构
队列的链式存储结构,其实就是线性表的单链表,只不过它只能尾进头出而已,我们简称为「链队列」。
存储结构如下图:
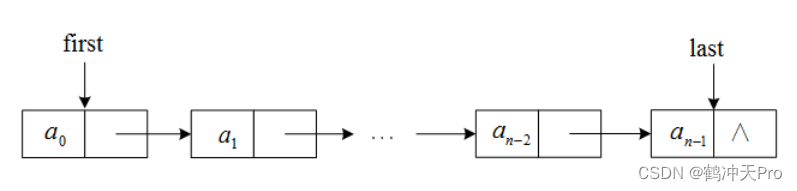
代码如下:
import java.util.Iterator;
/*** 队列的链式存储结构,不带头结点的实现*/
public class LinkedQueue<E> implements Queue<E>, Iterable<E> {private Node first; //头结点private Node last; //尾结点private int size = 0;private class Node {E element;Node next;Node(E element) {this.element = element;}}@Override public int size() {return size;}@Override public boolean isEmpty(){return size == 0;}//入队@Override public void enQueue(E element) {Node oldLast = last;last = new Node(element);if(isEmpty()) {first = last;//【要点】}else {oldLast.next = last;}size++;}//出队@Override public E deQueue() {E element = first.element;first = first.next;size--;if(isEmpty()) last = null;//【要点】return element;}//实现迭代器public Iterator<E> iterator() {return new Iterator<E>() {private Node current = first;public boolean hasNext() {return current != null;}public E next(){E element = current.element;current = current.next;return element;}};}public static void main(String[] args) {int[] a = {1,2,4,6,new Integer(10),5};LinkedQueue<Integer> queue = new LinkedQueue<Integer>();for(int i=0;i<a.length;i++) {queue.enQueue(a[i]);System.out.print(a[i]+" ");} System.out.println("入队");for (Integer s : queue) {System.out.print(s+" ");}System.out.println("出队");}
}
循环队列与链队列,它们的基本操作的时间复杂度都为 O(1)。和线性表相同,在可以确定队列长度的情况下,建议使用循环队列;无法确定队列长度时使用链队列。
三、总结
栈与队列,它们都是特殊的线性表,只是对插入和删除操作做了限制。栈限定仅能在栈顶进行插入和删除操作,而队列限定只能在队尾插入,在队头删除。它们都可以使用顺序存储结构和链式存储结构两种方式来实现。
对于栈来说,若两个栈数据类型相同,空间需求相反,则可以使用共享数组空间的方法来实现,以提高空间利用率。对于队列来说,为避免插入删除操作时数据的移动,同时避免「假溢出」现象,引入了循环队列,使得队列的基本操作的时间复杂度降为 O(1)。
相关文章:

数据结构与算法(三):栈与队列
上一篇《数据结构与算法(二):线性表》中介绍了数据结构中线性表的两种不同实现——顺序表与链表。这一篇主要介绍线性表中比较特殊的两种数据结构——栈与队列。首先必须明确一点,栈和队列都是线性表,它们中的元素都具…...

Spring架构篇--2.5.2 远程通信基础Select 源码篇--window--sokcet.register
前言:通过Selector.open() 获取到Selector 的选择器后,服务端和客户的socket 都可以通过register 进行socker 的注册; 服务端 ServerSocketChannel 的注册: ServerSocketChannel serverSocketChannel ServerSocketChannel.open(…...
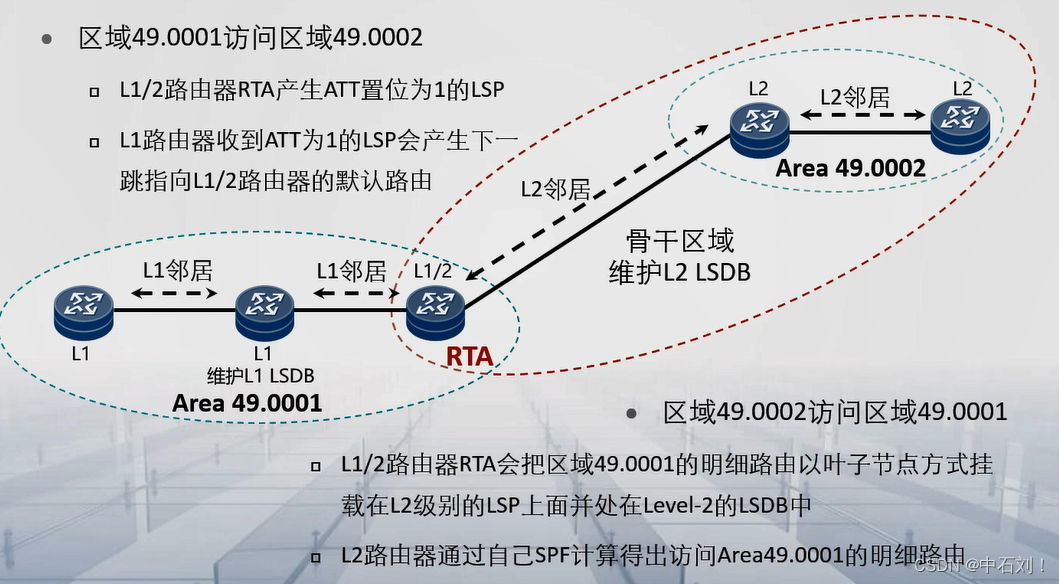
ISIS协议
ISIS协议基础简介应用场景路由计算过程地址结构路由器分类邻居Hello报文邻居关系建立DIS及DIS与DR的类比链路状态信息的载体链路状态信息的交互路由算法网络分层路由域区域间路由简介…...

CRM系统哪种品牌的好?这五款简单好用!
CRM系统哪种品牌的好?这五款简单好用! CRM系统是指利用软件、硬件和网络技术,为企业建立一个客户信息收集、管理、分析和利用的信息系统。CRM系统的基础功能主要包括营销自动化、客户管理、销售管理、客服管理、报表分析等,选择合…...
QT_dbus(ipc进程间通讯)
QT_dbus(ipc进程间通讯) 前言: 参考链接: https://www.cnblogs.com/brt3/p/9614899.html https://blog.csdn.net/weixin_43246170/article/details/120994311 https://blog.csdn.net/kchmmd/article/details/118605315 一个大型项目可能需要多个子程序同…...

华为OD机试 - 数组排序(C++) | 附带编码思路 【2023】
刷算法题之前必看 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD 清单查看地址:https://blog.csdn.net/hihell/category_12199283.html 华为OD详细说明:https://dream.blog.csdn.net/article/details/128980730 华为OD机试题…...
字符串转换为二进制-课后程序(JAVA基础案例教程-黑马程序员编著-第五章-课后作业)
【案例5-4】 字符串转换为二进制 【案例介绍】 1.任务描述 本例要求编写一个程序,从键盘录入一个字符串,将字符串转换为二进制数。在转换时,将字符串中的每个字符单独转换为一个二进制数,将所有二进制数连接起来进行输出。 案…...
SpringIOC
一、为什么要使用Spring? Spring 是个java企业级应用的开源开发框架。Spring主要用来开发Java应用,但是有些扩展是针对构建J2EE平台的web应用。Spring 框架目标是简化Java企业级应用开发,并通过POJO为基础的编程模型促进良好的编程习惯。 为…...

Debezium系列之:基于数据库信号表和Kafka信号Topic两种技术方案实现增量快照incremental技术的详细步骤
Debezium系列之:基于数据库信号表和Kafka信号Topic两种技术方案实现增量快照incremental技术的详细步骤 一、需求背景二、增量快照技术实现的两种方案三、基于数据库信号表实现增量快照技术的原理1.基于水印的快照2.信令表3.增量快照4.连接起重启四、基于数据库信号表实现增量…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 第 K 个最小码值的字母(Python) | 机试题+算法思路+考点+代码解析 【2023】
第 K 个最小码值的字母 题目 输入一个由n个大小写字母组成的字符串 按照 ASCII 码值从小到大进行排序 查找字符串中第k个最小 ASCII 码值的字母(k>=1) 输出该字母所在字符串中的位置索引(字符串的第一个位置索引为 0) k如果大于字符串长度则输出最大 ASCII 码值的字母所在…...
PointNet++训练自己的数据集(附源码)
本文针对PointNet强大的三维点云分类功能,详细讲解怎么训练自己的数据集,在此之前,需要确保已经能够跑通源码的训练和测试,如果没有,请参考PointNet的源码运行。数据放置1.1. 在mytensor_shape_names.txt中配置自己的分…...
ROS2可视化利器---Foxglove Studio
0. 简介 之前作者已经讲了《ROS1可视化利器—Webviz》,然后就有读者问,ROS2有没有可以使用的可视化工具呢,答案是肯定的,除了plotjuggler这种ROS1和ROS2通用的可视化利器,还有一种全平台通用的软件FoxgloveStudio&…...
)
python实战应用讲解-【语法基础篇】流程控制-控制流的元素及语句(附示例代码)
目录 控制流的元素 条件 代码块 程序执行 代码块嵌套 控制流语句 if 语句...

[蓝桥杯 2019 省 A] 外卖店优先级
蓝桥杯 2019 年省赛 A 组 G 题题目描述“饱了么”外卖系统中维护着 N家外卖店,编号 1 ∼ N。每家外卖店都有一个优先级,初始时 (0 时刻)优先级都为0。每经过 1 个时间单位,如果外卖店没有订单,则优先级会减少 1&#x…...
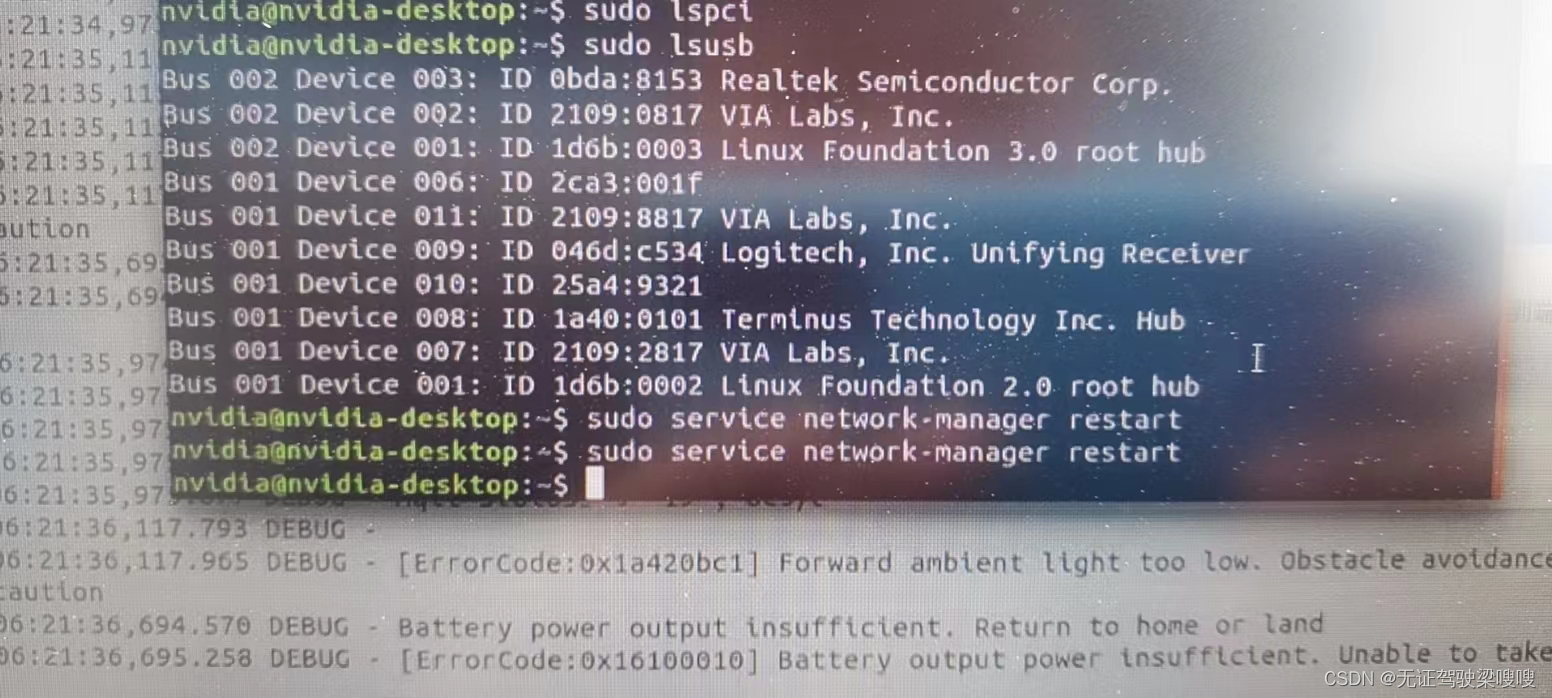
Jetson Xavier nx(ubuntu18.04)安装rtl8152网卡驱动和8192网卡驱动
含义 Bus 002 : 指明设备连接到哪条总线。 Device 003 : 表明这是连接到总线上的第二台设备。 ID : 设备的ID,包括厂商的ID和产品的ID,格式 厂商ID:产品ID。 Realtek Semiconductor Corp. RTL8153 Gigabit Ethernet Adapter:生产商名字和设备…...

Rocky 9.1操作系统实现zabbix6.0的安装部署实战
文章目录前言一. 实验环境二. 安装zabbix过程2.1. 安装zabbix源2.2 安装zabbix相关的软件2.3 安装数据库并启动2.4 开始初始化数据库:2.5 创建数据库实例及对应的用户2.6 导入官网提供的数据2.7 配置zabbix 服务的配置文件2.8. 启动服务2.9 从网页进行安装2.10 登陆…...
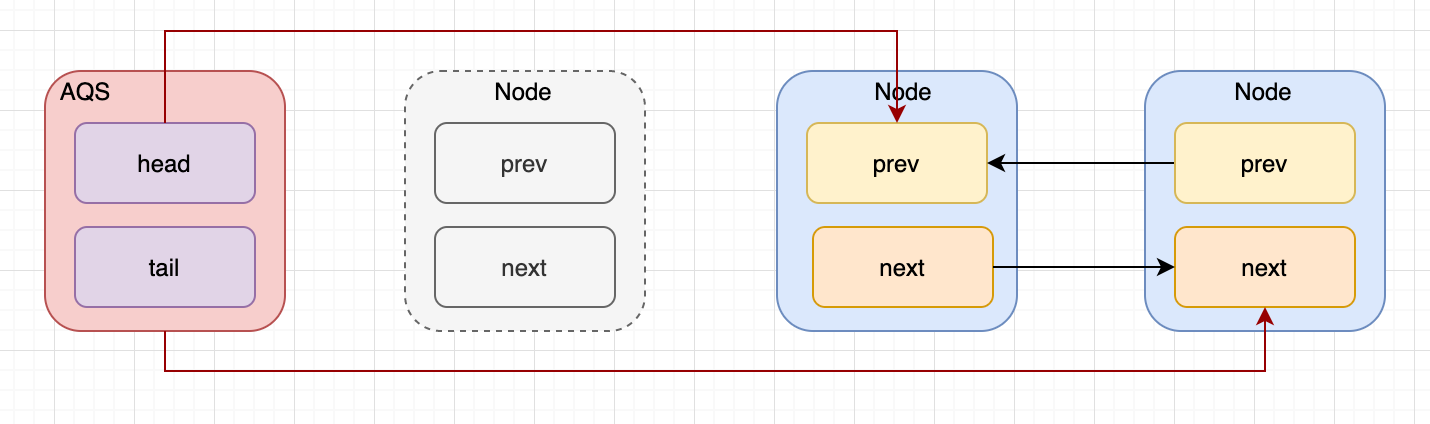
AQS-ReentrantLock
一、AQS 在 Lock 中,用到了一个同步队列 AQS,全称 AbstractQueuedSynchronizer,它是一个同步工具,也是 Lock 用来实现线程同步的核心组件。 1.AQS 的两种功能 独占和共享。 独占锁:每次只能有一个线程持有锁&#x…...

SpringCloud+Dubbo3 = 王炸 !
前言 全链路异步化的大趋势来了 随着业务的发展,微服务应用的流量越来越大,使用到的资源也越来越多。 在微服务架构下,大量的应用都是 SpringCloud 分布式架构,这种架构总体上是全链路同步模式。 全链路同步模式不仅造成了资源…...
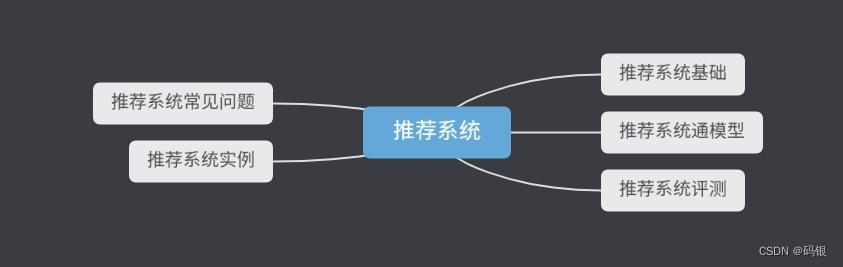
机器学习主要内容的思维导图
机器学习 机器学习: 定义:能够从经验中学习从而能够 把事情不断做好的计算机程序 人工智能的一个分支和 实现方式 理论基础:概率论 数理统计 线性代数 数学分析 数值逼近 最优化理论 计算复杂理论 核心要素:数据 算法 模型 机器…...

嵌套走马灯Carousel
Carousel 的应用很广泛,基础用法这里不多做阐述,感兴趣的可以去element-gui了解Carousel 组件。 今天主要是梳理嵌套走马灯的逻辑,背景如下: 需要对项目做一个展示,项目可能有一个或多个,同时一个项目可能…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...
