拓扑排序的思想?用代码怎么实现
目录
一、拓扑排序的思想
二、代码实现(C++)
代码思想
核心代码
完整代码
一、拓扑排序的思想
以西红柿炒鸡蛋这道菜为例,其中的做饭流程为: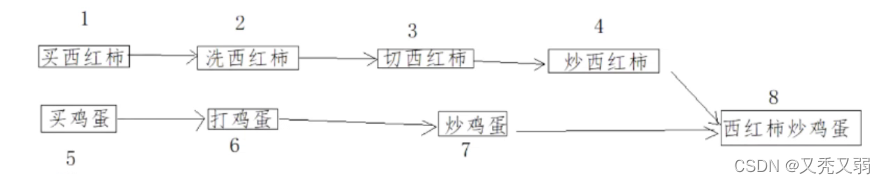
中间2 6 3 7 4的顺序都可以任意调换,但1和5必须在最前面,这是饭前准备,8必须在最后面。1和5的入度为0,出度为1,8的入度都2,出度为0
在这个操作流程内,把每个步骤当作一个顶点,排序连接起来就是个有向图。
排序,都是将元素按照一定的顺序/规则排列
拓扑排序就是将元素按照先后顺序进行排序
书面解释是:在一个表示工程的有向图中,用顶点表示活动,用弧表示活动之间的优先关系,这样的有向图为顶点表示活动的网,我们称为 AOV网(Activity On VertexNetwork)。AOV 网中的弧表示活动之间存在的某种制约关系。
特点是:有向无环(无回路)
拓扑序列:设G=(V,E)是一个具有 n个顶点的有向图V中的顶点序列 V1,V2····满足若从顶点到有一条路径,则在顶点序列中顶点必在顶点之前。则我们称这样的顶点序列为一个拓扑序列。
拓扑排序就是对一个有向图构造拓扑序列的过程。构造时会有两个结果,如果此网的全部顶点都被输出,则说明它是不存在环(回路)的AOV 网,如果输出顶点数少了,哪怕是少了一个,也说明这个网存在环(回路),不是AOV 网
拓扑排序的价值在于,不存在回路的AOV 网,我们可以将它应用在各种各样的工程或项目的流程图中,满足各种应用场景的需要。
二、代码实现(C++)
代码思想
从入度为0的顶点开始访问,访问完成后,将以此顶点为狐尾的弧删除(此顶点的邻接表中的顶点入度都减少1),然后继续查找剩余顶点中入度为0的顶点,重复操作,直到所有顶点都被访问完,或者没有了入度为0的顶点(说明此AOV有回路)
标记V1是从哪个顶点来的,借助栈来存储入度为0的顶点,栈的思想是先入后出
需要借助邻接表来存储图,邻接表内添加一个属性:顶点的入度,当创建图时,路径中每添加一条边时,就将入度+1,如果是v0->b1,则v1的度+1
先遍历度为0的节点,将其入栈,对栈顶元素在邻接表内查找其下一个顶点,并将下个顶点的度-1,设置为0。直到以该顶点所在的邻接表内的顶点的度都设置为0时,即代表将该顶点的狐尾删除。
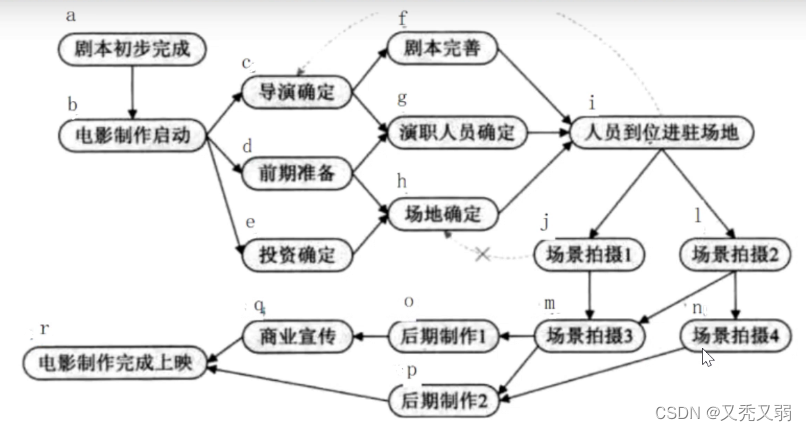
以该图为例,一张电影制作图,实现其中节点之间关联的排序
核心代码
int Graph::GetVertexIndex(char v)//获取顶点所在的下标
{int i;for (i = 0; i < m_NumVertex; i++){if (m_VerArr[i].m_value == v)return i;}return -1;
}
void Graph::InsertVertex(char v)//插入顶点
{if (m_NumVertex >= m_MaxVertex)return;m_VerArr[m_NumVertex++].m_value = v;
}void Graph::InsertEdge(char v1, char v2) //插入边
{int p1index = GetVertexIndex(v1);int p2index = GetVertexIndex(v2);if (p1index == -1 || p2index == -1)return;//v1-v2Edge* p = new Edge(p2index);p->m_next = m_VerArr[p1index].m_list;m_VerArr[p1index].m_list = p;m_VerArr[p2index].m_verIn++;
}
void Graph::TopologicalSort()//拓扑排序
{stack<int> ss;int i;Edge* p = NULL;for (i = 0; i < m_NumVertex; i++) //将入度为0的顶点入栈{if (m_VerArr[i].m_verIn == 0)ss.push(i);}for (i = 0; i < m_NumVertex; i++)//循环访问所有顶点进行拓扑排序
//该循环结束的条件:1.循环完,没有度为0的顶点再入栈即栈为空时,退出循环{if (ss.empty()){cout << "有回路" << endl;return;}else{int top = ss.top();//获取栈顶元素并出栈ss.pop();cout << m_VerArr[top].m_value << " ";//输出p = m_VerArr[top].m_list;//让P指向刚出来顶点的邻接表while (p)//循环遍历邻接表,设置入度-1{int in = --m_VerArr[p->m_destindex].m_verIn;//in为p所指向顶点的入度-1if (in == 0){ss.push(p->m_destindex);//入度为0时,说明顶点就是入读为0的顶点,对其下标入栈}p = p->m_next;}}}cout << endl;
}完整代码
#include<iostream>
using namespace std;
#define SIZE 20
class Edge //边
{
public:Edge() :m_next(NULL) {}Edge(int index) :m_destindex(index), m_next(NULL) {}int m_destindex;Edge* m_next;
};
class Vertex //顶点
{
public:Vertex() :m_list(NULL),m_verIn(0) {}Vertex(char v) :m_value(v), m_list(NULL),m_verIn(0) {}char m_value;Edge* m_list;int m_verIn;
};
class Graph
{
public:Graph();~Graph();void InsertVertex(char v);void InsertEdge(char v1, char v2);int GetVertexIndex(char v);void ShowGraph();void TopologicalSort();
private:int m_MaxVertex;int m_NumVertex;//Vertex* m_VerArr;Vertex m_VerArr[SIZE];
};#include<stack>
void Graph::TopologicalSort()//拓扑排序
{stack<int> ss;int i;Edge* p = NULL;for (i = 0; i < m_NumVertex; i++){if (m_VerArr[i].m_verIn == 0)ss.push(i);}for (i = 0; i < m_NumVertex; i++){if (ss.empty()){cout << "有回路" << endl;return;}else{int top = ss.top();ss.pop();cout << m_VerArr[top].m_value << " ";p = m_VerArr[top].m_list;while (p){int in = --m_VerArr[p->m_destindex].m_verIn;if (in == 0){ss.push(p->m_destindex);}p = p->m_next;}}}cout << endl;
}
void Graph::ShowGraph()
{Edge* p = NULL;for (int i = 0; i < m_NumVertex; i++){cout << i << " " <<m_VerArr[i].m_verIn<<" "<< m_VerArr[i].m_value << "->";p = m_VerArr[i].m_list;while (p != NULL){cout << p->m_destindex << "->";p = p->m_next;}cout << "nul" << endl;}
}
int Graph::GetVertexIndex(char v)
{int i;for (i = 0; i < m_NumVertex; i++){if (m_VerArr[i].m_value == v)return i;}return -1;
}
void Graph::InsertVertex(char v)
{if (m_NumVertex >= m_MaxVertex)return;m_VerArr[m_NumVertex++].m_value = v;
}
Graph::Graph()
{m_MaxVertex = SIZE;m_NumVertex = 0;//m_VerArr = new Vertex[m_MaxVertex];
}
Graph::~Graph()
{/* if (m_VerArr != NULL){delete[]m_VerArr;m_VerArr = NULL;}*/m_NumVertex = 0;
}
void Graph::InsertEdge(char v1, char v2)
{int p1index = GetVertexIndex(v1);int p2index = GetVertexIndex(v2);if (p1index == -1 || p2index == -1)return;//v1-v2Edge* p = new Edge(p2index);p->m_next = m_VerArr[p1index].m_list;m_VerArr[p1index].m_list = p;m_VerArr[p2index].m_verIn++;
}
void main()
{Graph g;//构建一个图g.InsertVertex('a');g.InsertVertex('b');g.InsertVertex('c');g.InsertVertex('d');g.InsertVertex('e');g.InsertVertex('f');g.InsertVertex('g');g.InsertVertex('h');g.InsertVertex('i');g.InsertVertex('j');g.InsertVertex('l');g.InsertVertex('m');g.InsertVertex('n');g.InsertVertex('o');g.InsertVertex('p');g.InsertVertex('q');g.InsertVertex('r');g.InsertEdge('a', 'b');g.InsertEdge('b', 'c');g.InsertEdge('b', 'd');g.InsertEdge('b', 'e');g.InsertEdge('c', 'f');g.InsertEdge('c', 'g');g.InsertEdge('d', 'g');g.InsertEdge('d', 'h');g.InsertEdge('e', 'h');g.InsertEdge('f', 'i');g.InsertEdge('g', 'i');g.InsertEdge('h', 'i');g.InsertEdge('i', 'j');g.InsertEdge('i', 'l');g.InsertEdge('j', 'm');g.InsertEdge('l', 'n');g.InsertEdge('l', 'm');g.InsertEdge('m', 'o');g.InsertEdge('m', 'p');g.InsertEdge('n', 'p');g.InsertEdge('o', 'q');g.InsertEdge('p', 'r');g.InsertEdge('q', 'r');g.ShowGraph();g.TopologicalSort();
}对各顶点和边的添加:第一列是顶点,第二列是计算所有顶点的入度情况,第三列是邻接表

相关文章:

拓扑排序的思想?用代码怎么实现
目录 一、拓扑排序的思想 二、代码实现(C) 代码思想 核心代码 完整代码 一、拓扑排序的思想 以西红柿炒鸡蛋这道菜为例,其中的做饭流程为: 中间2 6 3 7 4的顺序都可以任意调换,但1和5必须在最前面,这是…...
【Git】码云
目录 5、 Git 团队协作机制 5.1 团队内协作 5.2 跨团队协作 6、 Gitee码云 操作 6.1 创建远程仓库 6.2 远程仓库操作 6.3 SSH 免密登录 5、 Git 团队协作机制 5.1 团队内协作 5.2 跨团队协作 6、 Gitee码云 操作 码云网址: https://githee.com/ 账号验证…...
数据结构与算法(三):栈与队列
上一篇《数据结构与算法(二):线性表》中介绍了数据结构中线性表的两种不同实现——顺序表与链表。这一篇主要介绍线性表中比较特殊的两种数据结构——栈与队列。首先必须明确一点,栈和队列都是线性表,它们中的元素都具…...

Spring架构篇--2.5.2 远程通信基础Select 源码篇--window--sokcet.register
前言:通过Selector.open() 获取到Selector 的选择器后,服务端和客户的socket 都可以通过register 进行socker 的注册; 服务端 ServerSocketChannel 的注册: ServerSocketChannel serverSocketChannel ServerSocketChannel.open(…...
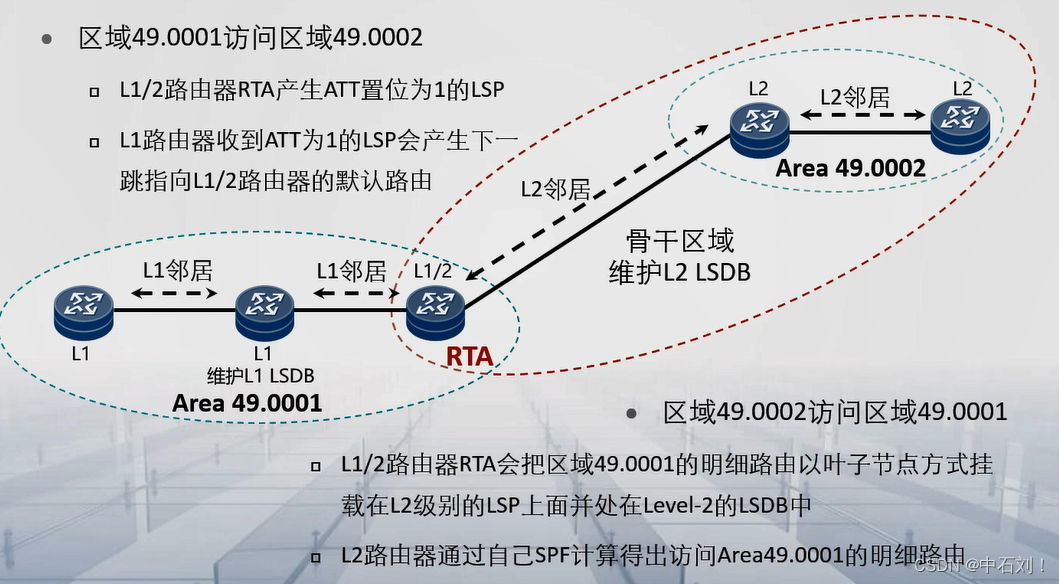
ISIS协议
ISIS协议基础简介应用场景路由计算过程地址结构路由器分类邻居Hello报文邻居关系建立DIS及DIS与DR的类比链路状态信息的载体链路状态信息的交互路由算法网络分层路由域区域间路由简介…...

CRM系统哪种品牌的好?这五款简单好用!
CRM系统哪种品牌的好?这五款简单好用! CRM系统是指利用软件、硬件和网络技术,为企业建立一个客户信息收集、管理、分析和利用的信息系统。CRM系统的基础功能主要包括营销自动化、客户管理、销售管理、客服管理、报表分析等,选择合…...
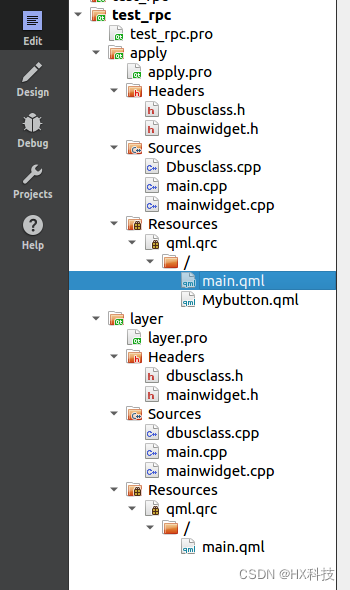
QT_dbus(ipc进程间通讯)
QT_dbus(ipc进程间通讯) 前言: 参考链接: https://www.cnblogs.com/brt3/p/9614899.html https://blog.csdn.net/weixin_43246170/article/details/120994311 https://blog.csdn.net/kchmmd/article/details/118605315 一个大型项目可能需要多个子程序同…...

华为OD机试 - 数组排序(C++) | 附带编码思路 【2023】
刷算法题之前必看 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD 清单查看地址:https://blog.csdn.net/hihell/category_12199283.html 华为OD详细说明:https://dream.blog.csdn.net/article/details/128980730 华为OD机试题…...
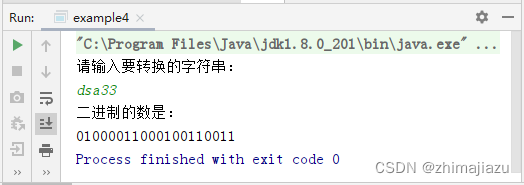
字符串转换为二进制-课后程序(JAVA基础案例教程-黑马程序员编著-第五章-课后作业)
【案例5-4】 字符串转换为二进制 【案例介绍】 1.任务描述 本例要求编写一个程序,从键盘录入一个字符串,将字符串转换为二进制数。在转换时,将字符串中的每个字符单独转换为一个二进制数,将所有二进制数连接起来进行输出。 案…...
SpringIOC
一、为什么要使用Spring? Spring 是个java企业级应用的开源开发框架。Spring主要用来开发Java应用,但是有些扩展是针对构建J2EE平台的web应用。Spring 框架目标是简化Java企业级应用开发,并通过POJO为基础的编程模型促进良好的编程习惯。 为…...

Debezium系列之:基于数据库信号表和Kafka信号Topic两种技术方案实现增量快照incremental技术的详细步骤
Debezium系列之:基于数据库信号表和Kafka信号Topic两种技术方案实现增量快照incremental技术的详细步骤 一、需求背景二、增量快照技术实现的两种方案三、基于数据库信号表实现增量快照技术的原理1.基于水印的快照2.信令表3.增量快照4.连接起重启四、基于数据库信号表实现增量…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 第 K 个最小码值的字母(Python) | 机试题+算法思路+考点+代码解析 【2023】
第 K 个最小码值的字母 题目 输入一个由n个大小写字母组成的字符串 按照 ASCII 码值从小到大进行排序 查找字符串中第k个最小 ASCII 码值的字母(k>=1) 输出该字母所在字符串中的位置索引(字符串的第一个位置索引为 0) k如果大于字符串长度则输出最大 ASCII 码值的字母所在…...
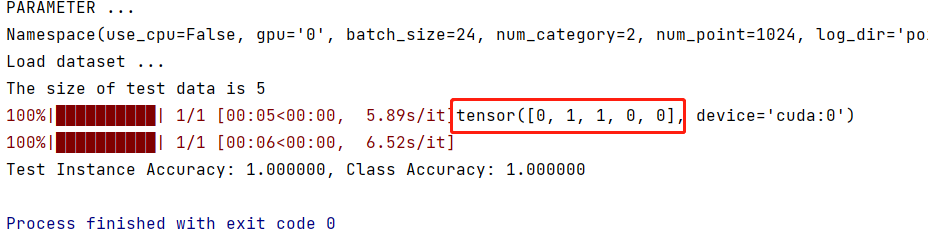
PointNet++训练自己的数据集(附源码)
本文针对PointNet强大的三维点云分类功能,详细讲解怎么训练自己的数据集,在此之前,需要确保已经能够跑通源码的训练和测试,如果没有,请参考PointNet的源码运行。数据放置1.1. 在mytensor_shape_names.txt中配置自己的分…...
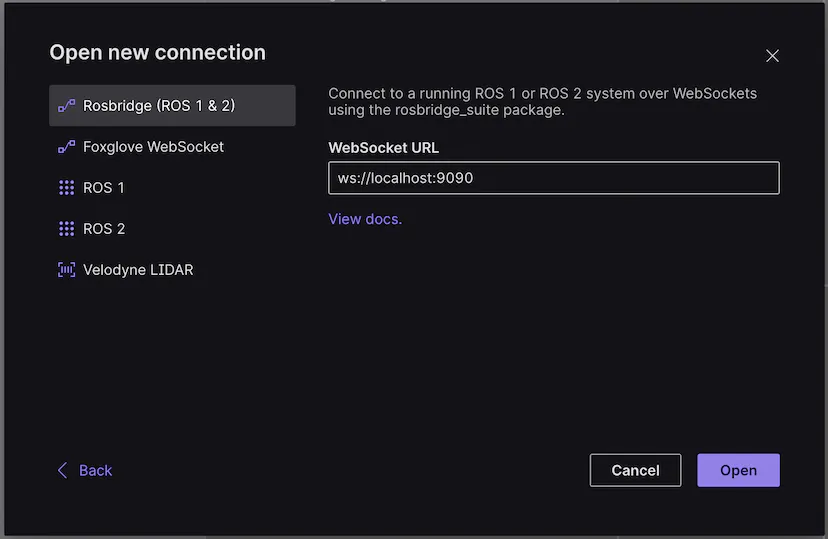
ROS2可视化利器---Foxglove Studio
0. 简介 之前作者已经讲了《ROS1可视化利器—Webviz》,然后就有读者问,ROS2有没有可以使用的可视化工具呢,答案是肯定的,除了plotjuggler这种ROS1和ROS2通用的可视化利器,还有一种全平台通用的软件FoxgloveStudio&…...
)
python实战应用讲解-【语法基础篇】流程控制-控制流的元素及语句(附示例代码)
目录 控制流的元素 条件 代码块 程序执行 代码块嵌套 控制流语句 if 语句...

[蓝桥杯 2019 省 A] 外卖店优先级
蓝桥杯 2019 年省赛 A 组 G 题题目描述“饱了么”外卖系统中维护着 N家外卖店,编号 1 ∼ N。每家外卖店都有一个优先级,初始时 (0 时刻)优先级都为0。每经过 1 个时间单位,如果外卖店没有订单,则优先级会减少 1&#x…...
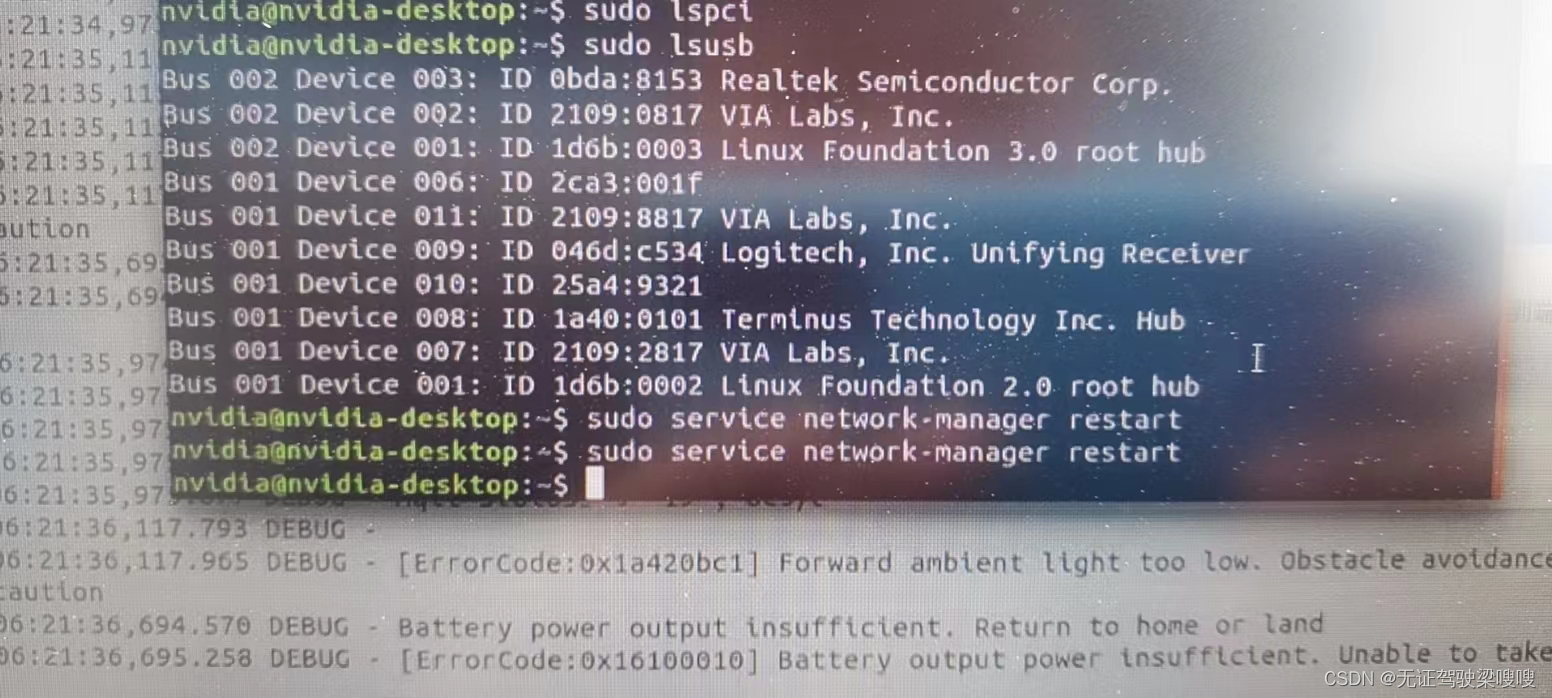
Jetson Xavier nx(ubuntu18.04)安装rtl8152网卡驱动和8192网卡驱动
含义 Bus 002 : 指明设备连接到哪条总线。 Device 003 : 表明这是连接到总线上的第二台设备。 ID : 设备的ID,包括厂商的ID和产品的ID,格式 厂商ID:产品ID。 Realtek Semiconductor Corp. RTL8153 Gigabit Ethernet Adapter:生产商名字和设备…...

Rocky 9.1操作系统实现zabbix6.0的安装部署实战
文章目录前言一. 实验环境二. 安装zabbix过程2.1. 安装zabbix源2.2 安装zabbix相关的软件2.3 安装数据库并启动2.4 开始初始化数据库:2.5 创建数据库实例及对应的用户2.6 导入官网提供的数据2.7 配置zabbix 服务的配置文件2.8. 启动服务2.9 从网页进行安装2.10 登陆…...
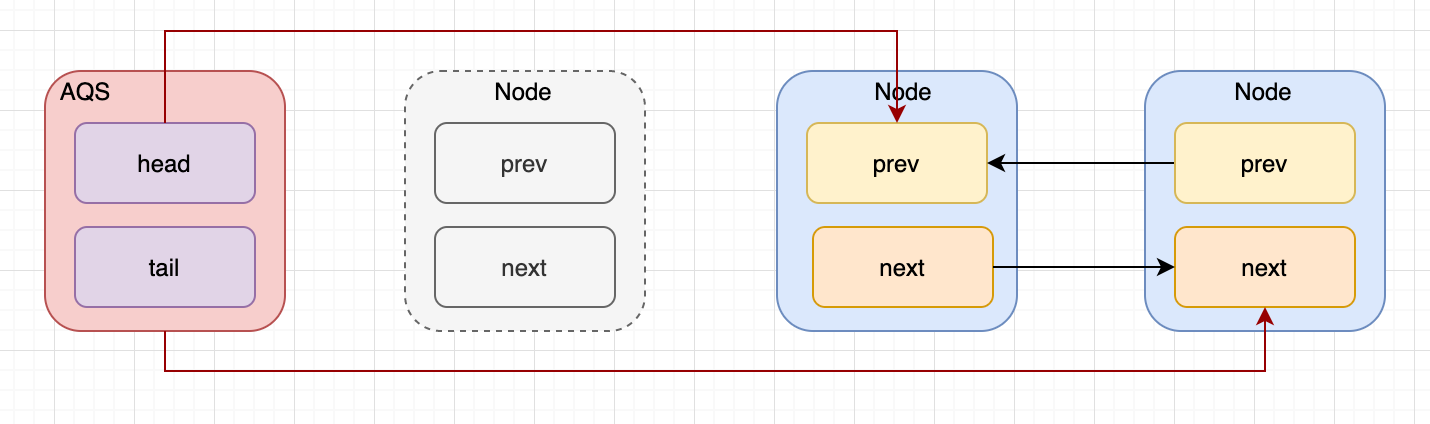
AQS-ReentrantLock
一、AQS 在 Lock 中,用到了一个同步队列 AQS,全称 AbstractQueuedSynchronizer,它是一个同步工具,也是 Lock 用来实现线程同步的核心组件。 1.AQS 的两种功能 独占和共享。 独占锁:每次只能有一个线程持有锁&#x…...

SpringCloud+Dubbo3 = 王炸 !
前言 全链路异步化的大趋势来了 随着业务的发展,微服务应用的流量越来越大,使用到的资源也越来越多。 在微服务架构下,大量的应用都是 SpringCloud 分布式架构,这种架构总体上是全链路同步模式。 全链路同步模式不仅造成了资源…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...

C# WPF 左右布局实现学习笔记(1)
开发流程视频: https://www.youtube.com/watch?vCkHyDYeImjY&ab_channelC%23DesignPro Git源码: GitHub - CSharpDesignPro/Page-Navigation-using-MVVM: WPF - Page Navigation using MVVM 1. 新建工程 新建WPF应用(.NET Framework) 2.…...

标注工具核心架构分析——主窗口的图像显示
🏗️ 标注工具核心架构分析 📋 系统概述 主要有两个核心类,采用经典的 Scene-View 架构模式: 🎯 核心类结构 1. AnnotationScene (QGraphicsScene子类) 主要负责标注场景的管理和交互 🔧 关键函数&…...
