数据在内存中的存储【下篇】
文章目录
- ⚙️3.浮点型在内存中的存储
- 🔩3.1.一个例子
- 🔩3.2.浮点数的存储规则
- 🔩3.3.例题解析

⚙️3.浮点型在内存中的存储
🔩3.1.一个例子
🔴浮点数存储的例子:👇
int main()
{int n = 9;float* pFloat = (float*)&n;printf("n的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);*pFloat = 9.0;printf("num的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);return 0;
}
🥰可以先猜想一下打印的4个值分别是多少?

📀整型和浮点型在内存的存储是有区别的
🔩3.2.浮点数的存储规则
💡根据国际标准IEEE(电气和电子工程协会)754,任意一个二进制浮点数V可以表示成下面的形式:
🔴 (-1)^S * M * 2^E
🔴 (-1)^S 表示符号位,当S=0,V为正数;当S=1,V为负数
🔴 M 表示有效数字,大于等于1,小于2
🔴 2^E 表示指数位
💡我们举个栗子:
假如一个10进制浮点数为5.5,我们应该怎么转换成上面的形式呢?

二进制的数据的每一位权重是这样分布的☝️

根据规则,转换完之后就是这样的☝️
IEEE 754规定:
对于32位的浮点数(float),最高的一位是符号位S,接着的8位是指数E,剩下的23位为有效数字M

对于64位的浮点数(double),最高的一位是符号位S,接着的11位是指数E,剩下的52位为有效数字M

🔴IEEE 754对有效数字M和指数E,还有一些特别规定:
前面说过,1<=M<2,也就是说,M可以写成 1.xxxxxx 的形式,其中 xxxxxx 表示小数部分
IEEE 754规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的 xxxxxx部分,比如保存 1.01的时候,只保存01,等到读取的时候,再把第一位的1加上去,这样做的目的,是节省1位有效数字,以32位浮点数为例,留给M只有23位,将第一位的1舍去以后,等于可以保存24位有效数字
🔴至于指数E,情况就比较复杂:
首先E为一个无符号整数(unsigned int)这意味着,如果E为8位,它的取值范围为0 ~ 255;如果E为11位,它的取值范围为0 ~ 2047。但是,我们知道,科学计数法中的E是可以出现负数的(比如0.5 = 1.0 * 2^-1),所以IEEE 754规定,存入内存时E的真实值必须再加上一个中间数,对于8位的E,这个中间数是127;对于11位的E,这个中间数是1023。比如,2 ^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001
💡举个栗子:5.5
int main()
{float f = 5.5f;// 101.1// (-1)^0 * 1.011 * 2^2// 0 10000001 011 00000000000000000000// S E(2+127) M 补20个0(补齐23位)// 40b00000 --- 16进制return 0;
}
可以调试看一下内存👇
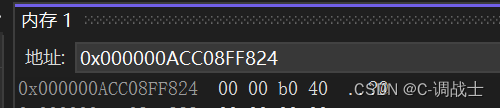
🥰根据规则,由此就可以知道了浮点数是如何存储的了
🔴指数E从内存中取出还可以再分成三种情况:
🔔E不全为0或不全为1
这时,浮点数就采用下面的规则表示,即指数E的计算值减去127(或1023),得到真实值,再将有效数字M前加上第一位1
比如:
0.5(1/2)的二进制形式为0.1,由于规定正数部分必须为1,即将小数点右移1位,则为1.0*2^(-1),其阶码为 -1+127=126,表示为 01111110,而尾数1.0去掉整数部分为0,补齐0到23位00000000000000000000000,则其二进制表示形式为:0 01111110 00000000000000000000000
🔔E全为0
这时,浮点数的指数E等于1-127(或者1-1023)即为真实值
有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数。这样做是为了表示±0,以及接近于0的很小的数字
🔔E全为1
这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位S)
🔩3.3.例题解析
int main()
{int n = 9;//00000000000000000000000000001001 -- 9的补码//0 00000000 00000000000000000001001//E = 1-127 = -126//M = 0.00000000000000000001001//(-1)^0 * 0.00000000000000000001001 * 2^-126float* pFloat = (float*)&n;printf("n的值为:%d\n", n);//9printf("*pFloat的值为:%f\n", *pFloat);//0.0*pFloat = 9.0;//以浮点数的视角,存放浮点型的数字//1001.0//1.001 * 2^3//(-1)^0 * 1.001 * 2^3//S = 0//E = 3//M = 1.001//0 (3+127)10000010 00100000000000000000000 -- 补码=原码printf("num的值为:%d\n", n);//1091567616printf("*pFloat的值为:%f\n", *pFloat);//9.0return 0;
}
☝️double类型原理也是如此☝️
🥰希望大家可以理解🥰
总结🥰
以上就是 数据在内存中的存储下篇 内容啦🥳🥳🥳🥳
本文章所在【C语言知识篇】专栏,感兴趣的烙铁可以订阅本专栏哦🥳🥳🥳
希望我们可以做一个用心的人💕💕💕
小的会继续学习,继续努力带来更好的作品😊😊😊
创作写文不易,还多请各位大佬uu们多多支持哦🥰🥰🥰
相关文章:

数据在内存中的存储【下篇】
文章目录⚙️3.浮点型在内存中的存储🔩3.1.一个例子🔩3.2.浮点数的存储规则🔩3.3.例题解析⚙️3.浮点型在内存中的存储 🔩3.1.一个例子 🔴浮点数存储的例子:👇 int main() {int n 9;float* …...

前端开发项目规范写法介绍
1. 基本原则 结构、样式、行为分离 尽量确保文档和模板只包含 HTML 结构,样式都放到样式表里,行为都放到脚本里。 缩进 统一两个空格缩进(总之缩进统一即可),不要使用 Tab 或者 Tab、空格混搭。 文件编码 使用不带 BOM 的 UTF-8 编码。 在 HTML中指定编码 <meta c…...

百万医疗险是什么
一、百万医疗险是什么 从名字可以看出,这是一款医疗险。因为保额高,最高能报销百万,所以叫百万医疗险。 二、百万医疗险有什么用 可以报销被保险人因意外伤害和疾病导致的医疗费用 三、如何挑选 虽然高达几百万的保额,但保额却并非…...

矩阵中的路径 AcWing (JAVA)
请设计一个函数,用来判断在一个矩阵中是否存在一条路径包含的字符按访问顺序连在一起恰好为给定字符串。 路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。 如果一条路径经过…...

使用终端工具给你的电脑发送弹窗提醒
大家好,我是良许。 现在人手一部智能手机,这些智能手机都有个非常实用的功能,那就是弹窗提醒。当我们收到短信,或者微信信息时,手机就会弹窗显示信息的大致内容。有了这个功能你就不会错过重要信息了。 电脑上也有类…...
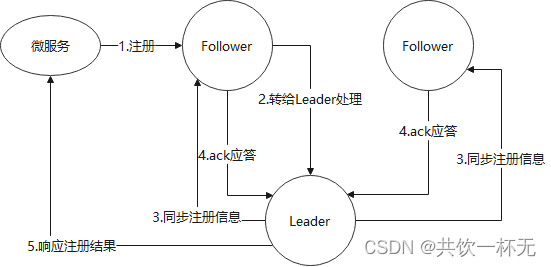
SpringCloud Alibaba 之Nacos集群部署-高可用保证
文章目录Nacos集群部署Linux部署docker部署(参考待验证)Nacos 集群的工作原理Nacos 集群中 Leader 节点是如何产生的Nacos 节点间的数据同步过程官方推荐用户把所有服务列表放到一个vip下面,然后挂到一个域名下面。http://nacos.com:port/ope…...
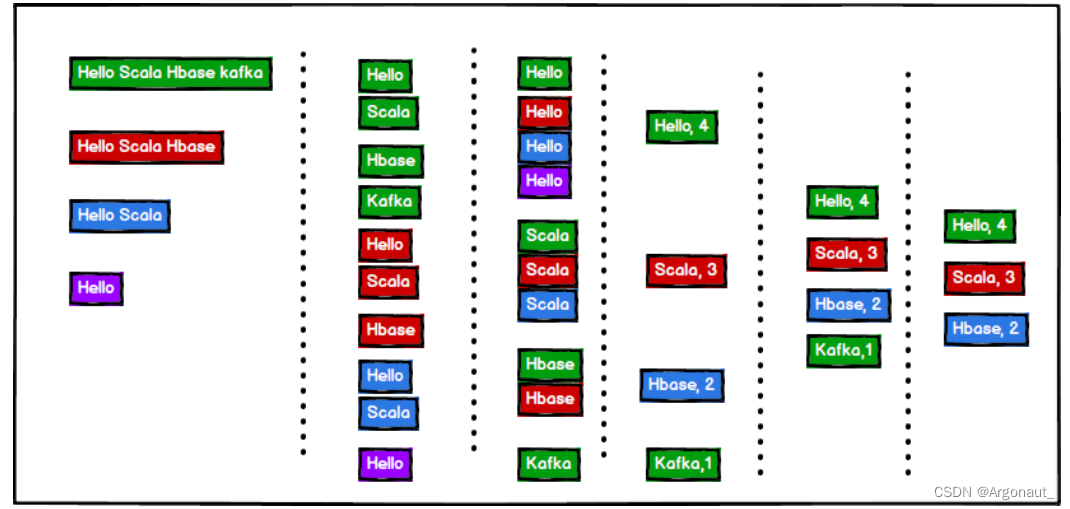
Scala集合详解(第七章:集合、数组、列表、set集合、map集合、元组、队列、并行)(尚硅谷笔记)
集合第七章:集合7.1 集合简介7.1.1 不可变集合继承图7.1.2 可变集合继承图7.2 数组7.2.1 不可变数组7.2.2 可变数组7.2.3 不可变数组与可变数组的转换7.2.4 多维数组7.3 列表 List7.3.1 不可变 List7.3.2 可变 ListBuffer7.4 Set 集合7.4.1 不可变 Set7.4.2 可变 mutable.Set7.…...
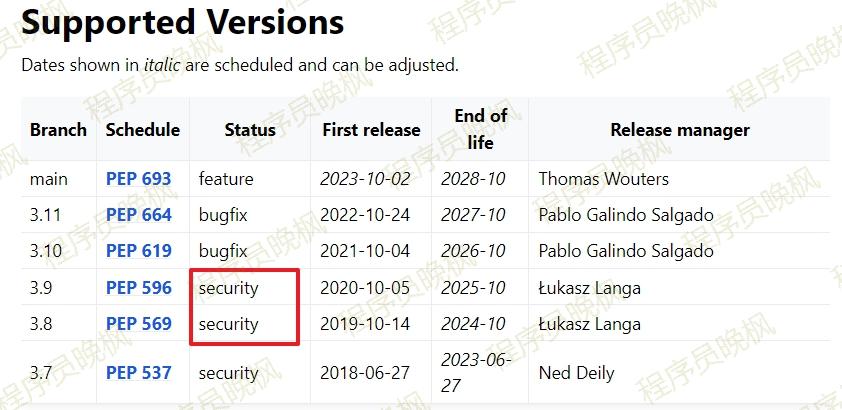
定了:Python3.7,今年停止更新~
大家好,这里是程序员晚枫。 今天给大家分享一个来自Python官网的重要消息:Python3.7马上就要停止维护了,请不要使用了! 官网链接:https://devguide.python.org/versions/ 停更的后果是什么? 周末翻阅Py…...
C# 业务单据号生成器(定义规则、获取编号、流水号)
系列文章 C#底层库–数据库访问帮助类(MySQL版) 本文链接:https://blog.csdn.net/youcheng_ge/article/details/126886379 C#底层库–JSON帮助类_详细(序列化、反序列化、list、datatable) 本文链接:htt…...
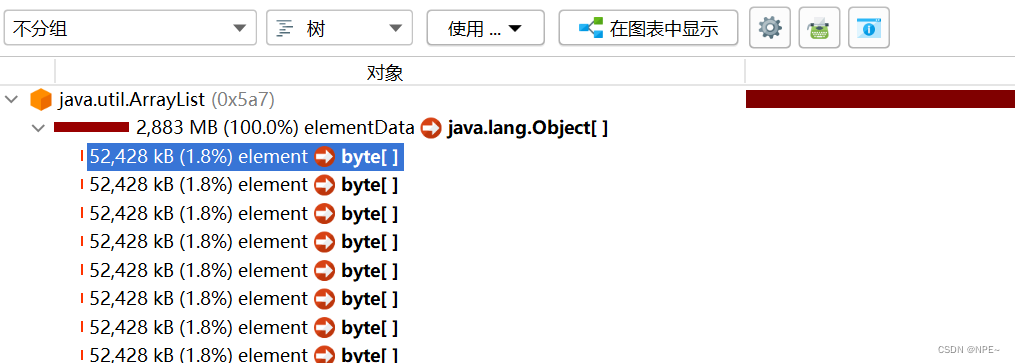
Java的dump文件分析及JProfiler使用
Java的dump文件分析及JProfiler使用 1 dump文件介绍 从软件开发的角度上,dump文件就是当程序产生异常时,用来记录当时的程序状态信息(例如堆栈的状态),用于程序开发定位问题。 idea配置发生OOM的时候指定路径生成dump文件 # 指定…...
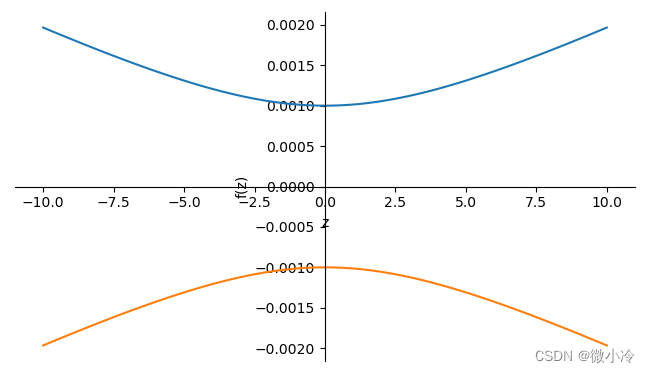
sympy高斯光束模型
文章目录Gauss模型sympy封装实战sympy.phisics.optics.gaussopt集成了高斯光学中的常见对象,包括光线和光学元件等,有了这些东西,就可以制作一个光学仿真系统。Gauss模型 高斯光束的基本模型为 E(r,z)E0ω0ω(z)exp[−r2ω2(z)]exp[−ik…...
Cloudflared 内网穿透 使用记录
Cloudflared 内网穿透前提创建cloudflared tunnel我使用的服务前提 你必须要有一个域名,并且可以改域名的dns解析服务商到cloudflare 1.登录到cloudflare后台,点击添加站点 2.输入自己的域名,下一步选择免费套餐 3.他会搜索这个域名下已有…...

柴油发电机组的调压板
1 概述 柴油发电机组的调压板是一种用于控制发电机输出电压的装置。它通常由一块电子电路板和一个电子电路板上的电位器组成。 当发电机运行时,它会产生电压,然后通过调压板中的电路进行控制。调压板中的电路会检测输出电压的大小,并通过电…...

【MySQL】表操作和库操作
文章目录概念库操作1.创建数据库2.删除数据库3.选择数据库4.显示数据库列表表操作1.创建数据表CREATE2.删除数据表DROP3.插入数据INSERT4.更新数据UPDATE5.修改数据ALTER6.查询数据SELECT7.WHERE子句8.ORDER BY子句9.LIMIT子句10.GROUP BY子句11.HAVING子句使用注意事项概念 M…...

拓扑排序的思想?用代码怎么实现
目录 一、拓扑排序的思想 二、代码实现(C) 代码思想 核心代码 完整代码 一、拓扑排序的思想 以西红柿炒鸡蛋这道菜为例,其中的做饭流程为: 中间2 6 3 7 4的顺序都可以任意调换,但1和5必须在最前面,这是…...
【Git】码云
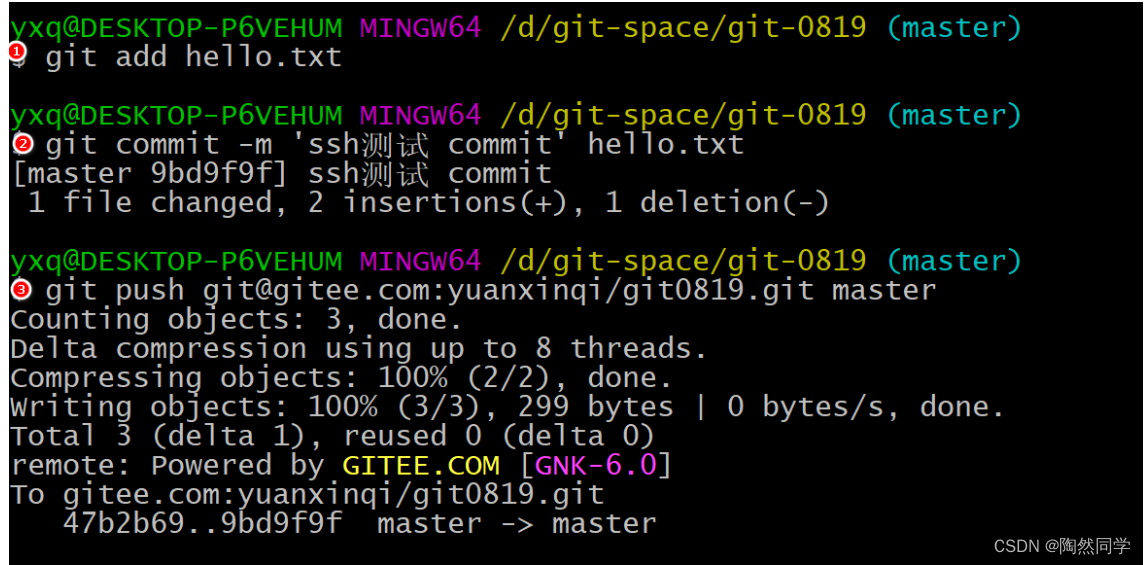
目录 5、 Git 团队协作机制 5.1 团队内协作 5.2 跨团队协作 6、 Gitee码云 操作 6.1 创建远程仓库 6.2 远程仓库操作 6.3 SSH 免密登录 5、 Git 团队协作机制 5.1 团队内协作 5.2 跨团队协作 6、 Gitee码云 操作 码云网址: https://githee.com/ 账号验证…...
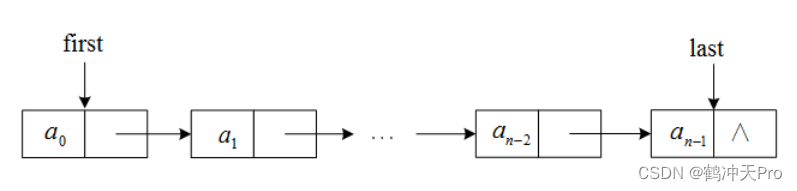
数据结构与算法(三):栈与队列
上一篇《数据结构与算法(二):线性表》中介绍了数据结构中线性表的两种不同实现——顺序表与链表。这一篇主要介绍线性表中比较特殊的两种数据结构——栈与队列。首先必须明确一点,栈和队列都是线性表,它们中的元素都具…...

Spring架构篇--2.5.2 远程通信基础Select 源码篇--window--sokcet.register
前言:通过Selector.open() 获取到Selector 的选择器后,服务端和客户的socket 都可以通过register 进行socker 的注册; 服务端 ServerSocketChannel 的注册: ServerSocketChannel serverSocketChannel ServerSocketChannel.open(…...
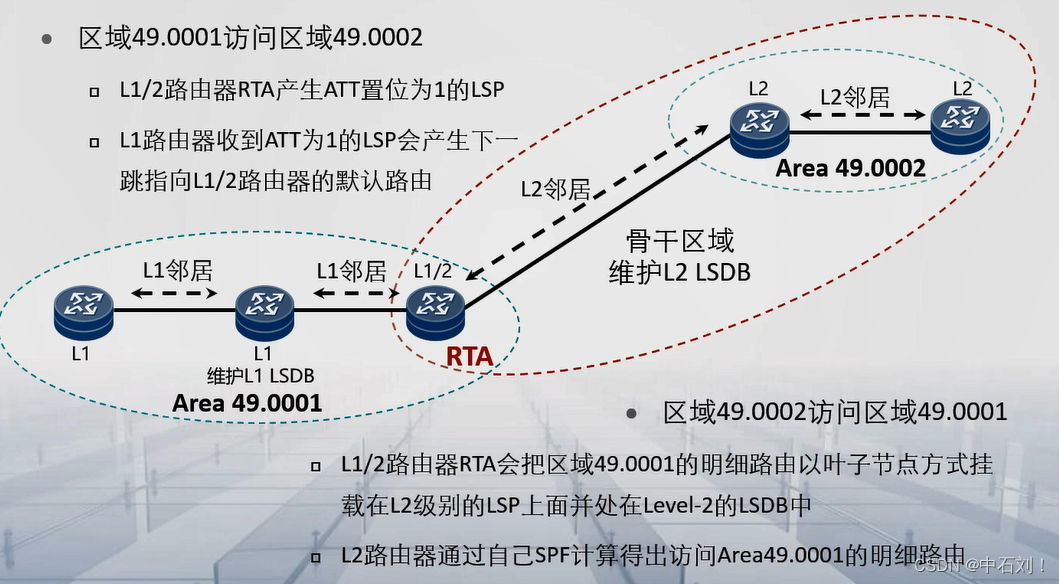
ISIS协议
ISIS协议基础简介应用场景路由计算过程地址结构路由器分类邻居Hello报文邻居关系建立DIS及DIS与DR的类比链路状态信息的载体链路状态信息的交互路由算法网络分层路由域区域间路由简介…...

CRM系统哪种品牌的好?这五款简单好用!
CRM系统哪种品牌的好?这五款简单好用! CRM系统是指利用软件、硬件和网络技术,为企业建立一个客户信息收集、管理、分析和利用的信息系统。CRM系统的基础功能主要包括营销自动化、客户管理、销售管理、客服管理、报表分析等,选择合…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...
