【算法基础】一维前缀和 + 二维前缀和

👦个人主页:Weraphael
✍🏻作者简介:目前正在学习c++和算法
✈️专栏:【C/C++】算法
🐋 希望大家多多支持,咱一起进步!😁
如果文章有啥瑕疵
希望大佬指点一二
如果文章对你有帮助的话
欢迎 评论💬 点赞👍🏻 收藏 📂 加关注😍
目录
- 一、一维前缀和
- 1.1 什么是一维前缀和
- 1.2 如何求Sn
- 1.3 用途
- 1.4 代码模板
- 1.5 细节问题
- 二、二维前缀和
- 2.1 用途
- 2.2 前缀和S[i][j]求法
- 2.3 子矩阵求法
- 2.4 代码模板
- 三、总结
一、一维前缀和
1.1 什么是一维前缀和
前缀和就是新建一个数组,数组中保存的是原数组前
n项的和
【举个例子】
- Sn = a1+a2+a3+…an, Sn就是数列的前缀和(下标一定要从1开始,后面会讲解原因)
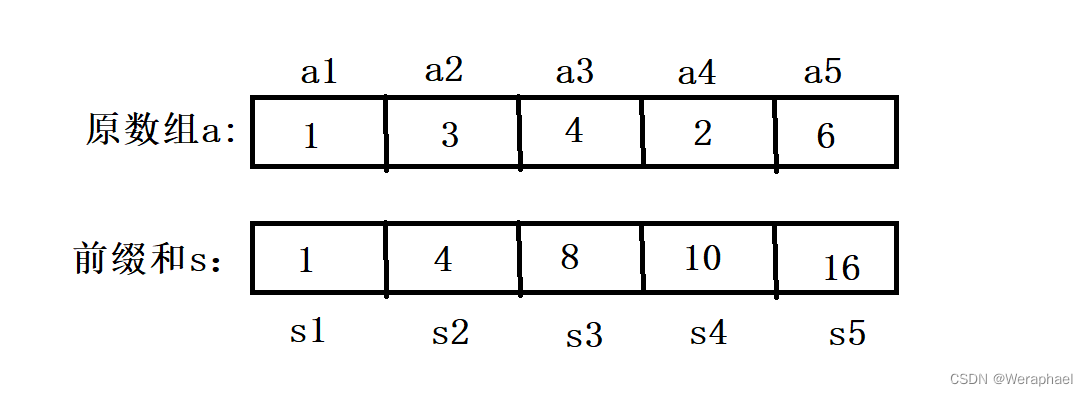
1.2 如何求Sn
我们可以利用上面的图来找找规律
- S1 = a1
- S2 = a1 + a2 = S1 + a2
- S3 = a1 + a2 + a3 = S2 + a3
- S4 = a1 + a2 + a3 + a4 = S3 + a4
- S5 = a1 + a2 + a3 + a4 + a5 = S4 + a5
- 这一套下来,前缀和的公式很明显就是:Si = Si-1 + ai
【代码】
for (int i = 1;i <= n;i++)
{s[i] = s[i-1] + a[i];
}
1.3 用途
能快速求出数列中某一段的和,时间复杂度为O(1)
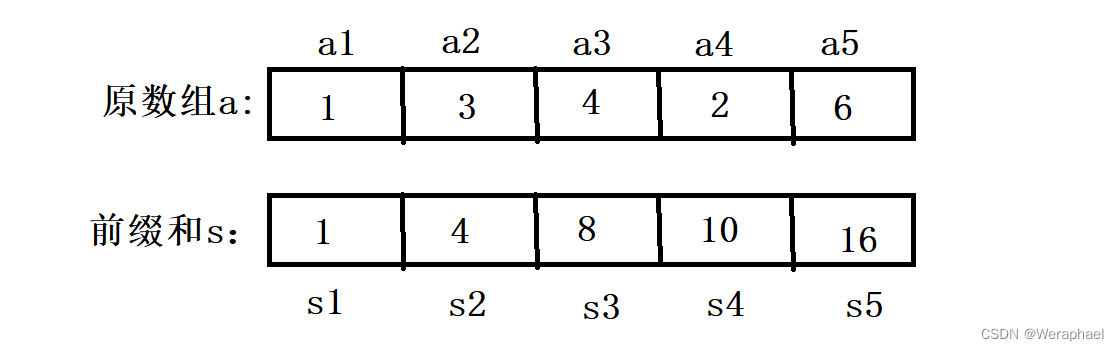
还是要利用这幅图
假设我们要计算原数组a中区间[2,4]的和,我们就可以用S4 - S1,

- 总结:假设日后题目要求区间[
l,r]的和,其实也能循环遍历,不过时间复杂度是O(N),而前缀和的时间复杂度是O(1) - 计算区间[l,r]的和,其公式为Sr - Sl-1
1.4 代码模板
#include <iostream>
using namespace std;const int N = 100010;
int a[N],s[n];int main()
{int n; //n - 原数组元素的个数scanf("%d",&n);//输入原数组for (int i = 1;i <= n;i++) {scanf("%d",&a[i]);}//前缀和公式for (int i = 1;i <= n;i++){s[i] = s[i - 1] + a[i];}//以下是计算某段区间的和int l,r;scanf("%d%d",&l,&r);printf("%d\n",s[r] - s[l - 1]);return 0;
}
1.5 细节问题
- 首先,下标从1开始就是为了定义S0,就拿前缀和公式来说,
S[i] = S[i-1] + a[i],当i = 1时,出现了S0,而S0要及时置为0,原因是为了统一。举个例子,假设要计算区间[1,10]之间的和,明眼就能看出是要计算S10,而为了达到统一计算的效果,S10 - S0 = S10 - 0.- 为什么我在代码中没有定义
S[0]=0,原因是我将s[N]定成了全局变量,而全局变量有一个特点:默认初始化为0!
二、二维前缀和
2.1 用途
目的是求出一个矩阵中某一个小矩阵的和
2.2 前缀和S[i][j]求法
大家画图可能会更加容易理解点,假设点(i,j)在矩阵的正中心,S[i][j] 即为黄色部分所有数的的和
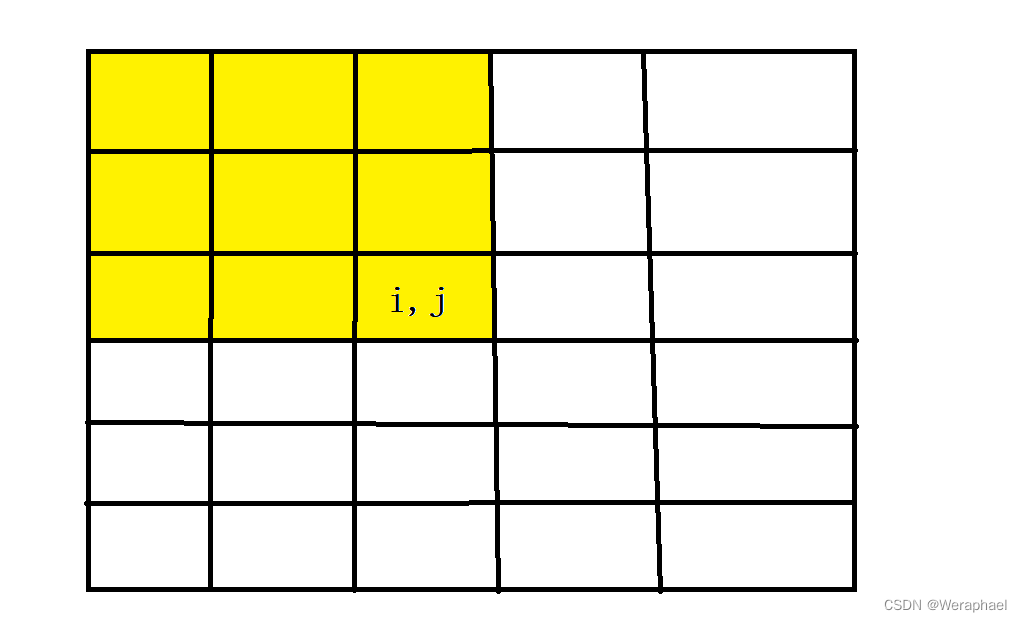
我们可以分三步求出黄色部分的和
- 第一步先求出红色部分所有数的和
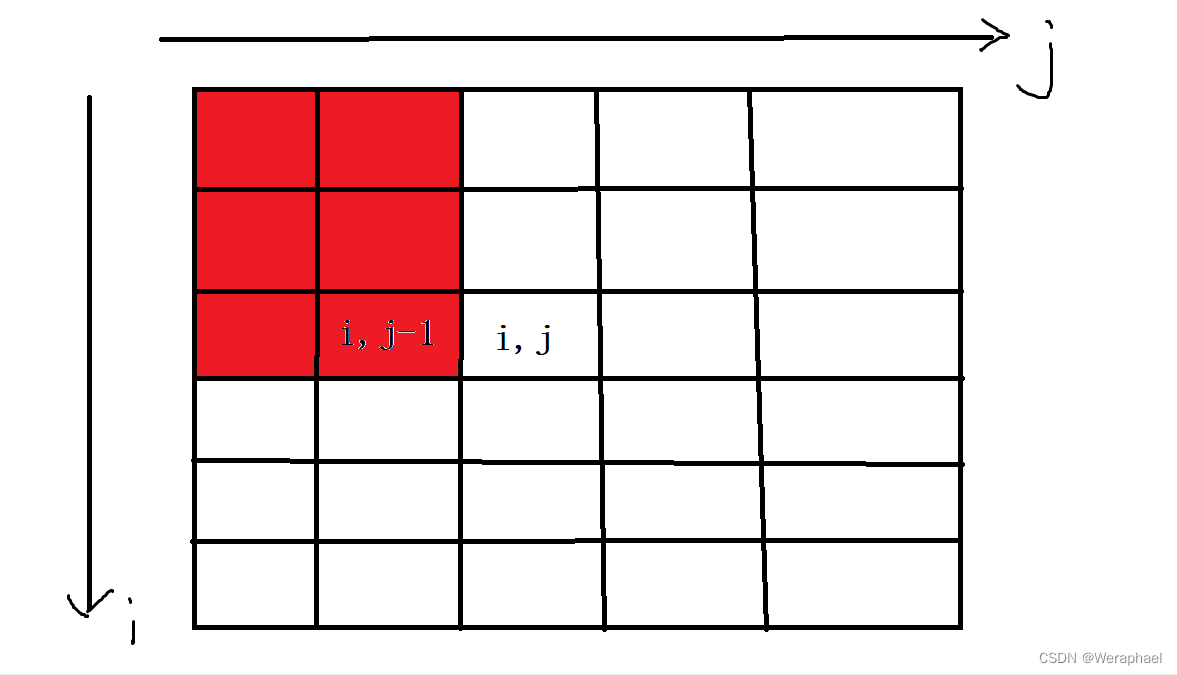
列出式子:
S[i][j] = S[i][j-1] + ...
- 第二步再求出绿色部分所有数的和
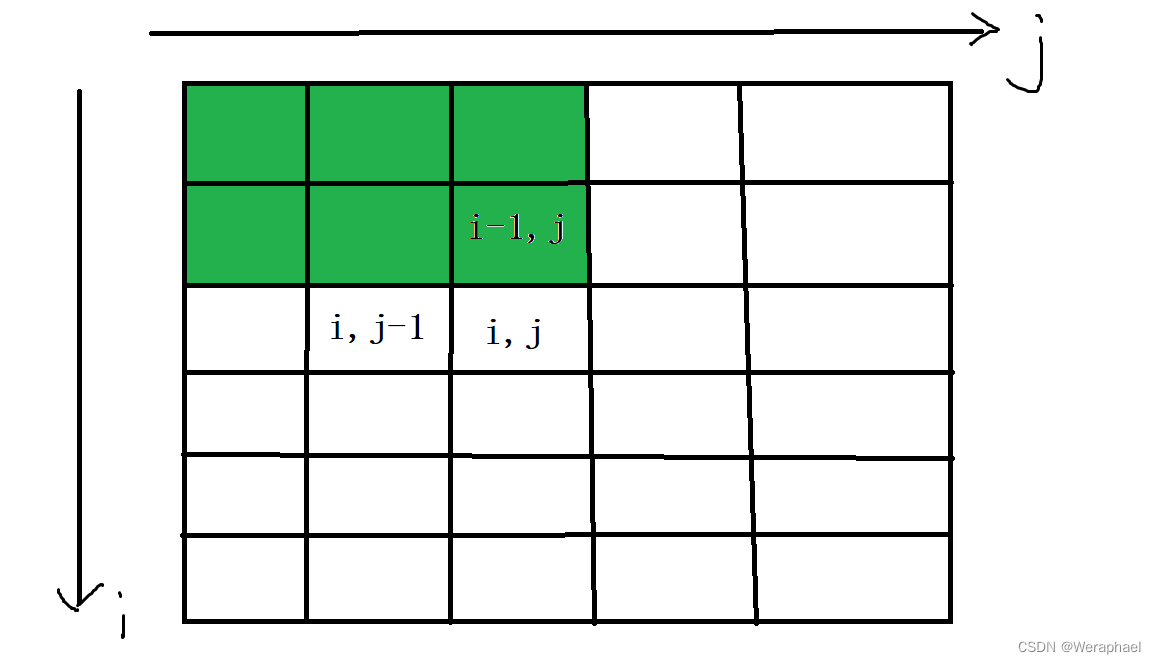
列出式子:
S[i][j] = S[i][j-1] + S[i-1][j] + ...
- 第三步去重,因为前两部重复加上了黑色部分所有数的和,因此要减掉一次
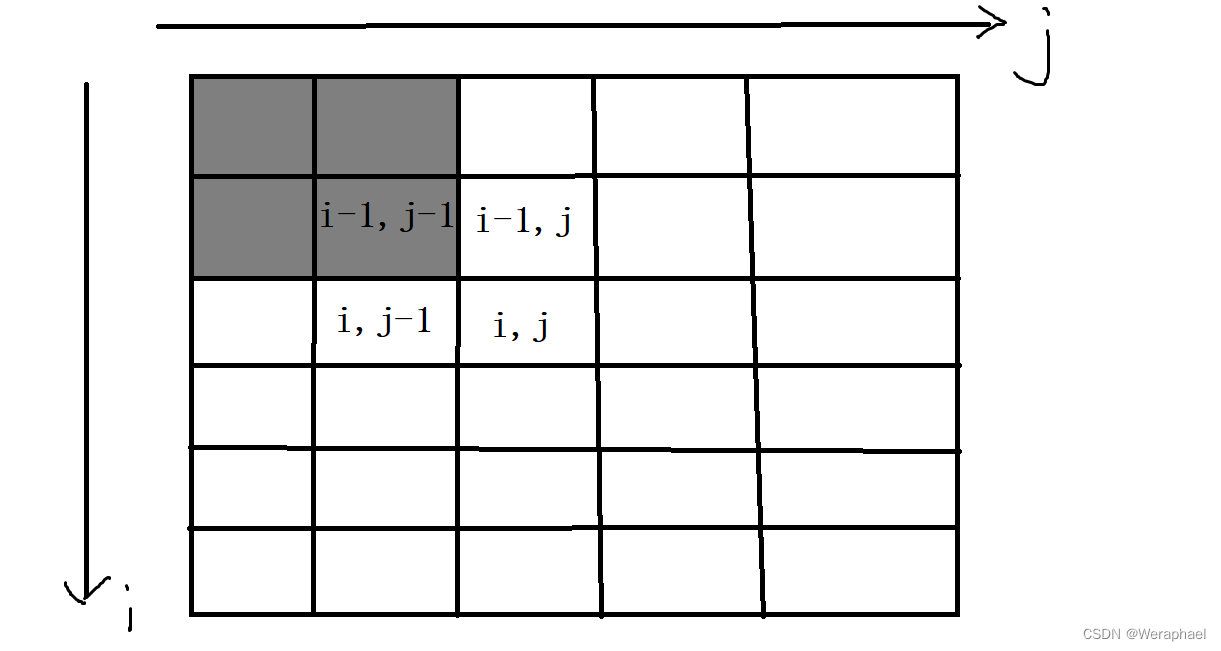
最后别忘了加上了本身:
a[i][j]
列出式子:S[i][j] = S[i][j-1] + S[i-1][j] - S[i-1][j-1] + a[i][j]
2.3 子矩阵求法
假设要求左上角为(x1,y1),右下角为(x2,y2)所围成黄色部分所有数的和
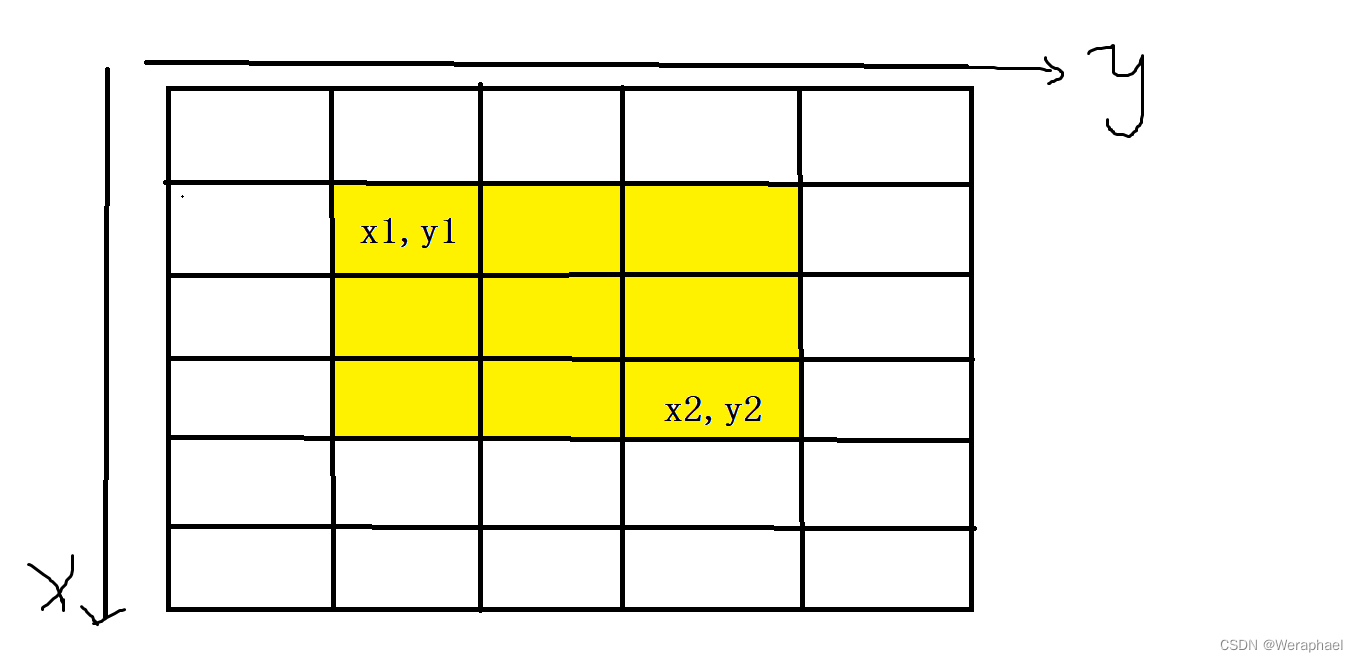
子矩阵的求法和求S[i][j]是类似的,四步走
- 第一步,先求出红色部分围成所有数的和
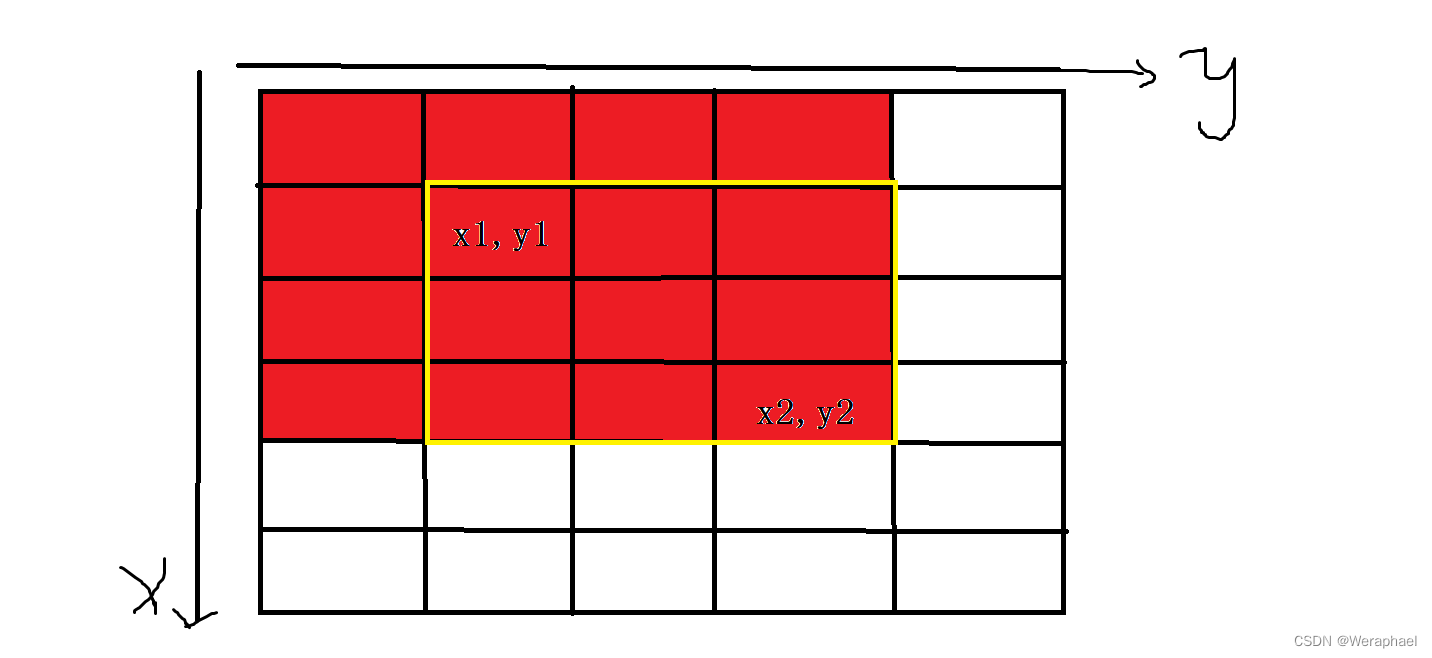
列出式子:
S = S[x2][y2] - ...
- 第二步,在用上一步红色部分减去绿色部分所有数的和
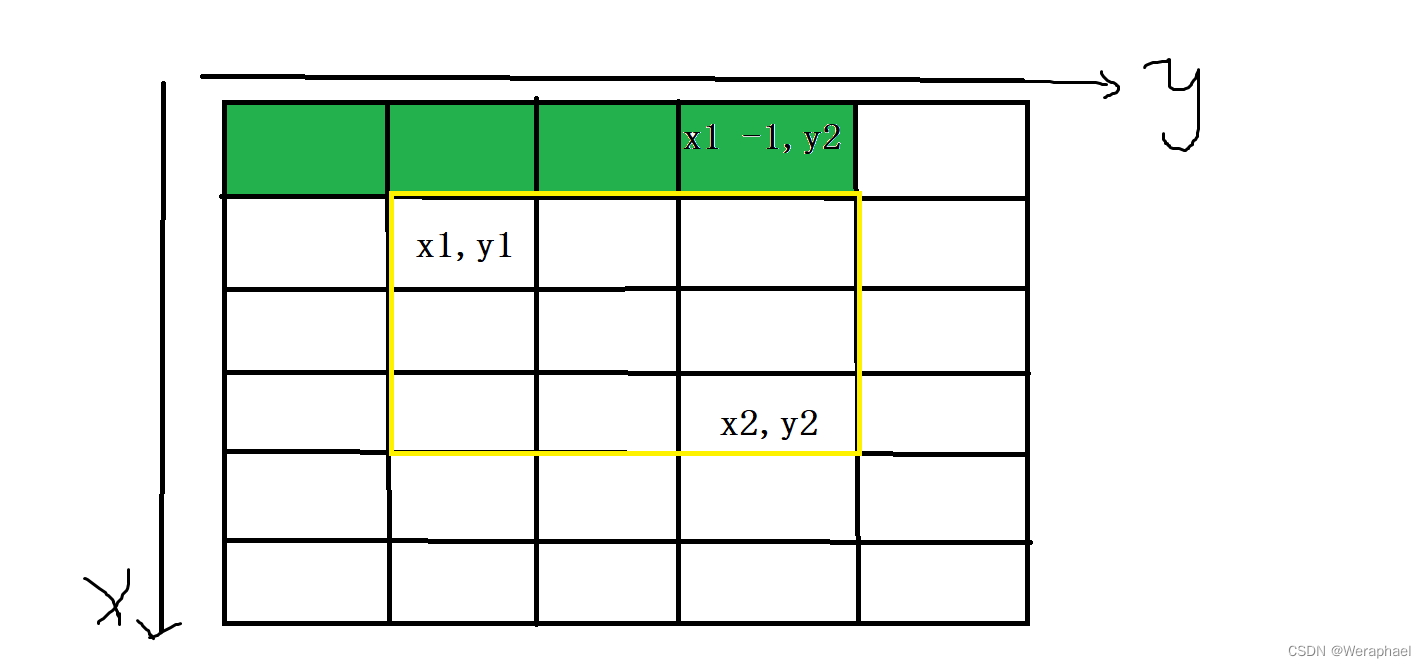
列出式子:
S = S[x2][y2] - S[x1 - 1][y2] - ...
- 第三步,再减去灰色部分所有数的和
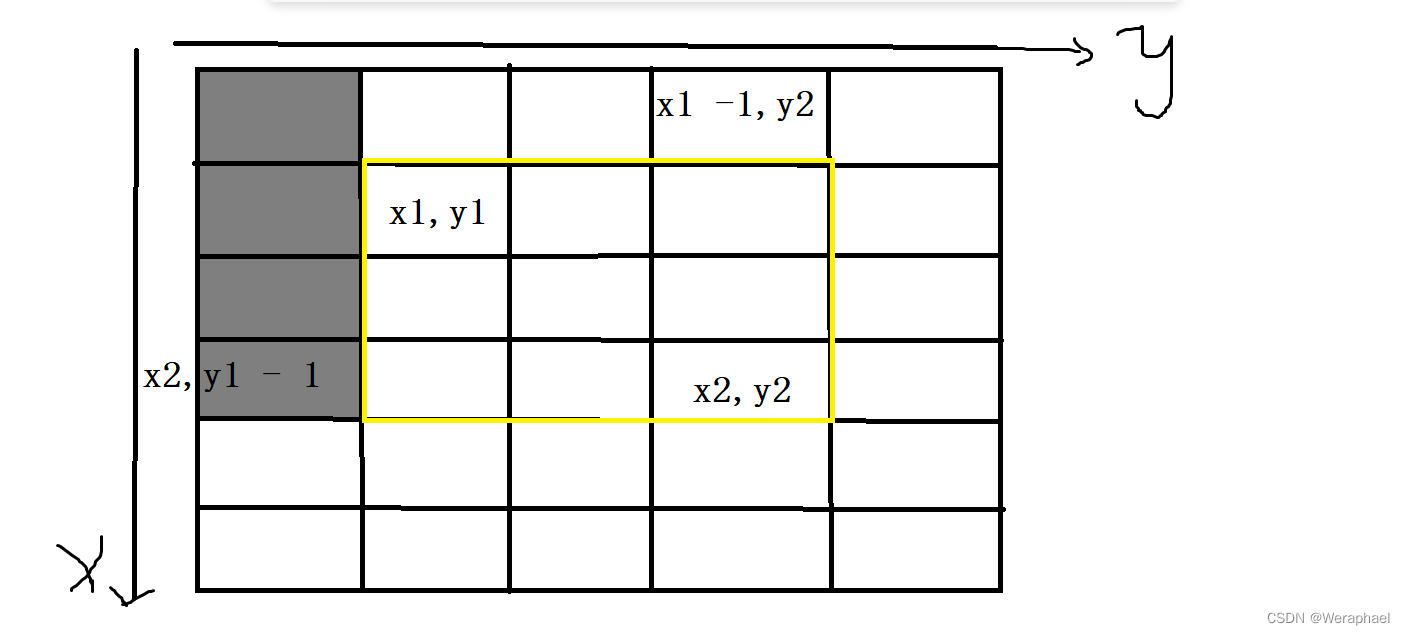
列出式子:
S = S[x2][y2] - S[x1 - 1][y2] - S[x2][y1 - 1] + ...
- 第四步去重,因为前两部重复减去了紫色部分所有数的和,因此要加上一次
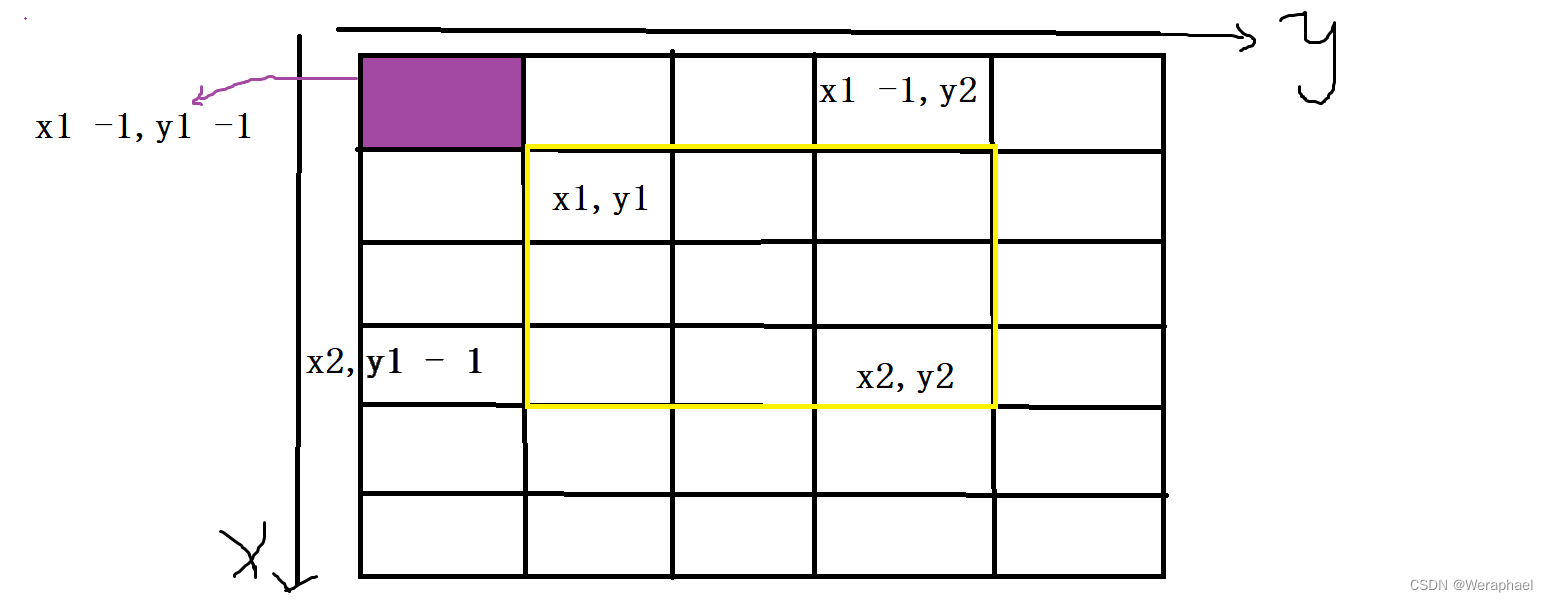
列出式子:
S = S[x2][y2] - S[x1 - 1][y2] - S[x2][y1 - 1] + S[x1 - 1][y1 - 1]
2.4 代码模板
#include <iostream>
using namespace std;const int N = 10010;
int n, m;
int a[N][N],s[N][N];int main()
{scanf("%d%d%d", &n, &m); //n -行 m - 列//输入数组for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )scanf("%d", &a[i][j]);//二维前缀和公式for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];//求子矩阵int x1, y1, x2, y2;scanf("%d%d%d%d", &x1, &y1, &x2, &y2);printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);return 0;
}三、总结
其实大家只要背下前缀和公式就好了
- 一维前缀和公式:
S[i]= S[i-1] + a[i] - 求某段区间
[l,r]:S[r]- S[l-1]
- 二维前缀和公式:
S[i][j] = S[i][j-1] + S[i-1][j] - S[i-1][j-1] + a[i][j] - 求子矩阵公式:
S = S[x2][y2] - S[x1 - 1][y2] - S[x2][y1 - 1] + S[x1 - 1][y1 - 1]
相关文章:

【算法基础】一维前缀和 + 二维前缀和
👦个人主页:Weraphael ✍🏻作者简介:目前正在学习c和算法 ✈️专栏:【C/C】算法 🐋 希望大家多多支持,咱一起进步!😁 如果文章有啥瑕疵 希望大佬指点一二 如果文章对你有…...
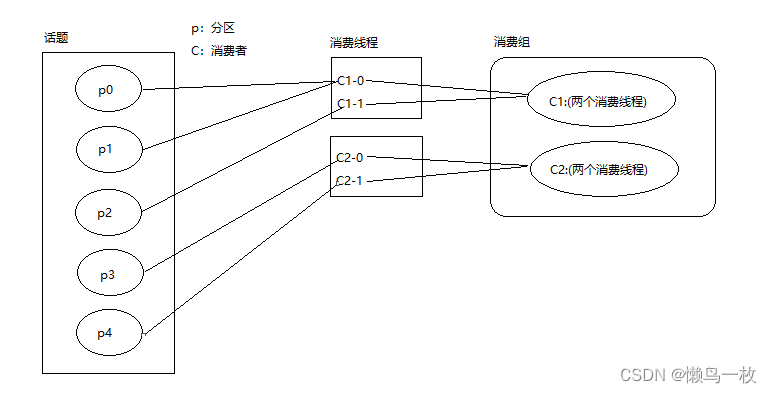
Kafka消费分组和分区分配策略
Kafka消费分组,消息消费原理 同一个消费组里的消费者不能消费同一个分区,不同消费组的消费组可以消费同一个分区 (即同一个消费组里面的消费者只能在一个分区中) Kafka分区分配策略 问题 用过 Kafka 的同学用过都知道…...
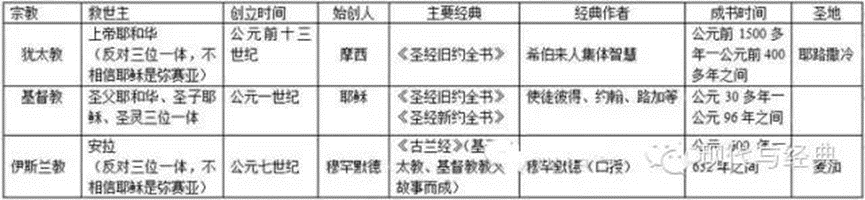
犹太教、基督教、伊斯兰教的区别与联系
一、犹太教、基督教、伊斯兰教的简明关系图二、犹太教、基督教、伊斯兰教的主要区别注:弥赛亚(希伯莱语)就是基督(希腊语),意思是“救世主”。注:伊斯兰教的观点是:穆罕默德不是伊斯…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 打印文件(Python) | 机试题+算法思路+考点+代码解析 【2023】
打印文件 题目 有 5 台打印机打印文件,每台打印机有自己的待打印队列。 因为打印的文件内容有轻重缓急之分,所以队列中的文件有1~10不同的优先级,其中数字越大优先级越高。 打印机会从自己的待打印队列中选择优先级最高的文件来打印。 如果存在两个优先级一样的文件,则选…...
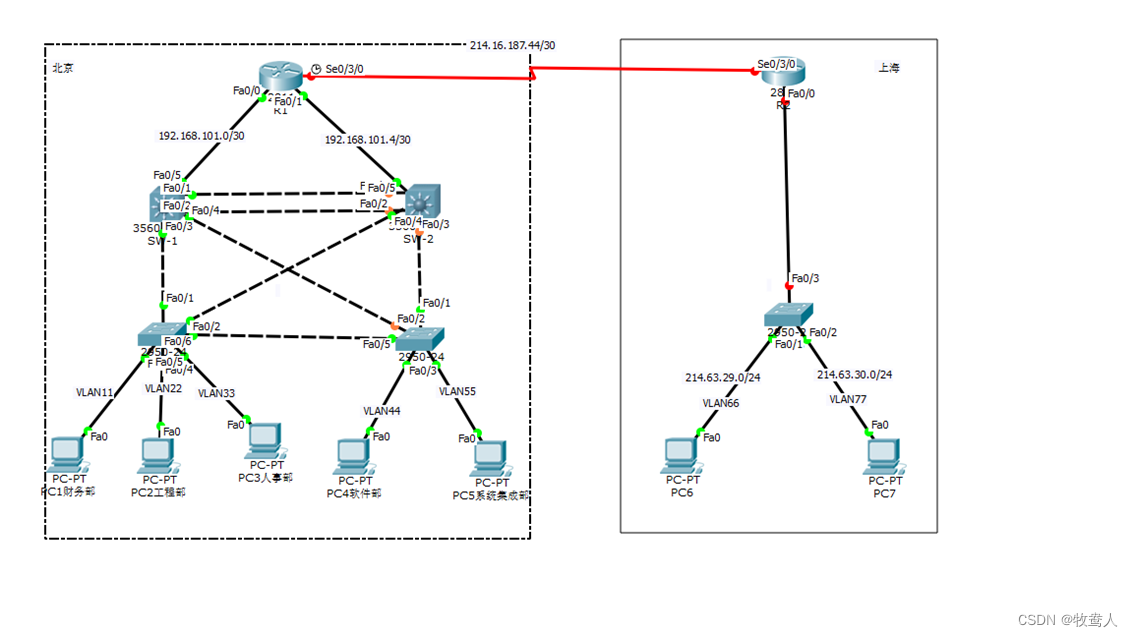
网络工程师必备知识点
作为网络工程师,您将负责设计、部署和维护计算机网络系统。这包括构建、配置和管理网络设备,如交换机、路由器、防火墙等,并确保网络系统能够高效地运行。您需要了解计算机网络的各个层次、协议、标准和技术,包括TCP/IP、DNS、HTT…...

数据在内存中的存储【下篇】
文章目录⚙️3.浮点型在内存中的存储🔩3.1.一个例子🔩3.2.浮点数的存储规则🔩3.3.例题解析⚙️3.浮点型在内存中的存储 🔩3.1.一个例子 🔴浮点数存储的例子:👇 int main() {int n 9;float* …...

前端开发项目规范写法介绍
1. 基本原则 结构、样式、行为分离 尽量确保文档和模板只包含 HTML 结构,样式都放到样式表里,行为都放到脚本里。 缩进 统一两个空格缩进(总之缩进统一即可),不要使用 Tab 或者 Tab、空格混搭。 文件编码 使用不带 BOM 的 UTF-8 编码。 在 HTML中指定编码 <meta c…...

百万医疗险是什么
一、百万医疗险是什么 从名字可以看出,这是一款医疗险。因为保额高,最高能报销百万,所以叫百万医疗险。 二、百万医疗险有什么用 可以报销被保险人因意外伤害和疾病导致的医疗费用 三、如何挑选 虽然高达几百万的保额,但保额却并非…...

矩阵中的路径 AcWing (JAVA)
请设计一个函数,用来判断在一个矩阵中是否存在一条路径包含的字符按访问顺序连在一起恰好为给定字符串。 路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。 如果一条路径经过…...

使用终端工具给你的电脑发送弹窗提醒
大家好,我是良许。 现在人手一部智能手机,这些智能手机都有个非常实用的功能,那就是弹窗提醒。当我们收到短信,或者微信信息时,手机就会弹窗显示信息的大致内容。有了这个功能你就不会错过重要信息了。 电脑上也有类…...
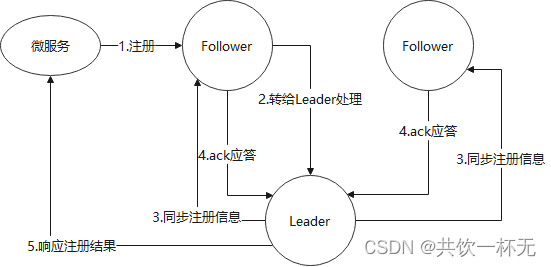
SpringCloud Alibaba 之Nacos集群部署-高可用保证
文章目录Nacos集群部署Linux部署docker部署(参考待验证)Nacos 集群的工作原理Nacos 集群中 Leader 节点是如何产生的Nacos 节点间的数据同步过程官方推荐用户把所有服务列表放到一个vip下面,然后挂到一个域名下面。http://nacos.com:port/ope…...
Scala集合详解(第七章:集合、数组、列表、set集合、map集合、元组、队列、并行)(尚硅谷笔记)
集合第七章:集合7.1 集合简介7.1.1 不可变集合继承图7.1.2 可变集合继承图7.2 数组7.2.1 不可变数组7.2.2 可变数组7.2.3 不可变数组与可变数组的转换7.2.4 多维数组7.3 列表 List7.3.1 不可变 List7.3.2 可变 ListBuffer7.4 Set 集合7.4.1 不可变 Set7.4.2 可变 mutable.Set7.…...
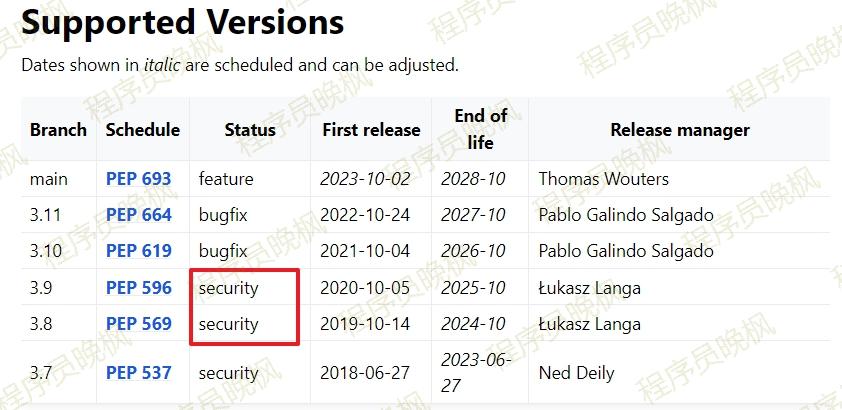
定了:Python3.7,今年停止更新~
大家好,这里是程序员晚枫。 今天给大家分享一个来自Python官网的重要消息:Python3.7马上就要停止维护了,请不要使用了! 官网链接:https://devguide.python.org/versions/ 停更的后果是什么? 周末翻阅Py…...
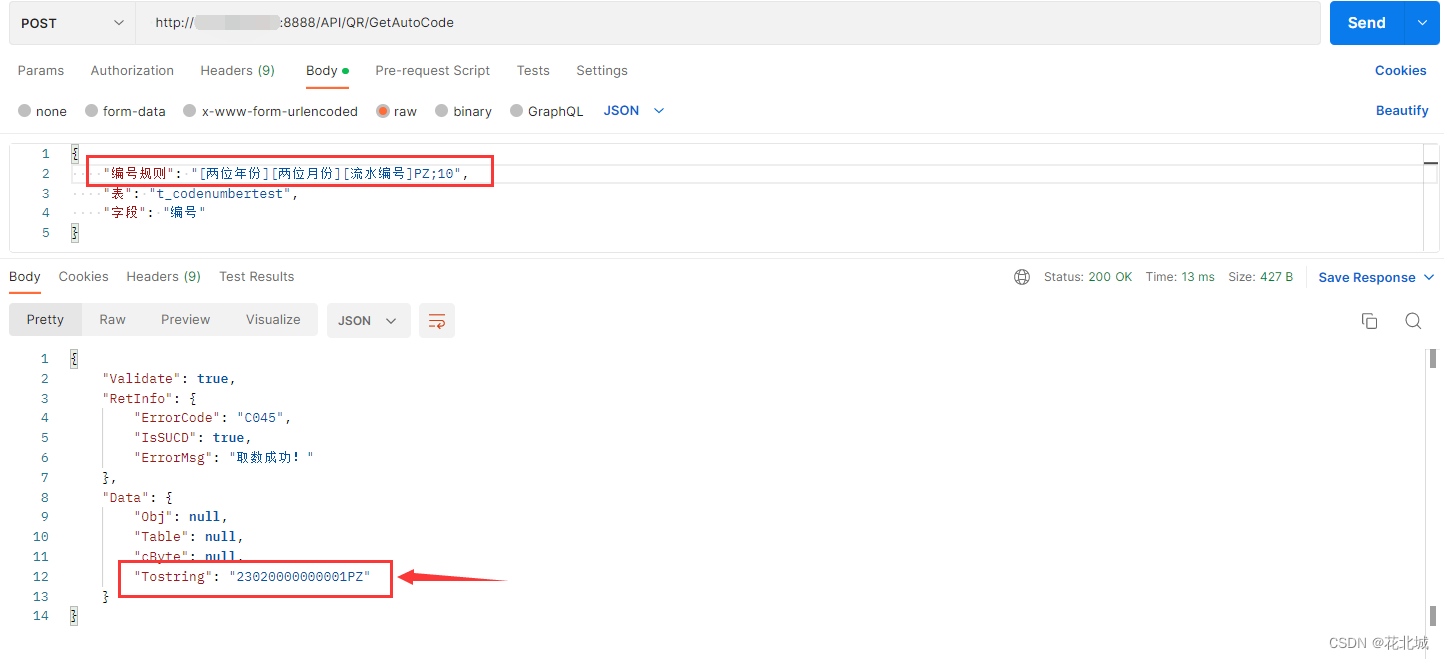
C# 业务单据号生成器(定义规则、获取编号、流水号)
系列文章 C#底层库–数据库访问帮助类(MySQL版) 本文链接:https://blog.csdn.net/youcheng_ge/article/details/126886379 C#底层库–JSON帮助类_详细(序列化、反序列化、list、datatable) 本文链接:htt…...
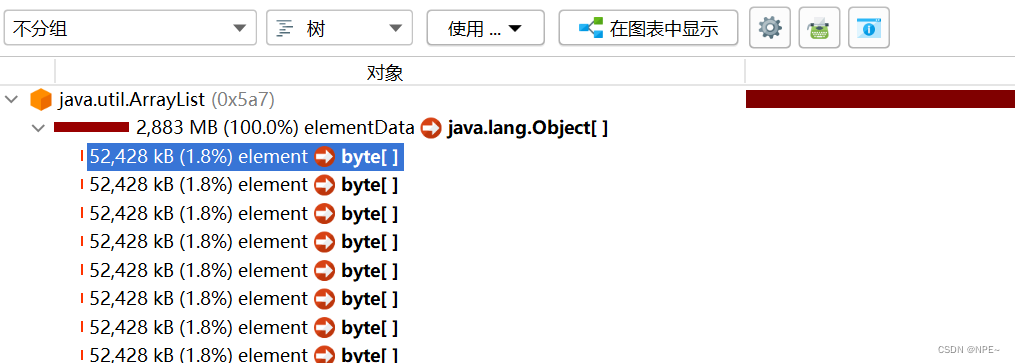
Java的dump文件分析及JProfiler使用
Java的dump文件分析及JProfiler使用 1 dump文件介绍 从软件开发的角度上,dump文件就是当程序产生异常时,用来记录当时的程序状态信息(例如堆栈的状态),用于程序开发定位问题。 idea配置发生OOM的时候指定路径生成dump文件 # 指定…...
sympy高斯光束模型
文章目录Gauss模型sympy封装实战sympy.phisics.optics.gaussopt集成了高斯光学中的常见对象,包括光线和光学元件等,有了这些东西,就可以制作一个光学仿真系统。Gauss模型 高斯光束的基本模型为 E(r,z)E0ω0ω(z)exp[−r2ω2(z)]exp[−ik…...
Cloudflared 内网穿透 使用记录
Cloudflared 内网穿透前提创建cloudflared tunnel我使用的服务前提 你必须要有一个域名,并且可以改域名的dns解析服务商到cloudflare 1.登录到cloudflare后台,点击添加站点 2.输入自己的域名,下一步选择免费套餐 3.他会搜索这个域名下已有…...

柴油发电机组的调压板
1 概述 柴油发电机组的调压板是一种用于控制发电机输出电压的装置。它通常由一块电子电路板和一个电子电路板上的电位器组成。 当发电机运行时,它会产生电压,然后通过调压板中的电路进行控制。调压板中的电路会检测输出电压的大小,并通过电…...

【MySQL】表操作和库操作
文章目录概念库操作1.创建数据库2.删除数据库3.选择数据库4.显示数据库列表表操作1.创建数据表CREATE2.删除数据表DROP3.插入数据INSERT4.更新数据UPDATE5.修改数据ALTER6.查询数据SELECT7.WHERE子句8.ORDER BY子句9.LIMIT子句10.GROUP BY子句11.HAVING子句使用注意事项概念 M…...

拓扑排序的思想?用代码怎么实现
目录 一、拓扑排序的思想 二、代码实现(C) 代码思想 核心代码 完整代码 一、拓扑排序的思想 以西红柿炒鸡蛋这道菜为例,其中的做饭流程为: 中间2 6 3 7 4的顺序都可以任意调换,但1和5必须在最前面,这是…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...
