MATLAB中M文件编写
简介
所谓M文件就是将处理问题的各种命令融合到一个文件中,该文件以.m为扩展名。然后,由MATLAB系统编译M文件,得出相应的运行结果。M文件具有相当大的可开发性和扩展性。M文件有脚本文件和函数文件两种。脚本文件不需要输入参数,也不输出参数,而会按照文件中指定的顺序执行命令序列。而函数文件则接受其他数据为输入参数,并且可以返回结果。
脚本式M文件
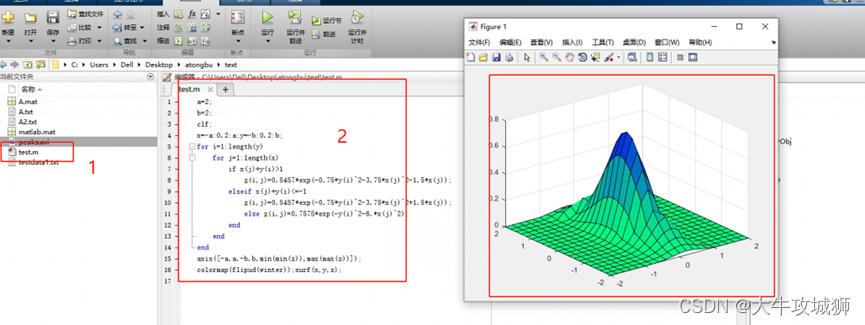
避免用户输入较多命令,避免重复输入命令,打开该类M文件,单击运行或者按下F5按键,即可运行该类文件
a=2;
b=2;
clf;
x=-a:0.2:a;y=-b:0.2:b;
for i=1:length(y)for j=1:length(x)if x(j)+y(i)>1z(i,j)=0.5457*exp(-0.75*y(i)^2-3.75*x(j)^2-1.5*x(j));elseif x(j)+y(i)<=-1z(i,j)=0.5457*exp(-0.75*y(i)^2-3.75*x(j)^2+1.5*x(j));else z(i,j)=0.7575*exp(-y(i)^2-6.*x(j)^2);endend
end
axis([-a,a,-b,b,min(min(z)),max(max(z))]);
colormap(flipud(winter));surf(x,y,z);运行结果,参考如下图片
函数式M文件
函数式M文件比脚本式M文件相对复杂一些,脚本式M文件不需要输入变量,也不一定返回结果,而函数式M文件一般要输入变量,并且有返回结果。举例使用M文件计算向量的平均值。
输入如下代码,保存average.m
function y = average(x)
% AVERAGE Mean of vector elements.
% AVERAGE(X), where X is a vector, is the mean of vector
% elements. Nonvector input results in an error.
[m,n] = size(x);
if (~((m == 1) | (n == 1)) | (m == 1 & n == 1))error('Input must be a vector') % 错误信息
end
y = sum(x)/length(x); 调用过程
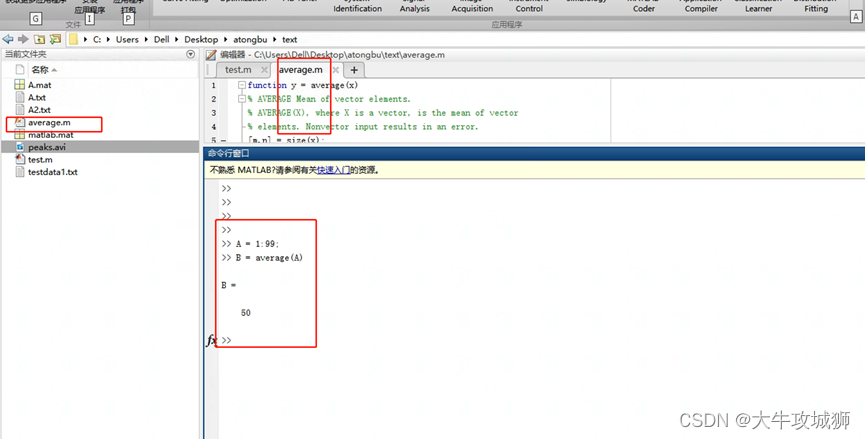
A = 1:99
B = average(A)
结果如下图所示

实际代码存放以及编写如下图所示
相关文章:

MATLAB中M文件编写
简介 所谓M文件就是将处理问题的各种命令融合到一个文件中,该文件以.m为扩展名。然后,由MATLAB系统编译M文件,得出相应的运行结果。M文件具有相当大的可开发性和扩展性。M文件有脚本文件和函数文件两种。脚本文件不需要输入参数,…...
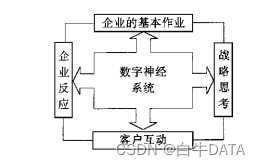
企业数字化神经网络
随着数字化时代的到来,数据已经成为企业战略性资源和重要的生产要素。企业数字化转型的核心是充分开发和利用数据资源,以数据为驱动,对业务流程进行重构与创新,从而提升企业的核心竞争力。业务系统是企业数据资源的源头࿰…...

C++this指针
本文旨在讲解C中this关键字,以及其相关作用! 定义 this 是 C 中的一个关键字,也是一个 const 指针,它指向当前对象,通过它可以访问当前对象的所有成员。 this的介绍 下面来看一下关于this这个关键字的实例࿰…...
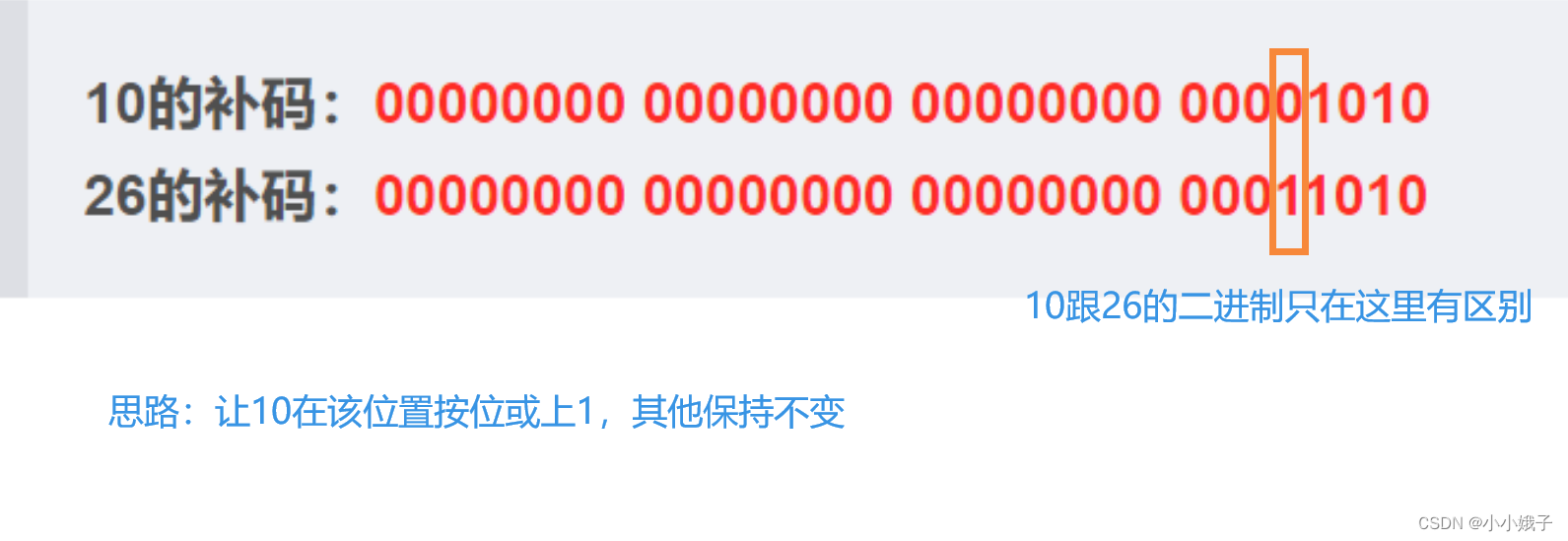
【初阶C语言】操作符1--对二进制的操作
前言:本节内容介绍的操作符,操作的对象是二进制位。所以前面先介绍整数的二进制位 一、二进制位介绍 1.二进制介绍 (1)整数的二进制表示形式有三种:原码、反码和补码。 (2)原码、反码和补码的…...

安装pyscipopt
安装pyscipopt Conda会自动安装SCIP,因此所有内容都可以通过单个命令安装: GitHub - scipopt/PySCIPOpt: Python interface for the SCIP Optimization Suite conda create --name myenv python3.8 # 创建新环境 conda activate myenv # 激活新环境 …...
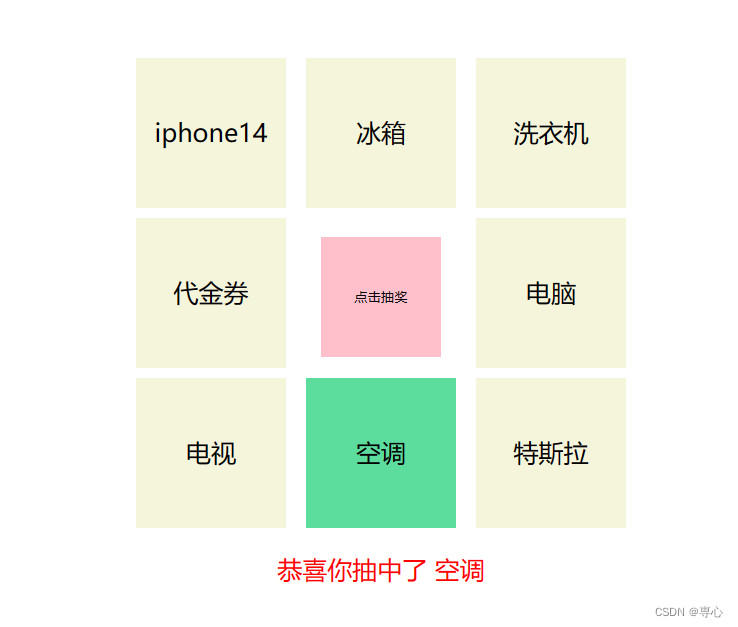
原生js实现的轮盘抽奖案例
来到大学也是有二年了,吃饭最多的地方就是在食堂,经过这么久的时间,已经几乎是把每个窗口的菜都吃腻了,所以我打算做个轮盘抽奖的形式来决定我每天要吃些什么。 目录 实现效果图: 静态搭建 js代码 1.实现此功能的思路…...
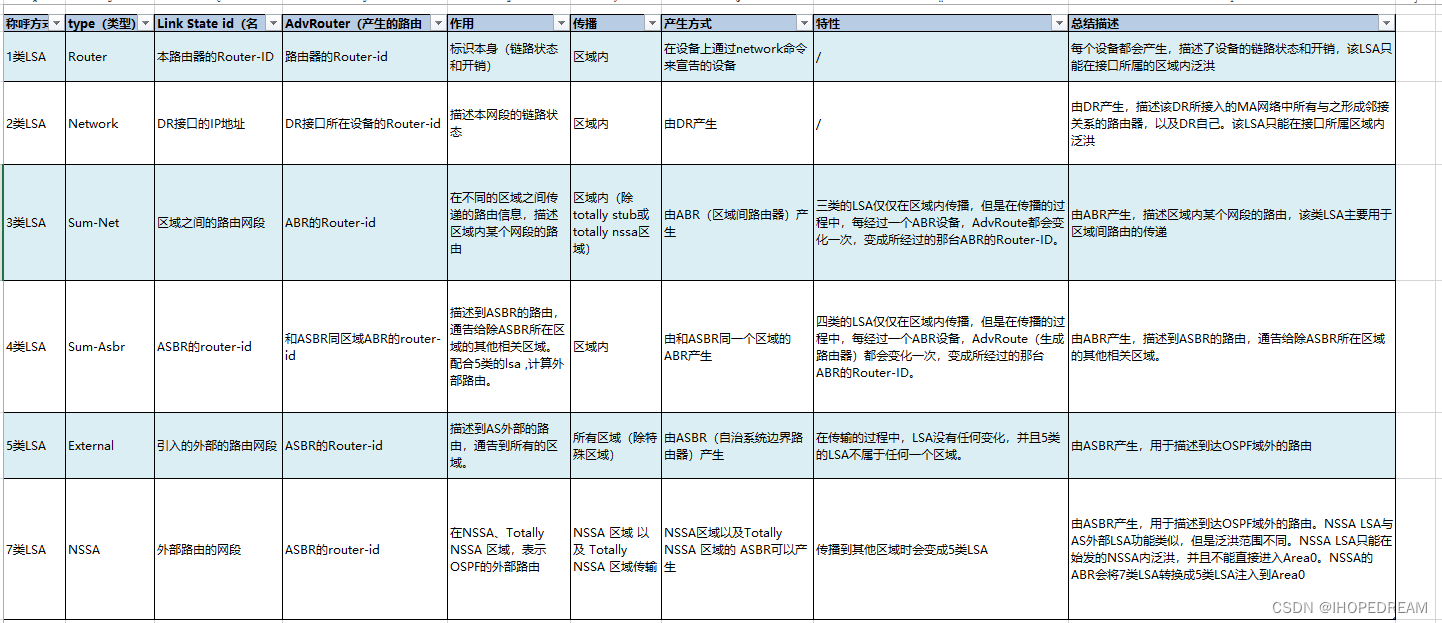
最经典的解析LSA数据库(第六课)
初步认识OSPF的大致内容(第三课)_IHOPEDREAM的博客-CSDN博客 1 OSPF 工作过程 建立领居表 同步数据库 今天来 说一说数据库概念 计算路由表 2 什么是数据库? 数据库是一个组织化的数据集合,用于存储、管理和检索数据。它是一个可访问的集合&#x…...
C++基础入门
文章目录 前言一、C历史及发展1.C是什么2.C历史 二、开始C1.基础类型1.第一个简单的C程序2.命名空间1.命名空间的介绍2.命名空间的使用3.命名空间的using声明与using指示 3.初识输入输出操作4.引用1.引用概念2.引用的使用1.引用做参数2.引用做返回值 3.引用和指针的区别4.const…...
)
【每日随笔】驾驭人性 ② ( 员工立场问题 | 立场转变 | 吴越同舟 | 老板如何与员工结成利益共同体 )
文章目录 一、员工立场问题二、立场转变三、吴越同舟四、老板如何与员工结成利益共同体 一、员工立场问题 人的潜力是很大的 , 肩上抗 100 斤 水泥 和 肩上抗 100 斤黄金 , 能一样吗 , 扛着黄金绝对能扛回家 ; 员工 不愿意 与公司一条心是正常的 , 员工 拿的是 死工资 , 公司赚…...
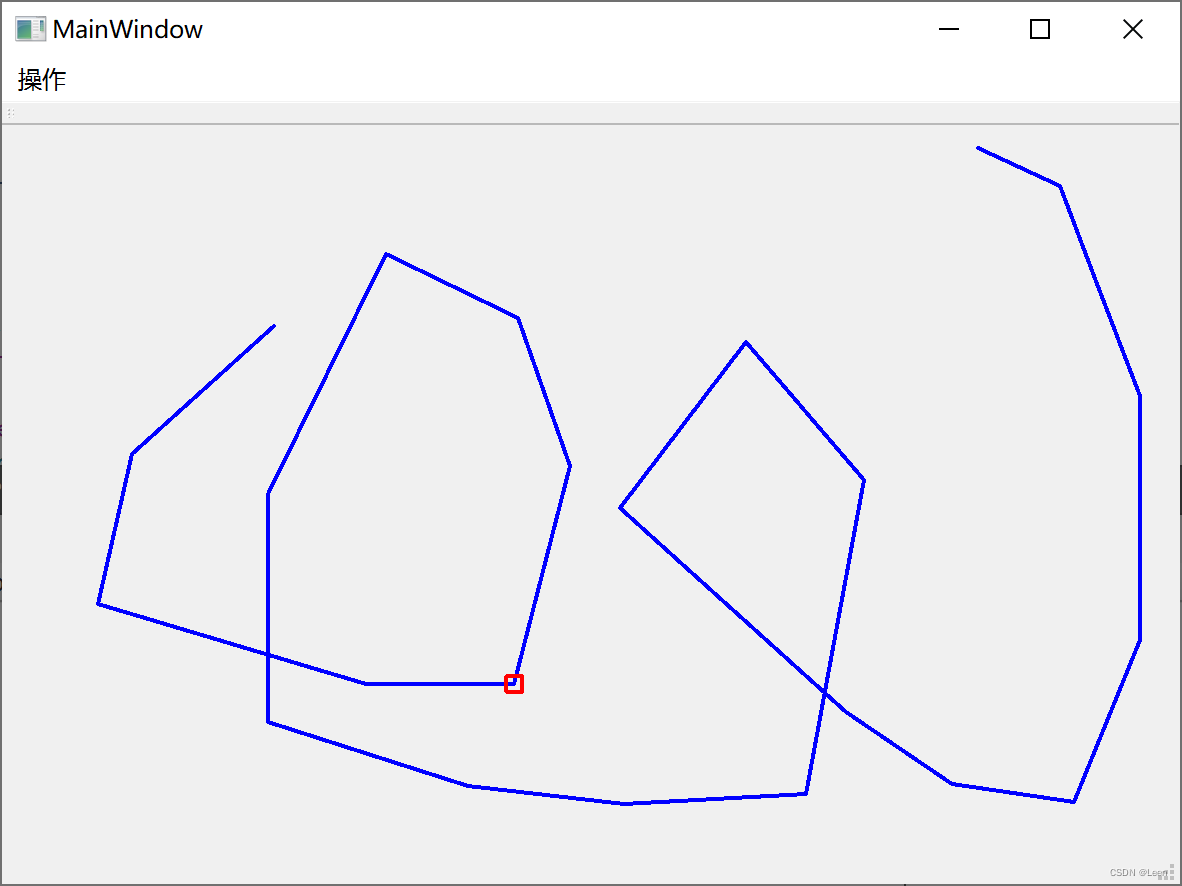
C++(QT)画图行车
通过鼠标在窗口上点击形成多个点的连线,绘制一辆汽车沿着绘制的连线轨迹前进。要求连线点数大于20.可以通过清除按钮清除已经绘制的连线,并可以重新绘制一条轨迹连线。当车辆行驶到轨迹终点时,自动停止。(汽车实在可用方块代替&am…...

Unity中Shader抓取屏幕并实现扭曲效果(优化)
文章目录 前言一、在之前顶点着色器的输入中,放弃了使用结构体传入,而是直接从应用程序阶段传入参数,这样写的话,对于程序来说,不方便扩张,所以需要对其进行修改实现1、定义结构体用于传入顶点坐标系2、因为…...
)
肖sir__设计测试用例方法之_(白盒测试)
白盒测试技术 一、定义: 白盒测试也叫透明盒测试,检查程序内部结构及路径一是否符合规格说明,二是否符合其代码规范。 因此,也叫结构测试或者逻辑驱动测试。 二、白盒测试常见方法: a、语句覆盖; b、判断覆…...
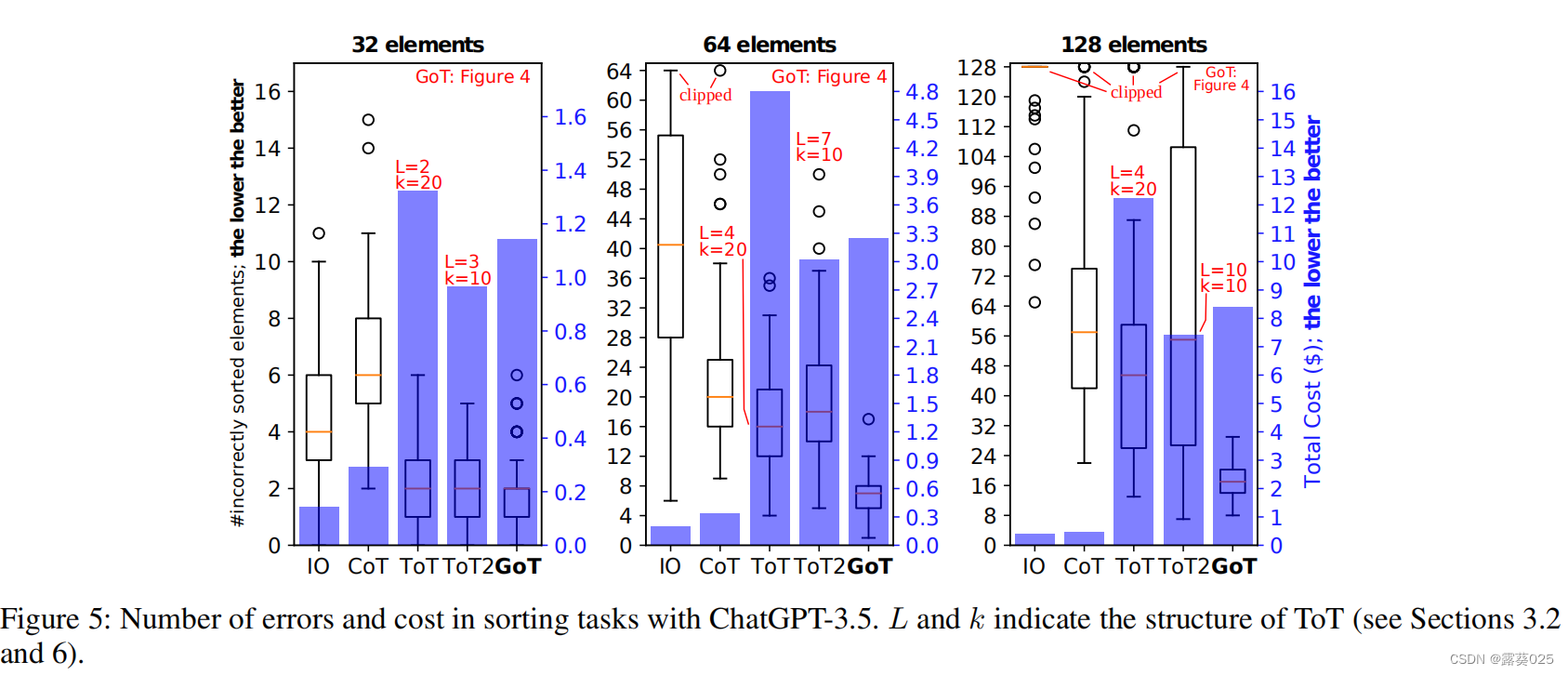
GoT:用大语言模型解决复杂的问题
GoT:用大语言模型解决复杂的问题 摘要介绍背景和符号表示语言模型和上下文学习Input-Output(IO)Chain of thought(CoT)Multiple CoTTree of thoughts(ToT) GoT框架推理过程思维变换聚合变换&…...

nginx服务和uwsgi服务如何设置开机自启动
上次学到了在云服务器下如何部署Django项目,用到了nginx服务和uwsgi服务,需要手工启动这2个服务的命令。 现在考虑如何设置开机自启动,为什么要这样考虑?因为服务器万一出问题,意外重启了,那我们部署的Dja…...

算法-分治算法
文章来源: https://blog.csdn.net/weixin_45630258/article/details/126425400 欢迎各位大佬指点、三连 一、分治 1、定义:分治,也就是分而治之。 它的一般步骤是: ① 将原问题分解成若干个规模较小的子问题(子问题…...

react 实现监听逻辑
需求: 在一个页面下有多个子tab在某些tab 下,或者父节点的数据更新的时候,其他子tab 或者父节点也要同步更新 进程: 正常情况下会把所有用到的数据都移动到父节点,修改行为也都放在父节点但如果这样的话父节点的数据…...

vue项目一个页面包含多个时间选择器的处理方案
描述:vue项目中如果在一个页面使用多个时间选择器组件时,不同的时间选择器需要分别分开工作 解决方案一 原本是想直接每一个时间选择器都安排一套相对独立的维生系统,但是到后面发现繁琐至极,而且报错,果断放弃&#…...
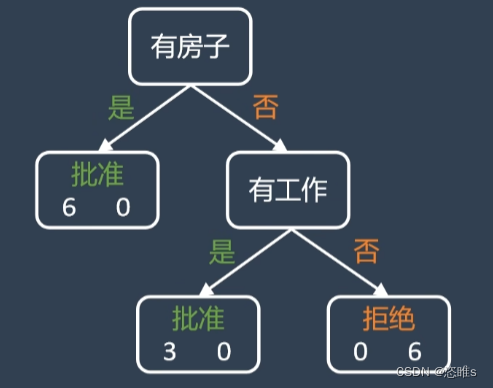
机器学习入门教学——决策树
1、简介 决策树算法是一种归纳分类算法,它通过对训练集的学习,挖掘出有用的规则,用于对新数据进行预测。决策树算法属于监督学习方法。决策树归纳的基本算法是贪心算法,自顶向下来构建决策树。 贪心算法:在每一步选择…...

文献阅读:Chain-of-Thought Prompting Elicits Reasoning in Large Language Models
文献阅读:Chain-of-Thought Prompting Elicits Reasoning in Large Language Models 1. 文章简介2. 具体方法3. 实验结果 1. 数学推理 1. 实验设计2. 实验结果3. 消解实验4. 鲁棒性考察 2. 常识推理 1. 实验设计2. 实验结果 3. 符号推理 1. 实验设计2. 实验结果 4.…...

从零开发一款ChatGPT VSCode插件
本文作者是360奇舞团开发工程师 引言 OpenAI发布了ChatGPT,就像是给平静许久的互联网湖面上扔了一颗重磅炸弹,刹那间所有人都在追捧学习它。究其原因,它其实是一款真正意义上的人工智能对话机器人。它使用了深度学习技术,通过大…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
