论文阅读:Distortion-Free Wide-Angle Portraits on Camera Phones
论文阅读:Distortion-Free Wide-Angle Portraits on Camera Phones
今天介绍一篇谷歌 2019 年的论文,是关于广角畸变校正的。
Abstract
广角摄影,可以带来不一样的摄影体验,因为广角的 FOV 更大,所以能将更多的内容拍摄进画面,在多人集体合影的时候,一般用广角可以将大家都拍到,但是广角摄影也有弊端,最显著的问题就是畸变,随着 FOV 的增加,画面边缘的人很容易发生变形,比如人头,身体被拉伸。这种畸变让画面边缘的人与真实的人差异很大。这篇论文就是为了解决广角摄影下的畸变问题的。给定一张广角下的人像照,文章中的算法是通过构建一个能量优化函数,将球极投影下的人脸区域与透视投影下的背景区域的位移 mesh 进行联合优化,从而达到一个畸变校正的目的。这篇文章里的算法最后应该是用到了谷歌的 Pixel 手机中了。
Introduction
文章中首先提到了畸变的几种成因, camera 成像是遵循透视投影规律的,透视成像投影的规律就是近大远小,同时视场边缘的成像随着入射角的增加,会产生更大的透视形变,这种形变是由透视投影的客观规律产生的,无法避免。此外镜头本身也会有光学畸变,这是属于光学像差的一种,FOV 越大的镜头,这种光学畸变也会越明显,光学畸变会导致直线弯曲,不过相比透视畸变,镜头的光学畸变有比较成熟的校正方法,比如经典的张正友校正法,通过标定棋盘格,可以估计出镜头的畸变参数,从而进行镜头的光学畸变校正。
不过,即使进行了镜头的光学畸变校正,成像的透视畸变依然存在,所以这篇文章主要是为了解决镜头的透视畸变问题,作者在文章中也提到,他们提出的方法也属于与内容相关的 warping 方法,这类方法之前也广泛地应用于各种图像的操作中,比如全景的拼接,广角的畸变校正,防抖等。本文主要聚焦于人脸区域的 warp,作者认为对于人像摄影来说,用户对人脸的形状是最敏感的。
Method
文章的方法,看起来流程比较简单,如下所示:

给定一张输入图片,首先是用一个分割模型,将人脸区域分割出来;然后将人脸区域进行球极投影;接着利用一个能量函数,将球极投影后的人脸区域 mesh 与背景区域的 mesh 进行优化,使得人脸区域与背景区域的 mesh 能够平滑过度,最终利用输出的 mesh 对全图进行 warp,这样就得到了校正后的图像。
Subject Mask Segmentation
人脸区域分割,这个已经非常成熟了,有很多的分割模型都可以做到这一点。这里就不多做介绍了。
Stereographic Projection
这篇文章对人脸区域的校正利用了一种称为 Stereographic Projection,也就是球极投影,球极投影是一种将 3D 物体投影到 2D 平面的投影方式,这种投影方式可以最大限度的保持物体的形状,不过代价就是会让直线变得弯曲,文章也给出了几种不同投影的例子

可以看到,对于一张有透视畸变的图像,人像的脸已经有明显的拉伸,通过 Stereographic projection 或者 Mercator projection,人脸得到比较好地校正,但是背景的直线已经产生了明显的弯曲,这就类似一种鱼和熊掌不可兼得的感觉,你想保证背景直线是直的,人脸区域会被拉伸,类似输入图;反过来,你想让人脸区域得到校正,背景直线又变得弯曲。所以文章作者想到了一种联合优化的方式,这个后面详细介绍,先来看看球极投影到底是个啥。
文章给出的球极投影的定义如下:
r u = r 0 tan ( 0.5 arctan ( r p f ) ) (1) r_u = r_0 \tan (0.5 \arctan(\frac{r_p}{f})) \tag{1} ru=r0tan(0.5arctan(frp))(1)
其中 f f f 是镜头的焦距, r u , r p r_u, r_p ru,rp 分别表示球极投影以及透视投影下以镜头中心作为参考的半径, r 0 r_0 r0 表示一个 scale 系数,保证两种投影下面图像边缘的所对应的半径是相等的
r 0 = d 2 tan ( 0.5 arctan ( d 2 f ) ) (2) r_0 = \frac{d}{2 \tan (0.5 \arctan(\frac{d}{2f}))} \tag{2} r0=2tan(0.5arctan(2fd))d(2)
其中, d = min { W , H } d = \min\{W, H\} d=min{W,H},表示图像宽高中的较小值。
Mesh Placement
接下来介绍 mesh 的构建,mesh 可以看成是一个网格图,一个 mesh 包含一组网格点 { v i } \{ \mathbf{v}_i \} {vi}, v i \mathbf{v}_i vi 是一个向量,表示网格点对应的二维坐标,假设输入图对应的 mesh 图是 { p i } \{ \mathbf{p}_i \} {pi},对输入图 mesh 上的每个网格点应用球极变换,可以得到一组新的网格点,以及一个新的 mesh, { u i } \{ \mathbf{u}_i \} {ui},这两个 mesh 对应网格点的坐标差,其实就是位移向量场,通过这个位移向量场,可以进行 warp,不过正如前面所说,如果直接 warp,人脸区域虽然得到了校正,但是背景会产生扭曲。当然,一种最直观的方法,就是将人脸区域的 mesh 与背景区域的 mesh 分开处理,人脸区域的 mesh 用球极投影下的 mesh,而背景区域依然用之前输入的 mesh。如下式所示:
w i = { 0 if p i ∉ face mask 1 if p i ∈ face mask (3) w_i = \begin{cases} 0 \quad \text{if} \quad \mathbf{p}_i \notin \text{face mask} \\ 1 \quad \text{if} \quad \mathbf{p}_i \in \text{face mask} \\ \end{cases} \tag{3} wi={0ifpi∈/face mask1ifpi∈face mask(3)
不过这种方式依然会有问题,文章也给出了示意图,这种直接粗暴地分成两部分的方式,也会到底非常明显的 artifacts
Local Face Undistortion
为了解决这个问题,文章作者提出了一种能量优化的方式,文章中构造了一个如下的能量优化函数:
v i ∗ = argmin v i E t ( v i ) (4) \mathbf{v_{i}^{*}} = \text{argmin}_{\mathbf{v_{i}}} E_t(\mathbf{v_{i}}) \tag{4} vi∗=argminviEt(vi)(4)
E t E_t Et 可以认为是几种不同的能量函数的加权和。
Face Objective Term
首先是人脸区域的能量项,每个人脸区域都构建一个能量项,所有人脸区域的能量项求和,可以得到整体的人脸区域的能量项
E f = ∑ k E s , k (5) E_f = \sum_{k} E_{s, k} \tag{5} Ef=k∑Es,k(5)
其中, k k k 表示输入图中人脸的编号,可以看到,这个能量项是对每个人脸区域单独构建的,有多少个人脸,就会构建多少个能量项,每个能量项的定义如下:
E s , k = ∑ i ∈ B k w i m i ∥ v i − ( S k u i + t k ) ∥ 2 2 + λ ( S k ) (6) E_{s,k} = \sum_{i\in\mathbf{B}_k} w_i m_i \left \| \mathbf{v}_i - (\mathbf{S_k \mathbf{u}_i + \mathbf{t}_k}) \right \|_{2}^{2} + \lambda(\mathbf{S}_k) \tag{6} Es,k=i∈Bk∑wimi∥vi−(Skui+tk)∥22+λ(Sk)(6)
其中, w i w_i wi 表示公式 (3) 定义的权重, { u i } \{ \mathbf{u}_i \} {ui} 表示球极投影 mesh 上的网格点, { B k } \{ \mathbf{B}_k \} {Bk} 表示第 k 个人脸区域中的网格点,因为图像不同区域的畸变程度不同,需要校正的强度也就不同,所以上面的能量项还加了一个 m i m_i mi 来调整权重,这个 m_i 服从一个径向函数的分布
m i ∼ 1 1 + exp ( ( − ( r − r a ) / r b ) ) m_i \sim \frac{1}{1 + \exp((-(r-r_a)/r_b))} mi∼1+exp((−(r−ra)/rb))1
其中, r r r 表示输入图像中的半径, r a , r b r_a,r_b ra,rb 是两个超参,用来控制强度的,对于图像中心的点,保证 m i = 0.01 m_i = 0.01 mi=0.01,对于图像边缘的点,保证 m i = 1.0 m_i=1.0 mi=1.0。从公式 (6) 可以看出,虽然文章是用球极投影来解决人脸的畸变,但是最终优化的时候,并不是简单地直接用球极投影的网格点,而是用了一个仿射变换来拟合,
S k = [ a k b k − b k a k ] t k = [ t k 1 t k 2 ] (7) \mathbf{S}_k = \begin{bmatrix} a_k & b_k \\ -b_k & a_k \end{bmatrix} \quad \mathbf{t}_k = \begin{bmatrix} t_{k1} \\ t_{k2} \end{bmatrix} \tag{7} Sk=[ak−bkbkak]tk=[tk1tk2](7)
这个仿射变换,可以让每个人脸区域的球极投影有更大的自由度,在球极投影的基础上,进行适当的自适应调整。公式 (7) 中的 a k a_k ak 是一个缩放系数,文章作者加了一个正则项来控制这个系数:
λ ( S k ) = w s ∥ a k − s t ∥ 2 2 (8) \lambda(\mathbf{S}_k) = w_s \left \| a_k - s_t \right \|_{2}^{2} \tag{8} λ(Sk)=ws∥ak−st∥22(8)
文章中设置的 w s = 2000 , s t = 1 w_s = 2000, s_t = 1 ws=2000,st=1
Line-Bending Term
人脸区域的能量项介绍完了,下面看看背景区域的能量项,文章中设置了一个能量项来保证让直线等比缩放而不是扭曲:
E b = ∑ i ∑ j ∈ N ( i ) ∥ ( v i − v j ) × e i j ∥ 2 2 (9) E_{b} = \sum_{i} \sum_{j \in N(i)} \left \| (\mathbf{v}_i - \mathbf{v}_j) \times \mathbf{e}_{ij} \right \|_{2}^{2} \tag{9} Eb=i∑j∈N(i)∑∥(vi−vj)×eij∥22(9)
其中, e i j \mathbf{e}_{ij} eij 是沿着方向 p i − p j \mathbf{p}_i - \mathbf{p}_j pi−pj 的单位向量。 N ( i ) N(i) N(i) 表示网格点 i i i 的邻域
Regularization Term
最后,文章中引入了一个平滑的能量项,
E r = ∑ i ∑ j ∈ N ( i ) ∥ ( v i − v j ) ∥ 2 2 (10) E_{r} = \sum_{i} \sum_{j \in N(i)} \left \| (\mathbf{v}_i - \mathbf{v}_j) \right \|_{2}^{2} \tag{10} Er=i∑j∈N(i)∑∥(vi−vj)∥22(10)
Mesh Boundary Extension
文章中也提到,对于图像边缘的点,如果强制让其不移动的话,当人脸处于图像边缘的时候,会产生很明显的扭曲,为了解决这个问题,文章中采用网格扩展的方式,在原图的 mesh 基础上,往外扩展几个网格,同时让这些处于边界的网格点满足如下的约束:
{ v i , x = p i , x if p i ∈ left or right boundary v i , y = p i , y if p i ∈ top or bottom boundary (11) \begin{cases} v_{i,x} = p_{i,x} \quad \text{if} \quad \mathbf{p}_i \in \text{left or right boundary} \\ v_{i,y} = p_{i,y} \quad \text{if} \quad \mathbf{p}_i \in \text{top or bottom boundary} \\ \end{cases} \tag{11} {vi,x=pi,xifpi∈left or right boundaryvi,y=pi,yifpi∈top or bottom boundary(11)
这个约束保证了边界的点只会沿着边界移动,同时,为了减少 mesh warping 出现的未定义区域,文章中还利用了一个能量项,让原始 mesh 边缘的网格点尽量往外扩,而不是往内缩:
E a = E l + E r + E t + E b (12) E_a = E_l + E_r + E_t + E_b \tag{12} Ea=El+Er+Et+Eb(12)
{ E l = I ( v i , x > 0 ) ⋅ ∥ v i , x ∥ 2 2 , ∀ i ∈ ∂ l e f t E r = I ( v i , x < W ) ⋅ ∥ v i , x − W ∥ 2 2 , ∀ i ∈ ∂ r i g h t E t = I ( v i , y > 0 ) ⋅ ∥ v i , y ∥ 2 2 , ∀ i ∈ ∂ t o p E b = I ( v i , y < H ) ⋅ ∥ v i , y − H ∥ 2 2 , ∀ i ∈ ∂ b o t t o m (13) \begin{cases} E_l = \Bbb I(v_{i,x} > 0) \cdot \left \| v_{i,x} \right \|_{2}^{2}, \forall i\in \partial_{left} \\ E_r = \Bbb I(v_{i,x} < W) \cdot \left \| v_{i,x} -W \right \|_{2}^{2}, \forall i\in \partial_{right} \\ E_t = \Bbb I(v_{i,y} > 0) \cdot \left \| v_{i,y} \right \|_{2}^{2}, \forall i\in \partial_{top} \\ E_b = \Bbb I(v_{i,y} < H) \cdot \left \| v_{i,y} - H \right \|_{2}^{2}, \forall i\in \partial_{bottom} \\ \tag{13} \end{cases} ⎩ ⎨ ⎧El=I(vi,x>0)⋅∥vi,x∥22,∀i∈∂leftEr=I(vi,x<W)⋅∥vi,x−W∥22,∀i∈∂rightEt=I(vi,y>0)⋅∥vi,y∥22,∀i∈∂topEb=I(vi,y<H)⋅∥vi,y−H∥22,∀i∈∂bottom(13)
Optimization
最后的能量函数,就是将前面定义的能量函数加权:
E t = λ f E f + λ b E b + λ r E r + λ a E a (14) E_t = \lambda_{f}E_f + \lambda_{b}E_b + \lambda_{r}E_r + \lambda_{a}E_a \tag{14} Et=λfEf+λbEb+λrEr+λaEa(14)
对应权重分别设为:4,2,0.5,4
为了加速优化,文章在初始化的时候,也做了一些 trick:

最后 warp 的时候,文章中将优化得到的 mesh 还做了一个类似归一化的操作:
v n , i = s g ( v i ∗ + t g ) t g = − v 0 ∗ \mathbf{v}_{n, i} = s_g(\mathbf{v}_{i}^{*} + \mathbf{t}_g) \quad \mathbf{t}_g = -\mathbf{v}_{0}^{*} vn,i=sg(vi∗+tg)tg=−v0∗
最后的效果还是不错的,具体的样例可以看文章的 project 网站:
https://people.csail.mit.edu/yichangshih/wide_angle_portrait/
相关文章:

论文阅读:Distortion-Free Wide-Angle Portraits on Camera Phones
论文阅读:Distortion-Free Wide-Angle Portraits on Camera Phones 今天介绍一篇谷歌 2019 年的论文,是关于广角畸变校正的。 Abstract 广角摄影,可以带来不一样的摄影体验,因为广角的 FOV 更大,所以能将更多的内容…...

力扣每日一题---207. 课程表
Problem: 207. 课程表 文章目录 解题方法复杂度Code 解题方法 y总的 Topsort 模板题 复杂度 时间复杂度: 添加时间复杂度, 示例: O ( n ) O(n) O(n) 空间复杂度: 添加空间复杂度, 示例: O ( n ) O(n) O(n) Code class Solution {int res 0; public…...

在Kubernetes环境中有关Nginx Ingress与API Gateway的连接问题
文章目录 小结问题解决参考 小结 在Kubernetes环境中是通过Nginx Ingress来从外部访问Kubernetes内部的环境,并用API Gateway来分发请求,碰到了 502 Bad gateway.的问题,并尝试解决。 问题 从外部通过Nginx Ingress访问Kubernetes内部的环…...
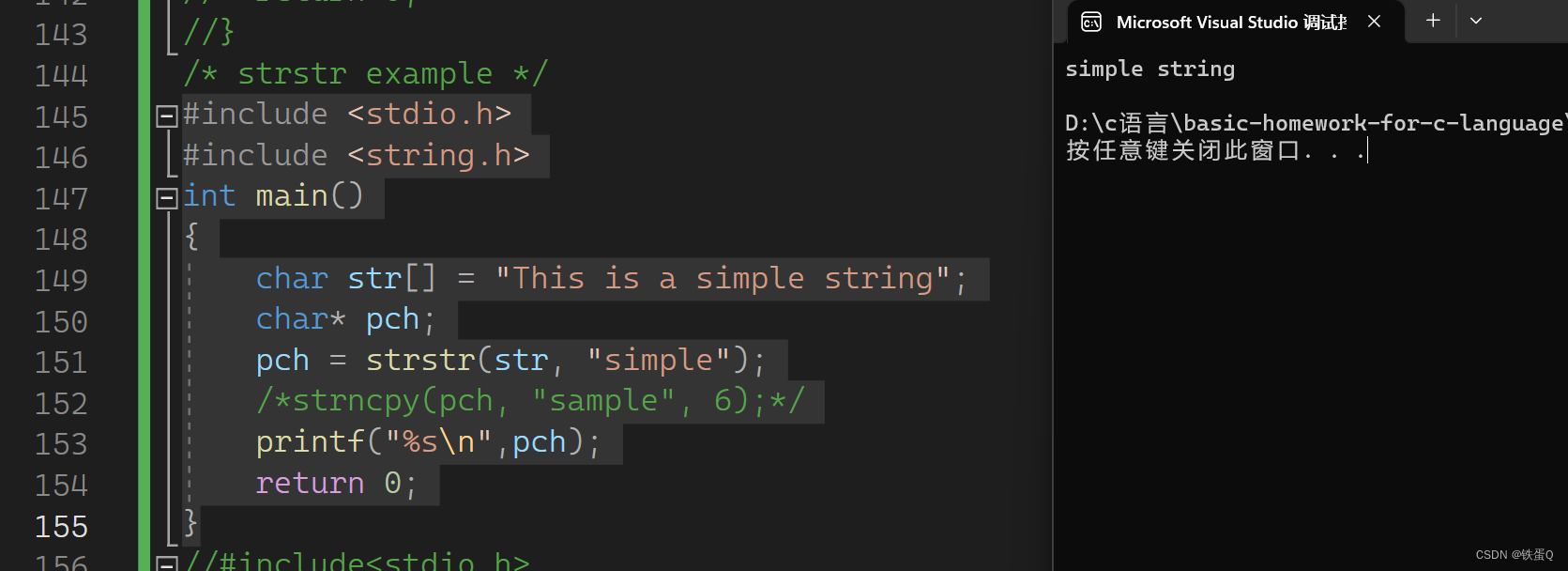
c语言练习44:深入理解strstr
深入理解strstr strstr作用展示: #include <stdio.h> #include <string.h> int main() {char str[] "This is a simple string";char* pch;pch strstr(str, "simple");/*strncpy(pch, "sample", 6);*/printf("%s…...
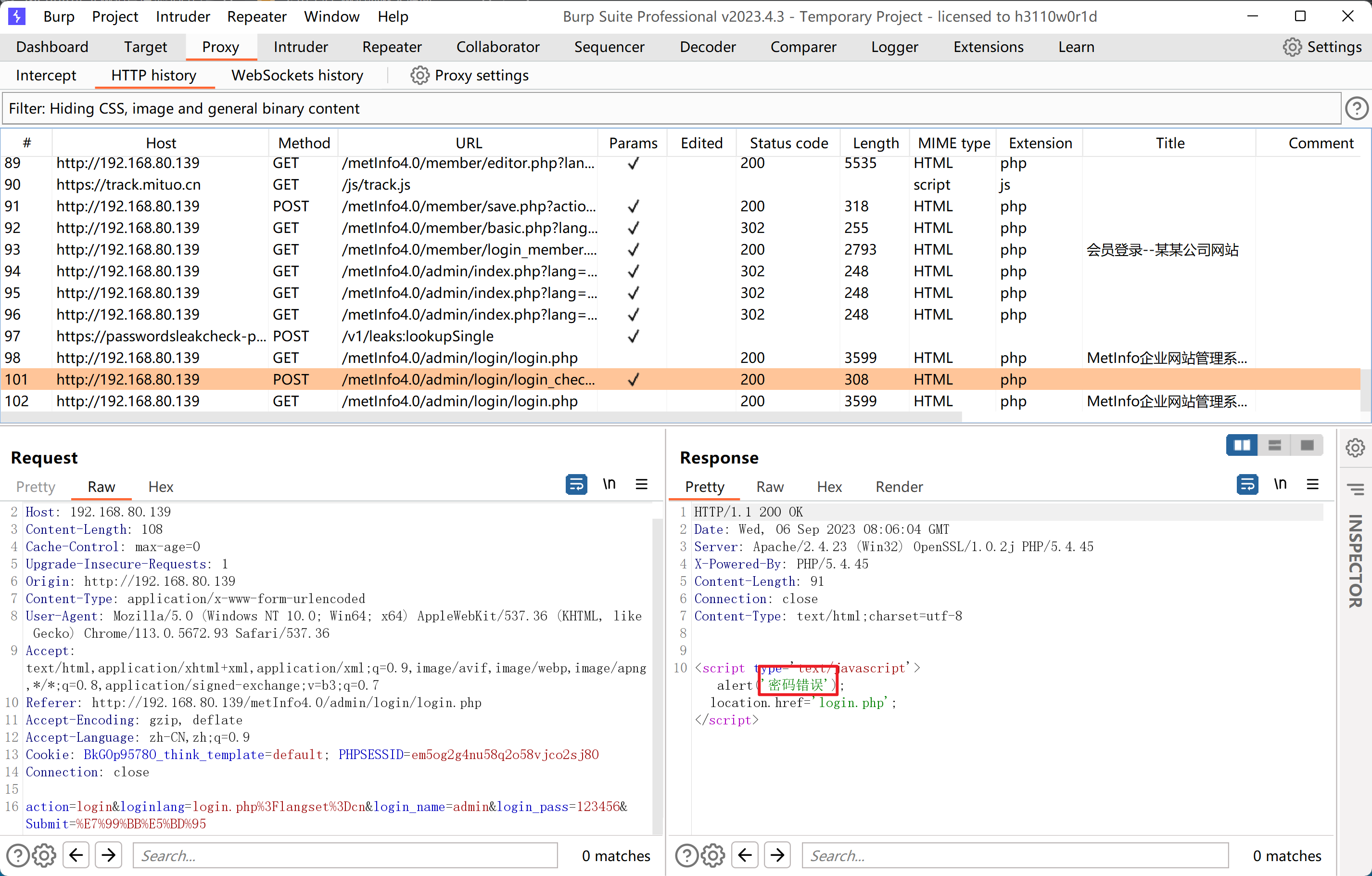
渗透测试漏洞原理之---【业务安全】
文章目录 1、业务安全概述1.1业务安全现状1.1.1、业务逻辑漏洞1.1.2、黑客攻击目标 2、业务安全测试2.1、业务安全测试流程2.1.1、测试准备2.1.2、业务调研2.1.3、业务建模2.1.4、业务流程梳理2.1.5、业务风险点识别2.1.6 开展测试2.1.7 撰写报告 3、业务安全经典场景3.1、业务…...

CentOS查看CPU、内存、网络流量和磁盘 I/O
安装 yum install -y sysstat sar -d 1 1 rrqm/s: 每秒进行 merge 的读操作数目。即 delta(rmerge)/s wrqm/s: 每秒进行 merge 的写操作数目。即 delta(wmerge)/s r/s: 每秒完成的读 I/O 设备次数。即 delta(rio)/s w/s: 每秒完成的写 I/O 设备次数。即 delta(wio)/s rsec/s:…...
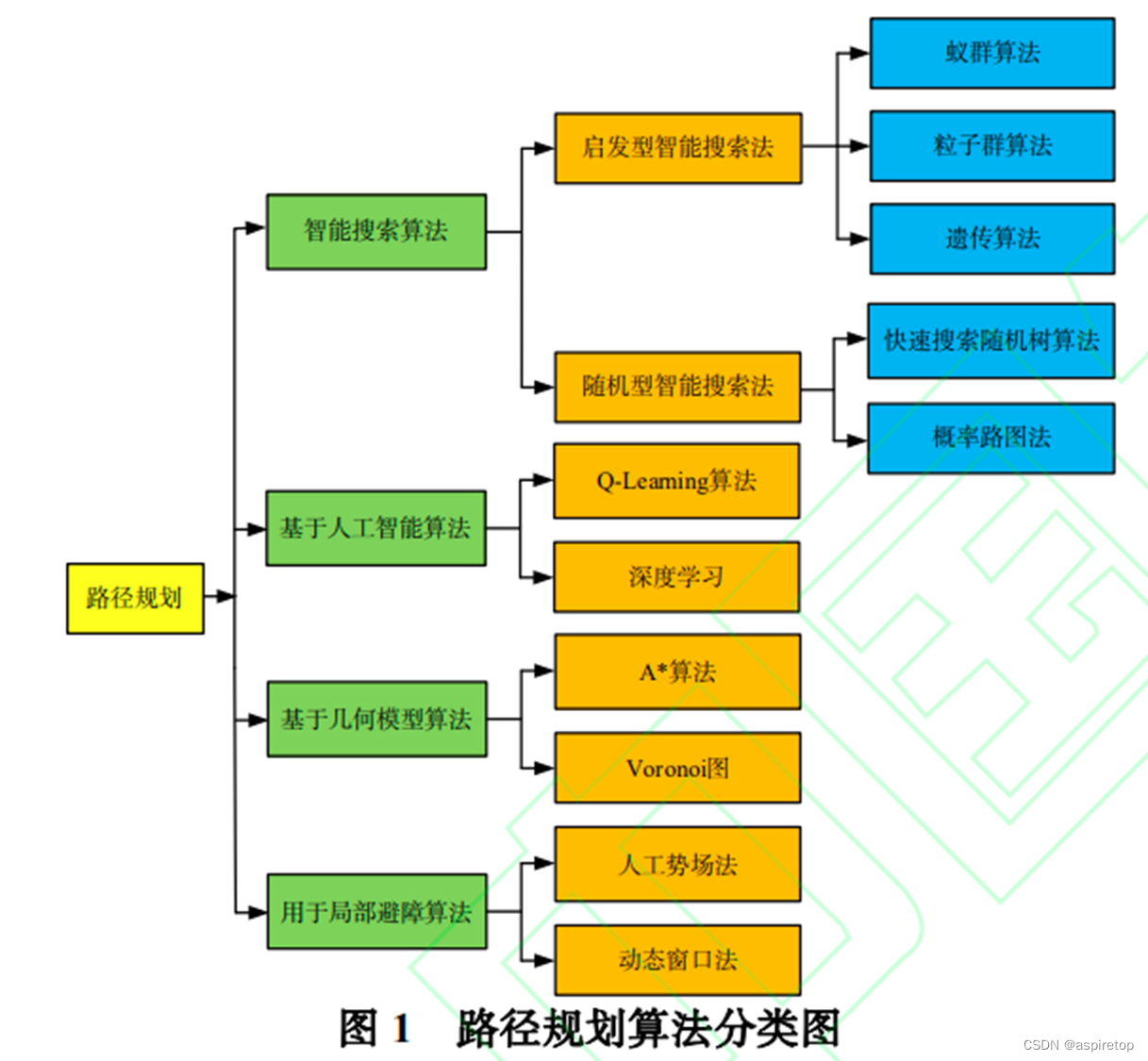
无人机航线规划
无人机航线规划,对于无人机的任务执行有着至关重要的作用,无人机在从起点飞向目的点的过程中,如何规划出一条安全路径,并且保证该路径代价最优,是无人机航线规划的主要目的。其中路径最优的含义是,在无人机…...

react中受控组件与非受控组件
受控组件与非受控组件 受控组件: 其值由 React 控制的组件,通常使用 state 来控制和修改组件的值。 例如受控的 组件: class NameForm extends React.Component {constructor(props) {super(props);this.state {value: };}handleChange (event) > {this.setState({val…...

【网络教程】如何解决Docker删除镜像和容器后磁盘空间未释放的问题
文章目录 问题分析解决方案删除未使用的容器删除未使用的镜像删除未使用的数据卷调整Docker数据存储路径问题分析 当删除Docker镜像和容器后,磁盘空间并未释放,这可能导致磁盘空间不足。造成此问题的原因包括: Docker镜像和容器的删除策略:默认情况下,Docker不会立即删除…...
Python中的进度条显示方案
迷途小书童 读完需要 3分钟 速读仅需 1 分钟 大家好,我是迷途小书童! tqdm 是一个非常常用的 Python 进度条库,它可以在循环迭代和 IO 操作期间添加一个进度条,直观地显示循环迭代的进程。 tqdm 是在 2013 年发布的,目的是为 Pyth…...

2023-09-05力扣每日一题
链接: 2605. 从两个数字数组里生成最小数字 题意: 两个数组都只包含1-9的数字,求一个最小数,两个数组内都要有它的其中一位 解: 要么是个位数要么是十位数,存一下数量和两边的最小数即可 实际代码&am…...

ODC现已开源:与开发者共创企业级的数据库协同开发工具
OceanBase 开发者中心(OceanBase Developer Center,以下简称 ODC)是一款开源的数据库开发和数据库管理协同工具,从首个版本上线距今已经发展了三年有余,ODC 逐步由一款专为 OceanBase 打造的开发者工具演进成为支持多数…...

生成克隆钓鱼网站与对win7进行后渗透操作
目录 目录 前言 系列文章列表 思维导图 1,实验涉及复现环境 2,CS的介绍 2.1,CS的简介 2.2,CS的主要功能 3,CS的安装 3.1,将cobalt_strike_4.5文件夹放到kali中 3.1,放入过程中的注意事项 3.2,如图所示 4,配置工具 4.1,进入c…...

Ubuntu18中NVIDIA,cuda,cudnn,pytorch安装
注意:nvidia驱动和cuda,cudnn,pytroch,python的对应关系 linux安装pytorch(包括cuda与cudnn)_linux清华园按照pytorch1.12_BryceRui的博客-CSDN博客 安装流程:安装cuda(包括nvidia驱动) cudnn python安装…...
MATLAB中M文件编写
简介 所谓M文件就是将处理问题的各种命令融合到一个文件中,该文件以.m为扩展名。然后,由MATLAB系统编译M文件,得出相应的运行结果。M文件具有相当大的可开发性和扩展性。M文件有脚本文件和函数文件两种。脚本文件不需要输入参数,…...
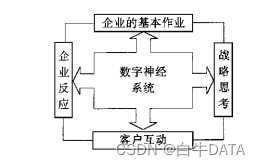
企业数字化神经网络
随着数字化时代的到来,数据已经成为企业战略性资源和重要的生产要素。企业数字化转型的核心是充分开发和利用数据资源,以数据为驱动,对业务流程进行重构与创新,从而提升企业的核心竞争力。业务系统是企业数据资源的源头࿰…...

C++this指针
本文旨在讲解C中this关键字,以及其相关作用! 定义 this 是 C 中的一个关键字,也是一个 const 指针,它指向当前对象,通过它可以访问当前对象的所有成员。 this的介绍 下面来看一下关于this这个关键字的实例࿰…...
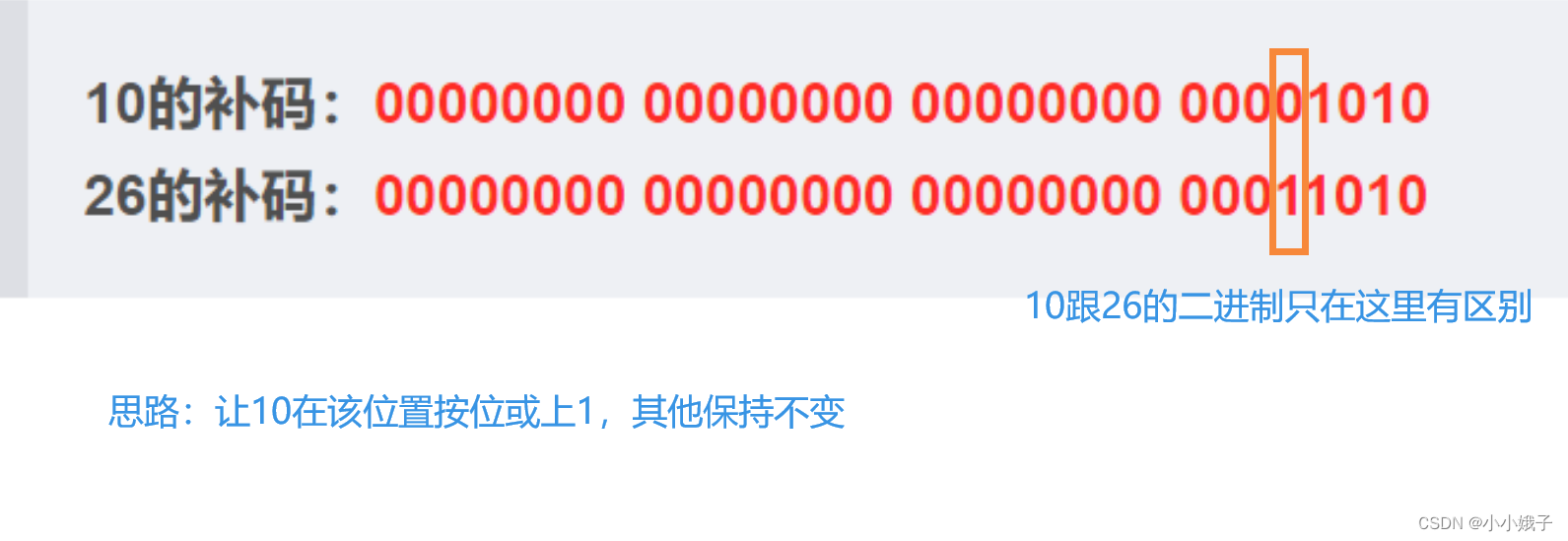
【初阶C语言】操作符1--对二进制的操作
前言:本节内容介绍的操作符,操作的对象是二进制位。所以前面先介绍整数的二进制位 一、二进制位介绍 1.二进制介绍 (1)整数的二进制表示形式有三种:原码、反码和补码。 (2)原码、反码和补码的…...

安装pyscipopt
安装pyscipopt Conda会自动安装SCIP,因此所有内容都可以通过单个命令安装: GitHub - scipopt/PySCIPOpt: Python interface for the SCIP Optimization Suite conda create --name myenv python3.8 # 创建新环境 conda activate myenv # 激活新环境 …...
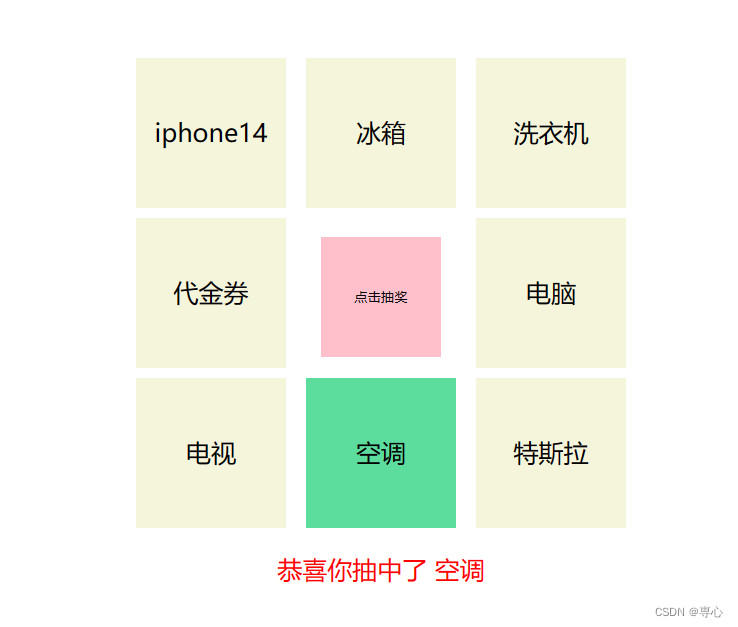
原生js实现的轮盘抽奖案例
来到大学也是有二年了,吃饭最多的地方就是在食堂,经过这么久的时间,已经几乎是把每个窗口的菜都吃腻了,所以我打算做个轮盘抽奖的形式来决定我每天要吃些什么。 目录 实现效果图: 静态搭建 js代码 1.实现此功能的思路…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
