物联网终端算法
物联网终端算法是指在物联网终端设备上运行的各种算法,包括数据采集、数据预处理、数据传输、数据存储、数据处理、数据分析等算法。以下是物联网终端算法的一些具体应用:
数据采集算法:用于采集各种传感器数据,包括温度、湿度、气压、光照、声音、震动等信息。
数据预处理算法:用于对采集到的数据进行去噪、滤波、校准等处理,提高数据质量。
数据传输算法:用于将终端采集到的数据传输到云端或其他终端设备,包括传统的WiFi、蓝牙、Zigbee、LoRa等通信方式,也包括新兴的NB-IoT、5G等通信技术。
数据存储算法:用于将采集到的数据存储到云端或本地存储设备中,包括关系型数据库、非关系型数据库、分布式存储系统等。
数据处理算法:用于对采集到的数据进行处理,包括数据转换、数据合并、数据聚类、数据分类等操作。
数据分析算法:用于对处理后的数据进行分析,提取有价值的信息,包括预测分析、异常检测、趋势分析、关联分析等。
综上所述,物联网终端算法是物联网的核心技术之一,其发展将进一步推动物联网技术的发展和应用。
相关文章:

物联网终端算法
物联网终端算法是指在物联网终端设备上运行的各种算法,包括数据采集、数据预处理、数据传输、数据存储、数据处理、数据分析等算法。以下是物联网终端算法的一些具体应用: 数据采集算法:用于采集各种传感器数据,包括温度、湿度、气…...

【面试刷题】——TCP三次握手,以及为什么要三次握手
TCP(传输控制协议)的三次握手是建立TCP连接的过程,它确保了通信双方的正常启动和参数协商。三次握手的过程如下: 客户端发送请求: 客户端首先向服务器发送一个特殊的TCP报文,称为SYN(同步&…...

算法系列-力扣206-单链表反转
题目说明 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 方法一:头插法反转链表 思路: 声明p指针指向原头节点,并将头节点置空;p指针循环原链表将元素用头节点插入法逐个插入head中&…...
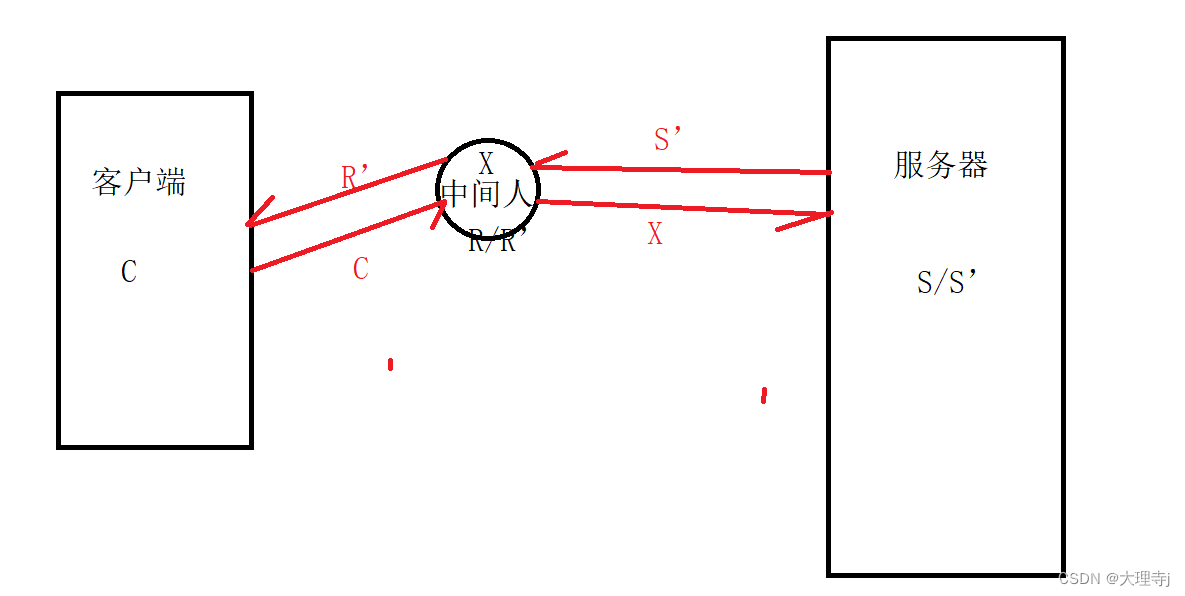
网络基础-应用层协议-HTTP/HTTPS
HTTP/HTTPS HTTP基本概念协议格式请求报文请求方法请求资源地址协议版本 应答报文 常见Header常见状态码与状态描述Cookie&Sessionhttp协议特点 HTTPS基本概念对称加密与非对称加密数据摘要&数据指纹HTTPS工作过程探究只采用对称加密只采用非对称加密双方都采用非对称加…...
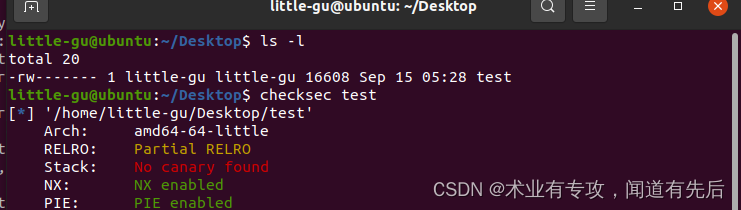
problen(5)ubuntu版本问题
浅浅记录一下这段时间的血和泪吧,大概耗时快一个月了吧,终于解决了...... 因为需要开启pwn之旅,需要在Ubuntu上安装一些东西,就是下面的一条命令: sudo pip3 install pwntools -i Simple Index(显示不太好了…...
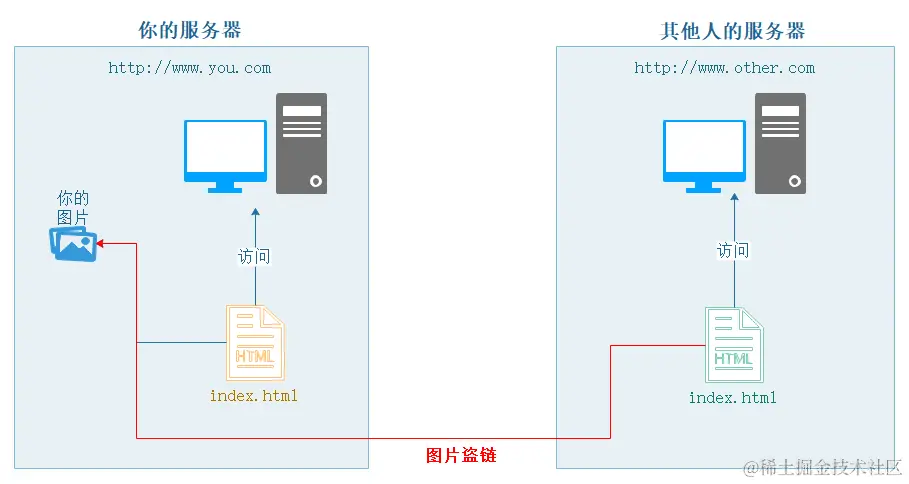
写一篇nginx配置指南
nginx.conf配置 找到Nginx的安装目录下的nginx.conf文件,该文件负责Nginx的基础功能配置。 配置文件概述 Nginx的主配置文件(conf/nginx.conf)按以下结构组织: 配置块功能描述全局块与Nginx运行相关的全局设置events块与网络连接有关的设置http块代理…...

rhel8防火墙firewalld操作
1.查看默认区域 [rootlocalhost r]# firewall-cmd --get-default-zone public2.查看网卡关联的区域 [rootlocalhost r]# firewall-cmd --get-zone-of-interfaceifcfg-ens160 external 3.设置网卡的默认区域修改为work [rootlocalhost r]# firewall-cmd --zonework --change…...

OpenCV项目实战(2)— 如何用OpenCV实现弹球动画
前言:Hello大家好,我是小哥谈。OpenCV能够在画布上绘制静态的图形,例如,线段、矩形、正方形、圆形、多边形、文字等。那么,能不能让这些静态的图形移动起来?如果能,又该如何编写代码呢ÿ…...

golang iris框架 + linux后端运行
go mod init myappgo get github.com/kataras/iris/v12latestpackage mainimport "github.com/kataras/iris/v12"func main(){app : iris.New()app.Listen(":port") }打包应用 go build main.go开启服务 #nohup ./程序名称 nohup ./main关闭后台 #ps -e…...

linux shell操作- 02 常用命令及案例
文章目录 常用命令 续 常用命令 续 定时任务 通过文本编辑cron任务,实现定时操作 分 小时 天 月 星期 绝对路径sh or cmd* 表示每个xxx,如每个小时每小时的第三分钟执行cmd-> 03 * * * * /home/lauf/scraw.sh每天的第5、8个小时执行-> 00 5,8 * *…...
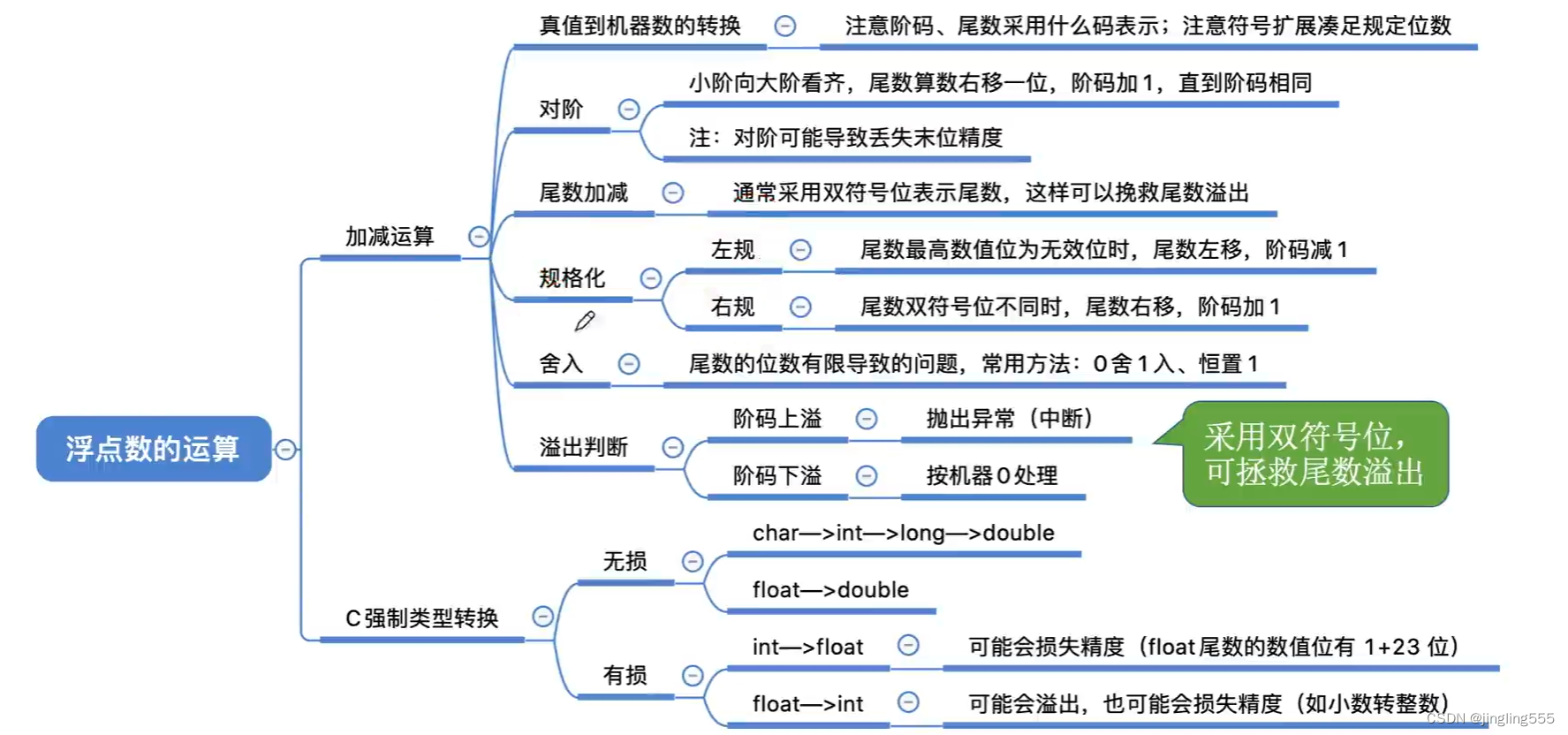
考研408 | 【计算机组成原理】 数据的表示和运算
进位计数制 十进制计数法: 推广:r进制计数法 任意进制-->十进制: 二进制<-->八进制、十六进制: 各种进制的常见书写方式: 十进制-->任意进制: 十进制-->二进制(拼凑法ÿ…...
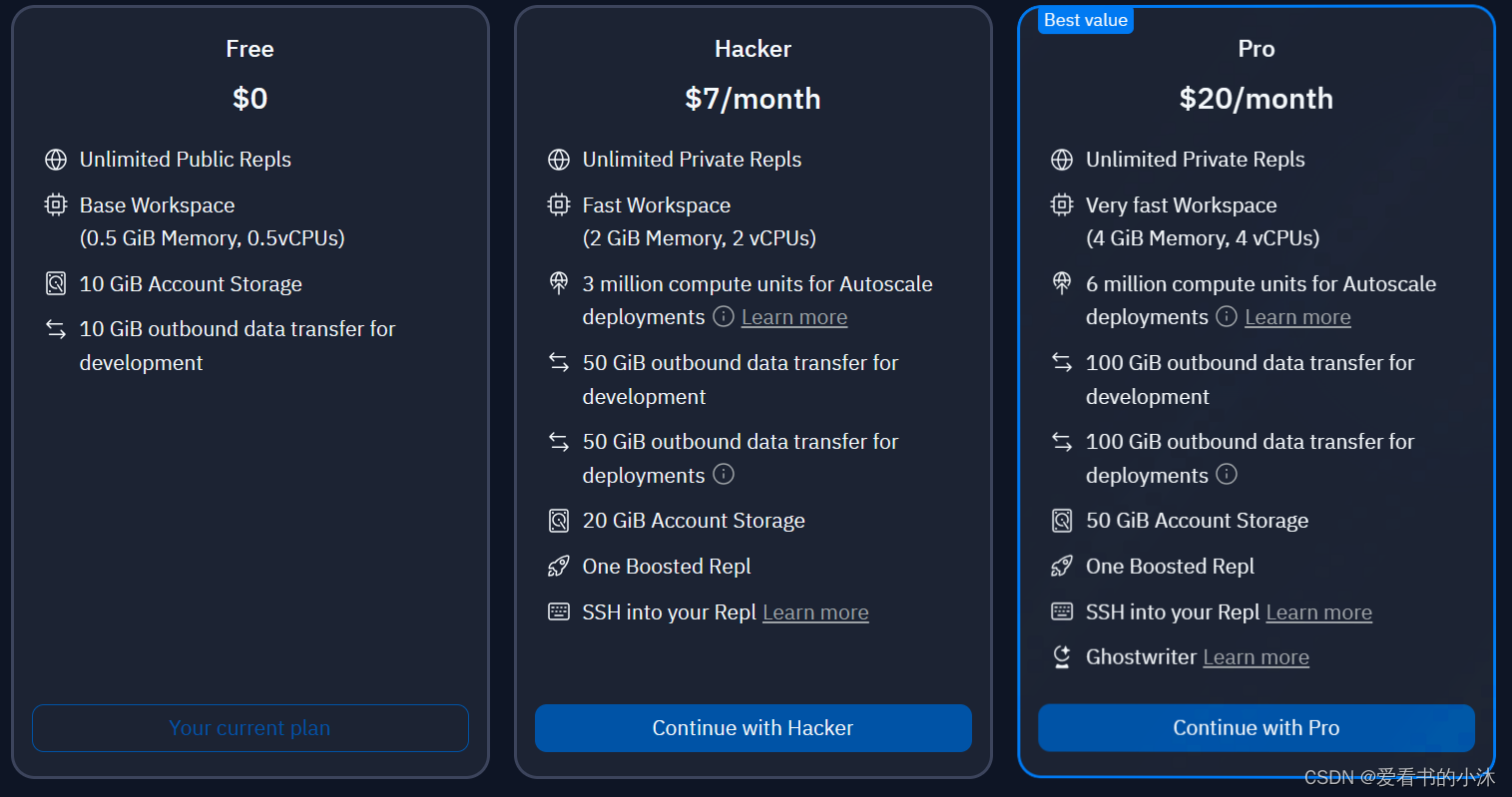
【小沐学NLP】AI辅助编程工具汇总
文章目录 1、简介2、国内2.1 aiXcoder2.1.1 工具特点2.1.2 部署方式2.1.3 使用费用2.1.4 代码测试2.1.4.1 代码搜索引擎2.1.4.2 在线体验 2.2 CodeGeeX2.2.1 工具特点2.2.2 部署方式2.2.3 使用费用2.2.4 代码测试 2.3 Alibaba Cloud AI Coding Assistant(cosy&#…...
)
linux动态扩容系统盘(非lvm磁盘)
查看磁盘状态 执行df -Th查看磁盘情况 [rootiotdbtest1 ~]# df -Th Filesystem Type Size Used Avail Use% Mounted on devtmpfs devtmpfs 7.7G 0 7.7G 0% /dev tmpfs tmpfs 7.7G 0 7.7G 0% /dev/shm tmpfs tmpfs …...

Gitlab仓库部署
Gitlab仓库部署 一、Gitlab的概述1、gitlab介绍2、gitlab主要功能3、gitlab和github的区别 二、部署环境1、安装依赖环境2、安装Postfix邮箱3、Gitlab优势4、Gitlab工作流程 三、Gitlab部署过程1、Yum安装Gitlab2、配置gitlab站点URL3、启动并访问Gitlab 四、Gitlab具体操作1、…...
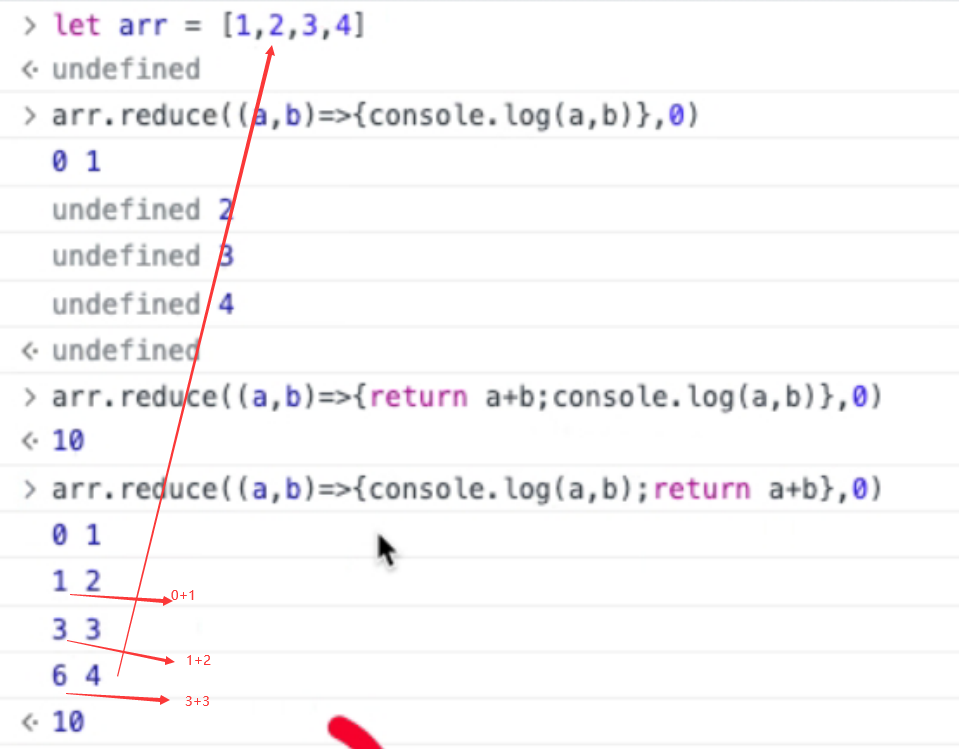
Day46:项目-购物车案例
购物车案例 准备工作 首页默认加载,其余页面懒加载 调用defineStore方法构建store 入口main做对应配置,找指南,快速开始,把elementplus引入进来 import { createApp } from "vue"; import { createPinia } from &qu…...
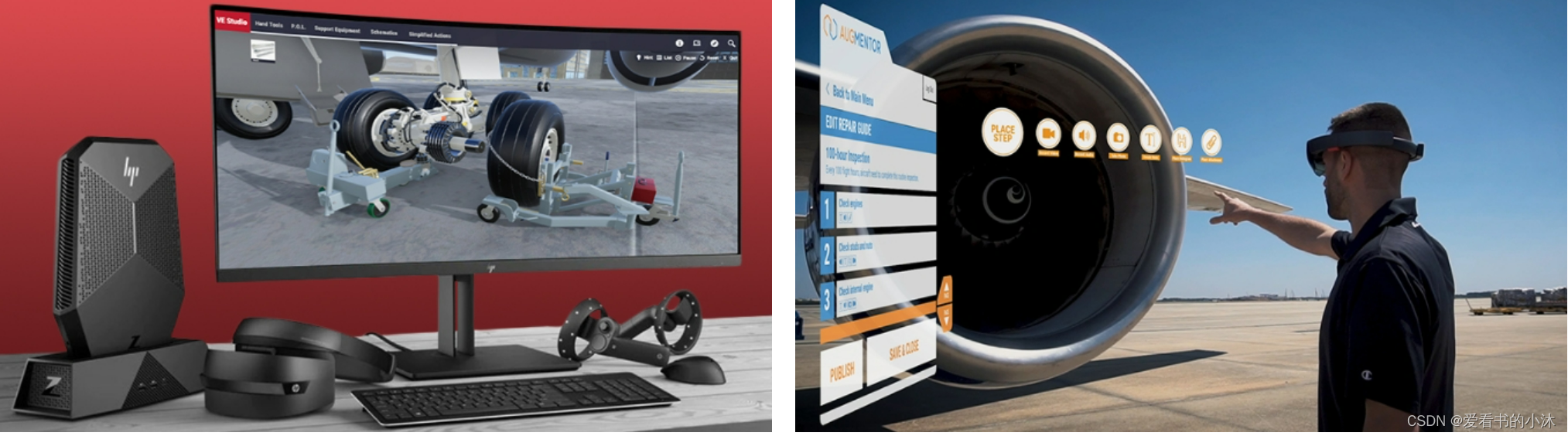
【小沐学CAD】嵌入式UI开发工具:GL Studio
文章目录 1、简介2、软件功能3、应用行业3.1 航空3.2 汽车3.3 防御3.4 工业3.5 电力与能源3.6 医疗3.7 空间3.8 科技 结语 1、简介 https://disti.com/gl-studio/ DiSTI 是 HMI 软件、虚拟驾驶舱、仪表、信息娱乐、集群显示器和嵌入式 UI 解决方案的领先提供商。 而它的GL Stu…...
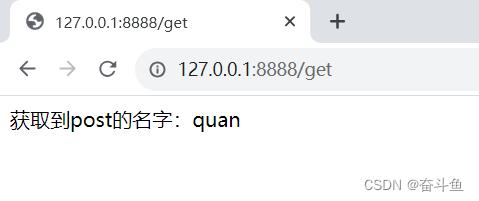
Python:Tornado框架之获取get和post的传参
一、获取get方式传参 import tornado.ioloop #导入tornado包 import tornado.web class MainHandle(tornado.web.RequestHandler):def get(self,id): #定义请求函数self.write("Hello %s!" %id)apptornado.web.Application([ #定义应用配置函数(r"/…...

JSON和全局异常处理
目录 1️⃣JSON 一、什么是json? 二、与javascript的关系 三、语法格式 四、注意事项 五、总结 六,使用json 1导入pom.xml依赖 2.配置spring-mvc.xml 3. ResponseBody注解使用 创建一个web层控制器 编写ClazzBiz 实现接口 测试: …...

骨传导耳机有害处吗、骨传导耳机真的不好用吗?
骨传导耳机没有害处。 骨传导耳机是通过将声音传递到颅骨,再由颅骨传递到内耳,从而达到听声音的效果,与传统的耳机不同。 因此,骨传导耳机不会直接对人的身体健康、耳朵产生压力和损伤,也不会影响耳道和中耳的正常功能…...

第一类曲面积分:曲面微元dσ与其投影面积微元dxdy之间的关系推导
第一类曲面积分:曲面微元dσ与其投影面积微元dxdy之间的关系推导 本篇博客精简自本人关于曲面积分的博客:详情见:曲面积分(Surface Integral) 曲面参数化(曲面上的每个点都使用起点为原点、终点为该曲面上的点的向量表示&#x…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
