【李沐深度学习笔记】数据操作实现
课程地址
数据操作实现p2
数据操作
首先导入PyTorch包(import torch),虽然叫PyTorch,但实际上要导入torch。
import torch
张量
张量表示的是一个数值组成的数组,这个数组可以有很多个维度。
# 生成0-11的顺序序列构成的一维数组张量(12那里是开区间,取不到)
x = torch.arange(12)
print(x)
输出结果:tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
张量的形状和元素个数
# 访问张量的形状(一维显示长度)
print(x.shape)
# 张量中元素的个数
print(x.numel())
输出结果:
torch.Size([12])
12
改变张量的形状
将上面的张量变为3X4的矩阵形式
print(x.reshape(3,4))
输出结果:
tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
全0和全1张量
# 定义1个3X4的张量,元素全为0
x = torch.zeros((3,4))
print(x)
# 定义1个2X3X4的张量,元素全为1
x = torch.ones((2,3,4))
print(x)
输出结果:
tensor([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
tensor([[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]],
[[1., 1., 1., 1.],[1., 1., 1., 1.],[1., 1., 1., 1.]]])
用Python的列表创建张量
# 用Python的列表创建张量(此处为2阶方阵)
x = torch.tensor([[1,2],[3,4]])
print(x)
# 打印其形状(维度)
print(x.shape)
输出结果:
tensor([[1, 2],
[3, 4]])
torch.Size([2, 2])
张量的常见运算
x1 = torch.tensor([1,1,1,3]) # 注意,张量的元素类型必须是相同的,假如这里面有浮点数,则所有元素都是浮点数
x2 = torch.tensor([0,2,0,6])
# 加法
x3 = x1 + x2
print(x3)
# 减法
x3 = x1 - x2
print(x3)
# 乘法
x3 = x1 * x2
print(x3)
# 除法
x3 = x2 / x1 # 0不能做分母
print(x3)
# 幂运算
x3 = x2 ** 2
print(x3)
# 指数函数e^x
x3 = torch.exp(x1)
print(x3)
# 开根号
x3 = torch.sqrt(x1)
print(x3)
运行结果:
tensor([1, 3, 1, 9])
tensor([ 1, -1, 1, -3])
tensor([ 0, 2, 0, 18])
tensor([0., 2., 0., 2.])
tensor([ 0, 4, 0, 36])
tensor([ 2.7183, 2.7183, 2.7183, 20.0855])
tensor([1.0000, 1.0000, 1.0000, 1.7321])
连结张量
# 按1到11的序列,并转换为3X4的矩阵,指定元素类型是32位浮点数
X = torch.arange(12, dtype=torch.float32).reshape(3,4)
Y = torch.tensor([[9,2,1,0],[3,1,0,2],[1,1,1,1]])
print("X=")
print(X)
print("Y=")
print(Y)
# 按行合并,dim参数设置为0
X1 = torch.cat((X,Y),dim=0)
print("dim=0:")
print(X1)
# 按列合并,dim参数设置为1
X1 = torch.cat((X,Y),dim=1)
print("dim=1:")
print(X1)
运行结果:
X=
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.]])
Y=
tensor([[9, 2, 1, 0],
[3, 1, 0, 2],
[1, 1, 1, 1]])
dim=0:
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[ 9., 2., 1., 0.],
[ 3., 1., 0., 2.],
[ 1., 1., 1., 1.]])
dim=1:
tensor([[ 0., 1., 2., 3., 9., 2., 1., 0.],
[ 4., 5., 6., 7., 3., 1., 0., 2.],
[ 8., 9., 10., 11., 1., 1., 1., 1.]])
通过逻辑运算符构建二维张量
- 判断两个维度和形状一致的张量是否相等,将对应位置元素是否相等的布尔值构建成一个元素全为布尔值的二维张量
a = torch.tensor([[1,2],[3,4]])
b = torch.tensor([[1,3],[2,4]])
print(a==b)
运行结果:
tensor([[ True, False],
[False, True]])
求和
# 对张量中所有元素求和,生成的是一个元素的张量(不是数字类型)
a = torch.tensor([[1,2],[3,4],[5,6]])
print(a.sum())
运行结果:
tensor(21)
广播机制
【问】什么是PyTorch的广播机制?
【chatGPT回答】在PyTorch中,广播机制是指在进行张量(Tensor)操作时,自动调整不同形状的张量,使它们能够按照一定规则进行元素级别的运算。
广播机制的主要目的是为了简化张量操作的代码编写过程,减少不必要的复制和内存消耗,并且增加代码的可读性。
当我们对两个形状不同的张量进行元素级别的运算时,广播机制会自动调整其中一个形状,使其与另一个张量的形状相匹配,从而使两个张量能够进行元素级别的运算。
具体来说,广播机制遵循以下规则:
- 如果两个张量的维度数不同,将较低维度的张量进行扩展,直到维度匹配。这通常是通过在维度较小的张量前面添加大小为1的维度来实现的。
- 如果两个张量在某个维度上的大小不一致,但其中一个张量的大小为1,那么可以通过复制该张量的数据来扩展其大小以匹配另一个张量。
- 如果两个张量在某个维度上的大小都不一致,并且都不为1,则不能进行广播,会引发形状不匹配的错误。
通过广播机制,我们可以方便地对不同形状的张量进行元素级别的运算,而不需要手动调整张量的形状。这种灵活性使得我们可以更加高效地进行各种张量操作,如加法、减法、乘法等,而无需显式地复制和扩展张量。
总之,PyTorch中的广播机制允许我们在处理不同形状的张量时,自动调整其形状,使其能够进行元素级别的运算,从而简化了张量操作的编写过程。
# 广播机制测试
a = torch.tensor([[1],[1],[0]])
b = torch.tensor([[1,2]])
print(a+b)
运行结果:
tensor([[2, 3],
[2, 3],
[1, 2]])
这里解释一下,由于a的列数与b的行数相等,所以可以将a的列数扩展复制成b的列数,将b的行数扩展复制成a的行数
a = [ 1 1 0 ] , b = [ 1 , 2 ] a = \begin{bmatrix}1 \\1 \\0 \end{bmatrix},b=[1,2] a= 110 ,b=[1,2],则按照广播机制,则将其扩展成:
a ∗ = [ 1 1 1 1 0 0 ] , b ∗ = [ 1 2 1 2 1 2 ] , ∴ a ∗ + b ∗ = [ 2 3 2 3 1 2 ] a_{*}=\begin{bmatrix} 1&1 \\ 1&1 \\0 &0 \end{bmatrix},b_{*}=\begin{bmatrix} 1&2 \\ 1&2 \\ 1&2 \end{bmatrix},\therefore a_{*}+b_{*}=\begin{bmatrix} 2&3 \\ 2&3 \\ 1&2 \end{bmatrix} a∗= 110110 ,b∗= 111222 ,∴a∗+b∗= 221332
倘若二者的行维度和列维度根本没有一个是相等的,则报错:
# 报错
a = torch.tensor([[1,2],[3,4]]) # 2*2
b = torch.tensor([[1,2,3],[4,5,6],[7,8,9]]) # 3*3
print(a+b)
报错结果:

元素访问
X = torch.tensor([[1,2,3],[4,5,6],[7,8,9],[10,11,12],[13,14,15],[16,17,18],[19,20,0]])
print(X)
# 访问最后一个元素(也就是[7,8,9]这个嵌套在里面的向量)
print(X[-1])
# 访问第2个到第4个元素(二维张量,每个元素是一个一维张量),左闭右开区间
print(X[1:4])
运行结果:
tensor([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12],
[13, 14, 15],
[16, 17, 18],
[19, 20, 0]])
tensor([19, 20, 0])
tensor([[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
写入张量
X = torch.tensor([[1,2,3],[4,5,6],[7,8,9],[10,11,12],[13,14,15],[16,17,18],[19,20,0]])
print(X)
# 访问第3行第2列(下标从0开始)
print(X[2,1])
# 修改第1行第3列元素的值
X[0,2] = 100
print(X)
运行结果:
tensor([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12],
[13, 14, 15],
[16, 17, 18],
[19, 20, 0]])
tensor(8)
tensor([[ 1, 2, 100],
[ 4, 5, 6],
[ 7, 8, 9],
[ 10, 11, 12],
[ 13, 14, 15],
[ 16, 17, 18],
[ 19, 20, 0]])
为多个元素赋相同的值
X = torch.tensor([[1,2,3],[4,5,6],[7,8,9],[10,11,12],[13,14,15],[16,17,18],[19,20,0]])
print(X)
# 给第2行到第5行中的第2列到第3列赋值(注意左闭右开)
X[1:6,1:3]=-1
print(X)
# 给第2行到第5行全赋值为-2,不管列,直接写成" : ",不管行也是同理
X[1:6,:]=-2
print(X)
运行结果:
tensor([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12],
[13, 14, 15],
[16, 17, 18],
[19, 20, 0]])
tensor([[ 1, 2, 3],
[ 4, -1, -1],
[ 7, -1, -1],
[10, -1, -1],
[13, -1, -1],
[16, -1, -1],
[19, 20, 0]])
tensor([[ 1, 2, 3],
[-2, -2, -2],
[-2, -2, -2],
[-2, -2, -2],
[-2, -2, -2],
[-2, -2, -2],
[19, 20, 0]])
运行一些操作可能会导致为新结果分配内存
- Python中id类似C语言中的指针,通过id的变化可以窥探内存是否分配
# 运行一些操作可能会导致为新结果分配内存
X = torch.ones(3,3)
Y = torch.zeros(3,3)
before = id(Y)
Y = X + Y
print(before == id(Y))
运行结果:
False
执行原地操作
- 直接用[:]赋值不会增加内存,是原地操作
X = torch.ones(3,3)
Y = torch.zeros(3,3)
print("id(X)="+str(id(X)))
X[:]=Y
print("id(X)="+str(id(X)))
运行结果:
id(X)=2411897114928
id(X)=2411897114928
可以看到id是一样的(虽然每个人运行的id可能不同)
说明变量X所占的内存区域是一样的
如果在后续计算中没有重复使用,我们也可以使用X[ : ] = X +Y或X+= Y来减少操作的内存开销。
X = torch.ones(3,3)
Y = torch.zeros(3,3)
before = id(X)
X[:] = X + Y
print(before == id(X))
运行结果:
True
转换为NumPy张量
# 将tensor转为numpy张量,再转回来
X = torch.ones(3,3)
A = X.numpy()
B = torch.tensor(A)
print(type(A))
print(type(B))
运行结果:
<class ‘numpy.ndarray’>
<class ‘torch.Tensor’>
将大小为1的张量转换为Python标量
# a是PyTorch中的张量
# a.item()对应的是numpy浮点数
# float(a)对应Python中的浮点数
# int(a)对应Python中的整数
a = torch.tensor([3.5])
print(a,a.item(),float(a),int(a))
运行结果:
tensor([3.5000]) 3.5 3.5 3
相关文章:

【李沐深度学习笔记】数据操作实现
课程地址 数据操作实现p2 数据操作 首先导入PyTorch包(import torch),虽然叫PyTorch,但实际上要导入torch。 import torch张量 张量表示的是一个数值组成的数组,这个数组可以有很多个维度。 # 生成0-11的顺序序列构成的一维…...
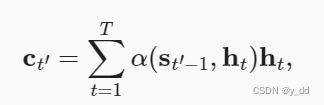
【深度学习-注意力机制attention 在seq2seq中应用】
注意力机制 为什么需要注意力机制attention机制的架构总体设计一、attention本身实现评分函数 attention在网络模型的应用-Bahdanau 注意力加性注意力代码实现 为什么需要注意力机制 这是一个普通的seq2seq结构,用以实现机器对话,Encoder需要把一个输入的…...

详解混合类型文件(Polyglot文件)的应用生成与检测
1. 引入 混合类型文件(Polyglot文件),是指一个文件,既可以是合法的A类型,也可以是合法的B类型。 比如参考3中的文件,是一个html文件,可以用浏览器正常打开;它也是一个一个.jar文件&…...

QT之QTableView的简介
QT之QTableView的简介 QTableView 是 Qt 框架中的一个类,用于显示和编辑表格数据。它提供了一个灵活的模型/视图架构,允许用户以不同的方式显示和编辑数据。 以下是 QTableView 的一些常用函数及其用法: 1)QTableView(QWidget *pa…...

学习记忆——宫殿篇——记忆宫殿——记忆桩——知识讲解
类比 假设这些桩子好比不同的交通工具,每一种交通工具都可以助我们到达目的地,那举现在就根据你的时间以及现实情况,选择最合适自己的交通工具即可,重点在于你要熟悉每种交通工具的用途不区别。桩子也是如此,把所有的桩…...

Python lambda匿名函数
视频版教程 Python3零基础7天入门实战视频教程 前面我们所学的函数定义,都是有函数名的。 我们现在学的lambda函数是没有名称的,也就是匿名函数。 我们在只需要一次性使用的函数的时候,就可以用lambda匿名函数,简单方便快捷。 …...
)
成绩统计(蓝桥杯)
成绩统计 题目描述 小蓝给学生们组织了一场考试,卷面总分为 100 分,每个学生的得分都是一个 0 到 100 的整数。 如果得分至少是 60 分,则称为及格。如果得分至少为 85 分,则称为优秀。 请计算及格率和优秀率,用百分数…...
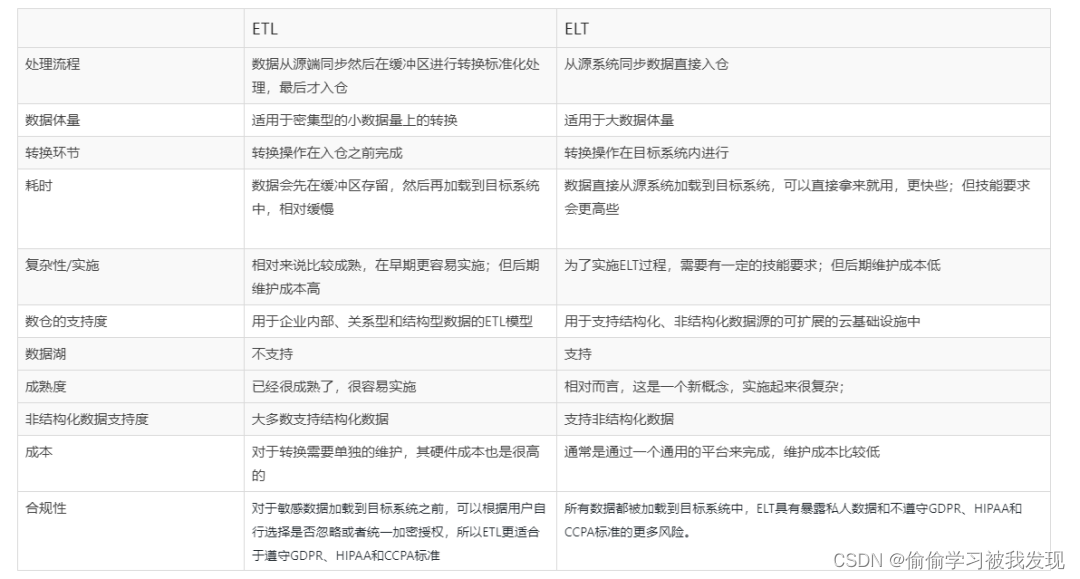
ETL与ELT理解
ETL ETL( Extract-Transform-Load),用来描述将数据从来源端经过抽取(Extract)、转换(Transform)、加载(Load)至目的端的过程。ETL模式适用于小数据量集。如果在转换过程…...
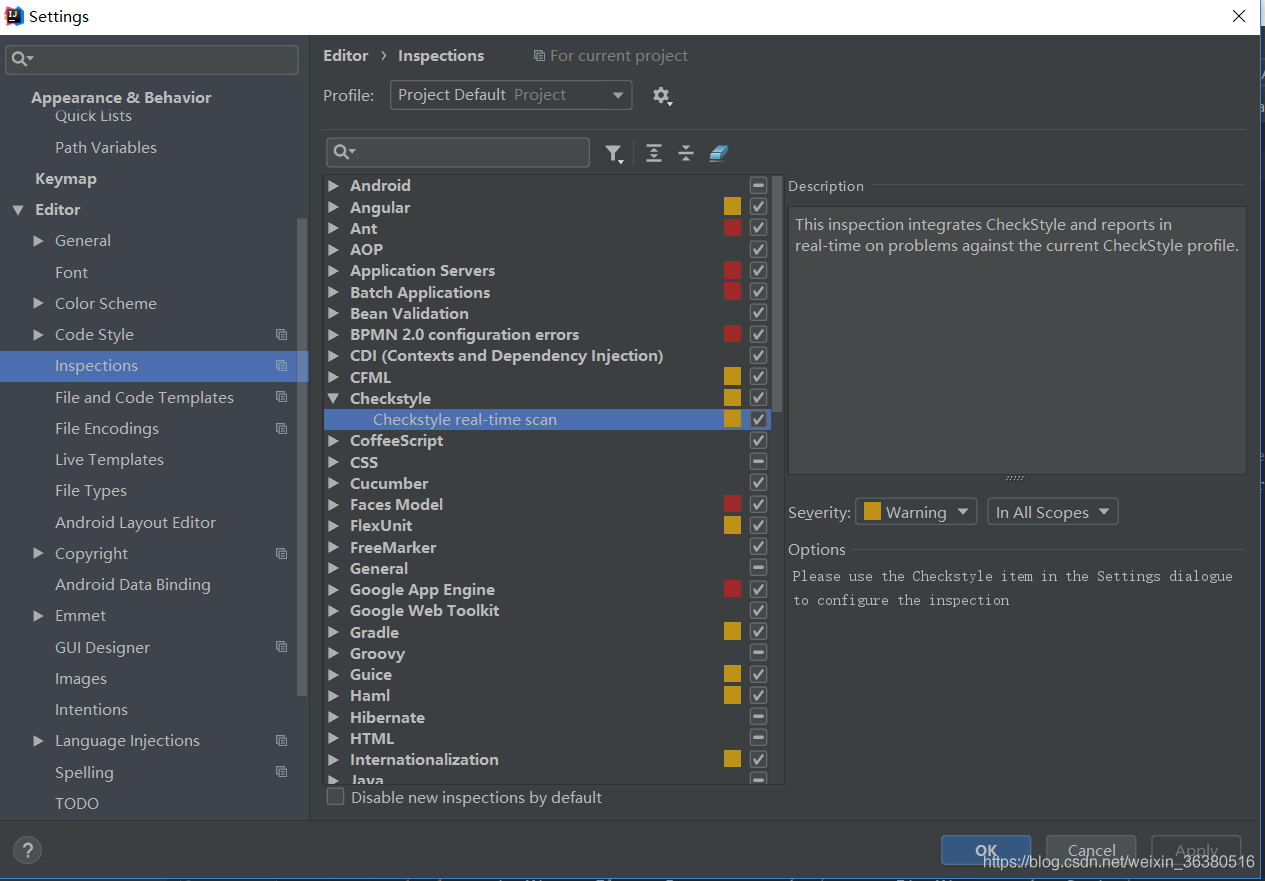
IntelliJ IDEA 2023 年下载、安装教程、好用插件推荐
文章目录 下载与安装IDEA常用插件推荐Alibaba Java Coding Guidelines(阿里巴巴Java开发规约)Key Promoter X(IDEA快捷键提示)Translation(翻译插件)Save Actions(优化保存插件)Codo…...

下载HTMLTestRunner并修改
目录 一. 下载HTMLTestRunner 二. 修改HTMLTestRunner 1. 修改内容 2. 修改原因 一. 下载HTMLTestRunner 下载报告模板地址:http://tungwaiyip.info/software/HTMLTestRunner.html 下载模块: 二. 修改HTMLTestRunner 将修改后的模块放到python安装目录下的..…...
C#回调函数学习1
回调函数(Callback Function)是一种函数指针,它指向的是由用户自己定义的回调函数。我们将这个回调函数的指针作为参数传递给另外一个函数,在这个函数工作完成后,它将通过这个回调函数的指针来回调通知调用者处理结果。…...

leetcode 232 用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty): 实现 MyQueue 类: void push(int x) 将元素 x 推到队列的末尾int pop() 从队列的开头移除并返回元素int peek() 返回队列开头…...

element UI表单验证,自定义验证规则
validator 可以为指定字段自定义验证函数——这就相当于把前边配置的东西用js按照以前的方式编写验证逻辑了。虽然麻烦点,但是能实现比较复杂的业务逻辑判断。 <el-form-itemlabel"中奖概率"prop"rate":rules"[{ required: true, mes…...

redis 主存复制
1. 前言 Redis的持久化机制,它很好的解决了单台Redis服务器由于意外情况导致Redis服务器进程退出或者Redis服务器宕机而造成的数据丢失问题。 在一定程度上保证了数据的安全性,即便是服务器宕机的情况下,也可以保证数据的丢失非常少。 通常…...

Unity Shader顶点数据疑问
1)Unity Shader顶点数据疑问 2)Unity 2018发布在iOS 16.3偶尔出现画面不动的问题 3)安卓游戏启动后提示“应用程序异常” 这是第352篇UWA技术知识分享的推送,精选了UWA社区的热门话题,涵盖了UWA问答、社区帖子等技术知…...
java写一个用于生成雪花id的工具类
我们创建一个类 叫 SnowflakeIdGenerator 作为生成雪花id的工具类 然后 编写代码如下 public class SnowflakeIdGenerator {private static final long START_TIMESTAMP 1609459200000L; // 设置起始时间戳,可以根据需要进行调整private static final long WORKER…...
淘宝开店装修教程 (2023新版)
一、下载千牛 1. 浏览器打开淘宝 https://www.taobao.com/ 2. 进入 - 千牛卖家中心 3. 进入 - 关于千牛 4. 下载千牛 5. 下载页面 6. 下载安装桌面 二、登录千牛 1. 登录页面 2. 进入 - 千牛工作台 三、pc店铺装修 1. 进入 - pc店铺 2. 进入 - 装修页面 3. 删除没用的模块 从…...
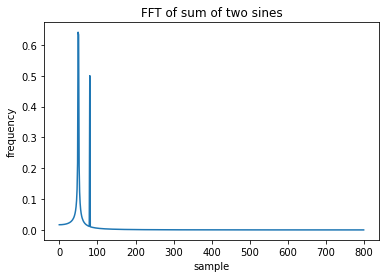
Python傅立叶变换
1. 什么是傅里叶变换? 在数学中,变换技术用于将函数映射到与其原始函数空间不同的函数空间。傅里叶变换时也是一种变换技术,它可以将函数从时域空间转换到频域空间。例如以音频波为例,傅里叶变换可以根据其音符的音量和频率来表示…...

MATLAB向量化编程基础精讲教程
向量化编程是MATLAB中一种重要的编程技术,通过使用向量和矩阵运算代替循环,可以提高代码的执行效率和可读性。本文将介绍MATLAB向量化编程的基础知识,并提供多个案例代码,帮助读者理解和应用向量化编程。 一、向量化编程基础知识…...

【非对称加密算法】RSA算法
一、非对称加密算法 非对称加密算法使用了两个不同的密钥:公钥和私钥。公钥是公开的,可以被任何人使用,而私钥是只有特定的人能够使用的。这种算法的加密和解密过程使用不同的密钥,因此称为非对称加密算法。 在非对称加密算法中…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...
