day-50 代码随想录算法训练营(19)动态规划 part 11
123.买卖股票的最佳时机|||
分析:只能买卖两次,就是说有五个状态:
- 没有买过
- 第一次买入
- 第一次卖出
- 第二次买入
- 第二次卖出
思路:二维数组,记录五个状态
- 1.dp存储:dp[i][1] 第一次买入 dp[i][2] 第一次卖出 dp[i][3] 第二次买入 dp[i][4] 第二次卖出
- 2.dp[i][1]=max(dp[i-1][1],dp[i-1][0]-prices[i])
- dp[i][2]=max(dp[i-1][2],dp[i-1][1]+prices[i])
- dp[i][3]=max(dp[i-1][3],dp[i-1][2]-prices[i])
- dp[i][4]=max(dp[i-1][4],dp[i-1][3]+prices[i])
- 3.初始化:dp[0][1]=-prices[0] dp[0][3]=-prices[0]
- 4.遍历顺序:1~n
class Solution {
public:int maxProfit(vector<int>& prices) {int n=prices.size();vector<vector<int>> dp(n,vector<int>(5,0));dp[0][1]=-prices[0];dp[0][3]=-prices[0];for(int i=1;i<n;i++){dp[i][0]=dp[i-1][0];//第一天不持有dp[i][1]=max(dp[i-1][1],dp[i-1][0]-prices[i]);dp[i][2]=max(dp[i-1][2],dp[i-1][1]+prices[i]);dp[i][3]=max(dp[i-1][3],dp[i-1][2]-prices[i]);dp[i][4]=max(dp[i-1][4],dp[i-1][3]+prices[i]);}return dp[n-1][4];}
};188.买卖股票的最佳时机IV
分析:买卖几次成了变量
思路:
- 1.dp存储:2k+1个状态的买卖金额
- 2.动态转移方程(递推式):
- j奇数:dp[i][j]=max(dp[i-1][j],dp[i-1][j-1]-prices[i])
- j偶数:dp[i][j]=max(dp[i-1][j],dp[i-1][j-1]+prices[i])
- 3.初始化:j奇数:dp[i][j]=-prices[0]
- 4.遍历顺序:1-n
class Solution {
public:int maxProfit(int k, vector<int>& prices) {int n=prices.size();int m=k*2;vector<vector<int>>dp(n,vector<int>(m+1,0));for(int i=1;i<=m;i+=2) dp[0][i]=-prices[0]; //初始化for(int i=1;i<n;i++){dp[i][0]=dp[i-1][0];//第一天不持有for(int j=1;j<m+1;j++){if(j%2!=0) dp[i][j]=max(dp[i-1][j],dp[i-1][j-1]-prices[i]);//第j天持有else dp[i][j]=max(dp[i-1][j],dp[i-1][j-1]+prices[i]);//第j天卖出}}return dp[n-1][m];}
};309.买卖股票的最佳时机含冷冻期
分析:现在有四种状态:买入股票 冷冻期后没买入 卖出股票 冷冻期
思路:dp存储四种状态
- 1.dp存储:四种状态
- 2.动态转移方程(递推式):
- dp[i][0]=max(dp[i-1][0],max(dp[i-1][1]-prices[i],dp[i-1][3]-prices[i]))
- dp[i][1]=max(dp[i-1][1],dp[i-1][3])
- dp[i][2]=dp[i-1][0]+prices[i]
- dp[i][3]=dp[i-1][2]
- 3.初始化:dp[0][0]=-prices[0]
- 4.遍历顺序:1~n
class Solution {
public:int maxProfit(vector<int>& prices) {int n=prices.size();vector<vector<int>>dp(n,vector<int>(4,0));dp[0][0]=-prices[0];for(int i=1;i<n;i++){dp[i][0]=max(dp[i-1][0],max(dp[i-1][1]-prices[i],dp[i-1][3]-prices[i]));//持有dp[i][1]=max(dp[i-1][1],dp[i-1][3]);//冷冻期后面不持有dp[i][2]=dp[i-1][0]+prices[i];//卖出dp[i][3]=dp[i-1][2];//冷冻期}return max(dp[n-1][3],max(dp[n-1][1],dp[n-1][2]));//最大值一定不持有}
};相关文章:
动态规划 part 11)
day-50 代码随想录算法训练营(19)动态规划 part 11
123.买卖股票的最佳时机||| 分析:只能买卖两次,就是说有五个状态: 没有买过第一次买入第一次卖出第二次买入第二次卖出 思路:二维数组,记录五个状态 1.dp存储:dp[i][1] 第一次买入 dp[i][2] 第一次卖…...

自定义权限指令与防止连点指令
1.权限指令 // 注册一个全局自定义权限指令 v-permission Vue.directive(permission, {inserted: function(el, binding, vnode) {const {value} binding; // 指令传的值// user:edit:phone,sysData:sampleconst permissions [user:edit:address, sysData:entrust, sysData:…...
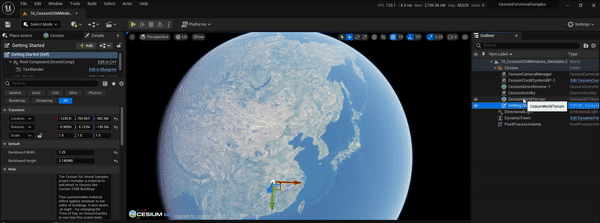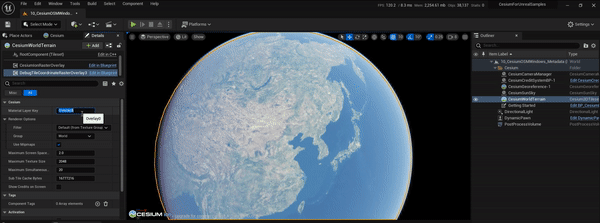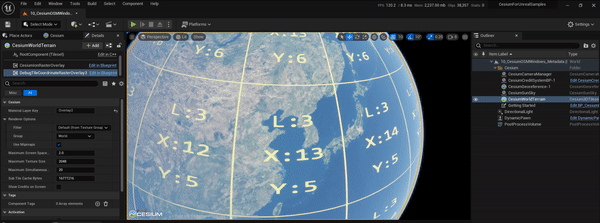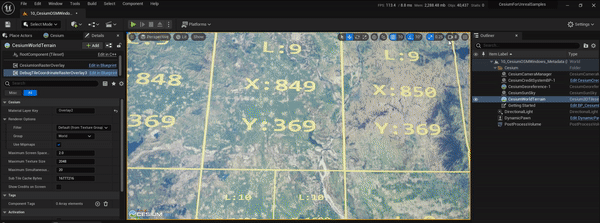
UE5、CesiumForUnreal实现瓦片坐标信息图层效果
文章目录 1.实现目标2.实现过程2.1 原理简介2.2 cesium-native改造2.3 CesiumForUnreal改造2.4 运行测试3.参考资料1.实现目标 参考CesiumJs的TileCoordinatesImageryProvider,在CesiumForUnreal中也实现瓦片坐标信息图层的效果,便于后面在调试地形和影像瓦片的加载调度等过…...

PostgreSQL执行计划
1. EXPLAIN命令 1)PostgreSQL中EXPLAIN命令的语法格式: postgres# \h explain Command: EXPLAIN Description: show the execution plan of a statement Syntax: EXPLAIN [ ( option [, ...] ) ] statement EXPLAIN [ ANALYZE ] [ VERBOSE ] statementwhere option can be…...

【2023 睿思芯科 笔试题】~ 题目及参考答案
文章目录 1. 题目 & 答案单选题编程题问题1:解析1:问题2:解析2: 声明 名称如标题所示,希望大家正确食用(点赞转发评论) 本次笔试题以两种形式考察的,分别是:选择题&a…...

Java手写AVL树
Java手写AVL树 1. AVL树实现思路原理 为了解释AVL树的实现思路原理,下面使用Mermanid代码表示该算法的思维导图: #mermaid-svg-ycH8kKpzVk2HWEby {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid…...

运维自动化:提高效率的秘诀
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...
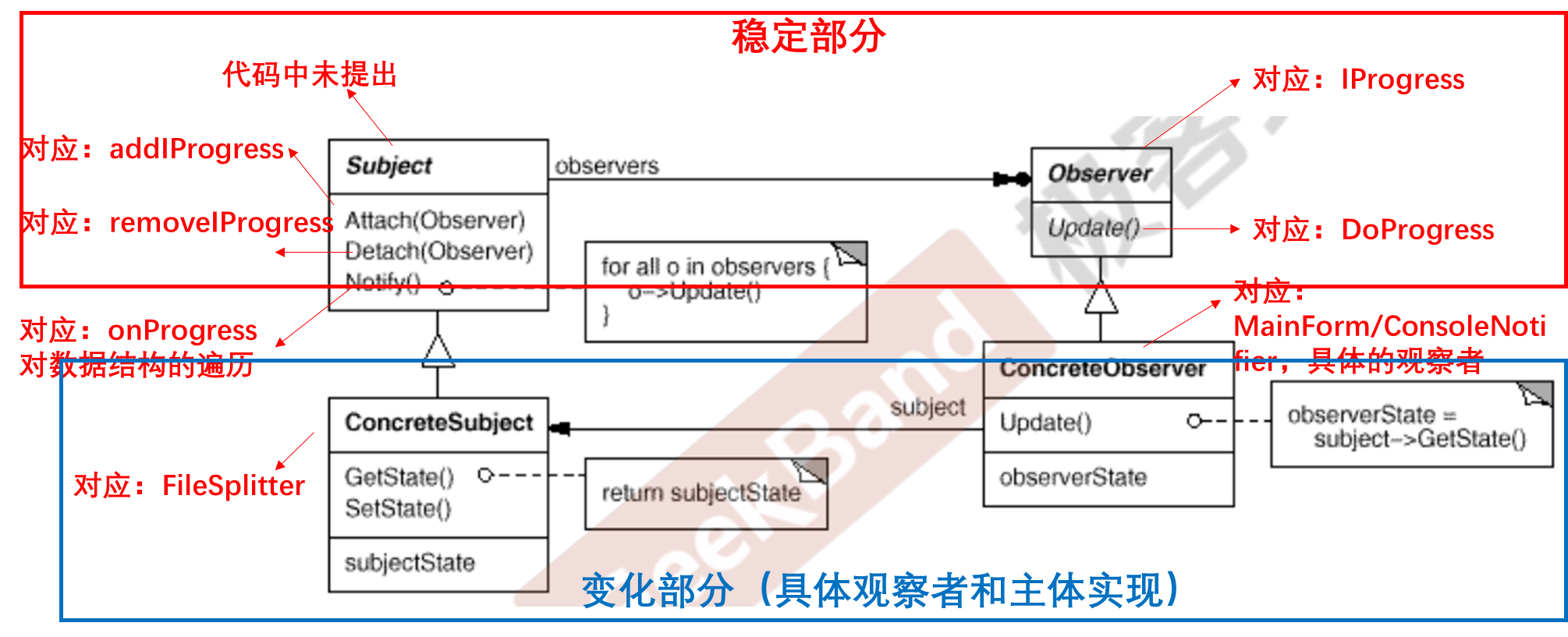
C++设计模式_05_Observer 观察者模式
接上篇,本篇将会介绍C设计模式中的Observer 观察者模式,和前2篇模板方法Template Method及Strategy 策略模式一样,仍属于“组件协作”模式。Observer 在某些领域也叫做 Event 。 文章目录 1. 动机( Motivation)2. 代码…...

github网站打不开,hosts文件配置
首先获取github官网的ip地址, 打开cmd,输入ping github.com 配置: #github 140.82.114.4 github.com 199.232.69.194 github.global.ssl.fastly.net 185.199.108.153 assets-cdn.github.com 185.199.110.153 assets-cdn.github.com 185.199…...

总结PCB设计的经验
一般PCB基本设计流程如下:前期准备->PCB结构设计->PCB布局->布线->布线优化和丝印->网络和DRC检查和结构检查->制版。: : 第一:前期准备。这包括准备元件库和原理图。“工欲善其事,必先利其器”,要做出一…...
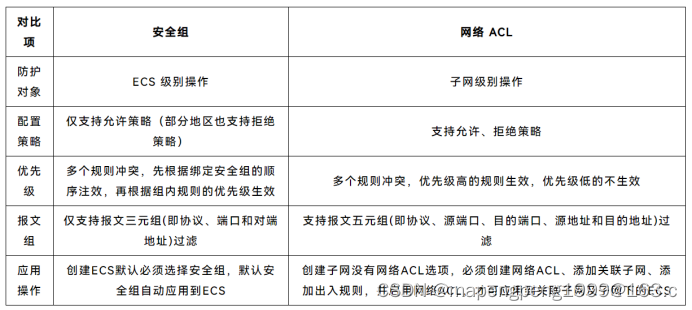
HCIE-HCS规划设计搭建
1、相关术语 1、等价路由 等价路由(Equal-cost routing)是一种网络路由策略,用于在网络中选择多个具有相同路由度量(路由距离或成本)的最佳路径之一来转发数据流量。 当存在多个路径具有相同的路由度量时,…...

c语言输出杨辉三角
#include<stdio.h> int main() {int x 0; //表示杨辉三角的的大小int y 1;printf("请输入x的值: ");scanf("%d", &x);for (int i 0; i < x; i) {for (int j 0; j < i; j) {if (j 0 || i 0) {y 1;}else {y y * (i - j 1) / j;}pri…...
)
性能测试-持续测试及性能测试建设(22)
什么是持续测试? 持续测试定义为:在软件交付流水线中执行自动化测试的过程,目的是获得关于预发布软件业务风险的即时反馈。 完成持续测试,我们还是需要回到定义中,它有3个关键词:软件交付流水线、自动化测试、即时反馈。 首先,持续测试需要具备一条完整的流水线,其代表…...

嵌入式C 语言中的三块技术难点
C 语言在嵌入式学习中是必备的知识,甚至大部分操作系统都要围绕 C 语言进行,而其中有三块技术难点,几乎是公认级别的“难啃的硬骨头”。 今天就来带你将这三块硬骨头细细拆解开来,一定让你看明白了。 0x01 指针 指针是公认…...

【斗破年番】紫研新形象,萧炎终成翻海印,救援月媚,三宗决战
Hello,小伙伴们,我是小郑继续为大家深度解析斗破年番。 斗破苍穹年番动画更新了,小医仙帅气回归,萧炎紫妍成功进入山谷闭关苦修,美杜莎女王守护没多久,就因蛇人族求救离开。从官方公布的最新预告来看,萧炎紫…...
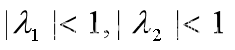
差分方程模型:国民总收入(GDP)的乘数-加速数模型
【背景知识-凯恩斯经济增长模型】 凯恩斯(John M.Keynes)建立了著名的国民经济增长模型。令Y表示国民总收入,C表示总消费,E为总支出,I表示投资,G为政府的投入(如基建等)。那么有 【6.1】 其中࿰…...

【C语言】指针和数组笔试题解析(1)
指针是C语言的灵魂,他的玩法多种多样,这篇文章带来指针的笔试题详解,可以帮助我们更好的理解与巩固指针的知识 目录 预备知识:题目:一维数组:二维数组: 题目比较多,但切记戒骄戒躁&a…...

Vue中组件的三种注册方式
组件的注册 1.全局注册: 在全局注册中,你需要确保在 Vue 根实例之前导入并注册组件。通常,你会在入口文件(例如 main.js)中执行这些操作。 // main.jsimport Vue from vue; import App from ./App.vue;// 导入全局组…...
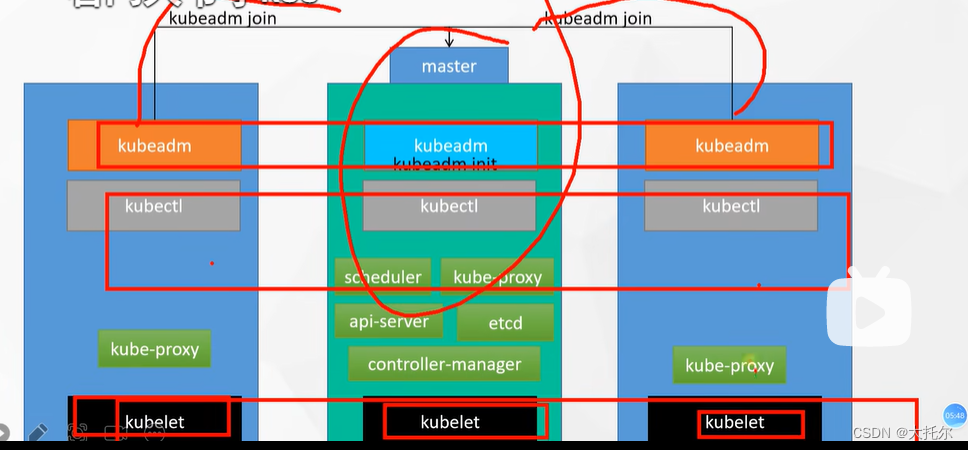
docker 和k8s 入门
docker 和k8s 入门 本文是云原生的学习记录,可以参考以下文档 k8s https://www.yuque.com/leifengyang/oncloud 相关视频教程可参考如下 https://www.bilibili.com/video/BV13Q4y1C7hS?p2&vd_source0882f549dac54045384d4a921596e234 相对于公有云&#x…...

基于Yolov8的交通标志牌(TT100K)识别检测系统
1.Yolov8介绍 Ultralytics YOLOv8是Ultralytics公司开发的YOLO目标检测和图像分割模型的最新版本。YOLOv8是一种尖端的、最先进的(SOTA)模型,它建立在先前YOLO成功基础上,并引入了新功能和改进,以进一步提升性能和灵活…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
