【八大经典排序算法】快速排序
【八大经典排序算法】快速排序
- 一、概述
- 二、思路实现
- 2.1 hoare版本
- 2.2 挖坑法
- 2.3 前后指针版本
- 三、优化
- 3.1 三数取中
- 3.1.1 最终代码
- 3.1.2 快速排序的特性总结
- 四、非递归实现快排

一、概述
说到快速排序就不得不提到它的创始人 hoare了。在20世纪50年代,计算机科学家们开始研究如何对数据进行排序,以提高计算机程序的效率。当时,常用的排序算法包括冒泡排序、插入排序和选择排序等。
然而,这些算法的效率都相对较低,特别是在处理大量数据时。于是,人们开始寻找更快速的排序算法。Tony Hoare 在研究中发现了一种基于分治思想的排序方法,即快速排序。
二、思路实现
快速排序的思想是任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
代码如下:
// 假设按照升序对array数组中[left, right]区间中的元素进行排序
void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;// 按照基准值对数组的 [left, right)区间中的元素进行划分int keyi = PartSort(a, begin, end);//分成[begin,keyi-1] keyi [keyi+1,end]// 递归排[left, div)QuickSort(a, begin, keyi - 1);// 递归排[div+1, right)QuickSort(a, keyi + 1, end);
}
上述为快速排序递归实现的主框架,发现与二叉树前序遍历规则非常像,接下来只需分析如何按照基准值来对区间中数据进行划分的方式即可。
待排序集合分割时,将区间按照基准值划分为左右两半部分的常见方式有以下3种。
2.1 hoare版本
思路:
- 选择一个基准元素(key),可以是最左边也可以是最右边。
- 定义两个指针,一个指向数组的第一个元素(左指针),一个指向数组的最后一个元素(右指针)。(需要注意的是:若选择最左边的数据作为key,则需要right先走;若选择最右边的数据作为key,则需要left先走)
- 移动左指针,直到找到一个大于等于基准元素(key)的元素;移动右指针,直到找到一个小于等于基准元素(key)的元素。之后交换交换左右指针所指向的元素。然后不断重复上述步骤直到左指针大于右指针
- 最后将基准元素与右指针所指向的元素交换位置,此时基准元素位于正确的位置。此时左边元素>=key,右边元素<=key。
Tips:博主在这里解释一下为什么“若选择最左边的数据作为key,则需要right先走;若选择最右边的数据作为key,则需要left先走”,后续其他方法同理。
① :左边作key,右边先走,保证了相遇位置的值小于key或就是key的位置。
②:右边作key,左边先走,保证了相遇位置的值大于key或就是key的位置。
以①为例,L和R相遇无非就两种情况:L遇R,R遇L。
情况一:L遇R。在R停下来后,L还在走。由于R先走,R停下来的位置一定小于Key。相遇位置为R停下来的位置,一定比key小。
情况二:R遇L。再相遇的这一轮,L就不动了,R在移动。相遇位置即为L的位置。而L的位置就是key的位置 or 已经交换过一些轮次了,此时相遇位置一定比key小。
【动画演示】:

代码如下:
//[left, right]--采用左闭右闭
int PartSort(int* a, int left, int right)
{int keyi = left;while (left < right){//找到右边比key小的数while (left < right && a[right] <= a[keyi]){right--;}//找到左边比key大的数while (left < right && a[left] >= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);return left;
}void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
2.2 挖坑法
思路:
- .选出一个数据(一般是最左边或是最右边的)存放在key变量中,同时该数据位置形成一个坑。
- 还是左右指针left和right,left从左向右走,right从右向左走。(若在最左边挖坑,则需要R先走;若在最右边挖坑,则需要L先走)
- 移动右指针找到第一个比key小的数并填到坑位,此时右指针所在位置变成新的坑。然后移动左指针找到第一个比key大的数并填到坑位,此时左指针所在位置变成新的坑。然后和hoare版本一样,不断重复上述步骤即可
【动画演示】:

代码如下:
//挖坑法
int PartSort(int* a, int left, int right)
{int key = a[left];int hole = left;while (left < right){//找到右边比key小的值while (left < right && a[right] >= key){right--;}a[hole] = a[right];hole = right;//左边比key大的值while (left < right && a[left] <= key){left++;}a[hole] = a[left];hole = left;}a[hole] = key;return hole;
}void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
2.3 前后指针版本
思路:
- 选出一个key,一般是最左边或是最右边的。
- 起始时,prev指针指向序列开头,cur指针指向prev+1。
- 若cur指向的内容小于key,则prev先向后移动一位,然后交换prev和cur指针指向的内容,然后cur指针++;若cur指向的内容大于key,则cur指针直接++。如此进行下去,直到cur到达end位置,此时将key和++prev指针指向的内容交换即可。
【动画演示】:

代码如下:
//前后指针法
int PartSort(int* a, int left, int right)
{int keyi = left;int prev = left;int cur = left + 1;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}cur++;}Swap(&a[prev], &a[keyi]);keyi = prev;return keyi;
}void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
三、优化
虽然已经可以解决问题了,但还有一个问题:
当选取的key每次都是中位数时,效率最好,时间复杂度为O(N*logN);但当数组有序时变成最坏,时间复杂度变为O(N^2)!
对于上述情况,这里有两种优化方式:
- 三数取中法选key
- 递归到小的子区间时,可以考虑使用插入排序
3.1 三数取中
这里博主给出一直最简单的方法:
int GetMidIndix(int* a, int left, int right)
{int mid = left + (right - left) / 2;if (a[left] < a[mid]){if (a[mid] < a[right])return mid;else if (a[mid] > a[right])return right;elsereturn left;}else//a[left]>=a[mid]{if (a[mid] > a[right])return mid;else if (a[mid] < a[right])return right;elsereturn left;}
}
3.1.1 最终代码
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}int GetMidIndix(int* a, int left, int right)
{int mid = left + (right - left) / 2;if (a[left] < a[mid]){if (a[mid] < a[right])return mid;else if (a[mid] > a[right])return right;elsereturn left;}else//a[left]>=a[mid]{if (a[mid] > a[right])return mid;else if (a[mid] < a[right])return right;elsereturn left;}
}// hoare
// [left, right]
//int PartSort(int* a, int left, int right)
//{
// int midi = GetMidIndix(a, left, right);
// Swap(&a[left], &a[midi]);
//
// int keyi = left;
// while (left < right)
// {
// //找到右边比key小的数
// while (left < right && a[right] <= a[keyi])
// {
// right--;
// }
//
// //找到左边比key大的数
// while (left < right && a[left] >= a[keyi])
// {
// left++;
// }
// Swap(&a[left], &a[right]);
// }
// Swap(&a[keyi], &a[left]);
// return left;
//}//挖坑法
//int PartSort(int* a, int left, int right)
//{
// int midi = GetMidIndix(a, left, right);
// Swap(&a[left], &a[midi]);
//
// int key = a[left];
// int hole = left;
// while (left < right)
// {
// //找到右边比key小的值
// while (left < right && a[right] >= key)
// {
// right--;
// }
// a[hole] = a[right];
// hole = right;
//
// //左边比key大的值
// while (left < right && a[left] <= key)
// {
// left++;
// }
// a[hole] = a[left];
// hole = left;
// }
// a[hole] = key;
// return hole;
//}//前后指针法
int PartSort(int* a, int left, int right)
{int midi = GetMidIndix(a, left, right);Swap(&a[left], &a[midi]);int keyi = left;int prev = left;int cur = left + 1;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}cur++;}Swap(&a[prev], &a[keyi]);keyi = prev;return keyi;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int keyi = PartSort(a, begin, end);//分成[begin,keyi-1] keyi [keyi+1,end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}
3.1.2 快速排序的特性总结
- 时间复杂度:O(N*logN)

- 空间复杂度:O(logN)
- 稳定性:不稳定
四、非递归实现快排
思路:
- 定义一个栈,然后将待排序的数组的起始索引和结束索引入栈。
- 通过前面将的三种分割区间的方法将数组的起始索引和结束索引之间的元素分成两部分,左边部分小于等于基准元素,右边部分大于等于基准元素。
- 由于非递归实现时,我们是通过从栈中两两取出维护待排序数组的下标,所以接下来就是如果左边部分的长度大于1,则将左边部分的起始索引和结束索引入栈;如果右边部分的长度大于1,则将右边部分的起始索引和结束索引入栈。最后循环此操作,直到栈为空。
代码如下:
//前后指针法
int PartSort(int* a, int left, int right)
{int midi = GetMidIndix(a, left, right);Swap(&a[left], &a[midi]);int keyi = left;int prev = left;int cur = left + 1;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}cur++;}Swap(&a[prev], &a[keyi]);keyi = prev;return keyi;
}//快排非递归
void QuickSortNonR(int* a, int begin, int end)
{ST st;STInit(&st);STPush(&st, end);STPush(&st, begin);while (!STEmpty(&st)){int left = STTop(&st);STPop(&st);int right = STTop(&st);STPop(&st);int keyi = PartSort(a, left, right);//[left,keyi-1] keyi [keyi+1,right]if (keyi + 1 < right){STPush(&st, right);STPush(&st, keyi + 1);}if (keyi - 1 > left){STPush(&st, keyi - 1);STPush(&st, left);}}STDestroy(&st);
}


相关文章:

【八大经典排序算法】快速排序
【八大经典排序算法】快速排序 一、概述二、思路实现2.1 hoare版本2.2 挖坑法2.3 前后指针版本 三、优化3.1 三数取中3.1.1 最终代码3.1.2 快速排序的特性总结 四、非递归实现快排 一、概述 说到快速排序就不得不提到它的创始人 hoare了。在20世纪50年代,计算机科学…...

vue 父组件给子组件传递一个函数,子组件调用父组件中的方法
vue 中父子组件通信,props的数据类型可以是 props: {title: String,likes: Number,isPublished: Boolean,commentIds: Array,author: Object,callback: Function,contactsPromise: Promise // or any other constructor }在父组件中,我们在子组件中给他…...
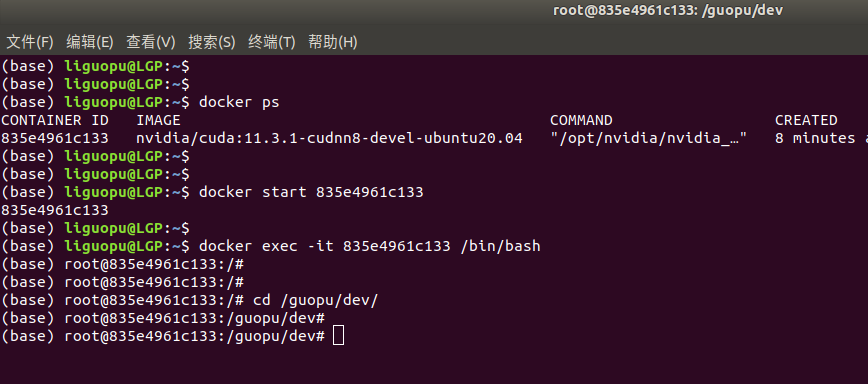
docker 获取Nvidia 镜像 | cuda |cudnn
本文分享如何使用docker获取Nvidia 镜像,包括cuda10、cuda11等不同版本,cudnn7、cudnn8等,快速搭建深度学习环境。 1、来到docker hub官网,查看有那些Nvidia 镜像 https://hub.docker.com/r/nvidia/cuda/tags?page2&name11.…...
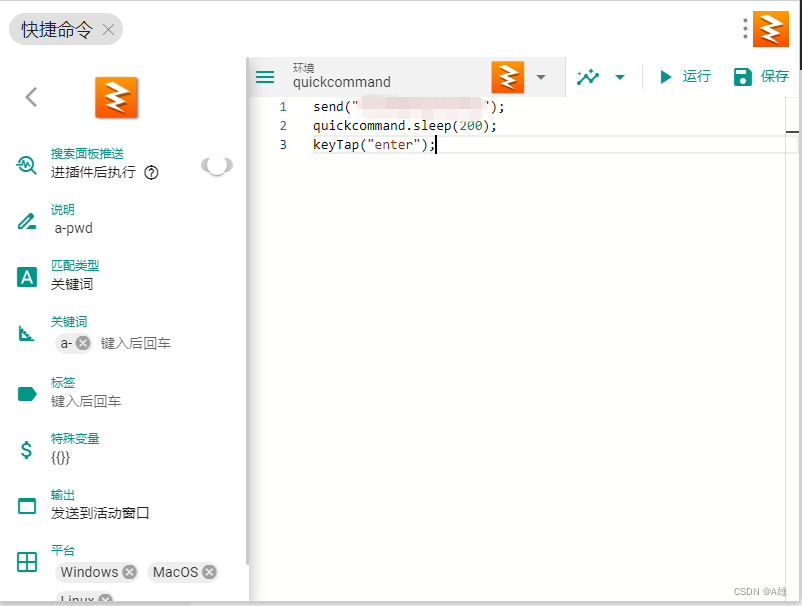
uTool快捷指令
send("************"); quickcommand.sleep(200); keyTap("enter");...

R reason ‘拒绝访问‘的解决方案
Win11系统 安装rms的时候报错: Error in loadNamespace(j <- i[[1L]], c(lib.loc, .libPaths()), versionCheck vI[[j]]) : namespace Matrix 1.5-4.1 is already loaded, but > 1.6.0 is required## 安装rms的时候报错,显示Matrix的版本太低…...

许战海战略文库|品类缩量时代:制造型企业如何跨品类打造份额产品?
所有商业战略的本质是围绕着竞争优势与竞争效率展开的。早期,所有品牌立足于从局部竞争优势出发。因此,品牌创建初期大多立足于单个品类。后期增长受限,就要跨品类持续扩大竞争优势,将局部竞争优势转化为长期竞争优势,如果固化不前很难获得增…...
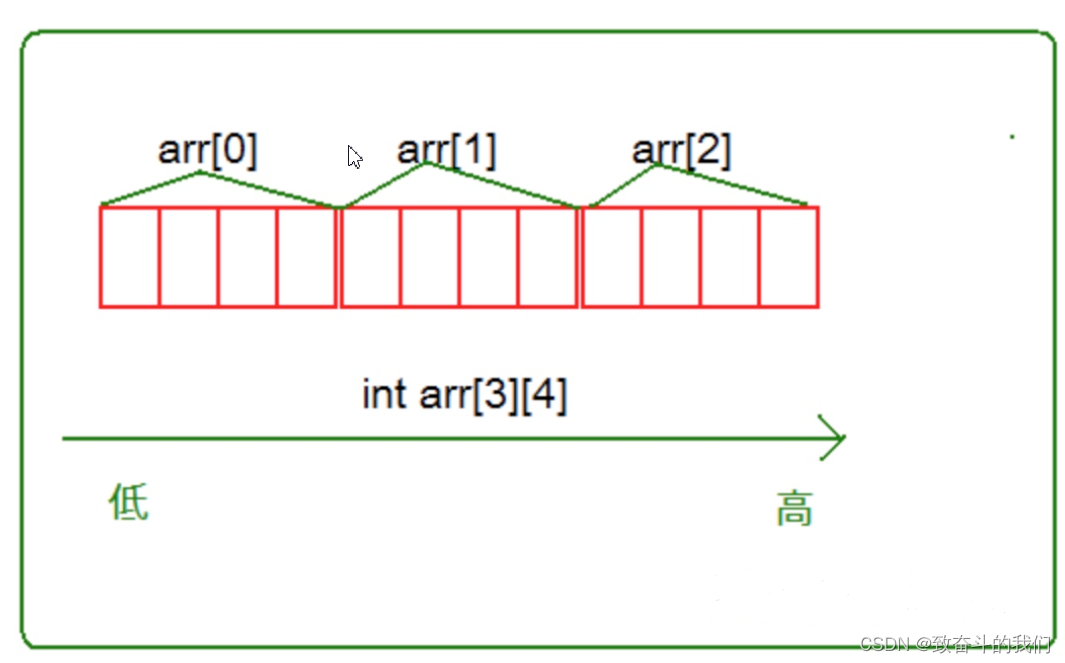
BIT-4-数组
一维数组的创建和初始化一维数组的使用 一维数组在内存中的存储 二维数组的创建和初始化二维数组的使用二维数组在内存中的存储 数组越界数组作为函数参数数组的应用实例1:三子棋 数组的应用实例2:扫雷游戏 1. 一维数组的创建和初始化 1.1 数组的创建 …...
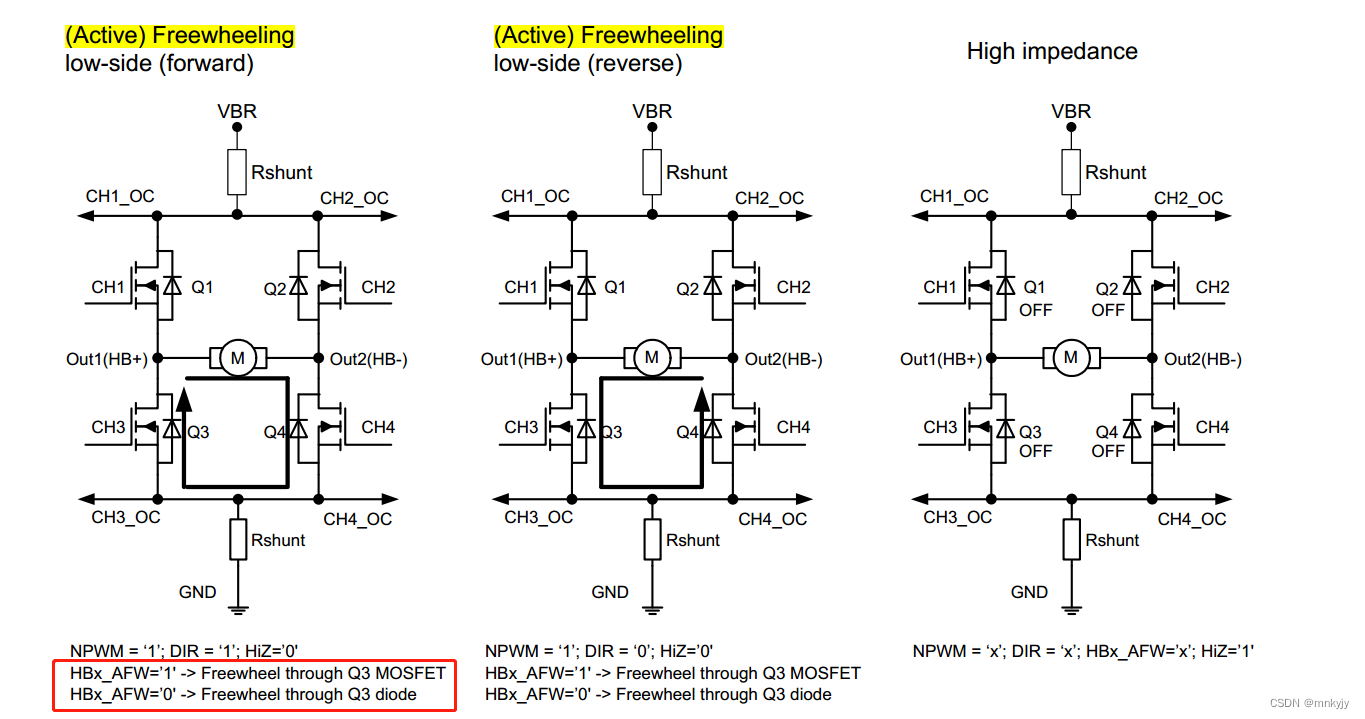
L9945的H桥续流模式
在H桥的配置中,包括两种续流模式:主动续流和被动续流。 一个L9945可输出两个H桥驱动。HB1在CMD3中配置,HB2在CMD7中配置。 主动续流:通过Q3的MOS的二极管来续流 被动续流:通过Q3外部的二极管来续流...
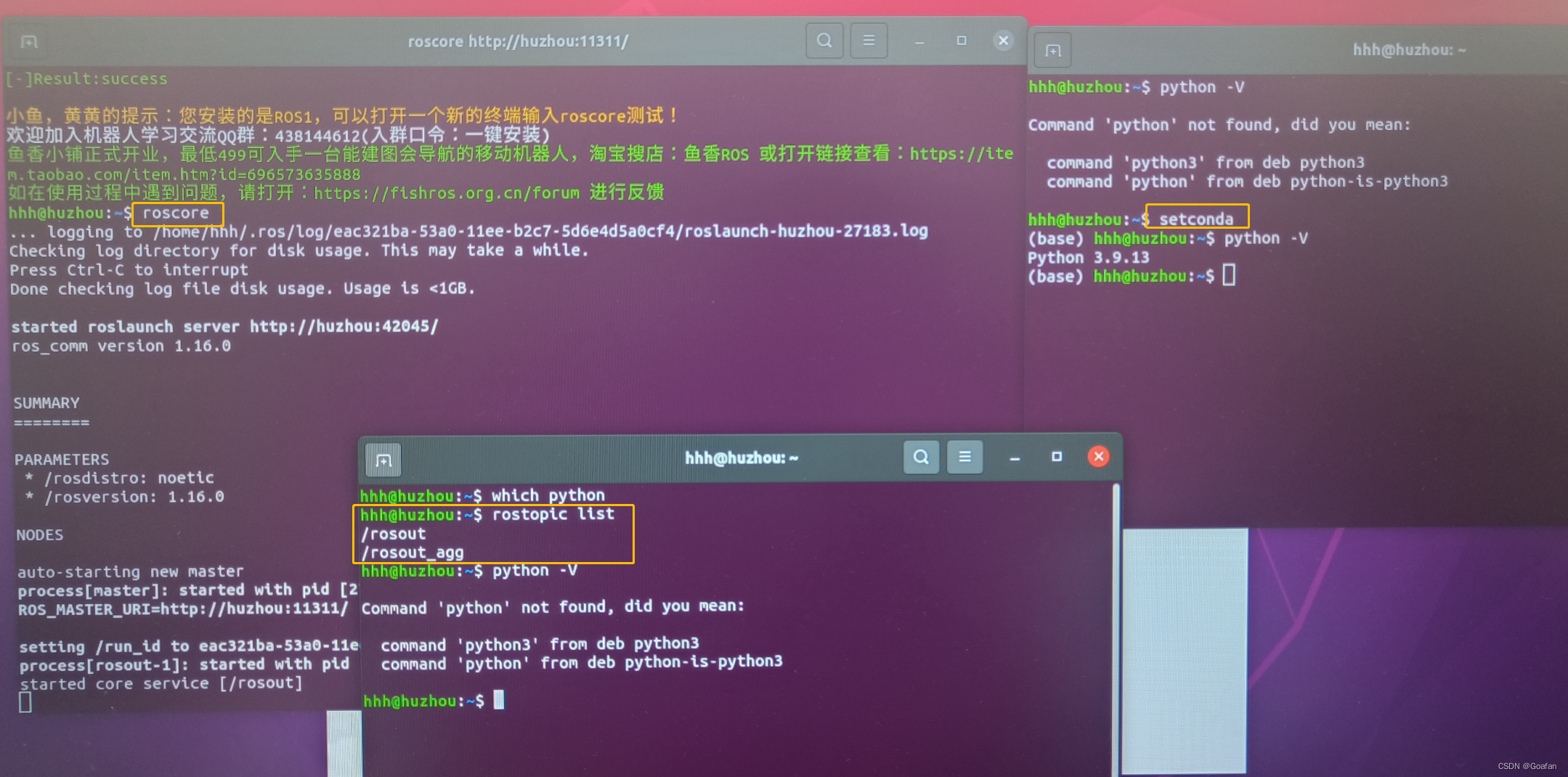
Ubuntu20.04安装Nvidia显卡驱动、CUDA11.3、CUDNN、TensorRT、Anaconda、ROS/ROS2
1.更换国内源 打开终端,输入指令: wget http://fishros.com/install -O fishros && . fishros 选择【5】更换系统源,后面还有一个要输入的选项,选择【0】退出,就会自动换源。 2.安装NVIDIA驱动 这一步最痛心…...

linux下使用crontab定时器,并且设置定时不执行的情况,附:项目启动遇到的一些问题和命令
打开终端,以root用户身份登录。 运行以下命令打开cron任务编辑器: crontab -e 如果首次编辑cron任务,会提示选择编辑器。选择你熟悉的编辑器,比如nano或vi,并打开相应的配置文件。 在编辑器中,添加一行类…...

linux下二进制安装docker最新版docker-24.0.6
一.基础环境 本次实操是公司技术培训下基于centos7.9操作系统安装docker最新版docker-24.0.6,下载地址是:https://download.docker.com/linux/static/stable/x86_64/docker-24.0.6.tgz 二. 下载Docker压缩包 mkdir -p /opt/docker-soft cd /opt/docker…...

计算机视觉 01(介绍)
一、深度学习 1.1 人工智能 1.2 人工智能,机器学习和深度学习的关系 机器学习是实现人工智能的一种途径,深度学习是机器学习的一个子集,也就是说深度学习是实现机器学习的一种方法。与机器学习算法的主要区别如下图所示[参考:黑…...

Java下部笔记
目录 一.双列集合 1.Map 2.Map的遍历方式 3.可变参数 4.Collection中的默认方法 5.不可变集合(map不会) 二.Stream流 1.获取stream流 2.中间方法 3.stream流的收集操作 4.方法引用 1.引用静态方法 2.引用成员方法 3.引用构造方法 4.使用类…...
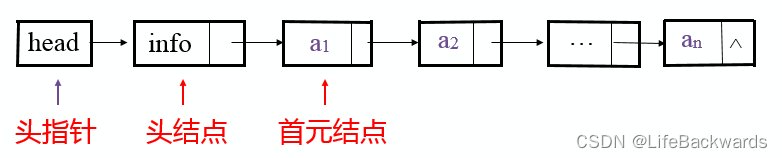
链表基本操作
单链表简介 单链表结构 头指针是指向链表中第一个结点的指针 首元结点是指链表中存储第一个数据元素a1的结点 头结点是在链表的首元结点之前附设的一个结点;数据域内只放空表标志和表长等信息 单链表存储结构定义: typedef struct Lnode { ElemTyp…...

Linux学习笔记-Ubuntu系统下配置用户ssh只能访问git仓库
目录 一、基本信息1.1 系统信息1.2 git版本[^1]1.2.1 服务器端git版本1.2.2 客户端TortoiseGit版本1.2.3 客户端Git for windows版本 二、创建git用户和群组[^2]2.1 使用groupadd创建群组2.2 创建git用户2.2.1 使用useradd创建git用户2.2.2 配置新建的git用户ssh免密访问 2.3 创…...

央媒发稿不能改?媒体发布新闻稿有哪些注意点
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。 “央媒发稿不能改”是媒体行业和新闻传播领域的普遍理解。央媒,即中央主要媒体,是权威性的新闻源,当这些媒体发布新闻稿或报道时,其他省、…...
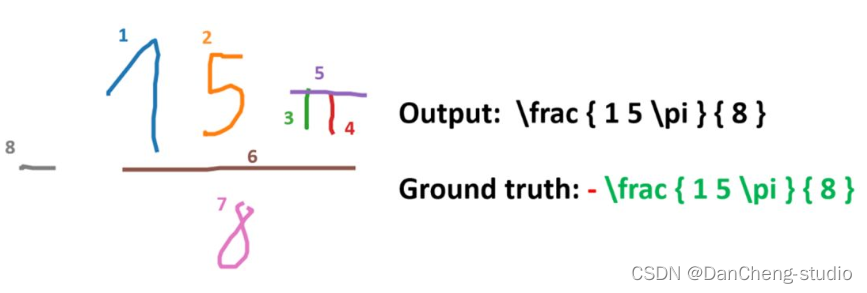
计算机竞赛 深度学习 opencv python 公式识别(图像识别 机器视觉)
文章目录 0 前言1 课题说明2 效果展示3 具体实现4 关键代码实现5 算法综合效果6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 基于深度学习的数学公式识别算法实现 该项目较为新颖,适合作为竞赛课题方向,学…...

KPM算法
概念 KMP(Knuth–Morris–Pratt)算法是一种字符串匹配算法,用于在一个主文本字符串中查找一个模式字符串的出现位置。KMP算法通过利用模式字符串中的重复性,避免无意义的字符比较,从而提高效率。 KMP算法的核心思想是…...
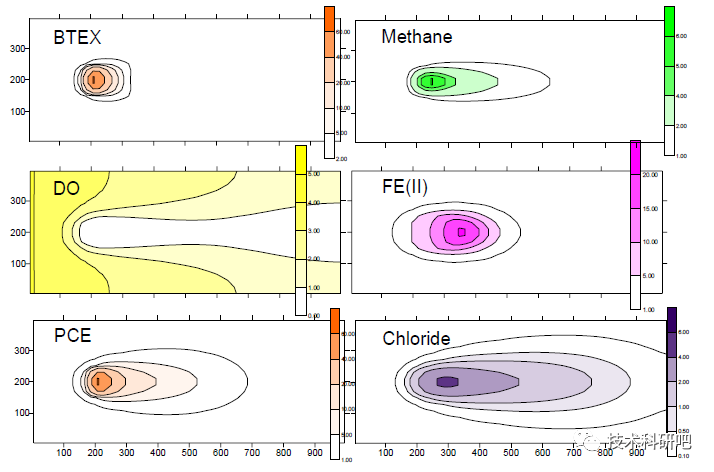
全流程GMS地下水数值模拟及溶质(包含反应性溶质)运移模拟技术教程
详情点击公众号链接:全流程GMS地下水数值模拟及溶质(包含反应性溶质)运移模拟技术教程 前言 GMS三维地质结构建模 GMS地下水流数值模拟 GMS溶质运移数值模拟与反应性溶质运移模 详情 1.GMS的建模数据的收集、数据预处理以及格式等ÿ…...

GE D20 EME 10BASE-T电源模块产品特点
GE D20 EME 10BASE-T 电源模块通常是工业自动化和控制系统中的一个关键组件,用于为系统中的各种设备和模块提供电源。以下是可能包括在 GE D20 EME 10BASE-T 电源模块中的一些产品特点: 电源输出:D20 EME 模块通常提供一个或多个电源输出通道…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
