怒刷LeetCode的第2天(Java版)
目录
第一题
题目来源
题目内容
解决方法
方法一:滑动窗口
方法二:双指针加哈希表
第二题
题目来源
题目内容
解决方法
方法一:二分查找
方法二:归并排序
方法三:分治法
第三题
题目来源
题目内容
解决方法
方法一:动态规划
方法二:中心扩展法
方法三:Manacher 算法
第一题
题目来源
3. 无重复字符的最长子串 - 力扣(LeetCode)
题目内容

解决方法
方法一:滑动窗口
该问题可以使用滑动窗口算法来解决。滑动窗口是一种通过移动窗口的起始和结束位置来解决字符串/数组子串问题的常用技巧。
具体算法步骤如下:
- 定义一个哈希集合,用于存储当前窗口中的字符。
- 使用两个指针left和right分别表示窗口的起始和结束位置,初始化为0。
- 使用一个循环遍历字符串s,不断移动右指针来扩展窗口。当右指针指向的字符在哈希集合中存在时,说明窗口中出现了重复字符。
- 在每一次循环中,首先判断右指针指向的字符是否在哈希集合中存在,如果不存在,则将该字符加入集合,并更新最长无重复子串的长度为maxLen(即maxLen = max(maxLen, right - left + 1))。
- 如果右指针指向的字符在哈希集合中存在,则从窗口的左侧开始移动左指针,直到窗口中不再有重复字符。
- 重复步骤3-5,直到右指针到达字符串s的末尾。
- 返回最长无重复子串的长度maxLen。
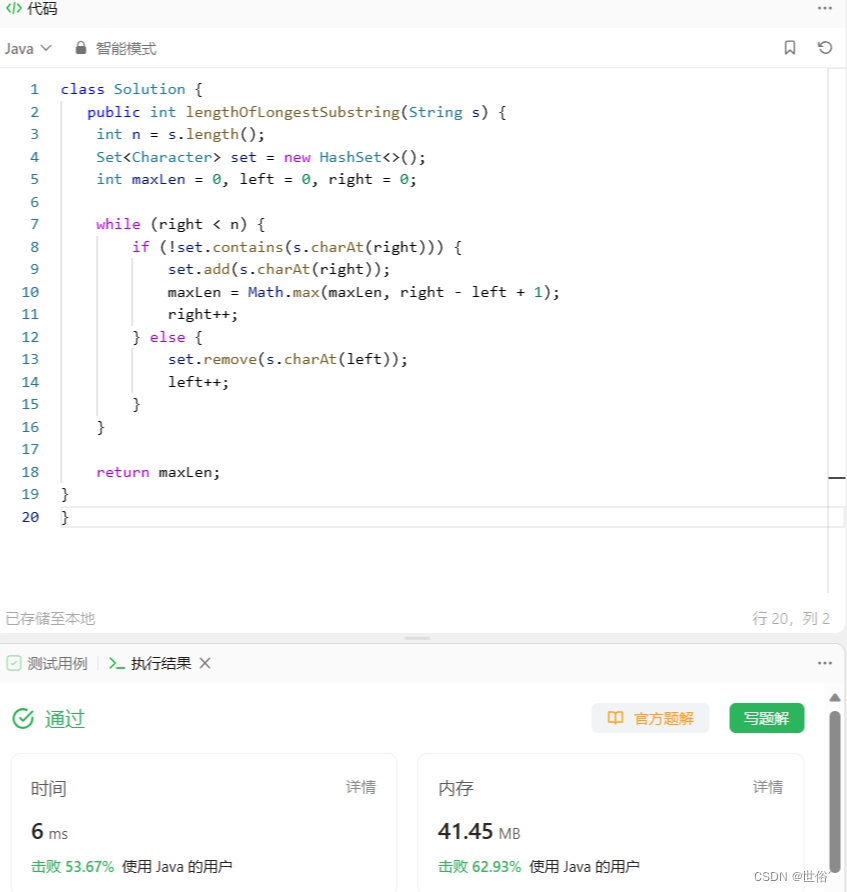
class Solution {public int lengthOfLongestSubstring(String s) {int n = s.length();Set<Character> set = new HashSet<>();int maxLen = 0, left = 0, right = 0;while (right < n) {if (!set.contains(s.charAt(right))) {set.add(s.charAt(right));maxLen = Math.max(maxLen, right - left + 1);right++;} else {set.remove(s.charAt(left));left++;}}return maxLen;
}
}该算法的时间复杂度为O(n),其中n是字符串s的长度。在最坏情况下,每个字符都需要遍历一次。空间复杂度为O(min(n, m)),其中m是字符集的大小。在最坏情况下,窗口中可能包含所有的字符。
LeetCode运行结果:
方法二:双指针加哈希表
除了滑动窗口算法之外,还可以使用双指针加哈希表来解决该问题。
具体算法步骤如下:
- 定义一个哈希表map,用于存储字符和它在字符串中出现的位置。
- 使用两个指针left和right分别表示当前无重复子串的起始和结束位置,初始化为0。
- 使用一个循环遍历字符串s,不断移动右指针来扩展窗口。当右指针指向的字符在哈希表中存在时,说明窗口中出现了重复字符。
- 在每一次循环中,首先判断右指针指向的字符是否在哈希表中存在,如果不存在,则将该字符加入哈希表,并更新最长无重复子串的长度为maxLen(即maxLen = max(maxLen, right - left + 1))。
- 如果右指针指向的字符在哈希表中存在,则从哈希表中获取该字符最新的出现位置pos,并将左指针移动到pos+1的位置。
- 更新哈希表中该字符的最新出现位置为右指针指向的位置right+1(注意要加1,因为要排除当前字符的影响),然后将右指针继续右移一位。
- 重复步骤3-6,直到右指针到达字符串s的末尾。
- 返回最长无重复子串的长度maxLen。
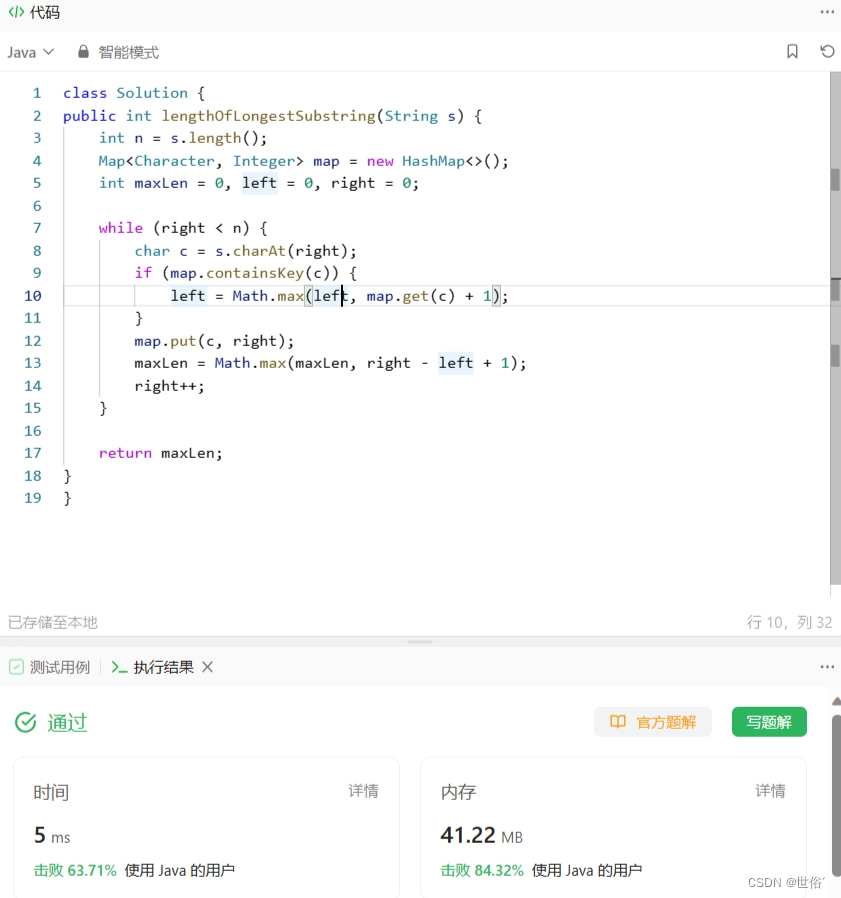
class Solution {
public int lengthOfLongestSubstring(String s) {int n = s.length();Map<Character, Integer> map = new HashMap<>();int maxLen = 0, left = 0, right = 0;while (right < n) {char c = s.charAt(right);if (map.containsKey(c)) {left = Math.max(left, map.get(c) + 1);}map.put(c, right);maxLen = Math.max(maxLen, right - left + 1);right++;}return maxLen;
}
}该算法的时间复杂度为O(n),其中n是字符串s的长度。在最坏情况下,每个字符都需要遍历一次。空间复杂度为O(min(n, m)),其中m是字符集的大小。在最坏情况下,哈希表中可能包含所有的字符。
LeetCode运行结果:
第二题
题目来源
4. 寻找两个正序数组的中位数 - 力扣(LeetCode)
题目内容

解决方法
方法一:二分查找
本题可以使用二分查找求解,时间复杂度为O(log(min(m, n)))。
由于两个数组都是有序的,所以可以先将问题转化为寻找第k小的数,其中k等于两个数组的长度之和除以2。如果两个数组长度之和是奇数,则中位数就是第k小的数;如果长度之和是偶数,则中位数是第k小和第k+1小数的平均值。
具体算法如下:
- 设两个有序数组为nums1和nums2,分别对它们进行二分查找。
- 假设nums1的长度为m,nums2的长度为n,则第k小的数就是最小的第k/2个数。
- 比较nums1[k/2-1]和nums2[k/2-1]。如果nums1[k/2-1] < nums2[k/2-1],说明nums1中的前k/2个数一定包含在中位数的前k个数中。反之,如果nums1[k/2-1] > nums2[k/2-1],说明nums2中的前k/2个数一定包含在中位数的前k个数中。
- 根据步骤3中的比较结果,确定接下来需要在哪个子数组中查找,然后递归调用本函数,更新k和目标数组。特别注意,每次递归调用时,都需要更新数组的起始下标,使得两个子数组的长度之和为k。
- 重复步骤3-4,直到k为1或者有一个数组为空,则中位数即为两个数组中剩余元素的第一个。
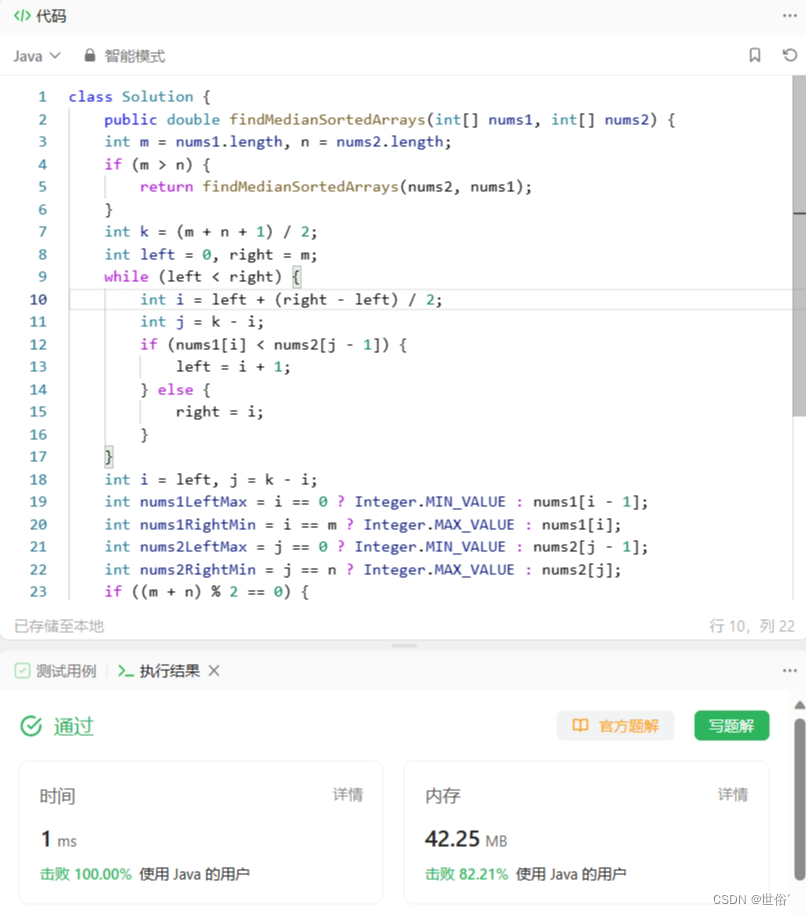
class Solution {public double findMedianSortedArrays(int[] nums1, int[] nums2) {int m = nums1.length, n = nums2.length;if (m > n) {return findMedianSortedArrays(nums2, nums1);}int k = (m + n + 1) / 2;int left = 0, right = m;while (left < right) {int i = left + (right - left) / 2;int j = k - i;if (nums1[i] < nums2[j - 1]) {left = i + 1;} else {right = i;}}int i = left, j = k - i;int nums1LeftMax = i == 0 ? Integer.MIN_VALUE : nums1[i - 1];int nums1RightMin = i == m ? Integer.MAX_VALUE : nums1[i];int nums2LeftMax = j == 0 ? Integer.MIN_VALUE : nums2[j - 1];int nums2RightMin = j == n ? Integer.MAX_VALUE : nums2[j];if ((m + n) % 2 == 0) {return (Math.max(nums1LeftMax, nums2LeftMax) + Math.min(nums1RightMin, nums2RightMin)) / 2.0;} else {return Math.max(nums1LeftMax, nums2LeftMax);}
}}该算法的时间复杂度为O(log(min(m, n))),空间复杂度为O(1)。
LeetCode运行结果:
方法二:归并排序
还有另一种方法可以解决这个问题,即使用归并排序的思想。具体步骤如下:
- 创建一个新的数组,用于存储合并后的两个有序数组。
- 使用两个指针分别指向nums1和nums2的起始位置。
- 每次比较两个数组当前指针所指的元素,将较小的元素添加到新数组中,并将对应的指针向后移动一位。
- 重复步骤3,直到其中一个数组的指针到达末尾。
- 将另一个数组剩余的元素依次添加到新数组的末尾。
- 如果新数组的长度是奇数,则中位数就是新数组的中间元素;如果新数组的长度是偶数,则中位数是中间两个元素的平均值。
该方法的时间复杂度为O(m + n),其中m和n分别是两个数组的长度。空间复杂度为O(m + n),主要用于存储合并后的数组。
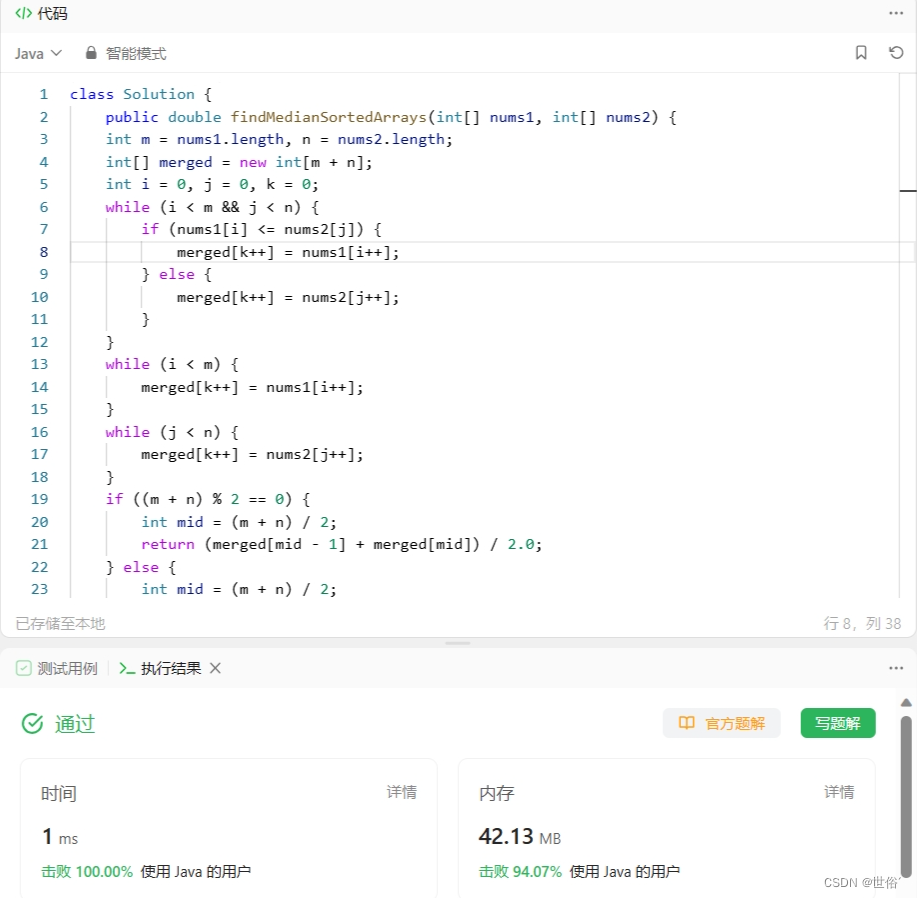
class Solution {public double findMedianSortedArrays(int[] nums1, int[] nums2) {int m = nums1.length, n = nums2.length;int[] merged = new int[m + n];int i = 0, j = 0, k = 0;while (i < m && j < n) {if (nums1[i] <= nums2[j]) {merged[k++] = nums1[i++];} else {merged[k++] = nums2[j++];}}while (i < m) {merged[k++] = nums1[i++];}while (j < n) {merged[k++] = nums2[j++];}if ((m + n) % 2 == 0) {int mid = (m + n) / 2;return (merged[mid - 1] + merged[mid]) / 2.0;} else {int mid = (m + n) / 2;return merged[mid];}
}}LeetCode运行结果:
方法三:分治法
除了上述两种方法,还可以使用分治法来解决这个问题。该方法的思路是将问题分解为两个子问题,然后对子问题进行递归求解。
具体步骤如下:
- 分别找到两个数组的中位数,假设分别为nums1[mid1]和nums2[mid2],其中mid1和mid2分别表示两个数组的中间位置。
- 如果nums1[mid1]等于nums2[mid2],则说明中位数已经找到,直接返回nums1[mid1]或nums2[mid2]。
- 如果nums1[mid1]小于nums2[mid2],则说明中位数应该在nums1[mid1]的右侧和nums2[mid2]的左侧。
- 在nums1[mid1]的右侧舍弃掉前mid1+1个元素,并且将k减去mid1+1。
- 在nums2[mid2]的左侧舍弃掉后mid2个元素。
- 如果nums1[mid1]大于nums2[mid2],则说明中位数应该在nums1[mid1]的左侧和nums2[mid2]的右侧。
- 在nums1[mid1]的左侧舍弃掉后mid1个元素。
- 在nums2[mid2]的右侧舍弃掉前mid2+1个元素,并且将k减去mid2+1。
- 重复上述步骤3和步骤4,直到找到中位数为止。
这种方法的时间复杂度也为O(log(min(m, n))),空间复杂度为O(1)。与二分查找类似,它通过逐渐缩小问题规模来快速找到中位数。
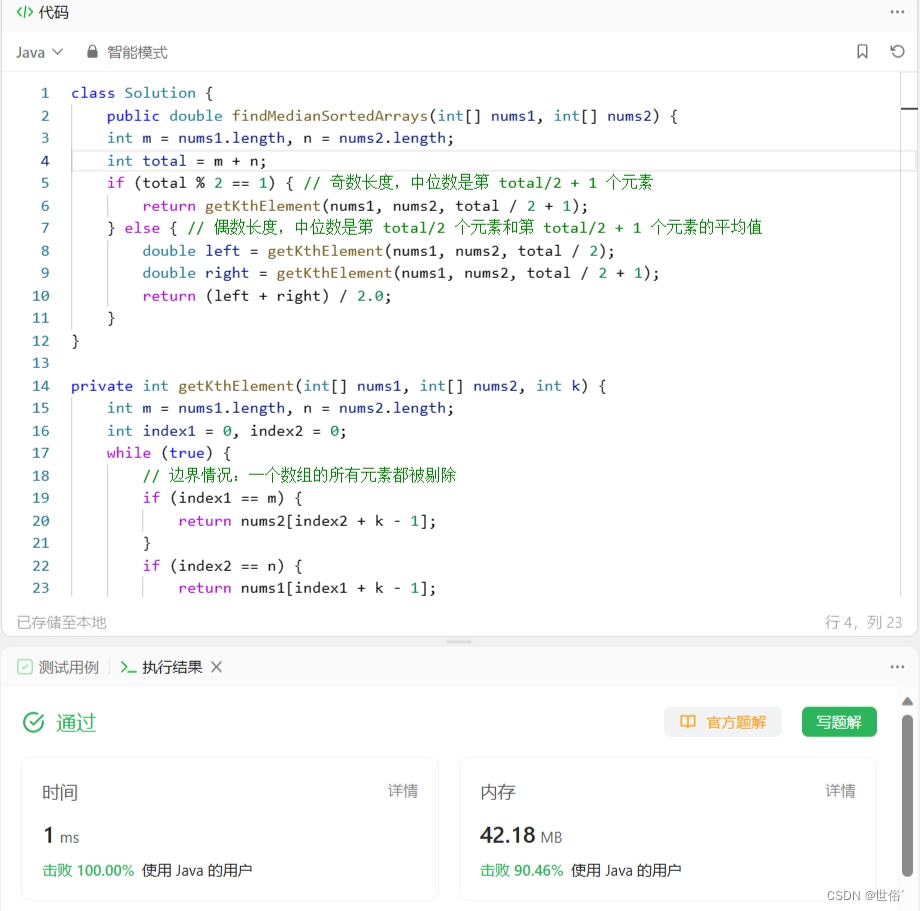
class Solution {public double findMedianSortedArrays(int[] nums1, int[] nums2) {int m = nums1.length, n = nums2.length;int total = m + n;if (total % 2 == 1) { // 奇数长度,中位数是第 total/2 + 1 个元素return getKthElement(nums1, nums2, total / 2 + 1);} else { // 偶数长度,中位数是第 total/2 个元素和第 total/2 + 1 个元素的平均值double left = getKthElement(nums1, nums2, total / 2);double right = getKthElement(nums1, nums2, total / 2 + 1);return (left + right) / 2.0;}
}private int getKthElement(int[] nums1, int[] nums2, int k) {int m = nums1.length, n = nums2.length;int index1 = 0, index2 = 0;while (true) {// 边界情况:一个数组的所有元素都被剔除if (index1 == m) {return nums2[index2 + k - 1];}if (index2 == n) {return nums1[index1 + k - 1];}// 边界情况:k=1,即找到了最小的一个数if (k == 1) {return Math.min(nums1[index1], nums2[index2]);}// 正常情况int newIndex1 = Math.min(index1 + k / 2, m) - 1;int newIndex2 = Math.min(index2 + k / 2, n) - 1;int pivot1 = nums1[newIndex1], pivot2 = nums2[newIndex2];if (pivot1 <= pivot2) {k -= newIndex1 - index1 + 1;index1 = newIndex1 + 1;} else {k -= newIndex2 - index2 + 1;index2 = newIndex2 + 1;}}
}}LeetCode运行结果:
第三题
题目来源
5. 最长回文子串 - 力扣(LeetCode)
题目内容

解决方法
方法一:动态规划
这道题可以使用动态规划来解决,具体步骤如下:
- 定义一个二维布尔数组dp,其中dp[i][j]表示字符串s中从索引i到索引j的子串是否是回文子串。初始化时,将所有的dp[i][i]设为true,表示单个字符都是回文串。
- 从右下角开始,按列从下往上逐列填表。先计算长度为2的子串是否是回文子串,再计算长度为3的子串,依次类推,直到计算出整个字符串的最长回文子串长度为止。
如果dp[i+1][j-1]为true(即子串s[i+1:j-1]也是回文子串)且s[i]等于s[j],则dp[i][j]为true,否则为false。 - 在计算的过程中,记录并更新最长回文子串的起始索引和长度。
- 最后,根据最长回文子串的起始索引和长度,提取出最长回文子串。
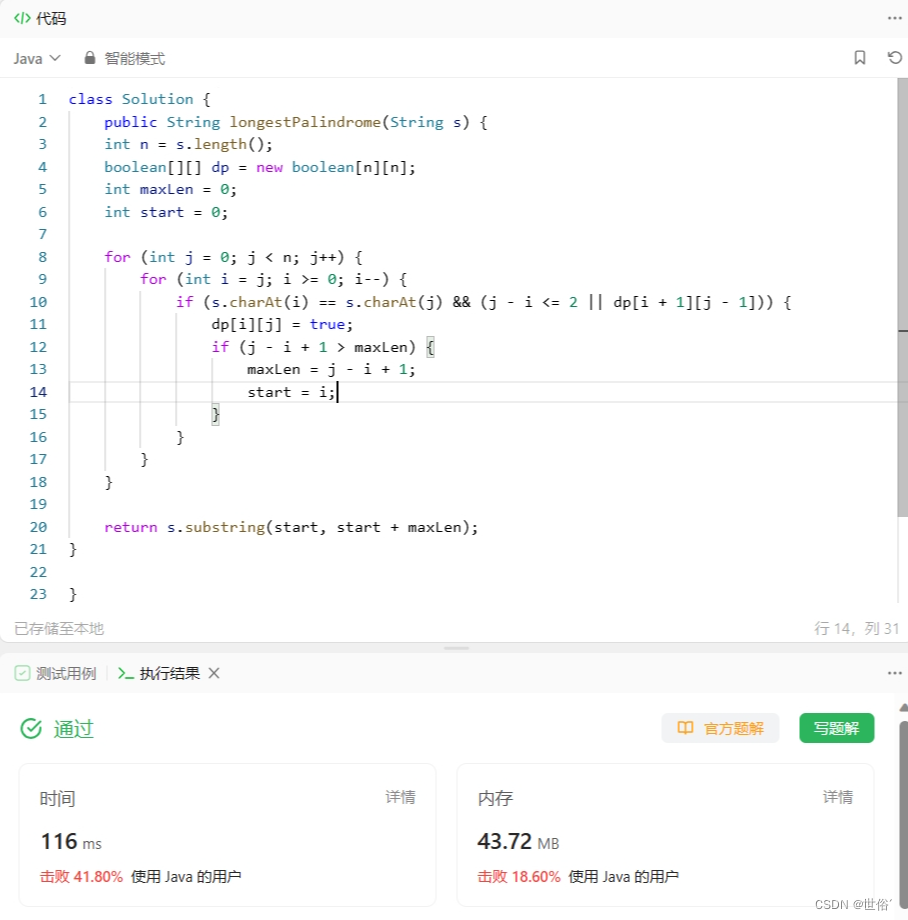
class Solution {public String longestPalindrome(String s) {int n = s.length();boolean[][] dp = new boolean[n][n];int maxLen = 0;int start = 0;for (int j = 0; j < n; j++) {for (int i = j; i >= 0; i--) {if (s.charAt(i) == s.charAt(j) && (j - i <= 2 || dp[i + 1][j - 1])) {dp[i][j] = true;if (j - i + 1 > maxLen) {maxLen = j - i + 1;start = i;}}}}return s.substring(start, start + maxLen);
}}该算法的时间复杂度为O(n^2),空间复杂度为O(n^2),其中n为字符串的长度。通过动态规划,我们可以高效地找到最长回文子串。
LeetCode运行结果:
方法二:中心扩展法
除了动态规划方法外,还可以使用中心扩展法来解决这个问题。
中心扩展法的思路是,对于每个字符或每对相邻字符,以它们为中心向两边扩展,判断是否是回文串。具体步骤如下:
- 遍历字符串中的每个字符,将每个字符作为中心(回文串长度为奇数的情况)或相邻字符的中间位置(回文串长度为偶数的情况)。
- 在每个中心位置,使用双指针,从中心向两边扩展,判断左右的字符是否相等,直到无法再扩展为止。
- 在扩展过程中,记录并更新最长回文子串的起始索引和长度。
- 最后,根据最长回文子串的起始索引和长度,提取出最长回文子串。
class Solution {public String longestPalindrome(String s) {int n = s.length();int start = 0, maxLen = 0;for (int i = 0; i < n; i++) {// 中心为一个字符的情况int len1 = expandAroundCenter(s, i, i);// 中心为相邻字符的情况int len2 = expandAroundCenter(s, i, i + 1);int len = Math.max(len1, len2);if (len > maxLen) {maxLen = len;// 根据中心和回文串长度计算起始索引start = i - (len - 1) / 2;}}return s.substring(start, start + maxLen);
}private int expandAroundCenter(String s, int left, int right) {while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {left--;right++;}// 扩展的长度为 right-left-1,减1是因为不满足条件时left和right多移动了一步return right - left - 1;
}
}该算法的时间复杂度为O(n^2),空间复杂度为O(1),其中n为字符串的长度。中心扩展法利用了回文串的特点,可以高效地找到最长回文子串。
LeetCode运行结果: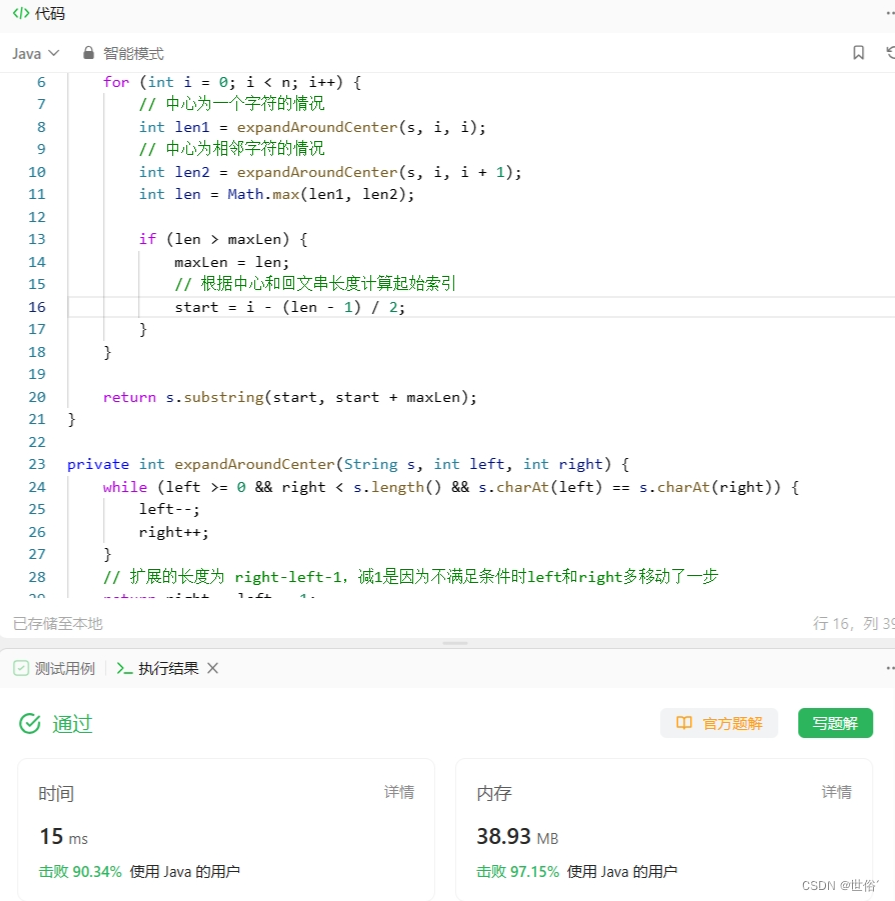
方法三:Manacher 算法
除了动态规划和中心扩展法之外,还有一种称为Manacher算法的线性时间算法可以用于查找最长回文子串。Manacher算法的核心思想是利用回文串的对称性,在遍历过程中尽量复用已经计算过的回文子串信息。
具体步骤如下:
- 首先,我们需要对原始字符串进行预处理,将其转换为一个新的字符串,这样可以将奇数长度和偶数长度的回文串统一处理。
- 在每个字符前后添加特殊字符(例如
#),以确保新字符串中的回文串长度都是奇数。 - 在新字符串的开头和结尾添加特殊字符(例如
$和%),以便处理边界情况。 - 新字符串的长度将是原始字符串长度的两倍加一。
- 在每个字符前后添加特殊字符(例如
- 定义一个辅助数组
P,其中P[i]表示以新字符串中索引i为中心的回文串的半径长度(包括中心字符在内)。- 使用两个变量
center和right来维护当前已经找到的最右边界的回文串的中心和右边界。 - 在遍历的过程中,逐个计算
P[i]的值。- 当
i在当前最右边界right的左侧时,使用对称性快速计算出初始猜测值,即P[i] = P[2 * center - i]。但如果该猜测值超出了最右边界,则需要修正为最右边界到边界之间的距离,即P[i] = right - i。 - 然后,利用中心扩展法向两边扩展,直到无法再扩展为止,更新
P[i]的值并更新最右边界。
- 当
- 使用两个变量
- 在遍历过程中,记录并更新最长回文子串的起始索引和长度。最长回文子串的长度即为
maxLen = max(P) - 1,起始索引为start = (maxP - 1) / 2。 - 最后,根据最长回文子串的起始索引和长度,提取出最长回文子串。
class Solution {public String longestPalindrome(String s) {int n = s.length();StringBuilder sb = new StringBuilder("$#");// 预处理字符串for (int i = 0; i < n; i++) {sb.append(s.charAt(i));sb.append("#");}sb.append("%");String str = sb.toString();int len = str.length();int[] P = new int[len];int center = 0, right = 0;int maxP = 0, maxLen = 0;for (int i = 1; i < len - 1; i++) {if (i < right) {int mirror = 2 * center - i;P[i] = Math.min(right - i, P[mirror]);}// 中心扩展while (str.charAt(i + P[i] + 1) == str.charAt(i - P[i] - 1)) {P[i]++;}// 更新最右边界if (i + P[i] > right) {center = i;right = i + P[i];}// 记录最长回文子串的起始索引和长度if (P[i] > maxLen) {maxLen = P[i];maxP = i;}}int start = (maxP - maxLen) / 2;return s.substring(start, start + maxLen);
}
}Manacher算法的时间复杂度为O(n),空间复杂度为O(n),其中n为字符串的长度。相比于动态规划和中心扩展法,Manacher算法在效率上具有优势,特别适用于处理大规模字符串。
LeetCode运行结果: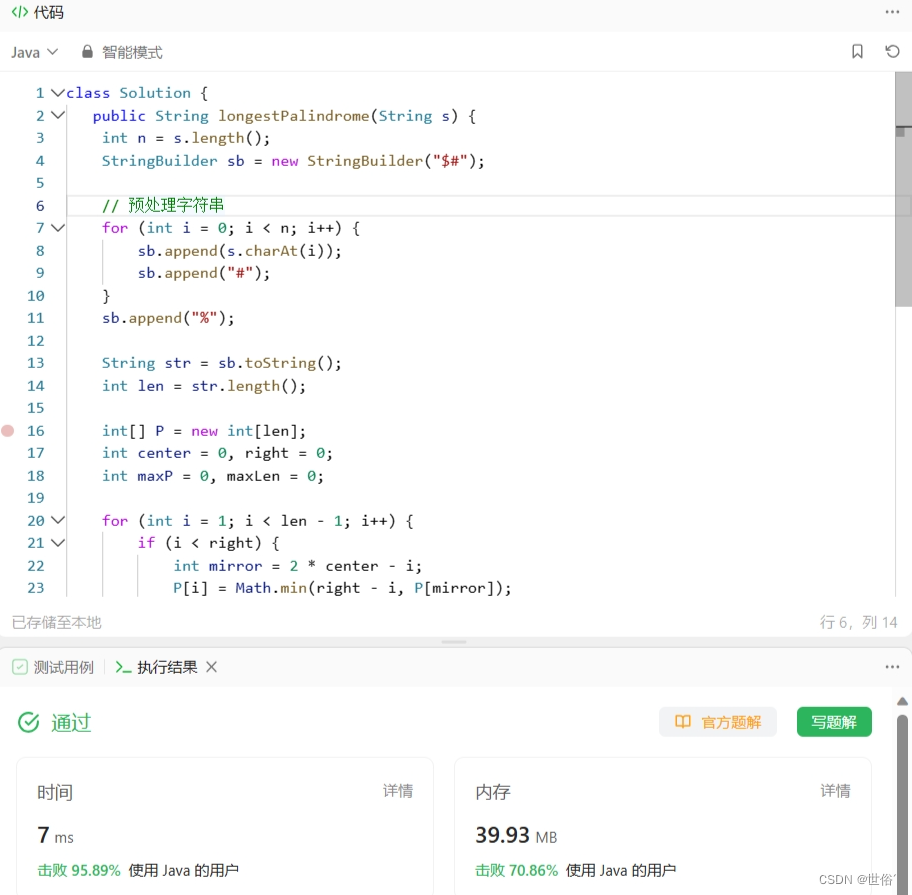
相关文章:

怒刷LeetCode的第2天(Java版)
目录 第一题 题目来源 题目内容 解决方法 方法一:滑动窗口 方法二:双指针加哈希表 第二题 题目来源 题目内容 解决方法 方法一:二分查找 方法二:归并排序 方法三:分治法 第三题 题目来源 题目内容 解…...
)
AUTOSAR汽车电子嵌入式编程精讲300篇-车载CAN总线网络的异常检测(续)
目录 车载 CAN 总线网络异常检测技术 3.1 车载 CAN 总线网络异常检测技术概述 3.1.1基于统计的异...
mojo安装
docker安装mojo 官网 https://developer.modular.com/login 很奇怪登录页面不显示 类似于网站劫持 docker 安装mojo带jupyterlab的方式 https://hub.docker.com/r/lmq886/mojojupyterlab 拉取镜像 docker pull lmq886/mojojupyterlab docker pull lmq886/mojojupyterlab:1.2 启…...

【探索Linux】—— 强大的命令行工具 P.8(进程地址空间)
阅读导航 前言一、内存空间分布二、什么是进程地址空间1. 概念2. 进程地址空间的组成 三、进程地址空间的设计原理1. 基本原理2. 虚拟地址空间 概念 大小和范围 作用 虚拟地址空间的优点 3. 页表 四、为什么要有地址空间五、总结温馨提示 前言 前面我们讲了C语言的基础知识&am…...
vue3 - Element Plus 切换主题色及el-button hover颜色不生效的解决方法
GitHub Demo 地址 在线预览 Element Plus 自定义主题官方文档 如果您想要通过 js 控制 css 变量,可以这样做: // document.documentElement 是全局变量时 const el document.documentElement // const el document.getElementById(xxx)// 获取 css 变…...

【C++面向对象侯捷】1.C++编程简介
文章目录 视频来源:我的百度网盘...
年龄大了转嵌入式有机会吗?
年龄大了转嵌入式有机会吗? 首先,说下结论:年龄并不是限制转行嵌入式软件开发的因素,只要具备一定的编程和电子基础知识,认真学习和实践,是可以成为优秀的嵌入式软件开发工程师的。最近很多小伙伴找我&…...
)
Mysql高级——索引优化和查询优化(2)
5. 排序优化 5.1 排序优化 问题:在 WHERE 条件字段上加索引,但是为什么在 ORDER BY 字段上还要加索引呢? 优化建议: SQL 中,可以在 WHERE 子句和 ORDER BY 子句中使用索引,目的是在 WHERE 子句中避免全表…...

SpringMVC的拦截器和JSR303的使用
目录 一、JSR303 二、拦截器(interceptor) 一、JSR303 1.1.什么是JSR303 JSR 303,它是Java EE(现在称为Jakarta EE)规范中的一部分。JSR 303定义了一种用于验证Java对象的标准规范,也称为Bean验证。 Bean验…...
servlet中doGet方法无法读取body中的数据
servlet中doGet方法不支持读取body中的数据。...

Ubuntu MongoDB账户密码设置
1.创建用户 在MongoDB中,可以使用db.createUser()方法来创建用户。该方法接受一个包含用户名、密码和角色等信息的文档作为参数。 // 连接到MongoDB数据库 mongo// 切换到admin数据库 use admin// 创建用户 db.createUser({user: "admin",pwd: "adm…...
)
指针进阶(3)
9. 模拟实现排序函数 这里我们使用冒泡排序算法,模拟实现一个排序函数,可以排序任意类型的数据。 这段代码可以排序整型数据,我们需要在这段代码的基础上进行改进,使得它可以排序任意类型的数据。 #define _CRT_SECURE_NO_WARN…...
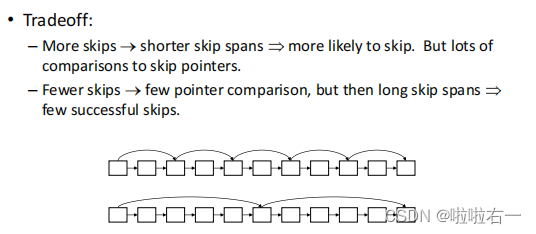
信息检索与数据挖掘 | (二)布尔检索与倒排索引
文章目录 📚词项-文档关联矩阵🐇相关名词🐇词项-文档关联矩阵的布尔查询处理 📚倒排索引🐇关于索引🐇建立索引🐇基于倒排索引的布尔查询处理🐇查询优化 📚字典数据结构&a…...

【学习笔记】EC-Final 2022 K. Magic
最近的题都只会抄题解😅 首先,操作顺序会影响答案,因此不能直接贪心。其次,因为是求贡献最大,所以可以考虑枚举最终哪些位置对答案产生了贡献,进而转化为全局贡献。 1.1 1.1 1.1 如果 [ l 1 , r 1 ) ⊆ [ …...
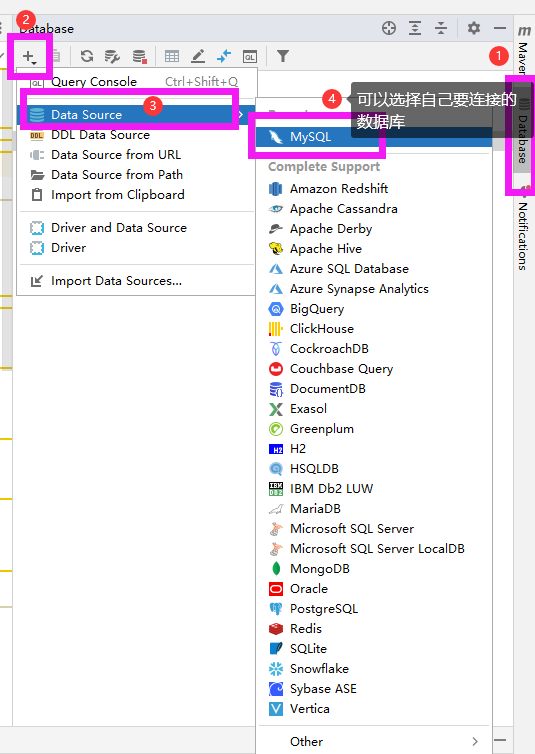
MySQL数据库笔记
文章目录 一、初识MySQL1.1、什么是数据库1.2、数据库分类1.3、MySQL简介 二、操作数据库2.1、操作数据库(了解)2.2、数据库的列类型2.3、数据库的字段属性(重点)2.4、创建数据库表(重点)2.5、数据表的类型…...
)
大数据之Hive(三)
分区表 概念和常用操作 将一个大表的数据按照业务需要分散存储到多个目录,每个目录称为该表的一个分区。一般来说是按照日期来作为分区的标准。在查询时可以通过where子句来选择查询所需要的分区,这样查询效率会提高很多。 ①创建分区表 hive (defau…...

让高分辨率的相机芯片输出低分辨率的图片对于像素级的值有什么影响?
很多图像传感器可以输出多个分辨率的图像,如果选择低分辨率格式的图像输出,对于图像本身会有什么影响呢? 传感器本身还是使用全部像素区域进行感光,但是在像素数据输出时会进行所谓的降采样(down-sampling)…...
FastGPT 接入飞书(不用写一行代码)
FastGPT V4 版本已经发布,可以通过 Flow 可视化进行工作流编排,从而实现复杂的问答场景,例如联网谷歌搜索,操作数据库等等,功能非常强大,还没用过的同学赶紧去试试吧。 飞书相比同类产品算是体验非常好的办…...
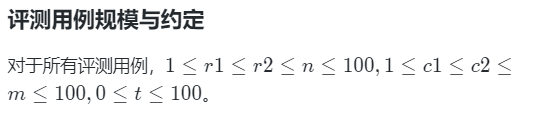
蓝桥杯 题库 简单 每日十题 day6
01 删除字符 题目描述 给定一个单词,请问在单词中删除t个字母后,能得到的字典序最小的单词是什么? 输入描述 输入的第一行包含一个单词,由大写英文字母组成。 第二行包含一个正整数t。 其中,单词长度不超过100&#x…...

使用Arduino简单测试HC-08蓝牙模块
目录 模块简介模块测试接线代码测试现象 总结 模块简介 HC-08 蓝牙串口通信模块是新一代的基于 Bluetooth Specification V4.0 BLE 蓝牙协议的数传模块。无线工作频段为 2.4GHz ISM,调制方式是 GFSK。模块最大发射功率为4dBm,接收灵度-93dBm,…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...
