Node.js 调用 fluent-ffmpeg
最近开发H5资源在线裁剪,最终在资源合成的步骤,选择 ffmpeg 作为合成的插件,记录下使用方式。
一、介绍
ffmpeg 一款跨平台多媒体处理工具,可以进行视频转码、裁剪、合成、音视频提取、推流等操作。
二、安装
Node js 可以利用 child_process 子进程调用 ffmpeg ,同时也可以利用 fluent-ffmpeg 插件来调用。
首先下载安装 ffmpeg, 选择 windows 环境,下载后解压到C盘,接着配置环境变量。
命令行执行 ffmpeg -version,走到这里说明安装成功
三、使用
我们这里就演示下基本功能,更多功能到 ffmpeg 官网尝试,下面是一段视频格式转换的逻辑,并伴随进度打印以及任务执行钩子函数
index.js
let express = require('express') // 引入express
let app = express() // 相当于 http.createServer(app)
let ffmpeg = require('fluent-ffmpeg') // ffmpeg
let { exceSync } = require('child_process')let command = ffmpeg('http://10.0.129.157:8000/2023_09_11_17_28_08_智慧教室A_默认授课_admin_/学生全景.mp4').on('start', function(commandLine) {console.log('Spawned Ffmpeg with command: ' + commandLine);}).on('progress', function(progress) {console.log('Processing: ' + progress.percent + '% done');}).on('end', function(stdout, stderr) {console.log('Transcoding succeeded !');}).on('error', function(err) {console.log('An error occurred: ' + err.message);}).save('test.avi')/*** @description create screenshots*/
function createScreenshots(command) {command.screenshots({folder: './',filename: 'test.png',count: 1,timemarks: [1],size: '50%'})
}
运行成功
预览转换格式后的视频:
相关文章:

Node.js 调用 fluent-ffmpeg
最近开发H5资源在线裁剪,最终在资源合成的步骤,选择 ffmpeg 作为合成的插件,记录下使用方式。 一、介绍 ffmpeg 一款跨平台多媒体处理工具,可以进行视频转码、裁剪、合成、音视频提取、推流等操作。 二、安装 Node js 可以利用…...

scrapy框架--
Scrapy是一个用于爬取数据的Python框架。下面是Scrapy框架的基本操作步骤: 安装Scrapy:首先,确保你已经安装好了Python和pip。然后,在命令行中运行以下命令安装Scrapy:pip install scrapy 创建Scrapy项目:…...

算法通关村第十五关——从40亿个数中产生一个不存在的数的处理方法
1.从40个亿中产生一个不存在的整数 题目要求:给定一个输入文件,包含40亿个非负整数,请设计一个算法,产生一个不存在该文件中的整数,假设你有1GB的内存来完成这项任务。**** 解题中心思想:存储的不是这40亿…...

软件项目开发的流程及关键点
软件项目开发的流程及关键点 graph LR A[需求分析] --> B[系统设计] B --> C[编码开发] C --> D[测试验证] D --> E[部署上线] E --> F[运维支持]在项目开发的流程中,首先是进行需求分析,明确项目的目标和功能要求。接下来是系统设计&am…...
)
全球变暖问题(floodfill 处理联通块问题)
全球变暖问题 文章目录 全球变暖问题前言题目描述题目分析边界问题的考虑岛屿是否被淹没判断:如何寻找联通块: 代码预告 前言 之前我们介绍了 bfs算法在二维,三维地图中的应用,现在我们接续进行拓展,解锁floodfill 算…...

由于找不到vcruntime140_1.dll怎么修复,详细修复步骤分享
在使用电脑过程中,可能会遇到一些错误提示,其中之一是找不到vcruntime140_1.dll的问题。这使得许多用户感到困扰,不知道该如何解决这个问题。小编将详细介绍vcruntime140_1.dll的作用以及解决找不到该文件的方法,帮助你摆脱困境。…...
)
算法 三数之和-(双指针)
牛客网: BM54 题目: 数组中所有不重复的满足三数之和等于0的数,非递减形式。 思路: 数组不小于3。不重复非递减,需先排序。使用idx从0开始遍历到n-2, 如果出现num[idx]num[idx-1]的情况,忽略继续下一个idx;令left idx1, right …...
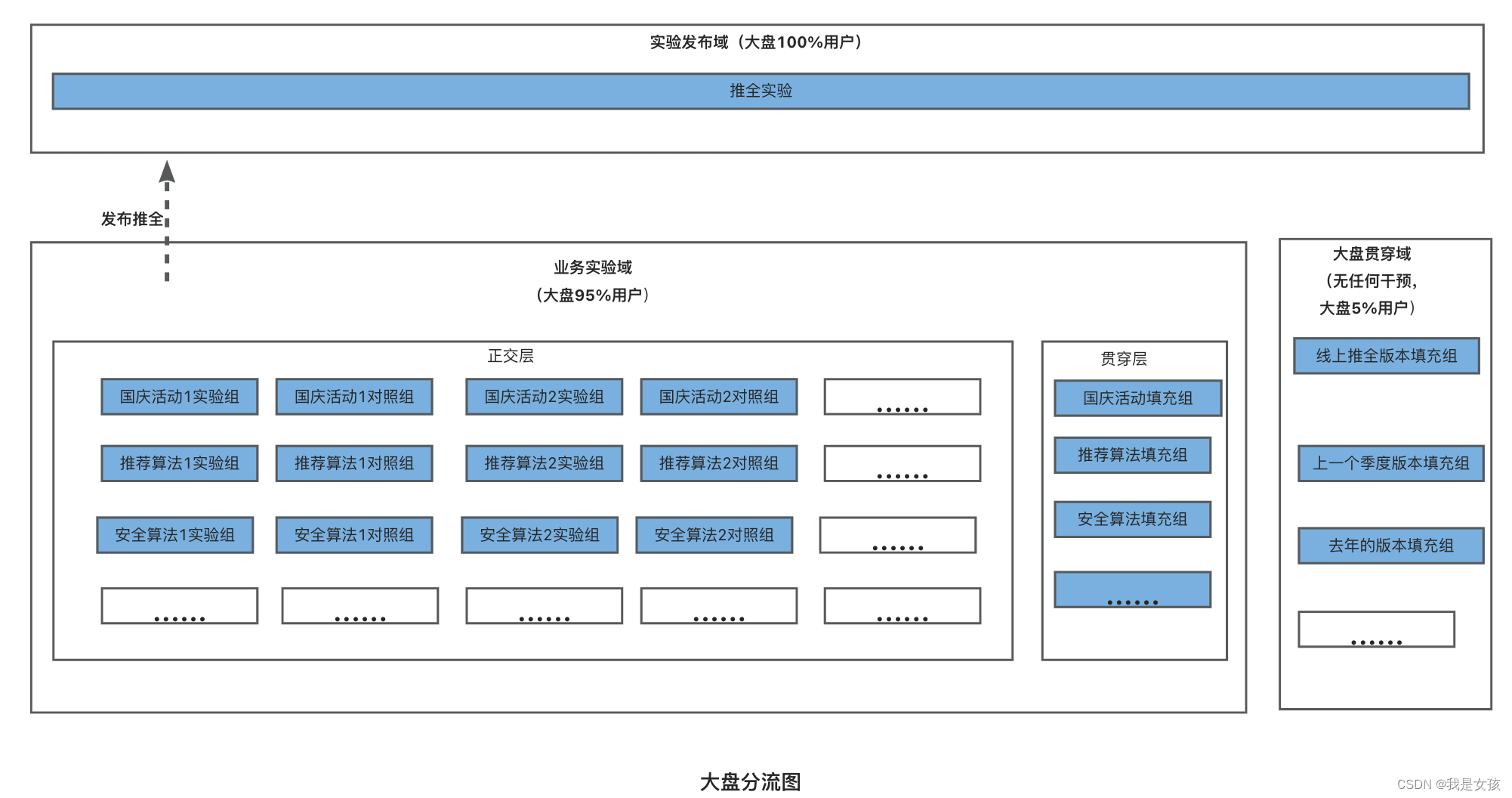
AB实验总结
互联网有线上系统,可做严格的AB实验。传统行业很多是不能做AB实验的。 匹配侧是采用严格的AB实验来进行模型迭代,而精细化定价是不能通过AB实验来评估模型好坏,经历过合成控制法、双重差分法,目前采用双重差分法来进行效果评估。…...

sklearn包中对于分类问题,如何计算accuracy和roc_auc_score?
1. 基础条件 import numpy as np from sklearn import metricsy_true np.array([1, 7, 4, 6, 3]) y_prediction np.array([3, 7, 4, 6, 3])2. accuracy_score计算 acc metrics.accuracy_score(y_true, y_prediction)这个没问题 3. roc_auc_score计算 The binary and mul…...

python温度转换程序
1.使用pycharm运行温度转换程序,尝试将温度单位设在前面 2.参照温度转换程序,自己写一个关于货币转换、长度转换、重量转换或者面积转换的程序 循环函数 def convertemperature():temperature ""while (temperature ! "q"):temperature in…...

Vue2中10种组件通信方式和实践技巧
目录 1,props / $emit1.1,一个需求方法1方法2 1.2,v-model 和 .syncv-model.sync 2,$children / $parent3,ref4,$attrs / $listeners$attrs$listenersinheritAttrs1.1 的问题的第3种解决方法 5,…...
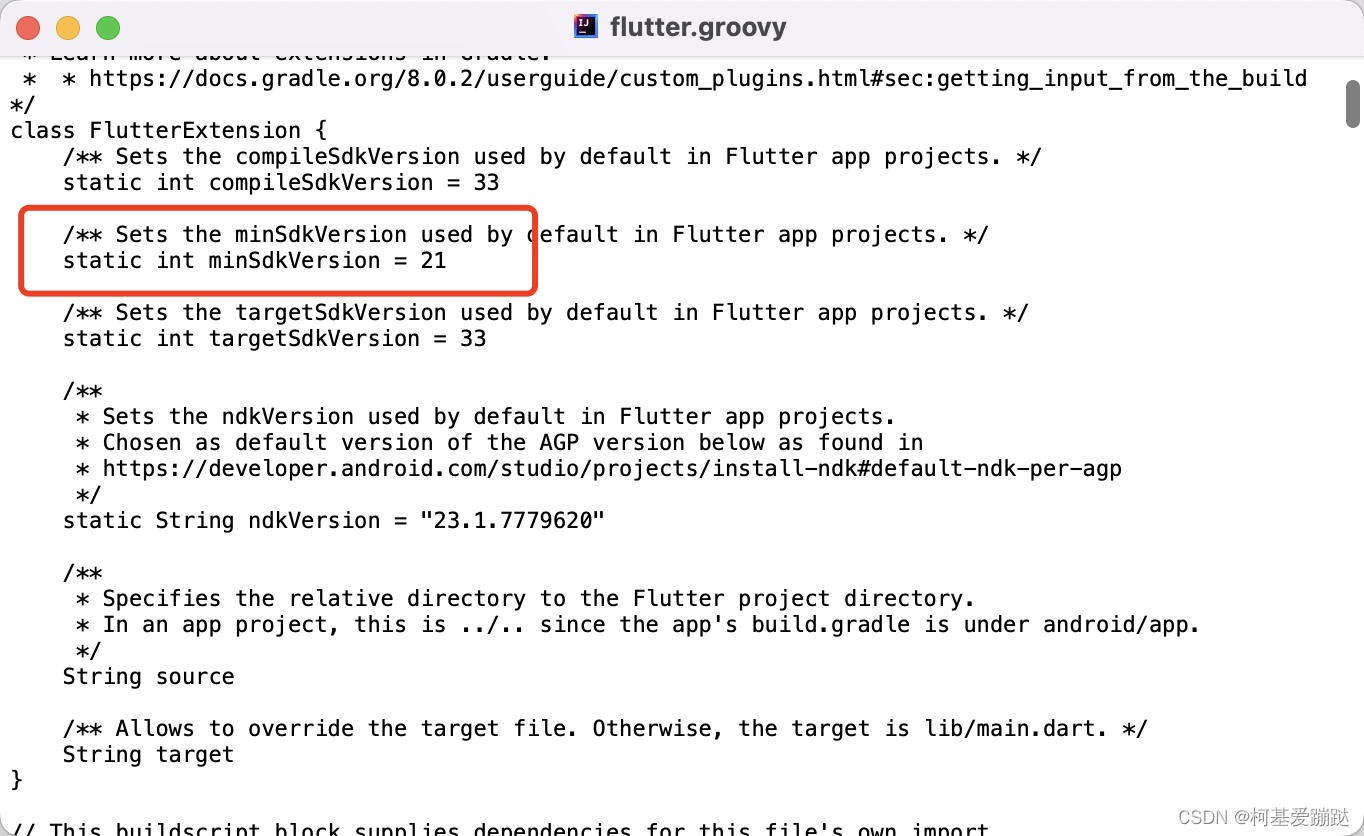
Flutter flutter.minSdkVersion的实际文件位置
Flutter 项目的Android相关版本号配置: flutter.minSdkVersion 的版本号配置文件实际路径: …/flutter_sdk/packages/flutter_tools/gradle/src/main/groovy/flutter.groovy Flutter版本号如下: bzbMacBook-Pro ccsmec % flutter --version …...
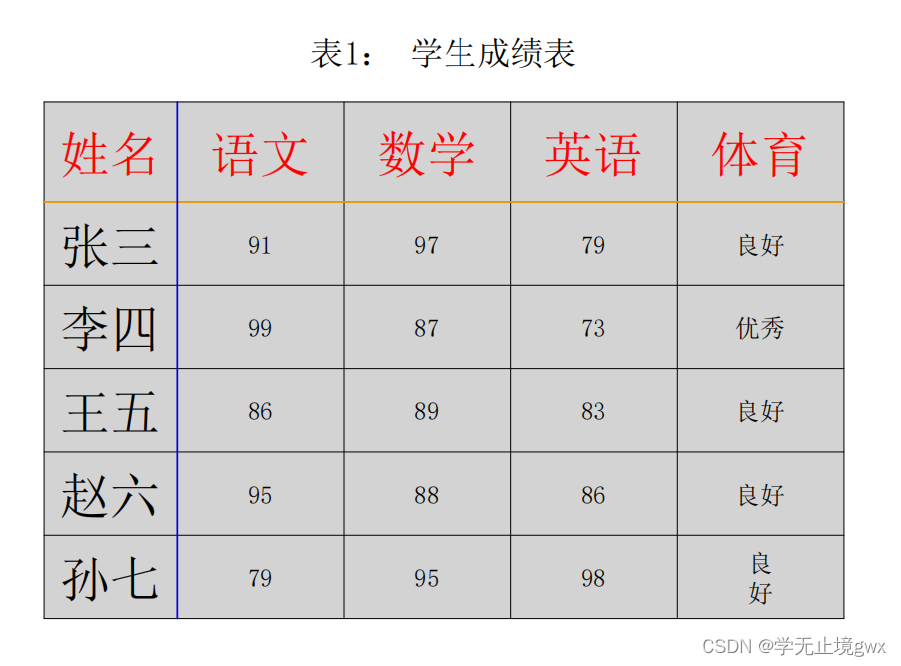
python生成PDF报告
前言 最近接到了一个需求-将项目下的样本信息汇总并以PDF的形式展示出来,第一次接到这种PDF的操作的功能,还是有点慌的,还好找到了reportlab这个包,可以定制化向PDF写内容! 让我们由简入深进行讲解 一、reportlab是…...
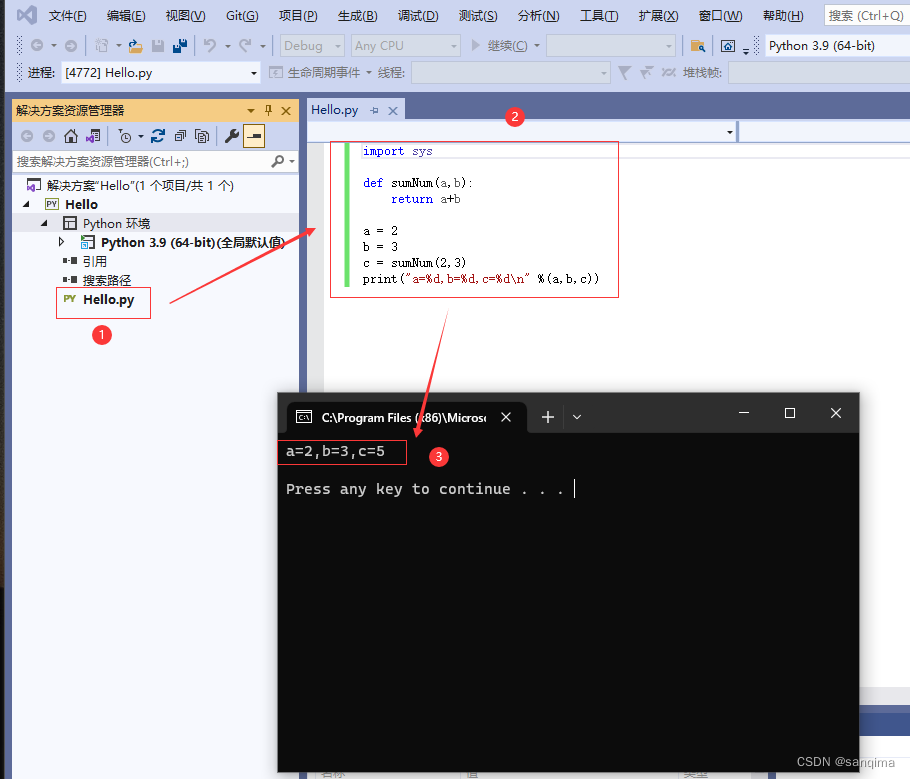
在visual studio里安装Python并创建python工程
在2009年,云计算开始发力,Python、R、Go这些天然处理批量计算的语言也迅猛发展。微软在2010年,把Python当成一个语言包插件,集成到了visual studio 2010里。在"云优先,移动优先"的战略下,于2015年…...
试用 6 -- 从简单到复杂)
AIGC(生成式AI)试用 6 -- 从简单到复杂
从简单到复杂,这样的一个用例该如何设计? 之前浅尝试用,每次尝试也都是由浅至深、由简单到复杂。 一点点的“喂”给生成式AI主题,以测试和验证生成式AI的反馈。 AIGC(生成式AI)试用 1 -- 基本文本_Role…...
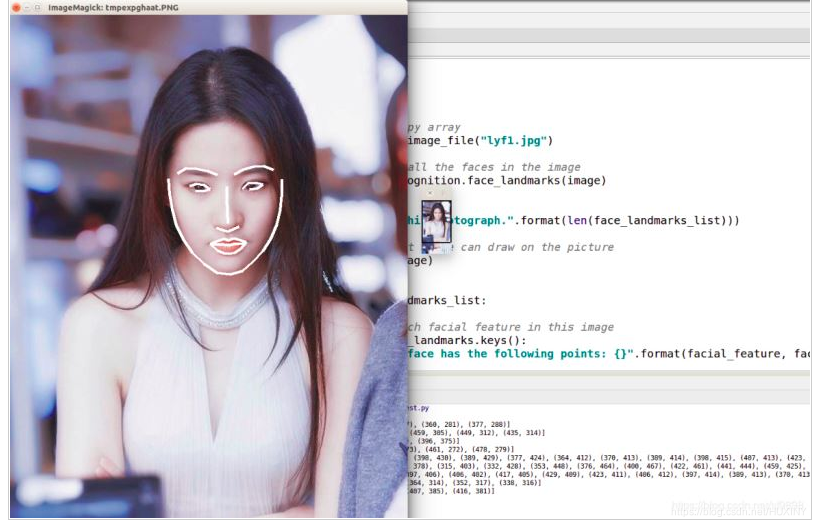
竞赛 基于深度学习的人脸识别系统
前言 🔥 优质竞赛项目系列,今天要分享的是 基于深度学习的人脸识别系统 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🧿 更多资料, 项目分享: https://gitee.com/dancheng-senior/…...

uniapp:APP开发,后台保活
前言: 在ios中,软件切换至后台、手机息屏,过了十来秒软件就会被系统挂起,APP内的任务就不能继续执行;在android中,默认情况下,软件在后台运行的时候,触发某些特定条件的情况下&…...
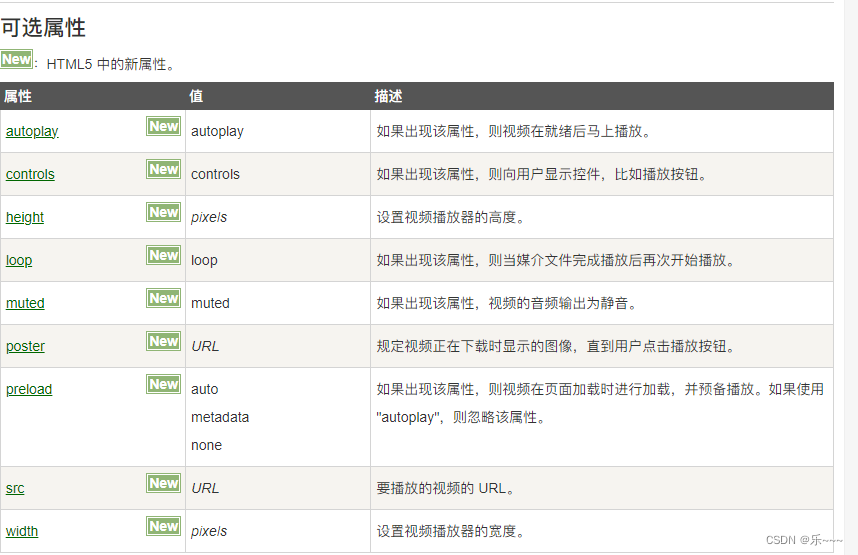
vue2 项目中嵌入视频
案例: 代码: <template><div class"schematicDiagramIndex"><el-container><el-aside width"20rem"> <!-- <h4 style"font-size: 18px">视频演示</h4>--><div styl…...

第二章 进程与线程 十二、进程同步与进程互斥
目录 一、进程同步 1、定义 二、进程互斥 1、定义 2、四个部分 3、原则 一、进程同步 1、定义 进程同步是指在多个进程之间协调执行顺序的一种机制,使得进程按照一定的顺序执行,以避免出现不一致的情况。常见的实现方式有信号量、管程、屏障等。…...
移植到任意平台)
Linux内核链表(list)移植到任意平台
一、前言 linux内核链表在include/linux/list.h文件中,内核中实现的链表比较简洁,实用性很强,因此想把它单独移植出来使用。 内核中的代码只能使用gnuc编译器编译,stdc编译器编译是会报错的,主要是因为typeof这个宏是…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...
