栈的简单应用(利用Stack进行四则混合运算)(JAVA)
目录
中缀表达式转后缀表达式
图解
代码实现过程:
完整代码:
利用后缀表达式求值:
完整代码:
首先我们得先了解逆波兰表达式。
中缀表达式转后缀表达式
所谓的中缀表达式其实就是我们平时写的例如:;而它的后缀表达式(也成为逆波兰表达式)为
;
后缀表达式:指的是不包含括号,运算符放在两个运算对象的后面,所有的计算按运算符出现的顺序,严格从左向右进行(不再考虑运算符的优先规则)。
我们如果要利用程序来进行四则混合运算最重要的就是将输入的中缀表达式转后缀表达式。
首先我们假设运算符中只有 加 减 乘 除 和 括号不然的话程序太复杂了(其实是我不会写【哭】)。
图解
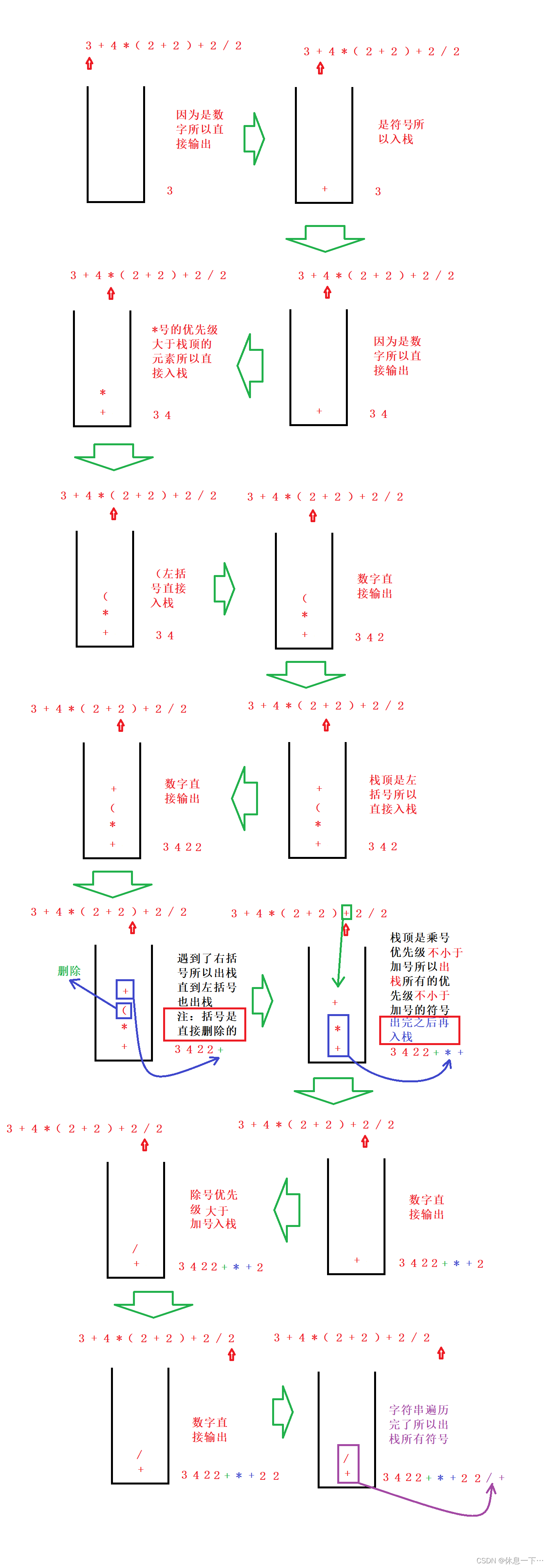
代码实现过程:
首先我们先写一个方法 返回值是动态字符串数组(为了后面好计算),形参为字符串类型(因为输入值不只有数字还有运算符)。这里会用到栈所以也定义一个栈。
public ArrayList<String> midChangeEng(String str) {//这里用动态数组就不用担心不够用ArrayList<String> ret = new ArrayList<String>();Stack<Character> stack = new Stack<>();}此时再创建一个新方法用来判断传入字符是不是运算符
public boolean isOperator(char s) {if (s == '+' || s == '-' || s == '*' || s == '/' || s == '(' || s == ')') {return true;}return false;}我们再利用运算符再ASCII码中的位置,创建一个数组用来表示它们的优先级


int[] able = {1,0,0,0,0,1};//分别代表 * + (null) - (null) / 的优先级 利用循环遍历字符串
//遍历字符串for (int i = 0; i < str.length(); i++) {char a = str.charAt(i);String tmp = "";//用来暂时存储出栈的数字if (isOperator(a)) {//是操作数}else{//如果是数字就放到ret中}}return ret;对操作数的操作 ,可是此段代码中重复代码过多,所以可以将其封装成一个方法。
if (isOperator(a)) {//是操作数switch (a) {case '+'://判断如果优先级不大于栈顶的元素那么就先出栈在入栈if(!stack.isEmpty()) {//出栈while(!stack.isEmpty() && stack.peek() != '(' && able[(int)stack.peek() - 42] >= able[(int)a-42]) {String b = "";b += stack.pop();ret.add(b);}}stack.push(a);break;case '-':if(!stack.isEmpty()) {//出栈while(!stack.isEmpty() && stack.peek() != '(' && able[(int)stack.peek() - 42] >= able[(int)a-42]) {String b = "";b += stack.pop();ret.add(b);}}stack.push(a);break;case '*':if(!stack.isEmpty()) {//出栈while(!stack.isEmpty() && stack.peek() != '(' && able[(int)stack.peek() - 42] >= able[(int)a-42]) {String b = "";b += stack.pop();ret.add(b);}}stack.push(a);break;case '/':if(!stack.isEmpty()) {//出栈while(!stack.isEmpty() && stack.peek() != '(' && able[(int)stack.peek() - 42] >= able[(int)a-42]) {String b = "";b += stack.pop();ret.add(b);}}stack.push(a);break;case '(':stack.push(a);break;case ')':while(!stack.isEmpty() && stack.peek() != '(') {String b = "";b += stack.pop();ret.add(b);}stack.pop();//删除‘(’break;}}如果是数字就进行以下操作
else{//如果是数字就放到ret中String tmp = "";while(i < str.length() && !isOperator(str.charAt(i))) {//数字有可能是多位的tmp += str.charAt(i);i++;}i--;ret.add(tmp);}再出函数之前要先将栈里面的全部导出来
//将栈里面剩余的全部出栈while(!stack.isEmpty()) {String b = "";b += stack.pop();ret.add(b);}return ret;完整代码:
public static ArrayList<String> midChangeEng(String str) {//这里用动态数组就不用担心不够用ArrayList<String> ret = new ArrayList<String>();Stack<Character> stack = new Stack<>();int[] able = {1,0,0,0,0,1};//分别代表 * + (null) - (null) / 的优先级//遍历字符串for (int i = 0; i < str.length(); i++) {char a = str.charAt(i);if (isOperator(a)) {//是操作数switch (a) {case '+'://判断如果优先级不大于栈顶的元素那么就先出栈在入栈abcd(ret, stack, able, a);break;case '-':abcd(ret, stack, able, a);break;case '*':abcd(ret, stack, able, a);break;case '/':abcd(ret, stack, able, a);break;case '(':stack.push(a);break;case ')':while(!stack.isEmpty() && stack.peek() != '(') {String b = "";b += stack.pop();ret.add(b);}stack.pop();//删除‘(’break;}}else{//如果是数字就放到ret中String tmp = "";while(i < str.length() && !isOperator(str.charAt(i))) {//数字有可能是多位的tmp += str.charAt(i);i++;}i--;ret.add(tmp);}}//将栈里面剩余的全部出栈while(!stack.isEmpty()) {String b = "";b += stack.pop();ret.add(b);}return ret;}

利用后缀表达式求值:
这部分比较简单所以就直接展示了
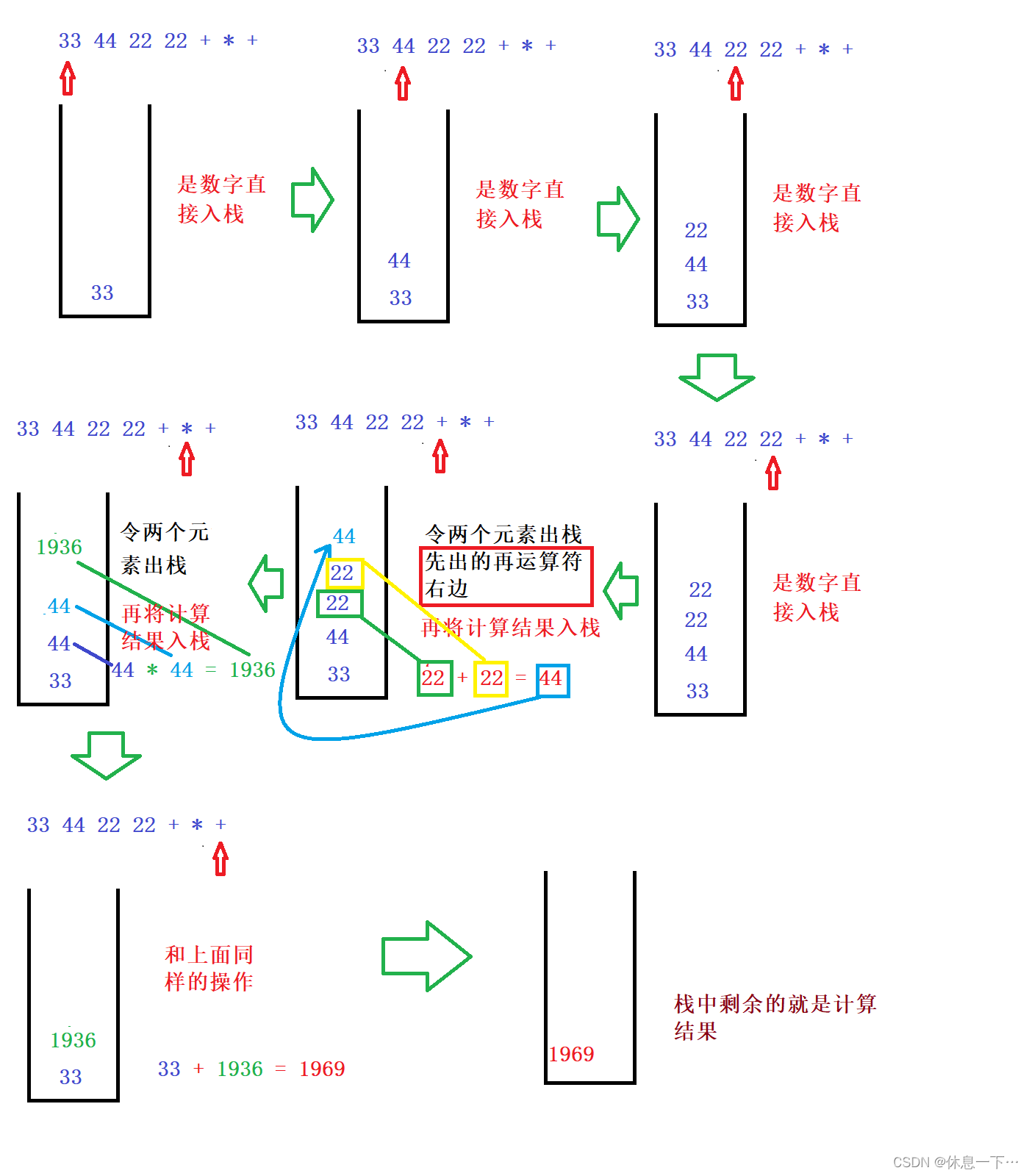
完整代码:
public int evalRPN(String[] tokens) {Stack<Integer> stack = new Stack<>();for (int i = 0; i < tokens.length; i++) {if (isOperator(tokens[i])) {int num2 = stack.pop();int num1 = stack.pop();switch(tokens[i].charAt(0)) {case '+':stack.push(num1 + num2);break;case '-':stack.push(num1 - num2);break;case '*':stack.push(num1 * num2);break;case '/':stack.push(num1 / num2);break;}}else {stack.push(Integer.parseInt(tokens[i]));}}return stack.pop();}public boolean isOperator(String str) {if (str.length() != 1) {return false;}if (str.charAt(0) == '+' || str.charAt(0) == '-' || str.charAt(0) == '*' || str.charAt(0) == '/') {return true;}return false;}相关文章:

栈的简单应用(利用Stack进行四则混合运算)(JAVA)
目录 中缀表达式转后缀表达式 图解 代码实现过程: 完整代码: 利用后缀表达式求值: 完整代码: 首先我们得先了解逆波兰表达式。 中缀表达式转后缀表达式 所谓的中缀表达式其实就是我们平时写的例如:࿱…...

Python---异常
捕获全部异常 语法: try: 可能发生的错误代码 except: 如果出现异常执行的代码 例子: try:open("test2.txt", "r", encoding"UTF-8") except:print("出现异常,文件不存在,换个模式打…...

视频编解码器H.264和H265有什么区别?
对于大型视频文件来说,视频编解码器至关重要,它可以将文件压缩为较小的尺寸,从而可以更轻松地存储和加快传输速度。而两种最常用的编解码器是H.264和H.265,那么它们两者之间有什么区别,哪一个更好呢? 1. 什…...
网络安全进阶学习第十六课——业务逻辑漏洞介绍
文章目录 一、什么是业务逻辑二、业务逻辑漏洞的成因三、逻辑漏洞的重要性四、业务逻辑漏洞分类五、业务逻辑漏洞——业务授权安全1、未授权访问2、越权访问1) 平行越权(水平越权是指相同权限的不同用户可以互相访问)2) 垂直越权(垂直越权是指…...

华为OD:跳房子I
题目描述 跳房子,也叫跳飞机,是一种世界性的儿童游戏。 游戏参与者需要分多个回合按顺序跳到第1格直到房子的最后一格 跳房子的过程中,可以向前跳,也可以向后跳。 假设房子的总格数是count,小红每回合可能连续跳的…...
C语言自定义类型详解(1)结构体知识汇总
本篇概要 本篇主要讲述C语言结构体的相关知识,包括结构体的基本声明,结构体的匿名结构,结构体的自引用,结构体变量的定义和初始化以及结构体的内存对齐等相关知识。 文章目录 本篇概要1.结构体1.1结构体的基本声明1.2结构体的特殊…...
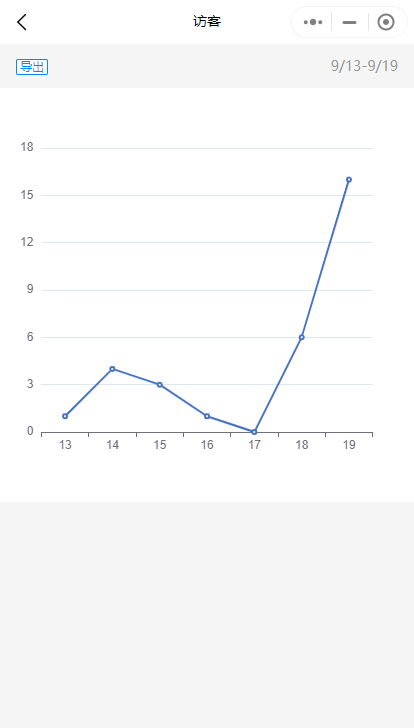
小程序中如何查看会员的访问记录
在小程序中,我们可以通过如下方式来查看会员的访问记录。下面是具体的操作流程: 1. 找到指定的会员卡。在管理员后台->会员管理处,找到需要查看访客记录的会员卡。也支持对会员卡按卡号、手机号和等级进行搜索。 2. 查看会员卡详情。点…...

SpringCloud Alibaba - Sentinel
接上文SpringCloud Alibaba - Nacos 1.Sentinel 流量防卫兵 1.1 安装与部署 和Nacos一样,它是独立安装和部署的,下载地址https://github.com/alibaba/Sentinel/releases 下载后的jar放到目录 然后配置 启动并访问,用户名密码都是 sentinel 此时就…...

内存泄漏,内存溢出,抽象类和接口,netstat、ping、ifconfig的区别
持续学习是我们必备的技能之一,保持与时俱进,保持行业的敏感度,关注行业发展趋势,了解新技术,加强自己的认知,积极的应对变化 内存泄漏 memory leak 是指程序在申请内存后,无法释放已申请的内…...

TensorFlow安装 ,在原本的虚拟环境下配置Tensorflow.
1.TensorFlow安装 ,在原本的虚拟环境下配置Tensorflowh和pytorch 2.我首先在anaconda的环境下创建了一个tensorflow文件夹 如何先进入D盘,再进入tensorflow文件夹的目录D:cd D:\Anaconda\TensorFlowSoftWarepip install tensorflow如图所示报错解决方法 …...

如何使用HTML, CSS和JavaScript开发一个浏览器打字游戏:从零到一的详细步骤与完整代码教程
第一部分:游戏概述与HTML结构 1. 游戏概述 打字游戏是一个训练用户打字速度和准确性的游戏。用户将会看到一个随机的单词或句子,并在限定时间内尽快准确地键入该单词或句子。每次正确输入,玩家得分,每次输入错误,扣分。这个游戏不仅能够增加用户的打字速度,还可以为学习…...
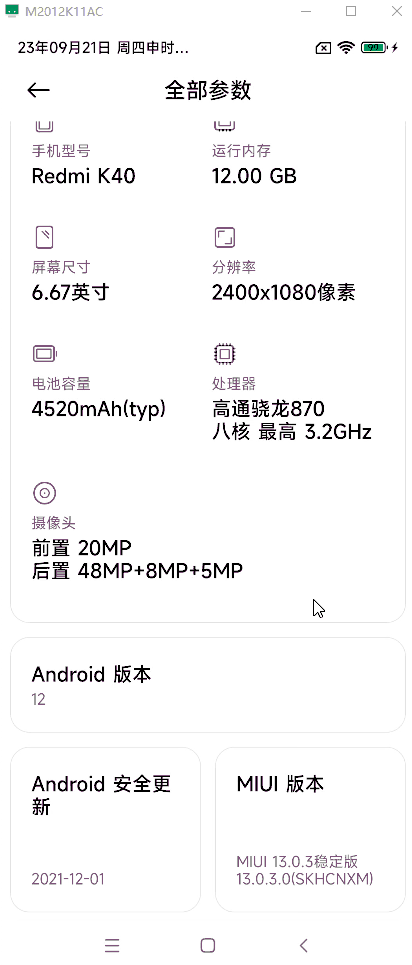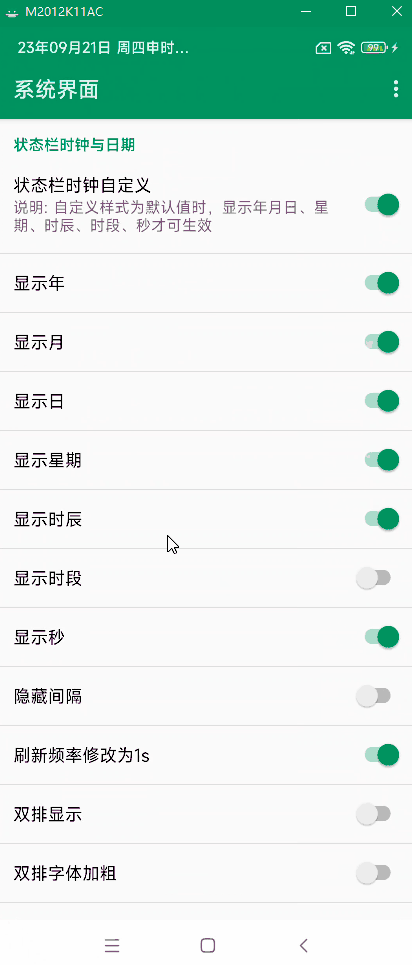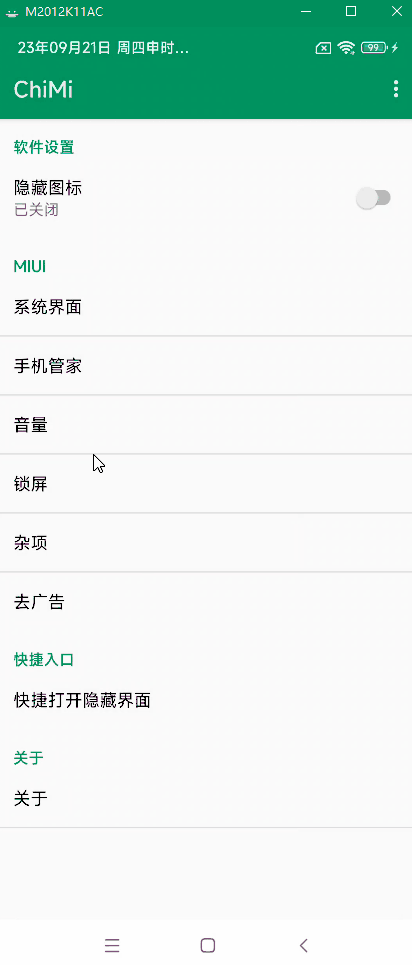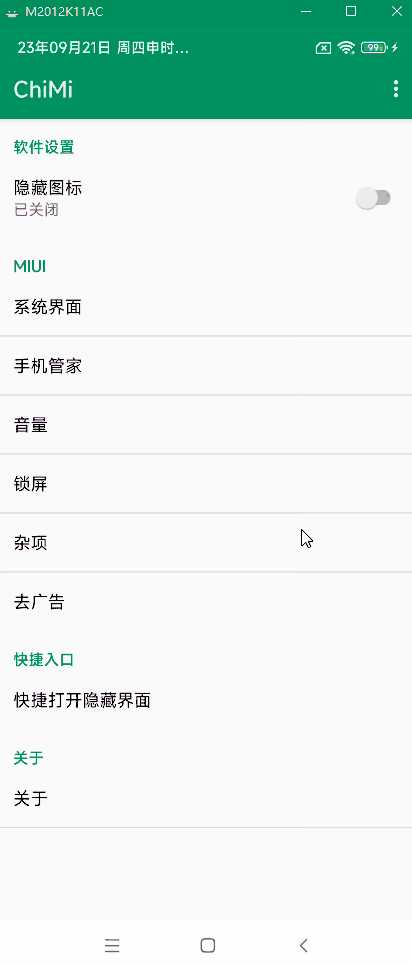
安卓玩机搞机----不用刷第三方官改固件即可享受“高级设置”的操作 ChiMi安装使用步骤
很多玩友特别喜欢第三方作者修改的带有高级设置的官改包。因为他可以随意修改系统里面的有关设置选项。包括但不限于修改状态栏 显示日期 秒等等的操作。 第三方带高级设置的官改 一般官改带高级设置的类似与 今天给大家分享下不用刷这些官改包即可享受高级设置的操作。 红米…...
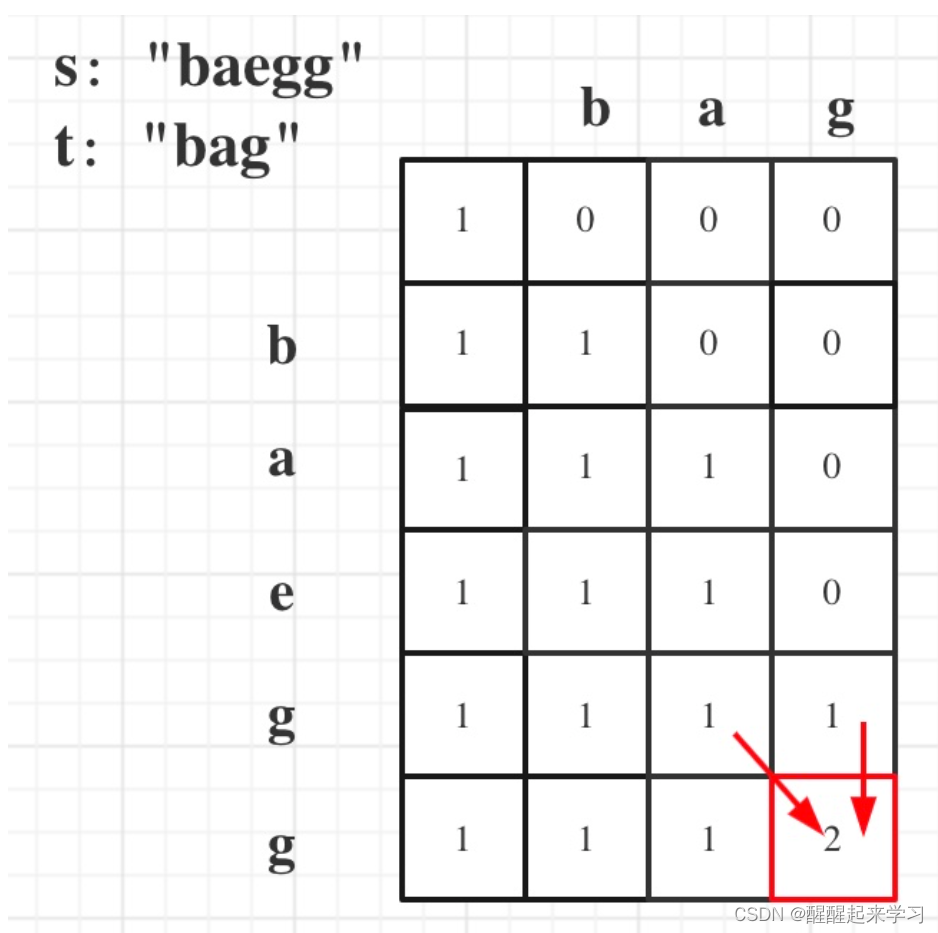
代码随想录|392.判断子序列,115.不同的子序列(需要二刷)
392.判断子序列 先用双指针做 class Solution {public boolean isSubsequence(String s, String t) {//双指针int ms.length();int nt.length();int slow0;int i0;int j0;while(i<m&&j<n){if(s.charAt(i)t.charAt(j)){i;System.out.println(i);}j;}return im?…...
Linux——文件系统
✅<1>主页::我的代码爱吃辣 📃<2>知识讲解:Linux——文件系统 ☂️<3>开发环境:Centos7 💬<4>前言:上期我们了解了文件在内存中得组织方式,那么文件在磁盘中…...

《动手学深度学习 Pytorch版》 7.3 网络中的网络(NiN)
LeNet、AlexNet和VGG的设计模式都是先用卷积层与汇聚层提取特征,然后用全连接层对特征进行处理。 AlexNet和VGG对LeNet的改进主要在于扩大和加深这两个模块。网络中的网络(NiN)则是在每个像素的通道上分别使用多层感知机。 import torch fr…...

古代有没有电子元器件?
手机,电脑,电视等等电子产品,无时无刻充斥在我们的生活中,如果有一天突然没有了这些功能多样的电子产品,估计大部分人都会一时之间难以适应。 这就好比正在上网,结果突然被人断了网,导致无网络连…...

log4j2或者logback配置模版实现灵活输出服务名
介绍 在我们使用log4j2或者logback打印日志时,输出的内容中通常是一定要加上服务名的。以log4j2为例: <!--输出控制台的配置--> <Console name"Console" target"SYSTEM_OUT"><!-- 输出日志的格式 --><Patter…...

使用HTTP爬虫ip中的常见误区与解决方法
在如今的互联网时代,为了保障个人隐私和实现匿名浏览,许多人选择使用HTTP爬虫ip。然而,由于缺乏了解和使用经验,常常会出现一些误区。本文将为大家介绍使用HTTP爬虫ip过程中常见的误区,并提供相应的解决方法࿰…...
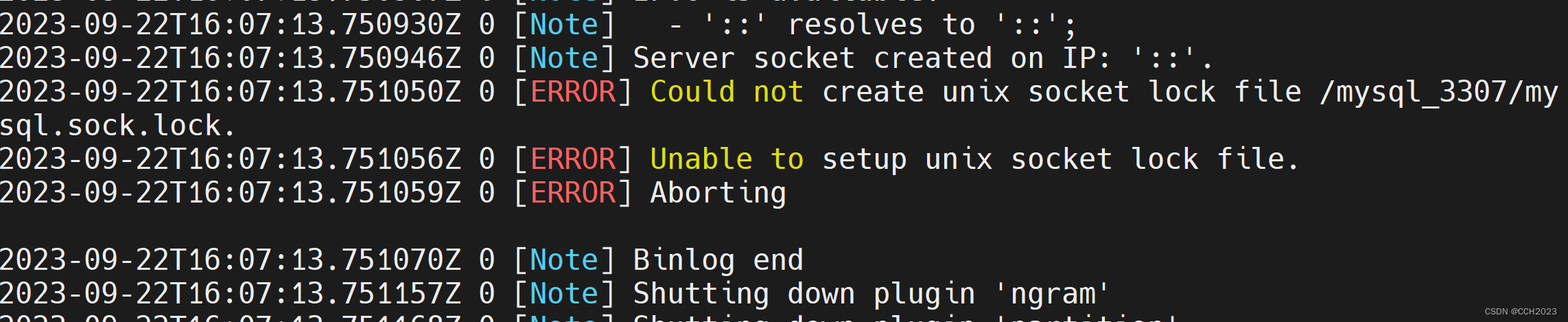
MySQL学习笔记3
MySQL的源码编译安装: 1、参考MySQL的源码安装官方文档: 2、源码安装定制选项: 3、源码安装三部曲:配置、编译、安装。 4、软件安装包: mysql-boost-5.7.43.tar.gz 5、安装需求: 安装需求具体配置安装目…...

快速掌握ES6
什么是ES6 ES6(ECMAScript 6),也被称为ES2015,是JavaScript的第六个版本,于2015年发布。ES6引入了许多新的语法和功能,旨在提高JavaScript的开发效率和代码质量。 ES6的一些主要特性和改进包括࿱…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...
