进入数据结构的世界
数据结构和算法的概述
- 一、什么是数据结构
- 二、什么是算法
- 三、如何去学习数据结构和算法
- 四、算法的时间复杂度和空间复杂度
- 4.1 算法效率
- 4.2 大O的渐进表示法
- 4.3 时间复杂度
- 4.4 空间复杂度
- 4.5 常见复杂度对比
一、什么是数据结构
数据结构是计算机存储、组织数据的方式。(相互之间存在一种或多种特定关系的数据元素的集合)
二、什么是算法
算法就是一系列的计算步骤,用来吧输入数据转换成输出结果。(算法就是有良好的计算过程,把一个或一组的值输入,并产出一个或一组的值输出)
三、如何去学习数据结构和算法
现在的公司对学生的代码能力越来越高,数据结构和算法的题目越来越难。算法的能力在短期内是不能够快速提升的,需要进行算法训练的积累。校招的时候,笔试很难,为了能够找到工作,还需要对数据结构和算法早早的准备,多去训练算法能力。
数据结构和算法对于初学者来说很难。但 是,古话说的好,世上无难事,只怕有心人。不管数据结构和算法有多难,我们都要硬着头皮去学。我相信,只要多学多练,学习数据结构和算法就会越来越简单。
四、算法的时间复杂度和空间复杂度
时间和空间这两个维度能够衡量算法的好坏,
4.1 算法效率
算法在编写成可执行程序后,运行程序需要耗费空间资源和时间资源。因此,衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,这就是时间复杂度和空间复杂度。
时间复杂度主要是衡量算法的运行快慢,而空间复杂度主要是衡量一个算法运行时所需要的额外空间。(计算机发展的早期,计算机存储的容量很小,我们对空间复杂度很在乎。但是经过计算机行业的快速发展,计算机存储的容量已经达到了很高的地步。所以我们今天已经不需要特别在关注算法的空间复杂度)
4.2 大O的渐进表示法
大O符号(Big O notation):用于描述函数渐进行为的数学符号
大O的渐进表示法的推导方法:
1、用常数1取代运行时间中所以的加法常数。
2、在运行次数函数中,只保留最高阶项。
3、如果最高价项存在且不是1,则去除与这个项相乘的常数,得到的结果就是大O阶。
算法的时间复杂度存在最好、平均和最坏情况:
最好情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最坏情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N的数组中搜索一个数据x
最好情况:1次找到
平均情况:N/2次找到
最坏情况:N次找到
实际中,我们关注的都是算法的最坏情况。所以,数组中搜索数据的时间复杂度为O(N)
4.3 时间复杂度
时间复杂度的定义:
一个算法执行所消耗的时间,从理论上说,是不能够算出来得,只有把程序放在机器上跑,才能够知道消耗的时间。一个算法所花费的时间与其中语句的执行次数成正比,算法的基本操作的执行次数,就是算法的时间复杂度。
案例1:
找到基本语句与问题规模n的数学表达式,算出该算法的时间复杂度。
//计算++count语句执行的次数
#include <stdio.h>
int main()
{int n = 0;scanf("%d", &n);int count = 0;for (int i = 0; i < n; i++){for (int j = 0; j < n; j++)++count;}for (int i = 0; i < 2 * n; i++){++count;}int m = 10;while (m--){++count;}printf("%d\n", count);return 0;
}
基本操作次数:
F(n)=n^2+2*n+10
- n=10 F(n)=130
- n=100 F(n)=10210
- n=1000 F(n)=1002010
用大O的渐进表示法,时间复杂度为O(N^2)
- n=10 F(n)=100
- n=100 F(n)=10000
- n=1000 F(n)=1000000
实际中我们计算时间复杂度时,并不一定计算精准的时间复杂度,而只需要大概执行次数,这里我们使用大O的渐进表示法。
通过上面我们可以发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
案例2:
计算Fun2的时间复杂度
void Fun2()
{int N;scanf("%d", &N);int count = 0;for (int i = 0; i < 2 * N; i++){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
Fun2的时间复杂度为:
F(N)=2*N+10
大O的渐进表示法:时间复杂度为O(N)
案例3:
//计算Fun3的时间复杂度
void Fun3()
{int N, M;scanf("%d%d", &N, &M);int count = 0;for (int i = 0; i < N; i++){++count;}for (int j = 0; j < M; j++){++count;}printf("%d\n", count);
}
Fun2的时间复杂度为:
F(N)=N+M
大O的渐进表示法:时间复杂度为O(N)
案例4:
//二分查找的思想
void Fun4()
{int m = 0;int arr[10] = { 1,2,4,6,8,11,55,66,77,88};int n;printf("请输入要查找的数:\n");scanf("%d", &n);int begin = 0;int end = 9;while (begin <= end){int mid = begin + (end - begin)/2;if (arr[mid] < n)begin = mid + 1;else if (arr[mid] > n)end = mid - 1;else{printf("找到了\n");printf("%d", arr[mid]);m = 1;break;}}if(m==0)printf("没找到\n");
}
区间数据个数:
N
N/2
N/2/2
…………
N/2/2/2……/2=1
最坏的情况,查找区间缩放只剩一个值时,就是坏得,
假设查找x次,2^x=N,所以x=logN。
大O的渐进表示法:时间复杂度为O(logN).
案例5:
//斐波那契递归的复杂度
#include <stdio.h>
int Fun5(size_t n)
{if (n < 3)return 1;return Fun5(n - 2) + Fun5(n - 1);}
int main()
{int n = 7;int sum=Fun5(n);printf("%d\n", sum);return 0;
}
打印结果:
递归展开图:
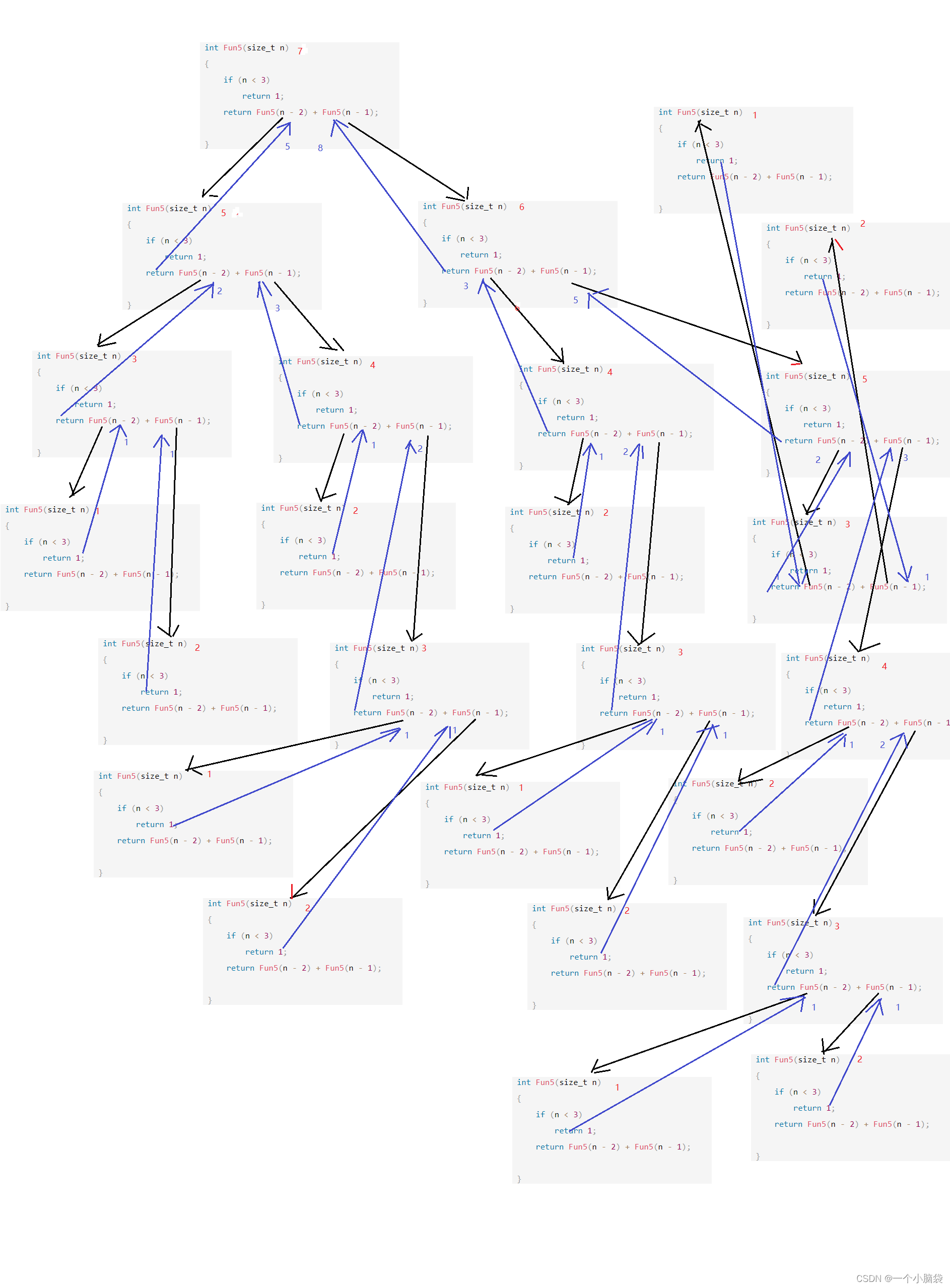
1次(2^ 0)
2次(2^ 1)
4次(2^ 2)
8次(2^ 3)
……
2^(N-1)次
通过函数递归图分析基本操作递归了2 ^N-1次,
大O的渐进表示法:时间复杂度为O (2 ^N)。
4.4 空间复杂度
空间复杂度的定义:
一个算法在运行过程中临时占用存储空间大小的量度。(空间复杂度算的是变量的个数)
注意:
函数运行时所需要的栈空间(存储函数、局部变量、一些寄存器信息等)在编译期间就已经确定好了,因此,空间复杂度主要就是函数在运行的时候申请的额外空间来确定的。
案例1:
//计算BubbleSort函数的空间复杂度
void BubbleSort(int* a, int n)
{assert(a);for (int end = n; end > 0; end--){int exchange = 0;for (int i = 1; i < n; i++){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}//不需要循环了if (exchange == 0)break;}
}
可以看出使用了常数个额外空间,所以空间复杂度为O(1)
案例2:
//看返回斐波那契数列的前n项,计算Fibonac的空间复杂度
int* Fibonac(int n)
{if (n == 0)return NULL;int* fibar = (int*)malloc(sizeof(int) * (n + 1));fibar[0] = 0;fibar[1] = 1;for (int i = 2; i <= n; i++){fibar[i] = fibar[i - 1] + fibar[i - 2];}return fibar[i];
}
动态开辟了n+1个空间,大O的渐进表示法为O(N);
4.5 常见复杂度对比
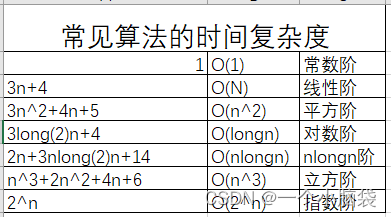
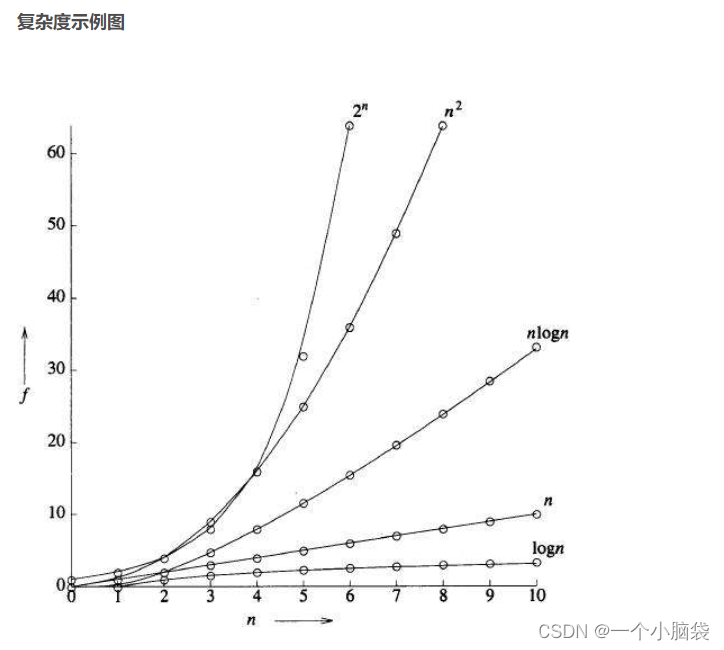
相关文章:

进入数据结构的世界
数据结构和算法的概述 一、什么是数据结构二、什么是算法三、如何去学习数据结构和算法四、算法的时间复杂度和空间复杂度4.1 算法效率4.2 大O的渐进表示法4.3 时间复杂度4.4 空间复杂度4.5 常见复杂度对比 一、什么是数据结构 数据结构是计算机存储、组织数据的方式。&#x…...

stm32之看门狗
STM32 有两个看门狗,独立看门狗和窗口看门狗,独立看门狗又称宠物狗,窗 口看门狗又称警犬。可用来检测和解决由软件错误引起的故障。两个看门狗的原理都是当计数器达到给定的超时值时,产生系统复位,对于窗口型看门狗同…...
纤维蛋白单体(FM)介绍
纤维蛋白单体(FM)是血栓形成的早期产物,是纤维蛋白原(Fibrinogen,Fbg)在凝血酶(Thrombin)的作用下,脱掉肽A(Fibrinopeptide A,Fp A)与…...

知识图谱实战导论:从什么是KG到LLM与KG/DB的结合实战
前言 本文侧重讲解: 什么是知识图谱LLM与langchain/数据库/知识图谱的结合应用 比如,虽说基于知识图谱的问答 早在2019年之前就有很多研究了,但谁会想到今年KBQA因为LLM如此突飞猛进呢 第一部分 知识图谱入门导论 //待更.. 第二部分 LLM与…...

第5章 会话与会话技术
第5章 会话与会话技术 一. 单选题(共5题,50分)二. 判断题(共5题,50分) 一. 单选题(共5题,50分) (单选题) 阅读下面代码: Book book BookDB.getBook(id)…...
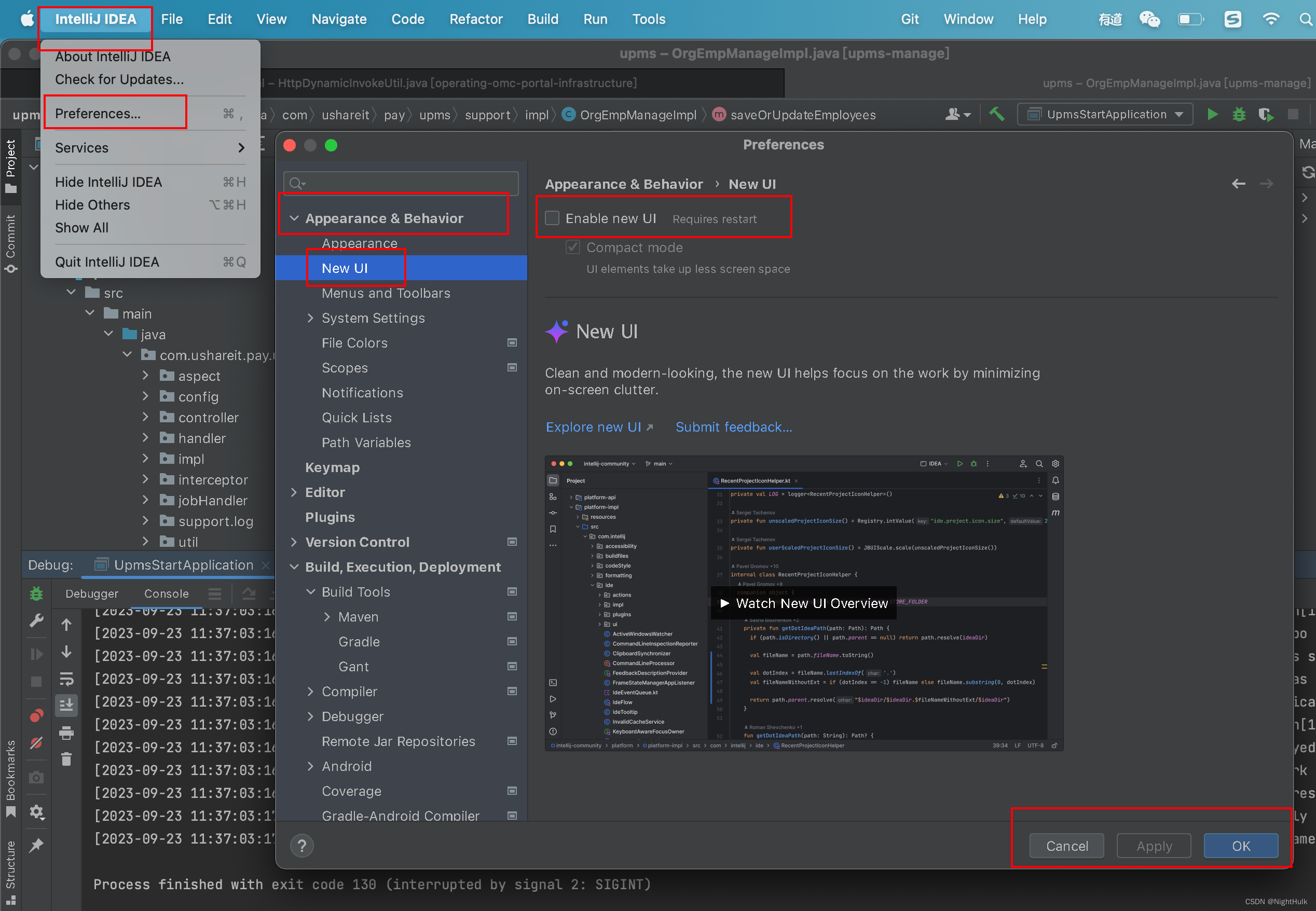
IDEA2023新UI回退老UI
idea2023年发布了新UI,如下所示 但是用起来真心不好用,各种位置也是错乱,用下面方法可以回退老UI...
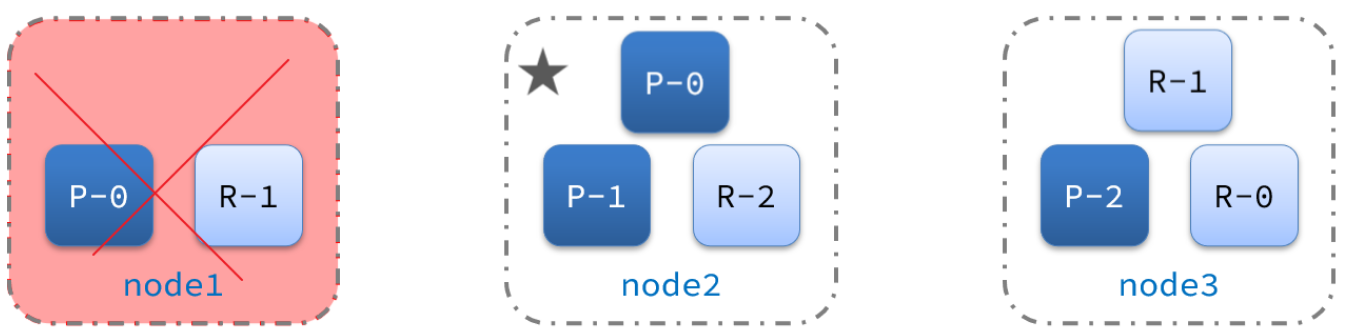
ElasticSearch(三)
1.数据聚合 聚合(aggregations)可以让我们极其方便的实现对数据的统计、分析、运算。例如: 什么品牌的手机最受欢迎? 这些手机的平均价格、最高价格、最低价格? 这些手机每月的销售情况如何? 实现这些…...

【LinkedHashMap】146. LRU 缓存
146. LRU 缓存 解题思路 与普通的 HashMap 不同,LinkedHashMap 会保持元素的有序性。这可以在某些情况下提供更可预测的迭代顺序直接获取元素 因为使用到该元素 将该元素重新放入队尾 表示最近使用该元素写入元素,首先如果该元素原来存在 那么需要将ke…...
Opencv-python去图标与水印方案实践
RGB色彩模式是工业界的一种颜色标准,是通过对红(R)、绿(G)、蓝(B)三个颜色通道的变化以及它们相互之间的叠加来得到各式各样的颜色的,RGB即是代表红、绿、蓝三个通道的颜色ÿ…...

自己写过比较蠢的代码:从失败中学习的经验
文章目录 引言1. 代码没有注释2. 长函数和复杂逻辑3. 不恰当的变量名4. 重复的代码5. 不适当的异常处理6. 硬编码的敏感信息7. 没有单元测试结论 🎉 自己写过比较蠢的代码:从失败中学习的经验 ☆* o(≧▽≦)o *☆嗨~我是IT陈寒🍹✨博客主页&a…...
)
C语言 cortex-A7核 点LED灯 (附 汇编实现、使用C语言 循环实现、使用C语言 封装函数实现【重要、常用】)
1 汇编实现 text global _start start: ************** LED1点灯 ---> PE10 **************/ ************** RCC章节初始化 **************/ CC_INIT:1.使能GPIOE组控制器,通过RCC_MP_AHB4ENSETR寄存器设置GPIOE组使能0x50000A28[4] 1ldr r0,0x50000A28 准…...
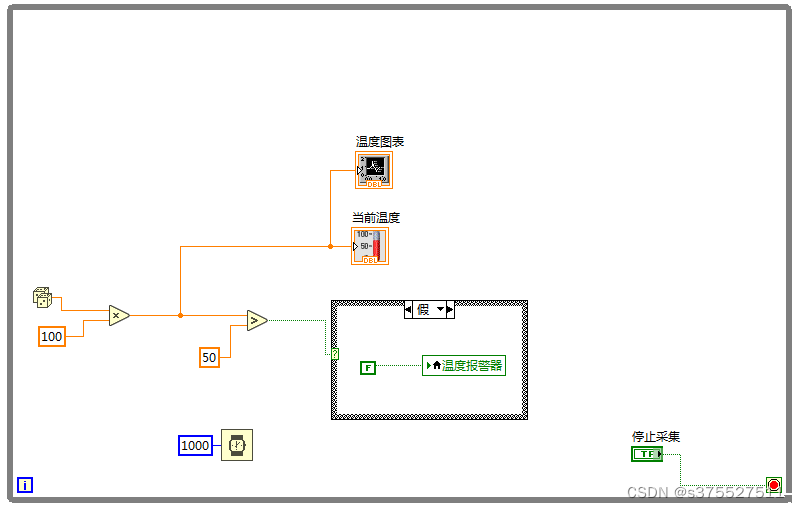
LABVIEW 实战案例1--温度报警系统
图1 温度报警系统前面板 图2 温度报警系统后面板...

【力扣】292. Nim 游戏
题目描述 你和你的朋友,两个人一起玩 Nim 游戏: 桌子上有一堆石头。你们轮流进行自己的回合, 你作为先手 。每一回合,轮到的人拿掉 1 - 3 块石头。拿掉最后一块石头的人就是获胜者。 假设你们每一步都是最优解。请编写一个函数…...
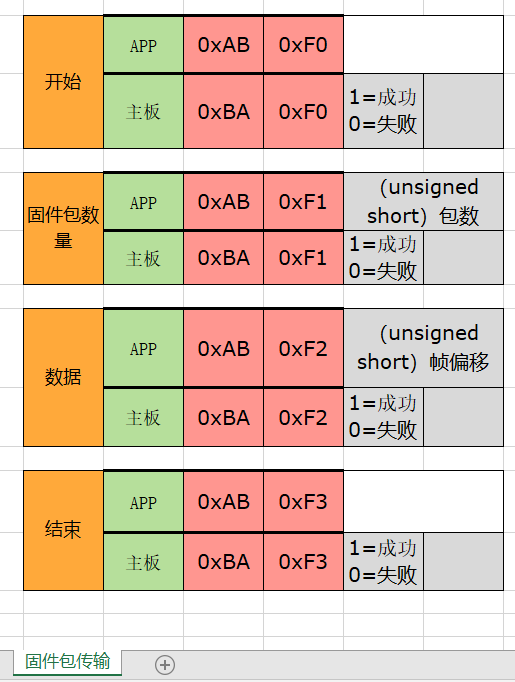
IAP固件升级分几步?(Qt上位机、)
前言 这周一直想做一个IAP固件升级的上位机,然后把升级流程全都搞懂 有纰漏请指出,转载请说明。 学习交流请发邮件 1280253714qq.com IAP原理 IAP的原理我就不多赘述了,这里贴上几位大佬的文章 STM32CubeIDE IAP原理讲解,及U…...
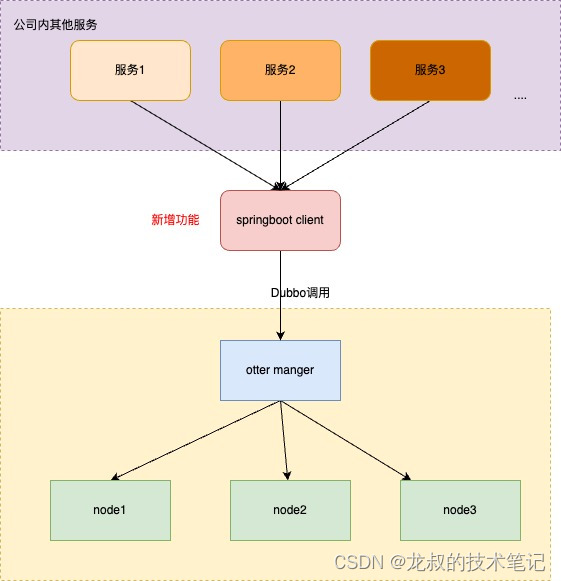
Otter改造 增加springboot模块和HTTP调用功能
环境搭建 & 打包 环境搭建: 进入 $otter_home/lib 目录执行:bash install.sh 打包: 进入$otter_home目录执行:mvn clean install -Dmaven.test.skip -Denvrelease发布包位置:$otter_home/target 项目背景 阿里…...
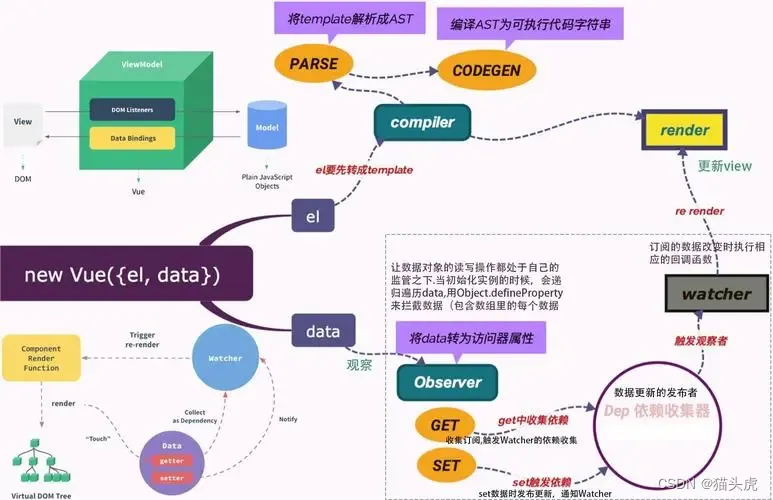
Vue.js vs React:哪一个更适合你的项目?
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...
Debian环境下搭建STM32开发环境
1. 安装交叉编译工具,解压gcc-arm-none-eabi-10.3-2021.10-x86_64-linux.tar.bz2,并且把交叉编译环境添加到path路径。 2.安装下载工具驱动和下载工具 # 安装下载工具openocd sudo apt -y install openocd 3.下载测试 sudo openocd -f cmsis-dap.cfg -…...

如何防止商业秘密泄露(洞察眼MIT系统商业机密防泄密解决方案)
在当今的商业环境中,保护公司的商业秘密是至关重要的。商业秘密可能包括独特的业务流程、客户列表、研发成果、市场策略等,这些都是公司的核心竞争力。一旦这些信息被泄露,可能会对公司的生存和发展产生重大影响。本文将探讨如何通过使用洞察…...

题目 1062: 二级C语言-公约公倍
输入两个正整数m和n,求其最大公约数和最小公倍数。样例输入 2 3样例输出 1 6 这题一知半解的, 最小公倍数两数の积/最大公约数; 最大公约数通过迭代法求得(见其下), 作为a,b两数有一个属为有一个为0为无效数据时 《-----a%b等…...
【Leetcode】148.排序链表
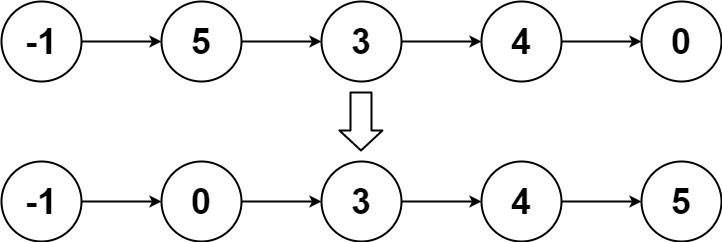
一、题目 1、题目描述 给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。 示例1: 输入:head = [4,2,1,3] 输出:[1,2,3,4]示例2: 输入:head = [-1,5,3,4,0] 输出:[-1,0,3,4,5]示例3: 输入:head = [] 输出:[]提示: 链表中节点的数目在范围 [0, 5 …...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...
