【基础算法】关于高精度计算的问题【很高位数数据的加减乘除(相关代码用C++实现)】
文章目录
- 前言
- 1.高精度加法
- 2.高精度减法
- 3.高精度乘法
- 4.高精度除法
- 写在最后
前言
- 当我们在利用计算机进行一些计算时,可能会遇到这类问题 : 有些计算要求精度高,希望计算的数的位数可达几十位甚至几百位,虽然计算机的计算精度也算较高了,但因受到硬件的限制,往往达不到实际问题所要求的精度。
- 这时我们就可以通过程序设计来解决这类问题,
例如:创建一个数组,通过数组来存放高精度数的每一位上的数。
1.高精度加法
-
高精度加法是两个位数很大的两个数相加,例如
1234567898756432123456789 + 66666666666666666666666,这时候我们用平常的整型或者长整型去存放数据都是会溢出导致数据丢失的,所以此时我们可以用一个数组来存放每个数相对应位上的数(使用vector<int>, 假设这两个高精度数都大于0)。 -
不过在
C++中,直接将数输入到vector中是不可取的,并且加法是从两个数的低位开始相加一直加到高位,如果我们正常输入从高位开始存放的话,对于后面程序的设计是不方便的,所以这里我们用string来表示相应高精度数,然后将这个string从低位开始转化成整数依次存放在vector<int>当中,这样两个vector<int>就是我们想要的高精度数了。 -
同时我们需要另一个
vector<int>来存放相加后的数,由于相加数的存放是倒着的,所以最终的结果也是倒着存放在vector<int>中的,此时打印就需要从后面往前面打印输出。 -
加法不难,但要注意的是,如何在程序中表示进位,我们都知道,每一位数相加超过
10就要进位1,表示这一位的前一位要+1。3和5相加为8不用进位,而7和8相加要进位,最后在这一位留下来的是(7 + 8)- 10 = 5,在程序中可以表示为(7 + 8)% 10。而这个%10就显得格外重要了,如果你相加后的数小于10,它%10后,还是它本身,如果大于10,它就相当于去掉一个10,剩下的数就放进表示最终答案的vector<int>。 -
最后要注意的是,两个位上的数相加后的结果要
/=10,这是表示要除去这一位该留下的结果以及得到需要进的位,例如:7 + 8 = 15,在该位应该留下的最终结果为15 % 10 = 5,最后15 /= 10得到1,表示要进位1,该位的结果5除去。
下面是相关操作的代码实现:
#include <iostream>
#include <vector>using namespace std;vector<int> add(vector<int>& A, vector<int>& B)
{vector<int> C;int tmp = 0;for (int i = 0; i < A.size() || i < B.size() || tmp; i++){if (i < A.size()) tmp += A[i];if (i < B.size()) tmp += B[i];C.push_back(tmp % 10);tmp /= 10;}while (C.size() > 1 && C.back() == 0) C.pop_back();return C;
}int main()
{string a, b;cin >> a >> b;vector<int> A, B;for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');for (int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');auto C = add(A, B);for (int i = C.size() - 1; i >= 0; i--) cout << C[i];cout << endl;return 0;
}
代码测试:
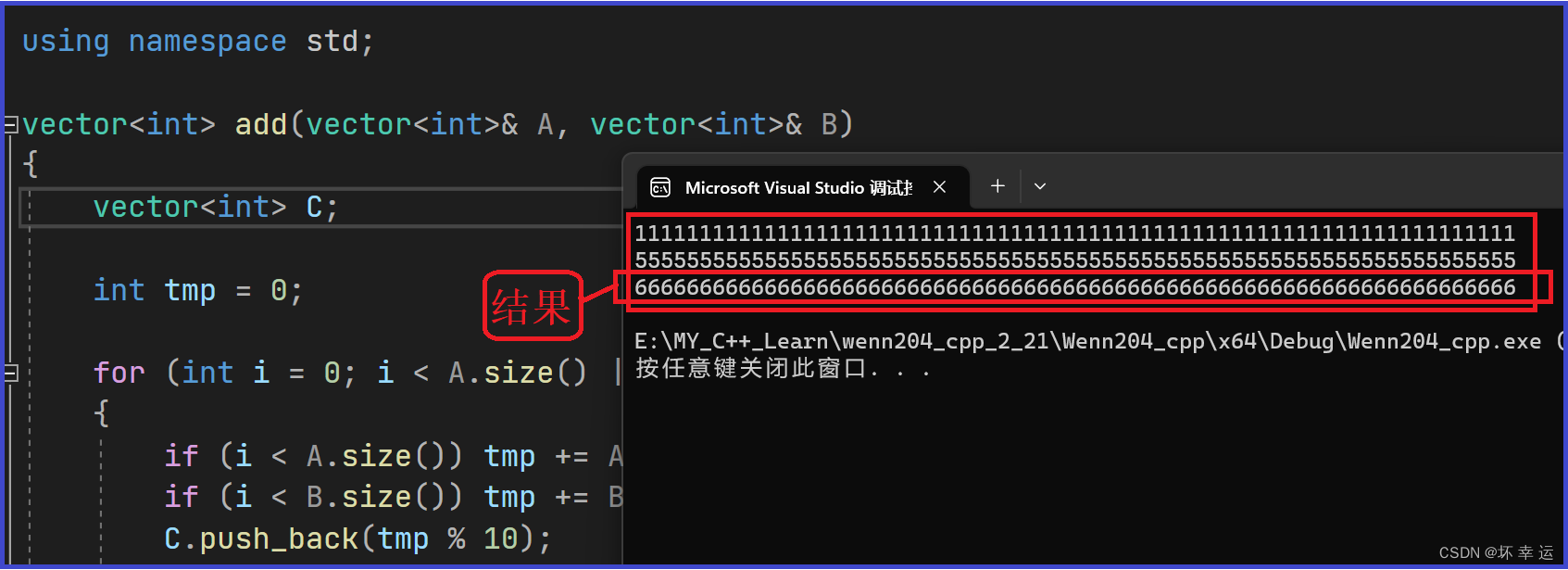
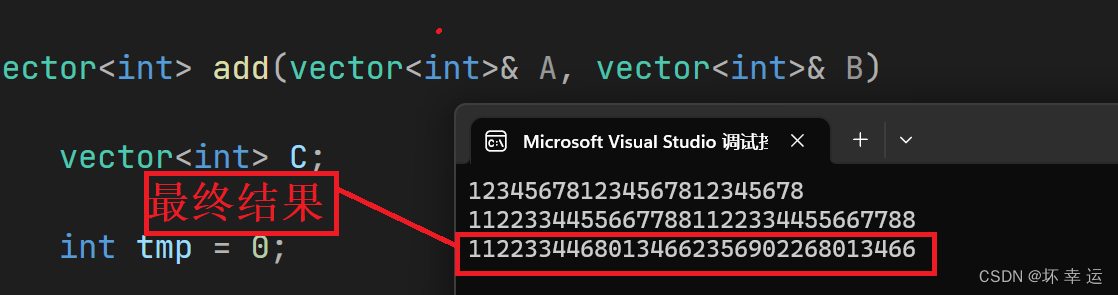
代码细节解释:
- 这里是将高精度数分别从低位到高位存放到两个
vector<int>中;
for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');for (int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
- 这个
for循环便是相加的代码,两个if表示如果这个数的位数加完了,就停止加入tmp,判断条件表示将tmp加完为止(也就是如果两个数位数相同,最高位相加完后又进了一位,此时 tmp 为 1 并且不在加入数据,这个1 也是有效位,因此需要加入C中)
for (int i = 0; i < A.size() || i < B.size() || tmp; i++){if (i < A.size()) tmp += A[i];if (i < B.size()) tmp += B[i];C.push_back(tmp % 10);tmp /= 10;}
- 这个
while表示去掉前导0,虽然加法不会出现前导0的情况,但不排除输入的数据都为0的情况。
while (C.size() > 1 && C.back() == 0) C.pop_back();
2.高精度减法
-
高精度减法是两个很高位数的数相减,值得注意的是,减法需要借位,并且相减会出现结果为正还是负的情况,因此,高精度减法的程序比高精度加法的程序稍复杂。
-
对于结果是正还是负的情况,我们可以写一个
cmp函数对存放两个高精度数的string进行比较,然后规定sub函数第一个参数为大的那个数,我们只要将大的那个传入第一个参数即可。如果是第二个输入的高精度数较大,在打印结果的时候先打印一个‘ - ’即可。 -
在进行相减的时候,我们可以先定义一个标记借位的变量
tmp(初始化为0),如果一位上相减为负数,说明需要向前借一位,所以在减的循环中第一条语句可以为:tmp = big[i] - tmp;,如果结果小于零,将tmp置为1,等进入下一次循环,第一条语句就自动减一,起到借位的效果。 -
那么结果小于
0,我们该如何确定这一位的最终答案呢?我们只需要在push_back时,里面的参数设为(tmp + 10)% 10,这样就可以处理tmp所有的情况了(详细点看代码注释)。 -
由于我们是通过将高精度数的每一位存入数组来计算的,并且减法会出现最高位依次连续是
0的情况,因此作为答案的数组,高位可能存放有0,在打印的时候这些0都会被打印出来,所以这里要有删去高位0的操作。
下面是相关操作的代码实现:
#include <iostream>
#include <vector>
using namespace std;bool cmp(vector<int>& A, vector<int>& B)
{if (A.size() != B.size()) return A.size() > B.size();// 这一步说明A,B两个高精度数长度相等,此时从最高位依次比较for (int i = A.size() - 1; i >= 0; i--)if (A[i] != B[i])return A[i] > B[i];return true;
}vector<int> sub(vector<int>& A, vector<int>& B)
{vector<int> C;int tmp = 0; // 用来标记借位// 这里A要大,所以 i < A.size()for (int i = 0; i < A.size(); i++){tmp = A[i] - tmp; // 表示上一步有没有借位if (i < B.size()) tmp -= B[i];// (tmp + 10) % 10 这是因为:// 当tmp<0时,说明这一位A的小于B的,因此要借位// 所以tmp+10后就相当于借位后的数,%10后便是留在这一位的最终结果// 当tmp>0时,说明这一位A的大于B的,尽管加了10// 但%10后加10与不加10是一样的(可脑补一下)C.push_back((tmp + 10) % 10);// 如果tmp<0,表示这一位A的小于B的,因此将tmp置为1,下一次循环的第一步减去一if (tmp < 0) tmp = 1;else tmp = 0;}// 由于高位会出现0的情况(22226 - 22223 = 3),所以这里要去前导0while (C.size() > 1 && C.back() == 0) C.pop_back();return C;
}int main()
{string a, b;cin >> a >> b;vector<int> A, B;for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');for (int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');if (cmp(A, B)){auto C = sub(A, B);for (int i = C.size() - 1; i >= 0; i--) cout << C[i];}else{auto C = sub(B, A);cout << '-';for (int i = C.size() - 1; i >= 0; i--) cout << C[i];}return 0;
}
代码测试:
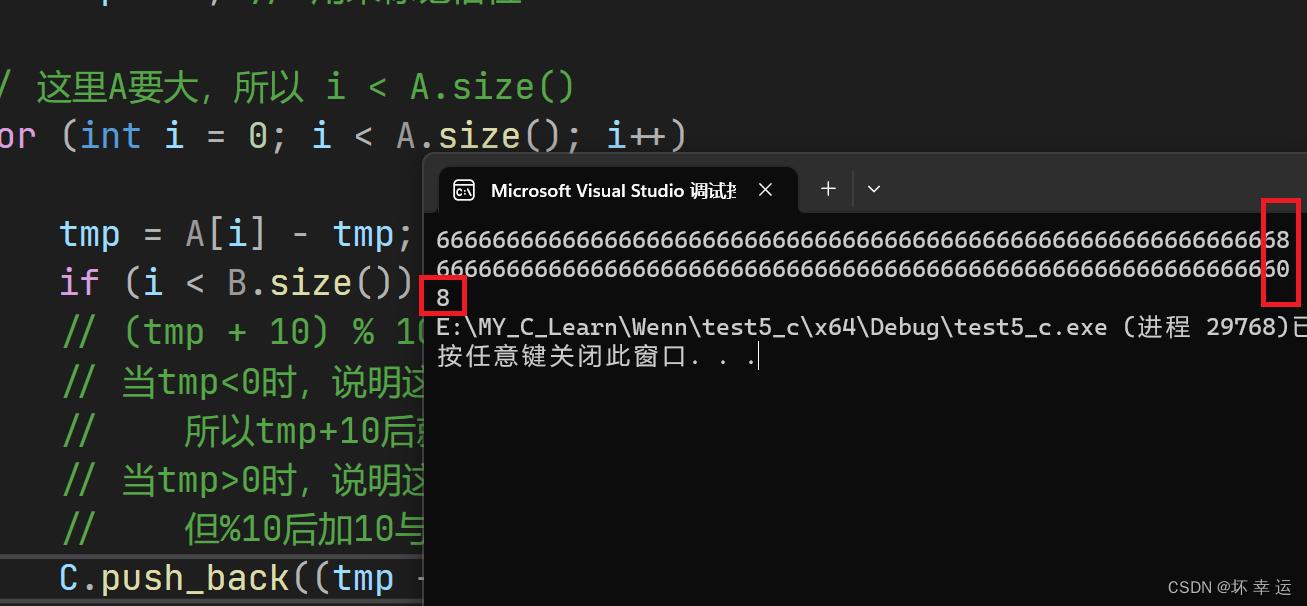
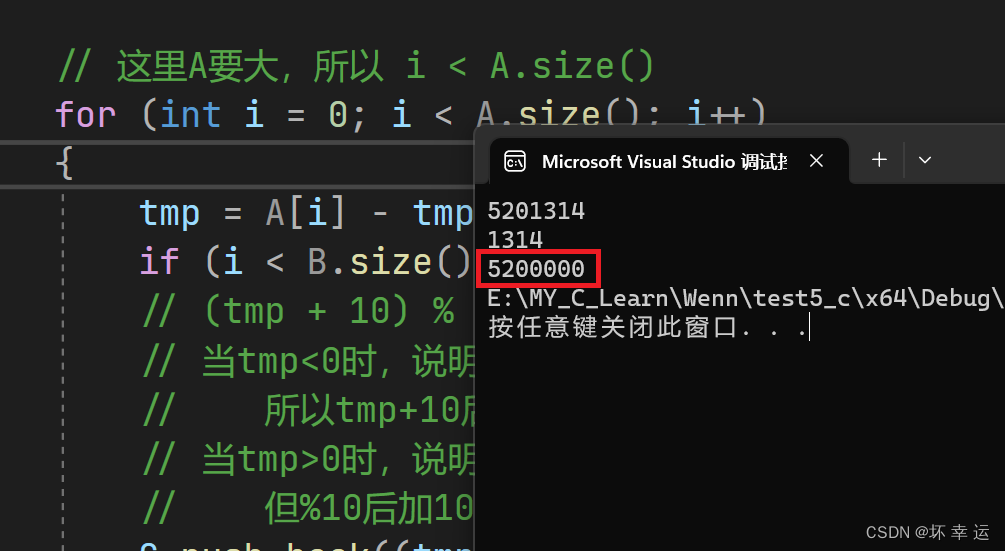
3.高精度乘法
-
在学完高精度加法和减法后,对于高精度乘法理解起来是很快的,这里我们规定,输入的第一个数为高精度数,第二个数为
int范围内的数,并且两个数都是正整数。 -
有了上面的规定,接下来的操作就简单了,我们只需要关注如何乘,如何
push,以及去前导0即可。 -
相乘前的准备与高精度加减类似,只不过输入的其中一个参数变为了
int。 -
整个相乘的过程:定义一个
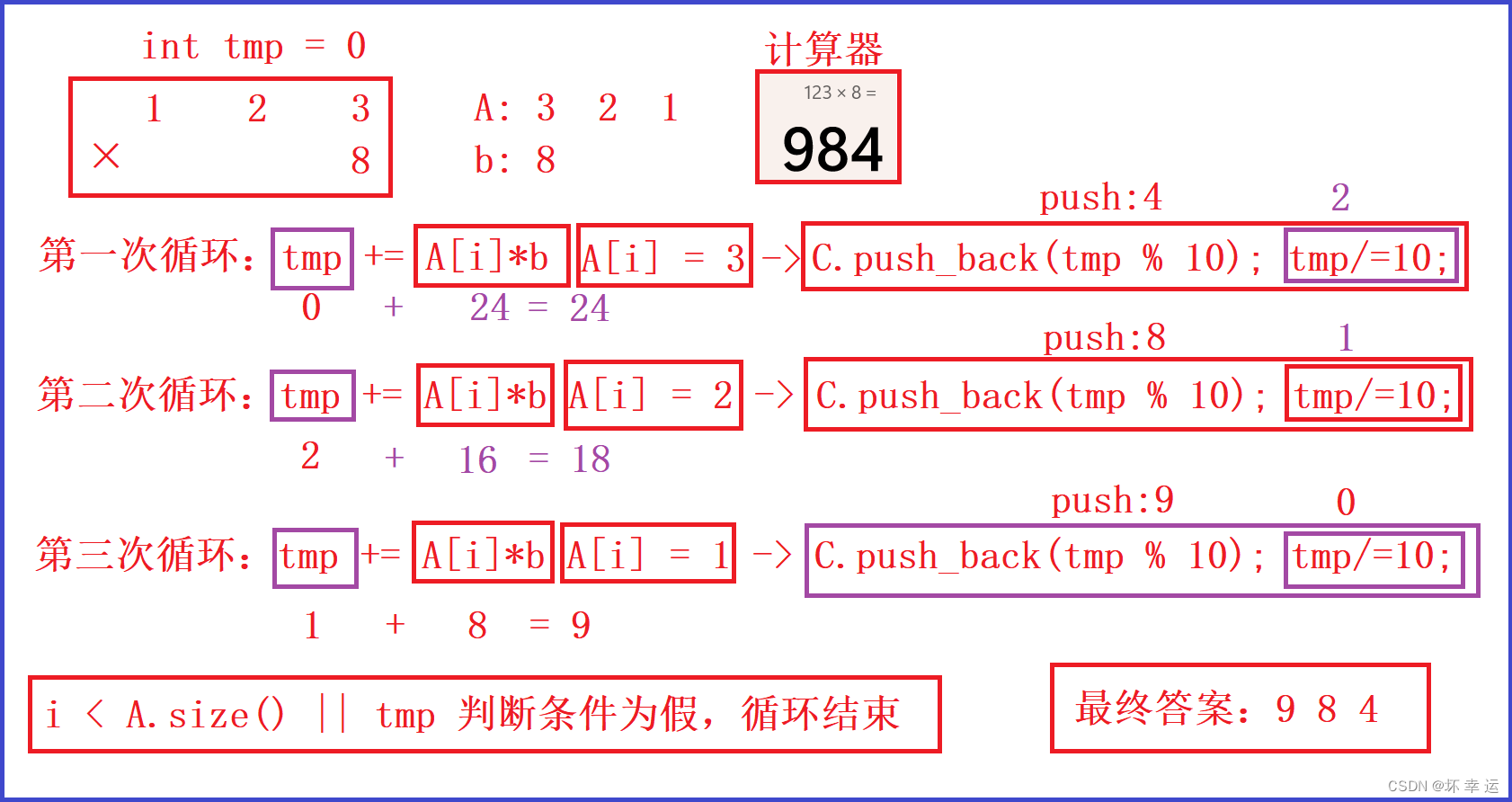
tmp,将高精度数的每一位与int数相乘加入tmp(每一次循环将每一位相乘后的结果加入tmp),然后每一次循环中,将tmp%10(每次取出个位上的数)push_back,再tmp/=10丢掉个位上的数,直到高精度的每一位数都乘过或者tmp为0循环结束,这样就完成了高精度的乘法。 -
如果输入的两个数有
0,那么结果终究会是0,所以高精度乘法也要有去除前导零的操作。
下面是相关操作的代码实现:
#include <iostream>
#include <vector>using namespace std;vector<int> mul(vector<int>& A, int b)
{vector<int> C;int tmp = 0;for (int i = 0; i < A.size() || tmp; i++){// 如果A没有遍历完就一直将每一位与b相乘加入tmpif (i < A.size()) tmp += A[i] * b;// (tmp % 10)是push tmp的个位C.push_back(tmp % 10);// 丢弃个位tmp /= 10;}while (C.size() > 1 && C.back() == 0) C.pop_back();return C;
}int main()
{string a;int b, flag = 1;cin >> a >> b;vector<int> A;for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');auto C = mul(A, b);for (int i = C.size() - 1; i >= 0; i--) cout << C[i];return 0;
}
代码测试:
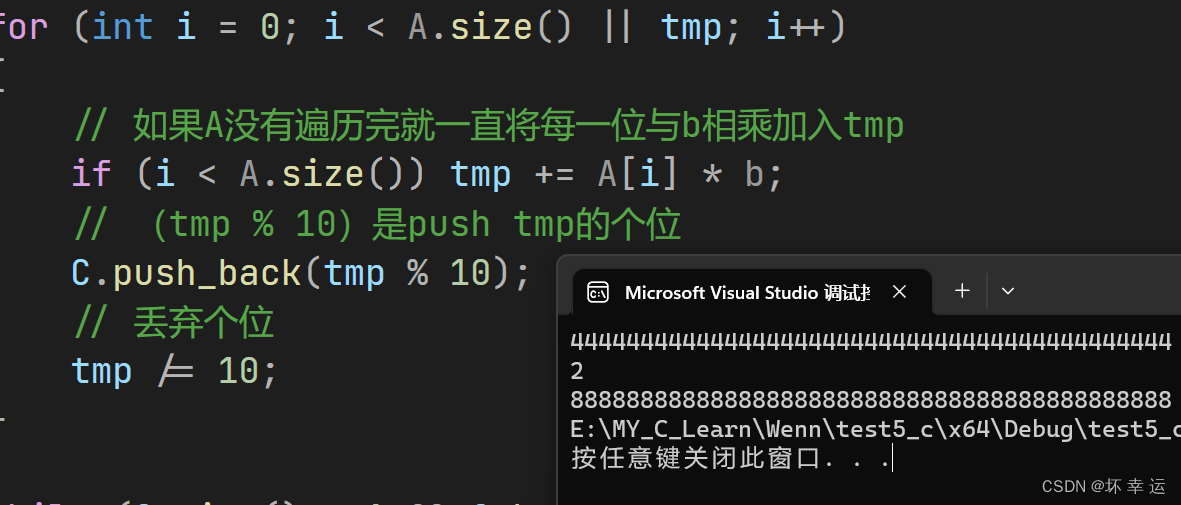
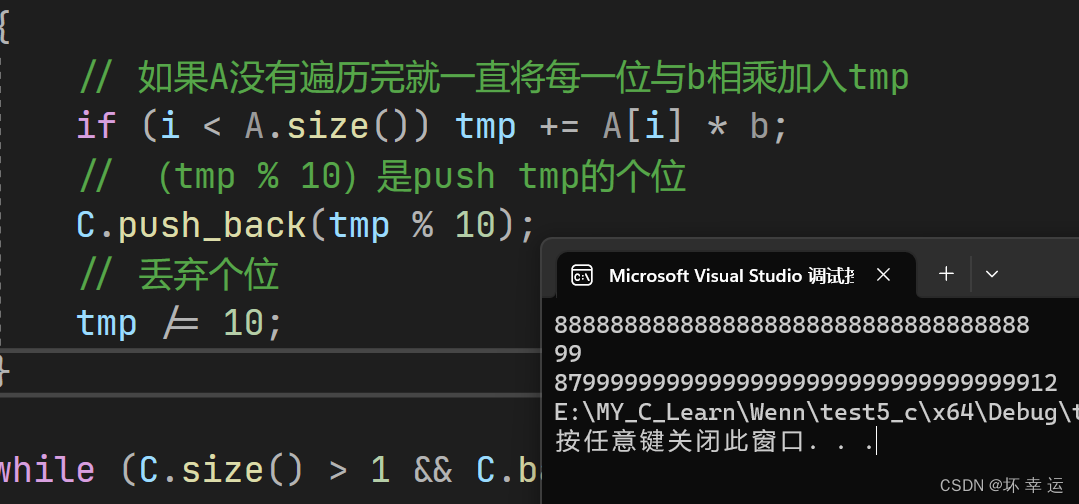
选取测试案例图解:
4.高精度除法
-
高精度除法与高精度乘法相比,多了一个变量
r用来储存余数,其余的输入与乘法相同,但最后输出要把r打印。同样的,这里我们规定,两个数都是正整数,并且int范围内的那个数不能为0(一个高精度数除以一个int范围内的整数)。 -
对于整个相除的过程,肯定也是需要一个循环的。我们都知道,每一位相处的余数,都要相当于乘以
10与下一位相加,由于r初始为0,因此循环的第一句可以写为r = r * 10 + A[i],A[i]为当前位的数,r*10表示上一位数相除得到的余数,如果上一位数余数为零,则这个表达式结果为0。 -
执行完上一条语句后便得到了被除数,此时就可以
push:r / 除数,表示当前位的结果,最后再r %= 除数除去除完的除数,这样整个过程就设计完成了。 -
由于
main函数打印正确答案是从尾开始将每一位打印到头的,并且正确答案是由高位到低位从数组的头依次存放的,因此下一步需要逆置一下结果数组。 -
最后,除法会有高位为
0的情况,因此还要有一步去除前导0的操作。
下面是相关操作的代码实现:
#include <iostream>
#include <vector>
#include <algorithm>using namespace std;// 要改变main函数里的余数r,因此要引用
vector<int> div(vector<int>& A, int b, int& r)
{vector<int> C;// 根据除法的过程,从高位开始除for (int i = A.size() - 1; i >= 0; i--){// r开始为0,则第一次循环就为A的最高位与b相除// 如果 r>b 则会有余数 ,所以下一次循环将这个余数 乘以10+A[i] 便是第二次循环要除的数// 如果 r<b 则余数就是r本身,第三条语句 r%=b 就相当于没执行过r = r * 10 + A[i];C.push_back(r / b); // push 这一次除b的结果,如果r<b,则push:0r %= b;}// 由于得到的结果是从高位向低位开始存的,所以这里逆置一下,便于去除前导0reverse(C.begin(), C.end());// 除法会出现0的情况,因此这里要处理前导0while (C.size() > 1 && C.back() == 0) C.pop_back();return C;
}int main()
{string a;// b为int范围内的数// 创建一个变量r来储存余数int b, r = 0;cin >> a >> b;// A用来储存高精度数vector<int> A;for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');auto C = div(A, b, r);// 打印还是与前面一样,因为div中结果逆置了for (int i = C.size() - 1; i >= 0; i--) cout << C[i];// 这里打印余数cout << endl << r << endl;return 0;
}
代码测试:
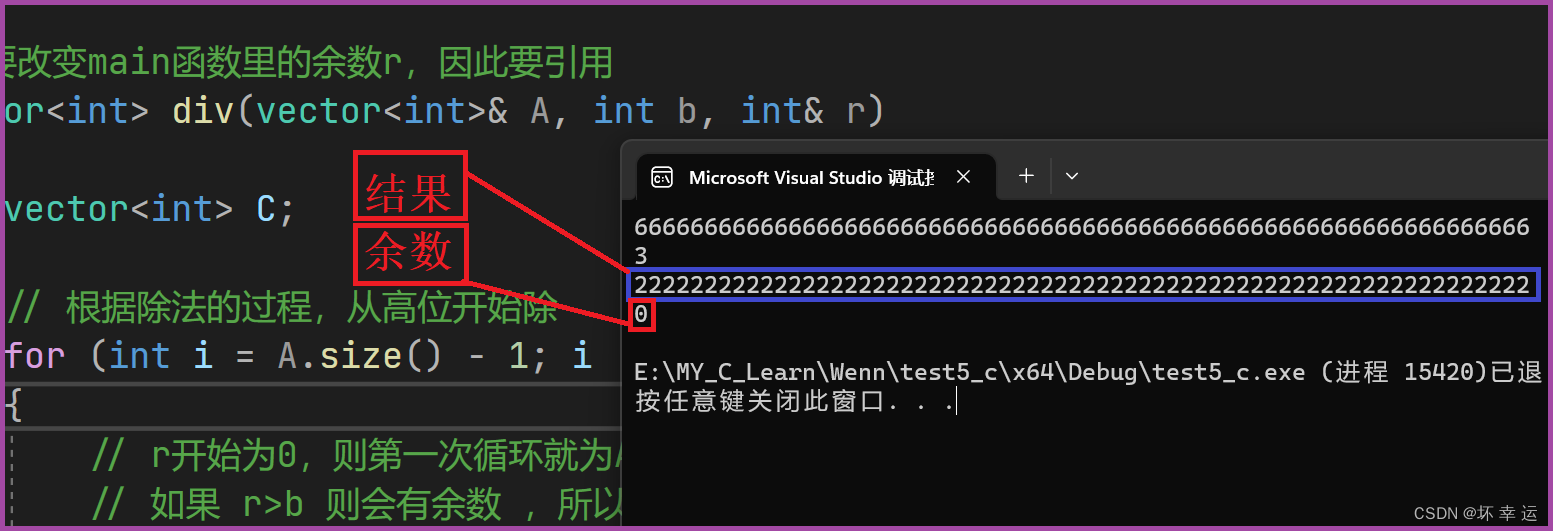
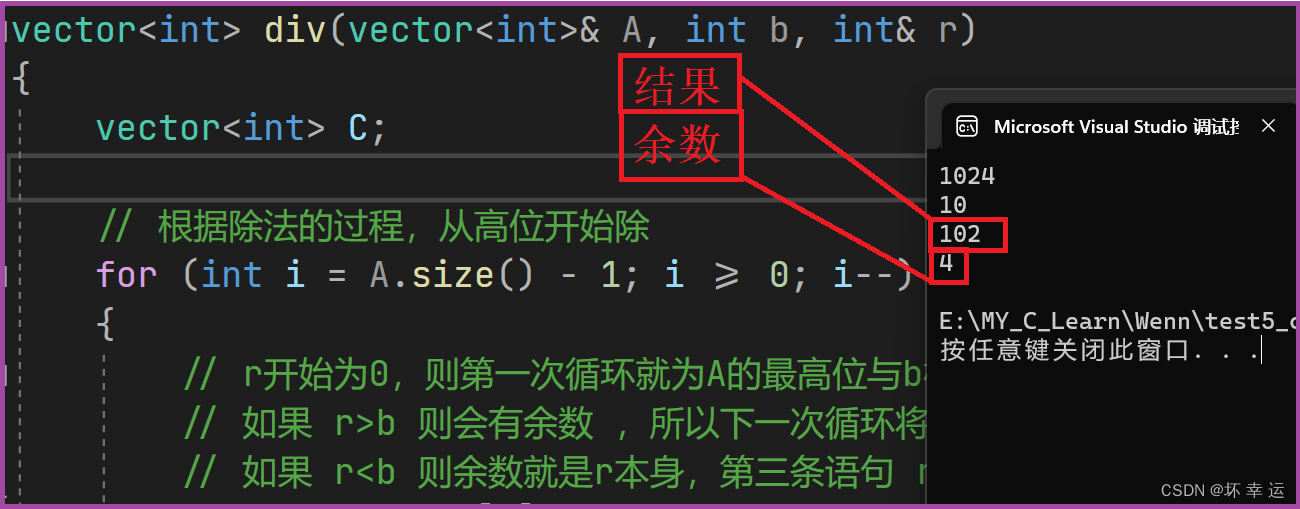
选取测试案例图解:
输入
128
8
输出
16
0

写在最后
上述可以说都是高精度计算的基础模板,实际上在很多题目中都可以用到这一模板,比如某些链表的题。所以我们要增强对这一类模板的熟练度,以便在后面的刷题中遇到能用此模板解决的问题能够想起来有这一模板可以用。
感谢阅读本小白的博客,错误的地方请严厉指出噢!
相关文章:

【基础算法】关于高精度计算的问题【很高位数数据的加减乘除(相关代码用C++实现)】
文章目录前言1.高精度加法2.高精度减法3.高精度乘法4.高精度除法写在最后前言 当我们在利用计算机进行一些计算时,可能会遇到这类问题 : 有些计算要求精度高,希望计算的数的位数可达几十位甚至几百位,虽然计算机的计算精度也算较…...
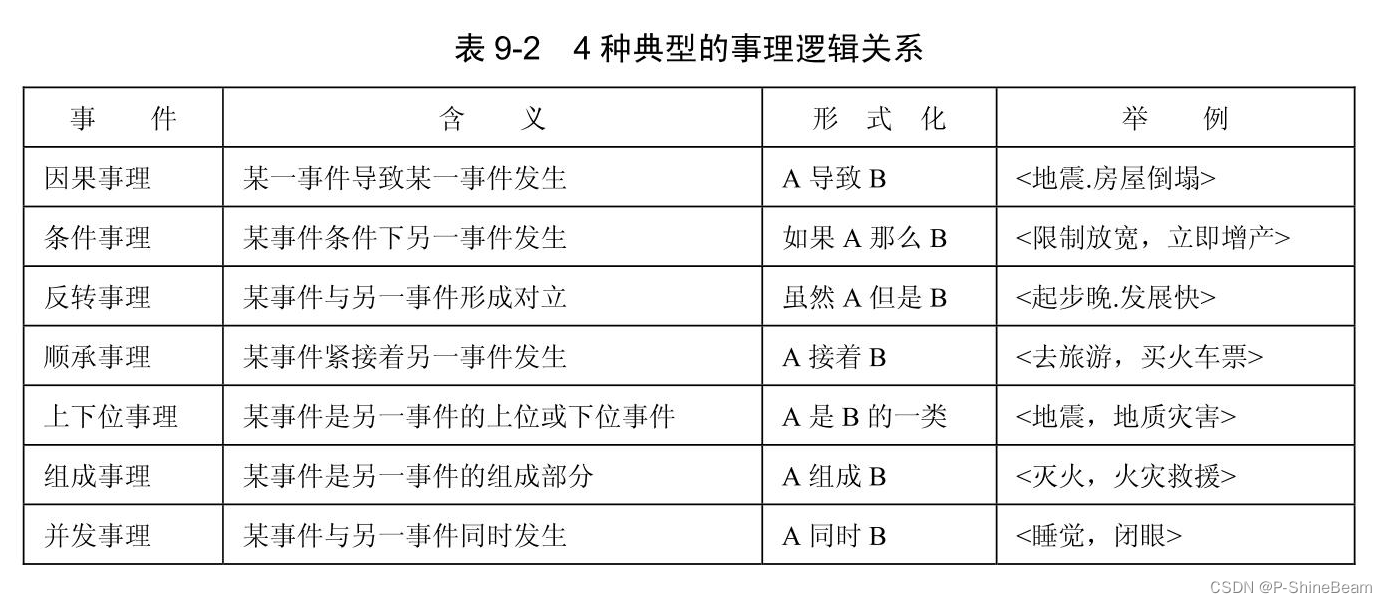
事理知识图谱
事理知识图谱能够有力第建模各类事件之间的演化关联关系为事理逻辑推理提供更好的数据基础。 事理图谱定义 事理知识图谱可以将文本中对事件以及事件之间的关系抽取并抽象出来,构建成一个有向图形式的事理知识库。在结构上,事理知识图谱是一个有向有环…...

多綫程之python爬蟲構建
目录多綫程定義簡介原理优点缺点优势代碼框架實現導包打印類爬蟲類構造方法獲取代理設置headers獲取新session獲取源代碼解析網頁解析子頁面保存數據綫程任務得到url啓動多綫程爬蟲總結多綫程 以下定義來自百度百科,看看就好沒仔細寫 定義 多线程(mul…...

【干货】Redis在Java开发中的基本使用和巧妙用法
Redis是一款高性能的内存数据结构存储系统,能够支持多种数据结构类型,如字符串、哈希、列表、集合、有序集合等,也能够支持高级功能,如事务、发布/订阅、Lua脚本等,具有高可用性、高并发性和可扩展性的优点。在Java开发…...

历时半年,我终于阿里上岸了,附面经和Java非科班学习心得
个人经历 本科双非化学,跨考了电子硕士,研究生依然双非。无互联网实习,无比赛无论文。(研究生研究方向是车辆电子和楼宇自动化,有自动化和高校实训讲师相关的实习经历) 21年11开始学Java准备秋招。 阿里上…...

ArkUI实战,自定义饼状图组件PieChart
本节笔者带领读者实现一个饼状图 PieChart 组件,该组件是根据笔者之前封装的 MiniCanvas 实现的, PieChart 的最终演示效果如下图所示: 饼状图实现的拆分 根据上图的样式效果,实现一个饼状图,实质就是绘制一个个的实…...
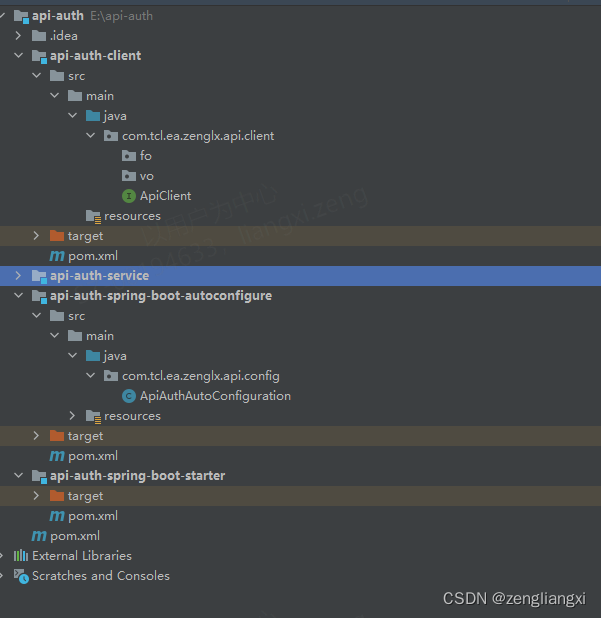
工作实战之系统交互api调用认证设计
目录 前言 一、黄金段位接口交互 二、钻石段位接口交互设计 1.接口文档定义 2.工具类以及demo提供 a.调用方部分代码 b.被调用方 三.星耀段位接口访问设计 1.在钻石段位的基础上,进行sdk的封装 a.maven引入 b.sdk包含工具类 四.王者段位接口访问设计 1.开发详情 2.…...

学习系统编程No.5【虚拟地址空间】
引言: 北京时间:2023/2/22,离补考期末考试还有5天,不慌,刚午觉睡醒,闹钟2点20,拖到2点50,是近以来,唯一一次有一种睡不醒的感觉,但是现在却没有精神,因为听了…...
)
Linux常用指令(未完待续。。。)
* basename:只留下路径的“最后一部分” X、文件夹&目录操作 复制 :cp /xxx /xxx - a 该选项通常在拷贝目录时使用。它保留链接、文件属性,并递归地拷贝目录,其作用等于dpR选项的组合; - d 拷贝时保留链接&#…...

用D写裸机
原文 用D编写裸机RISC-V应用 这篇文章展示,如何用D编写,目标为RISC-VQEMU模拟器的程序裸机"你好".项目 为什么是D? 我最近一直在用C编写裸机代码,我有点对C缺乏特征感到沮丧.D引入了叫betterC的模式(基本上禁止了D运行时的所有语言功能).使得D裸机编程大致与C一…...

(二十五)、实现评论功能(5)【uniapp+uinicloud多用户社区博客实战项目(完整开发文档-从零到完整项目)】
1,实现二级回复的入库操作 1.1 两个子组件(comment-item和comment-frame)与父组件reply之间的属性传值 comment-item: props: {item: {type: Object,default () {return {}}}},comment-frame: props: {commentObj: {…...
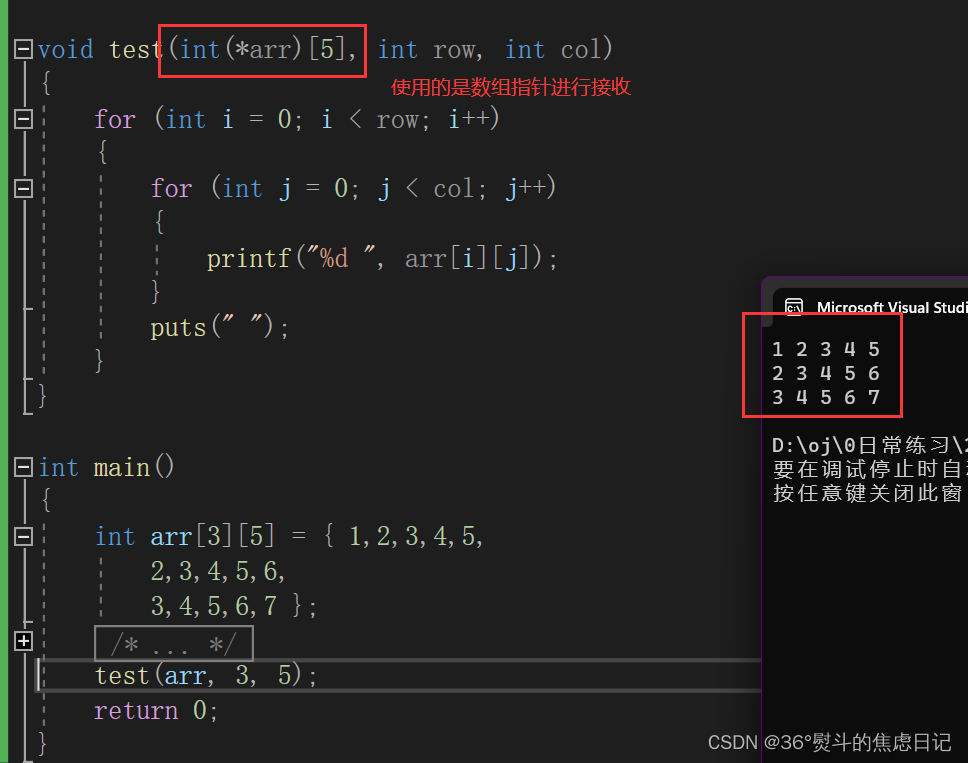
【概念辨析】二维数组传参的几种可能性
一、二维数组传参竟然不是用二级指针进行接收? 今天进行再一次的二级指针学习时,发现了一条以前没怎么注意过的知识点:二维数组进行传参只能用二维数组(不能省略列)进行接收或者是数组指针。 问题复现代码如下…...
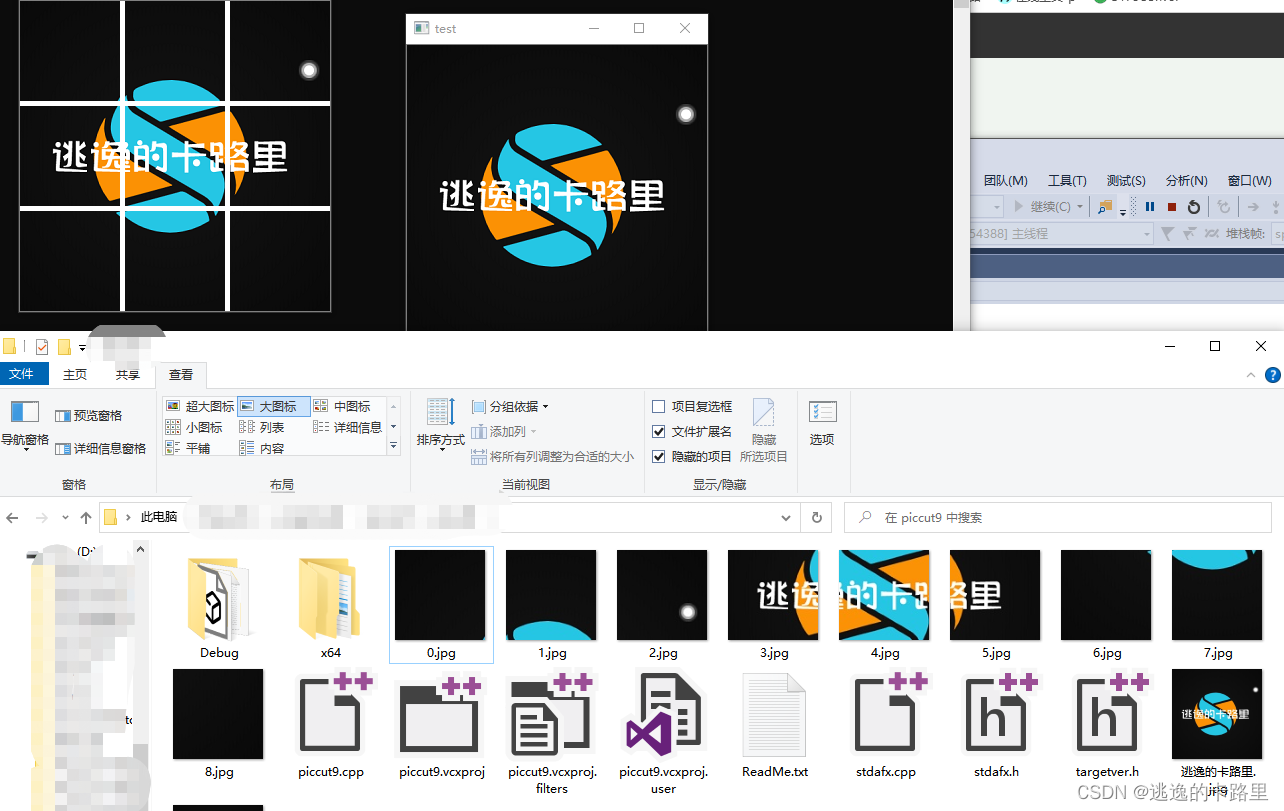
python和C++代码实现图片九宫格切图程序(附VS2015配置Opencv教程)
1、python代码实现图片分割成九宫格 需要包含的库,没有下载安装的,需要自己安装哦。 实现原理很简单,就是用PIL库不断画小区域,切下来存储成新的小图片。 假设每一个格子的宽和高分别是w、h,那么第row行(…...
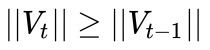
【深度学习】优化器
1.什么是优化器 优化器是在深度学习的反向传播过程中,指引损失函数(目标函数)的各个参数往正确的方向更新合适的大小,使得更新后的各个参数让目标函数不断逼近全局最小点。 2.优化器 2-1 BGD 批量梯度下降法,是梯度下…...
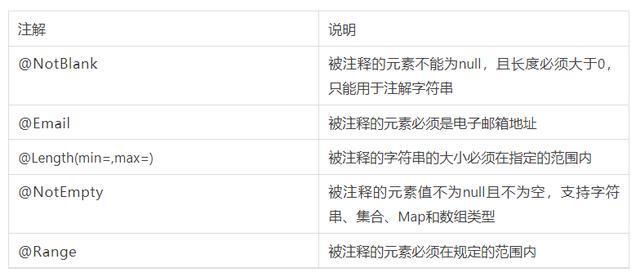
SpringBoot使用validator进行参数校验
Validated、Valid和BindingResultBean Validation是Java定义的一套基于注解的数据校验规范,比如Null、NotNull、Pattern等,它们位于 javax.validation.constraints这个包下。hibernate validator是对这个规范的实现,并增加了一些其他校验注解…...
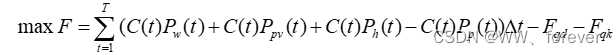
论文复现:风电、光伏与抽水蓄能电站互补调度运行(MATLAB-Yalmip全代码)
论文复现:风电、光伏与抽水蓄能电站互补调度运行(MATLAB-Yalmip全代码) 针对风电、光伏与抽水蓄能站互补运行的问题,已有大量通过启发式算法寻优的案例,但工程上更注重实用性和普适性。Yalmip工具箱则是一种基于MATLAB平台的优化软件工具箱,被广泛应用于工程界优化问题和…...
FastCGI sent in stderr: "PHP message: PHP Fatal error
服务器php7.2卸载安装7.4之后,打开网站一直无法访问,查看nginx错误日志发现一直报这个错误:2023/02/23 11:12:55 [error] 4735#0: *21 FastCGI sent in stderr: "PHP message: PHP Fatal error: Uncaught ReflectionException: Class translator does not exist in …...
)
【数字IC基础】跨时钟域(CDC,Clock Domain Crossing)
文章目录 一、什么是跨时钟域?二、跨时钟域传输的问题?2、1 亚稳态(单bit:两级D触发器(双DFF))2、2 数据收敛(多bit亚稳态)(格雷码编码、握手协议、异步FIFO、DMUX)2、3 多路扇出:(先同步后扇出)2、4 数据丢失(延长输入数据信号):类似脉冲展宽2、5 异步复位(…...

UNI-APP学习
uni-app的基本使用 uni-app介绍 官方网页 uni-app 是一个使用 Vue.js 开发所有前端应用的框架,开发者编写一套代码,可发布到iOS、Android、H5、以及各种小程序(微信/支付宝/百度/头条/QQ/钉钉)等多个平台。 即使不跨端…...

编译原理【运行时环境】—什么是活动记录、 活动记录与汇编代码的关系
系列文章戳这里👇 什么是上下文无关文法、最左推导和最右推导如何判断二义文法及消除文法二义性何时需要消除左递归什么是句柄、什么是自上而下、自下而上分析什么是LL(1)、LR(0)、LR(1)文法、LR分析表LR(0)、SLR(1)、LR(1)、LALR(1)文法之间的关系编译原理第三章习…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
