C++ - 双指针_盛水最多的容器
盛水最多的容器
11. 盛最多水的容器 - 力扣(LeetCode)
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
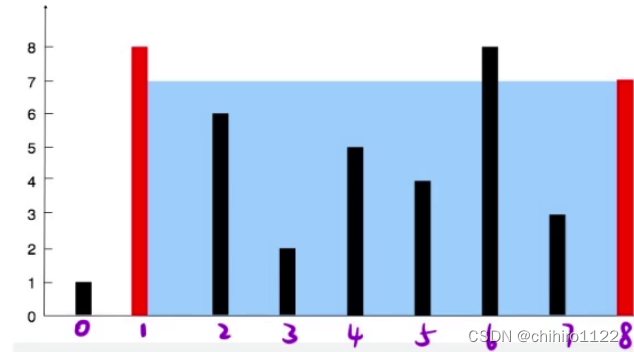
输入:[1,8,6,2,5,4,8,3,7]
输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。
在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。数组的长度是 高height,每一个数组都是一个边(墙壁),要求找两个数组(边),使得盛水最多,也就是要找出两个height最大的数组。
根据木桶效应,当我们往这个最大的容器当中注水,这个水的高度 height就是第二大的数组的长度。所以上述盛水最多的容器的体积就是 7 x 7 = 49。
即使 6 号数组的高度也是最高,我们选择 1 和 6 的话,计算出来的体积是 5 x 8 = 40 ,是小于 49 的,所以也不能选。
暴力解法
这道题的暴力解法还是非常简单的,无非就是找出 两个最长的数组,但是不是单单选出两个最长的数组,还要看两个数组之间距离,我们要的是 两个数组之间的距离 和 两个数组的小的那个的长度的乘积为最大。
利用两层 循环句可以搞定,外层固定一个数组,内层一次往后找数组,当有更大的出现,就记录这个更大体积和两数组的位置。
但是,这种解法不好,时间复杂度高。而且实现简单,这里就不实现了。
双指针
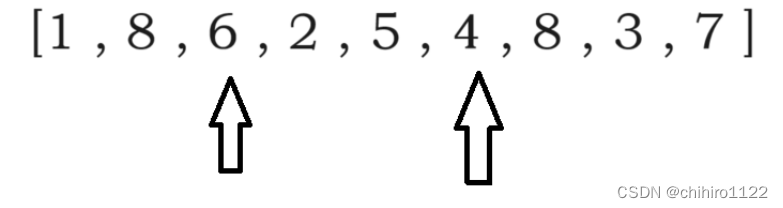
我们先随便取出一个区间来分析。
比如 6 2 5 4 这个区间,我们取 6 和 4 两个数组,此时一定可以计算出一个具体的体积:
h * w = v
那么此时,如果我们把 4 作为固定边,另一边向内枚举,那么 w 宽度一定是减少的。在此基础之上,我们来看高度的变化。
高度的变化有两种(如下图所示):
- 一种是 4 像内枚举的过程当中,找到一个 比 4 小的数,那么此时 的 h 高度就减少,那么 h 和 w 都减少,那就计算出来的体积一定是减少的。
- 第二种是 找到 一个 和 4 高度相等或者 比4 大的 数组,相等就不看了,大的话计算的高度是取 小的那个,也就是 4 的高度,那么此时,h 不变,但是 w 依旧减少,计算出的体积也一定是减少的。
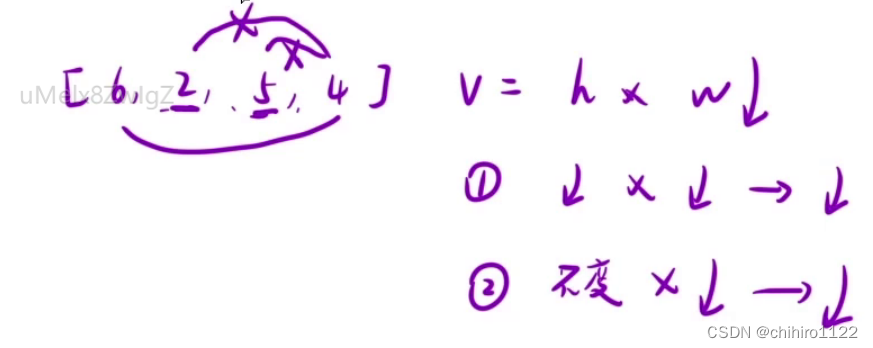
那么,以 4 为固定边,向 6 ---- 4 区间之内 枚举 4 和 某一个数组的组合的话,计算出来的体积一定是 减少的,那么其中的例子也就不需要进行枚举了。我们可以大胆的把 这个 结点 干掉。
按照上述过程,我们就可以把区间放大,开始就是整个区间:

当计算出体积之后,就干掉小的那一个,然后往中间枚举就行了:
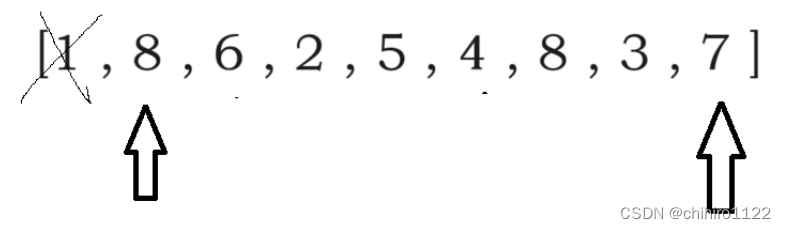
那么,当我们计算到 两个指针相遇的时候,一定算出了很多个 体积的值了,那么我们只需要选出最大的体积就行了。
代码实现:
class Solution {
public:int maxArea(vector<int>& height) {int left = 0, right = height.size() - 1, ret = 0;while(left < right){// 计算体积int v = (min(height[left], height[right])) * (right - left);ret = max(ret, v);if(height[left] < height[right]){left++;}else{right--;}}return ret;}
};快乐数
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
- 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
- 如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
示例 1:输入:n = 19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1我们用 19 来分析:
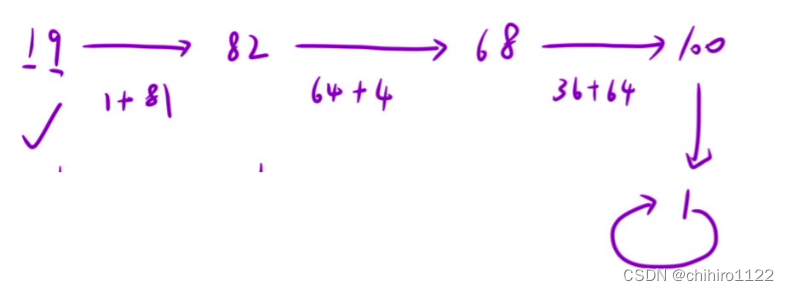
19 是 快乐数,我们发现,计算到最后都会是 1 的旋转;
再用不是 快乐数的 数来分析:
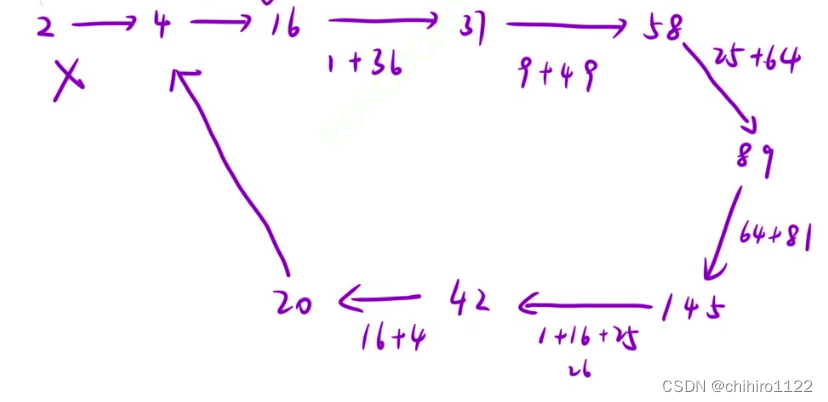
我们发现,如果不是快乐数的话,它也会在其中,以其中的某一个数作为结点构成一个循环。
那么上述的这两种结构,就类似于是 循环链表这个题目,我们在 循环链表题目当中,判断一个链表是否带环,是用快慢指针来判断的,用一个 一次走一个结点的 slow 指针,和一个 一次走 两个结点的 fast 指针来判断。
如果链表当中带环的话,那么 两个指针往后遍历,肯定会走到 环当中,那么在一个无限循环的环当中,一个指针快,一个指针满,两个指针一定会相遇。所以我们使用 指针是否会相遇来判断一个链表是否带环。
那么上述的例子也是一样的,两种情况一定带环,说明两个指针一定会相遇。
如果是快乐数的话,循环当中的数都是1;如果不是的话,循环当中的数就不是1;
代码实现:
class Solution {
public:int sum(int x){int sum = 0;while(x){int mold = x % 10;sum += mold * mold;x /= 10;}return sum;}bool isHappy(int n) {int left = n, right = sum(n);while(left != right){left = sum(left);right = sum(sum(right));}return left == 1;}
};三数之和
15. 三数之和 - 力扣(LeetCode)
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。这里的 “答案中不可以包含重复的三元组”,意思就是 上述 的 [-1,0,1] 和 [0 , 1 ,-1] 这两组。虽然是利用不同的元素组合出来的,但是这两者重复的三元组。所以只能取一个。
暴力解法
暴力解法就是 暴力枚举,把每一种组合方式都列出出来,然后判断满足 三数之和的情况,然后在对满足的情况进行去重。
暴力枚举就不解释了,主要解释一下,去重的部分:
方式一:就是把每一个找出来的 三元组 都排个序,然后最后再来看有没有重复的三元组。
但是上述的方式比较的麻烦,因为一个数组当中可能会列出很多个 重复的三元组,那么我们在最后 来找这些相同的 三元组就会很麻烦,而且,对每一个三元组都排序,排序的效率可能就大于 我们使用排序的 时间复杂度了,因为有重复的三元组,相当于是对 大于 数组个数的元素进行排序。
所以,我们使用一种更好的方式,就是在找三元组之前,先把数组排好序,这样的话,在数组当中重复的元素就都在一起了。
我们发现,出现重复的三元组的原因在于,数组当中有重复的元素,那么我们就像把 重复 元素删除掉,这样在寻找三元组之后就不会再有重复的三元组了。
去重的话,C++ 当中有一个 set 容器,是利用 二叉搜索树 的底层来实现的,在插入元素的过程当中就会自动的进行去重。
当我们对数组进行排序之后,因为重复的元素都在一起了,所以此时我们在找出的重复三元组的结果是一样的:
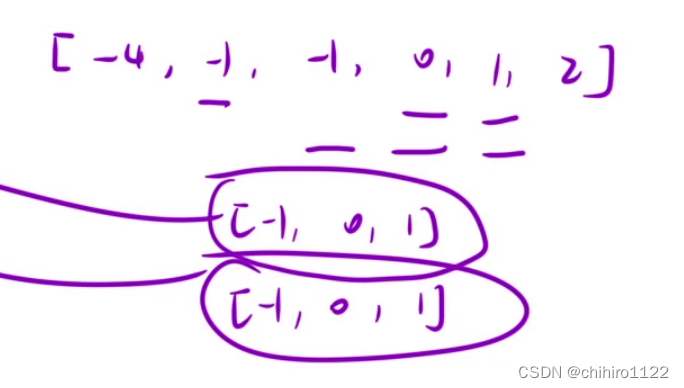
重复的三元组,都是按照有序的方式进行组合的。
那么,我们就把组合出来的 三元组放到 set 容器当中,这样 set 容器就可以帮我们进行自动去重三元组。
当然,因为是暴力解法,所以时间复杂度肯定不高,而且我们还要对数组进行排序等等操作。
双指针
同样,要先对数组进行排序,排序之后,先固定一个数 a,然后在这个数的后面区间当中去利用双指针 求出找到 两数之和 为 -a 的情况。
需要注意的是,后续利用双指针找两数的时候,要注意不能找漏,当我们找到一组 两数 符合 规则,不能停下来要继续找。
还有,去重:
在 双指针的区间当中,如果 left 或者 right 已经找到一种 符合结果的三元组的了,当 left 或者 right 需要往中间迭代的时候,如果其中一个指针找到 和 迭代之前相同的元素,就不用进行对这个数的寻找了,可以跳过:
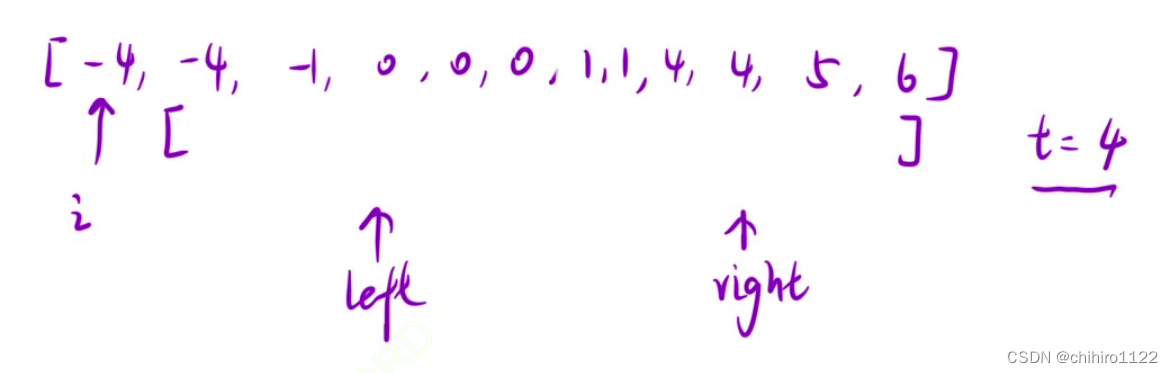
此时的 left 指向的是 0 ,0 已经和right 指向的元素的枚举过了,那么 此时 left 后面的 0 就没有必要在进行 枚举了,因为枚举出来的结果都一样,重复的。直接跳过就行。
而且,不止在双指针区间当中,在固定的数 i 也是一样的,当 i 的右边双指针区间 枚举完毕之后,i 是要往后迭代,但是如果 i 迭代之后,i 还是和原来的数 是一样的,那么枚举出的结果肯定也是一样的,所以就没有必要枚举了,直接跳过即可。
而且,因为数组的是有序的,所以当 i 指向的元素的值大于0 之后,右边就不可能有组合可以满足要求了。
left 一定是 小于 right的,这样可以防止越界。
双指针寻找的过程:
因为数组的是有序的,当在 区间当中找到的两数之和小于 -a ,说明 此时 left 的数太小, left++;如果 两数之和大于 -a,说明此时 right 的数太大,right--;
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> vv;sort(nums.begin(), nums.end());int i = 0;int n = nums.size();while(i < n){int left = i + 1, right = n - 1;int target = -nums[i];while(left < right){// 双指针判断if(nums[left] + nums[right] < target){left++;}else if(nums[left] + nums[right] > target){right--;}else{vv.push_back({nums[i], nums[left], nums[right]});left++;right--;// 去重 left 和 rightwhile(left < right && nums[left] == nums[left- 1]) left++; while(left < right && nums[right] == nums[right + 1]) right--;}}//去重ii++;while(i < n && nums[i] == nums[i - 1])i++;}return vv;}
};相关文章:

C++ - 双指针_盛水最多的容器
盛水最多的容器 11. 盛最多水的容器 - 力扣(LeetCode) 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的…...

分类预测 | Matlab实现NGO-CNN-SVM北方苍鹰算法优化卷积支持向量机分类预测
分类预测 | Matlab实现NGO-CNN-SVM北方苍鹰算法优化卷积支持向量机分类预测 目录 分类预测 | Matlab实现NGO-CNN-SVM北方苍鹰算法优化卷积支持向量机分类预测分类效果基本描述程序设计参考资料 分类效果 基本描述 1.Matlab实现NGO-CNN-SVM北方苍鹰算法优化卷积支持向量机分类预…...

分享一个java+springboot+vue校园电动车租赁系统(源码、调试、开题、lw)
💕💕作者:计算机源码社 💕💕个人简介:本人七年开发经验,擅长Java、Python、PHP、.NET、微信小程序、爬虫、大数据等,大家有这一块的问题可以一起交流! 💕&…...
高性能计算环境下的深度学习异构集群建设与优化实践
★深度学习;模式识别;图像处理;人工智能建模;人工智能;深度学习算法;强化学习;神经网络;卷积神经网络;人工神经网络;VIBE算法;控制系统仿真&#…...

Laravel框架 - Facade门面
1 、官方文档给出的定义 “Facades 为应用的 服务容器 提供了一个「静态」 接口。Laravel 自带了很多 Facades,可以访问绝大部分功能。Laravel Facades 实际是服务容器中底层类的 「静态代理」 ,相对于传统静态方法,在使用时能够提供更加灵活…...

算法通关村第16关【青铜】| 滑动窗口思想
1. 滑动窗口的基本思想 一句话概括就是两个快慢指针维护的一个会移动的区间 固定大小窗口:求哪个窗口元素最大、最小、平均值、和最大、和最小 可变大小窗口:求一个序列里最大、最小窗口是什么 2. 两个入门题 (1)子数组最大平…...

CentOS安装openjdk和elasticsearch
CentOS安装openjdk 文章目录 CentOS安装openjdk一、yum1.1search1.2安装openjdk 二、elasticsearch的启动和关闭2.1启动2.2关闭2.3添加服务 一、yum 1.1search yum search java | grep jdk1.2安装openjdk [roottest ~]# yum install java-1.8.0-openjdk -y 查看openjdk版本 …...

【新版】系统架构设计师 - 案例分析 - 信息安全
个人总结,仅供参考,欢迎加好友一起讨论 文章目录 架构 - 案例分析 - 信息安全安全架构安全模型分类BLP模型Biba模型Chinese Wall模型 信息安全整体架构设计WPDRRC模型各模型安全防范功能 网络安全体系架构设计开放系统互联安全体系结构安全服务与安全机制…...
)
数据库设计(火车订票系统)
为一个火车订票系统设计一个数据库是一个好的方法来训练你的数据库技巧。 其中有一些需要考虑到的复杂度。 过一些需求,并且创建表格。 为这个虚构的火车订票系统提出了10个需求。 我们将把其中每个添加到entity relational diagram(实体关系图&…...

qemu+docker在服务器上搭建linux内核调试环境
基于docker和qemu的操作系统实验环境 参考以上文章实现。 其中 docker run -it --name linux_qemu qemu /bin/bash #从qemu镜像启动一个容器linux_qemu,进入shell 要改为 docker run -it --name linux_qemu 3292900173/qemu /bin/bash另外,在vscode运行过程中,ssh远…...

Stable Diffusion 参数介绍及用法
大模型 CheckPoint 介绍 作用:定调了作图风格,可以理解为指挥者 安装路径:models/Stable-diffusion 推荐: AnythingV5Ink_v32Ink.safetensors cuteyukimixAdorable_midchapter2.safetensors manmaruMix_v10.safetensors counterf…...

打印大对象日志导致GC问题的解决
内容: rpc调用外部服务时,需要将req和resp的信息打印出来,以便于排查问题。但是有的rpc服务的resp信息过于庞大,比如resp中有List<>信息,list很大很大时会导致log.info打印信息时,产生GC,…...

【Docker】学习笔记
1. docker基本操作 镜像搜索 // 直接搜索镜像资源 docker search mysql // 搜索过滤 docker search --filter "is-officialtrue" mysql // 官方发布镜像拉取镜像 docker pull mysql查看本地镜像 docker images删除本地镜像 docker rmi mysql // 强制删除镜像 d…...

网易云信4K 8K RTC助力远程医疗的技术实践
// 编者按:随着近年来国家关于缓解医疗资源分配不均的一系列政策出台,远程医疗作为平衡医疗资源分配的有力手段,目前正处于强劲发展阶段。网易云信运用超高清RTC视频技术助力医疗行业实现了远程高清视频病理分析和手术示教等能力。LiveVide…...
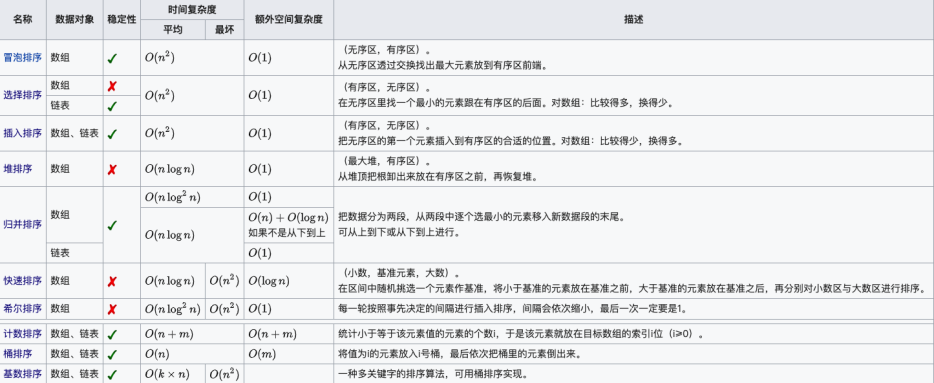
【排序算法】冒泡排序、插入排序、归并排序、希尔排序、选择排序、堆排序、快速排序
目录 几大排序汇总 1.冒泡排序 性能: 思路和代码: 2.插入排序 性能: 思路和代码: 3.归并排序 性能: 思路和代码: 4.希尔排序 性能: 思路和代码: 5.选择排序 性能: 思路和代码: 6.堆排序 性能: 思路和代码: topK问题 7.快速排序 性能: 思路和代码: 几大排…...

Linux学习笔记-应用层篇
1、Linux进程、线程概念/区别 Linux进程和线程是计算机系统中两种不同的资源分配和调度单位。 进程是计算机系统进行资源分配和调度的基本单位,也被认为是正在运行的程序。在面向线程的计算机结构中,进程是线程的容器。进程拥有独立的内存和系统资源&am…...

MySQL数据库的存储引擎
目录 一、存储引擎概念 二、存储引擎 2.1MyISAM 2.11MyISAM的特点 2.12MyISAM表支持3种不同的存储格式: 2.2 InnoDB 2.21InnoDB特点介绍 三、InnoDB与MyISAM 区别 四、怎么样选择存储引擎 五、查看存储引擎 六、查看表使用的存储引擎 七、修改存储引擎 …...
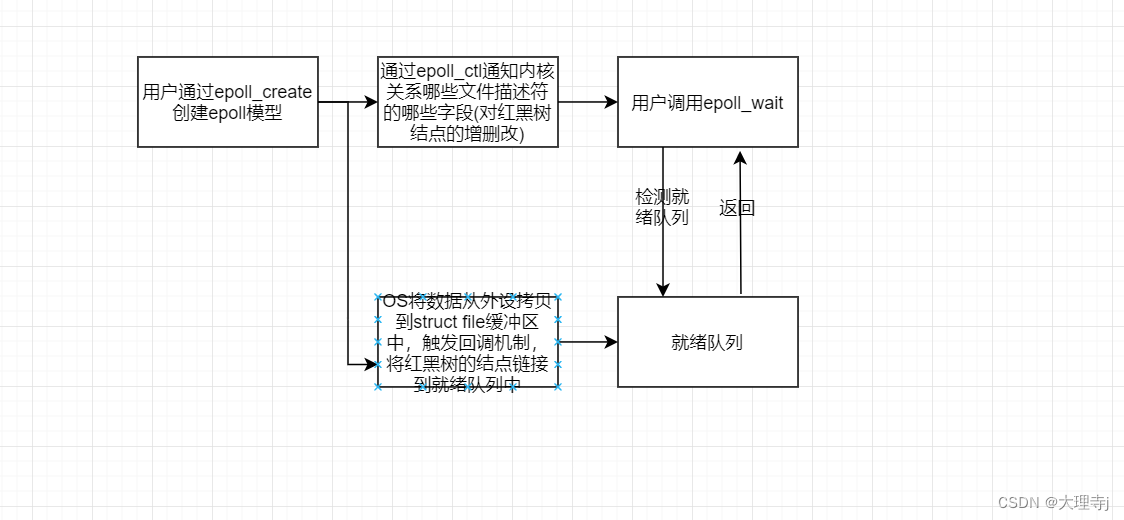
Linux-多路转接-epoll
epoll 接口认识epoll_createepoll_ctlepoll_wait epoll工作原理在内核中创建的数据结构epoll模型的一个完整工作流程 epoll工作模式LT-水平触发ET-边缘触发两种方式的对比 epoll的使用场景对于poll的改进惊群效应什么是惊群效应如何解决惊群效应原子操作/mutex/spinlock如何选择…...
Java面试被问了几个简单的问题,却回答的不是很好
作者:逍遥Sean 简介:一个主修Java的Web网站\游戏服务器后端开发者 主页:https://blog.csdn.net/Ureliable 觉得博主文章不错的话,可以三连支持一下~ 如有需要我的支持,请私信或评论留言! 前言 前几天参加了…...

概率论几种易混淆的形式
正态分布标准型 x − μ σ \frac{x - \mu}{\sigma} σx−μ 大数定律形式 P { X ≤ ∑ i 1 n x i − n μ n σ 2 } ∫ − ∞ X 1 2 π e − x 2 2 d x P\{X \le \frac{\sum_{i 1}^{n}x_i -n\mu}{\sqrt{n\sigma^2}} \} \int _{-\infty}^{X}\frac{1}{\sqrt{2\pi}}e^{-\fr…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
