当前位置： 首页 > news >正文

高并发系统 - 接口幂等技术方案，高可用系统架构与技术选型

news 2026/2/7 12:20:34

幂等概念来自于数学，在计算机科学中，幂等表示一次后、或多次请求某一资源，应该有同样的影响效果。
在业务表现上一般是同样的数据效果，下面就常用的业务场景，来聊聊幂等的技术方案。

----------------- 数据层 -----------------

  1. 索引与事务
    根据业务需要，给表添加唯一索性或组合索引，防止产生脏数据。
    根据数据库隔离级别，比如可重复读，在操作多表数据时，使用事务，要求数据要么全部操作成功，要么全部失败。
  2. 悲观锁
    根据实际情况使用，查询指定数据时指定用于更新，注意根据主键或唯一索引查询。数据锁定时间可能会很长，会造成读取该数据的等待时间长。
  3. 乐观锁
    乐观锁只在更新数据的那一刻锁表，适用于并发冲突不是很高的场景，可配合业务重试机制。
    乐观锁的实现方式，一般通过版本号或时间戳来实现，其他条件也可。
    之前的文章『MySQL锁与应用场景』，有说乐观锁与悲观锁的SQL示范。

----------------- 业务层 -----------------

  1. 对外提供的接口
    对接外部系统时，使用来源、业务流水号等，作为联合唯一索引，或者生成分布式唯一ID，记录在数据库。
    来请求时，查询数据库流水号已存在，并处理成功，就是重复请求，直接返回。如果数据不存在，记录流水号，开始处理，插入数据成功，接着返回成功。
  2. 先查询再插入
    对于并发不高的业务，为了支持重复执行，简单的处理方式是，查询关键数据来判断&

相关文章：

高并发系统 - 接口幂等技术方案，高可用系统架构与技术选型

幂等概念来自于数学，在计算机科学中，幂等表示一次后、或多次请求某一资源，应该有同样的影响效果。 在业务表现上一般是同样的数据效果，下面就常用的业务场景，来聊聊幂等的技术方案。 ----------------- 数据层 ----------------- 索引与事务 根据业务需要，给表添加唯一索…...

编程日记 2023/9/25 11:41:20

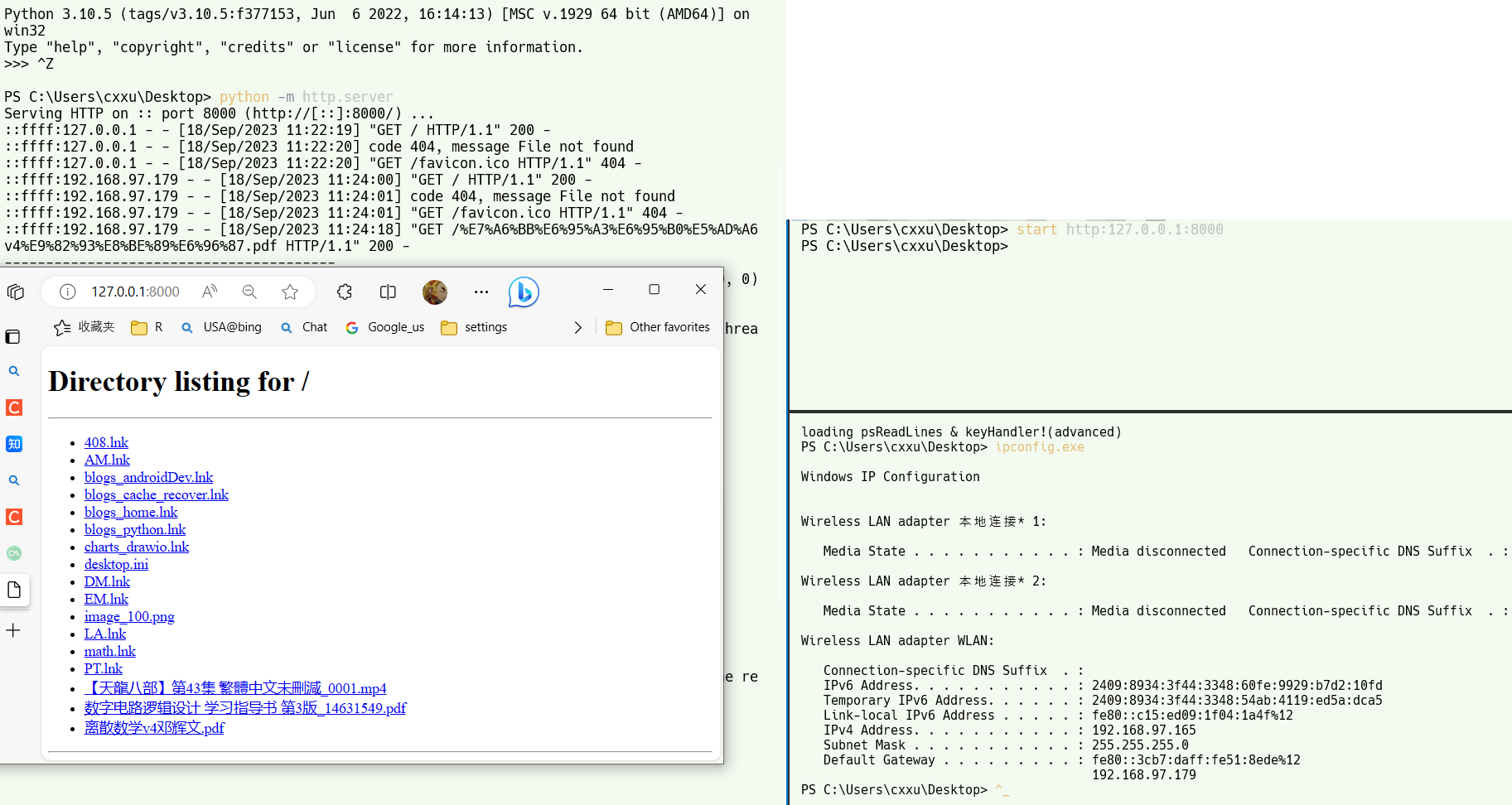
简单的手机电脑无线传输方案@固定android生成ftp的IP地址(android@windows)

文章目录 abstractwindows浏览android文件环境准备客户端软件无线网络链接步骤其他方法 手机浏览电脑文件公网局域网everythingpython http.server 高级:固定android设备IP准备检查模块是否生效 windows 访问ftp服务器快捷方式命令行方式双击启动方式普通快捷方式映射新的网络位…...

编程日记 2023/9/25 11:39:18

Unity3D 检测鼠标位置的Sprite像素颜色

思路 获取鼠标所在屏幕坐标(Vector2)通过相机ScreenToWorldPoint(Vector3)转为世界坐标 (注意Vector3的z是距离相机的距离，相机需要正交)通过SpriteRenderer访问边界Bounds通过Bounds.Contain检测世界坐标是否在SpriteBounds内通过比例计算来确定在Sprite内的UV坐标…...

编程日记 2023/9/25 11:38:17

layui input 监听事件

//监听表单单选框复选框选择 form.on(radio, function (data) { console.log(data.value); //得到被选中的值 }); //监听表单下拉菜单选择 form.on(select, function (data) { console.log(data.value); //得到被选中的值 }); //监听表单复选框选择 …...

编程日记 2023/9/25 11:37:15

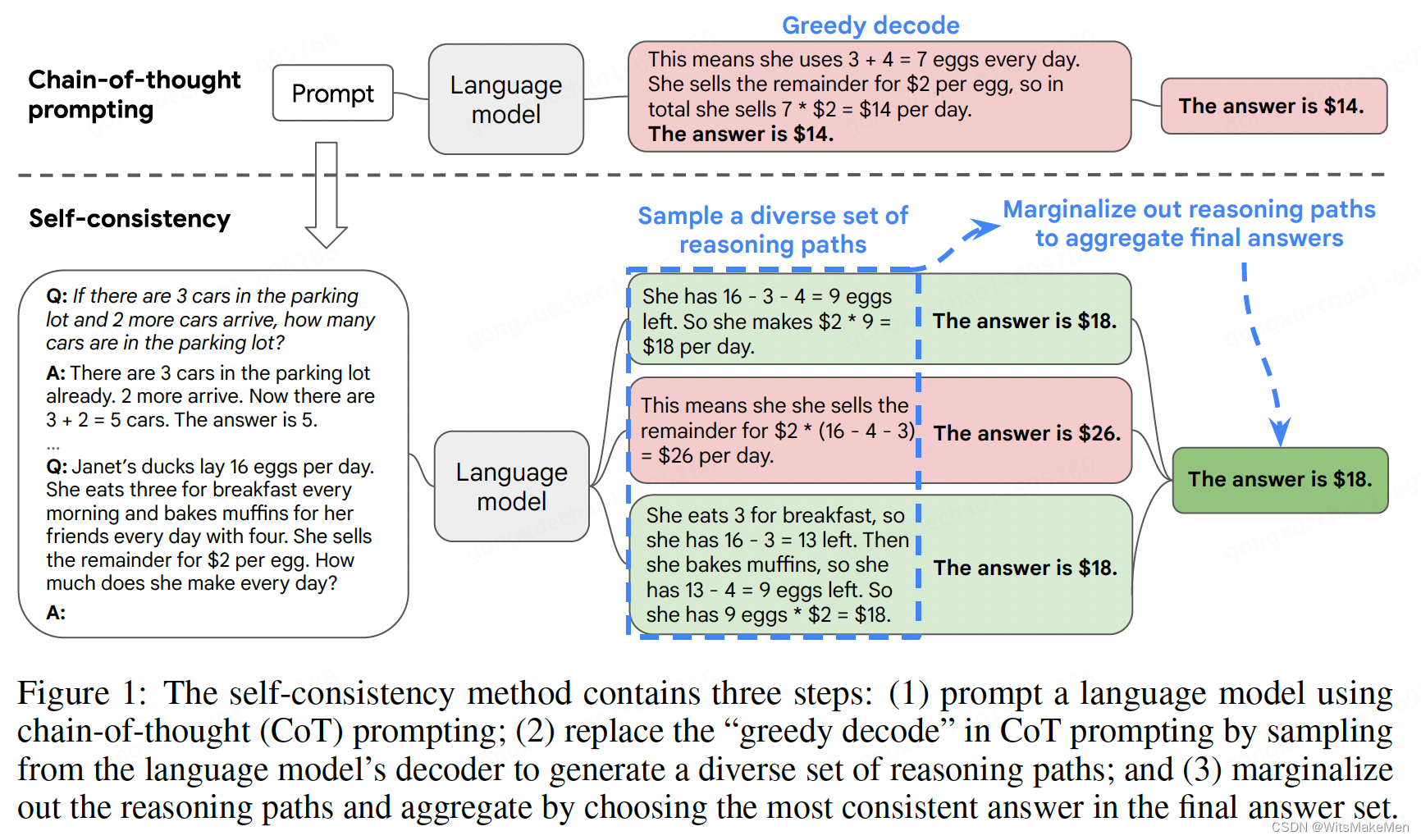
一致性思维链（SELF-CONSISTENCY IMPROVES CHAIN OF THOUGHT REASONING IN LANGUAGE MODELS）

概要 思维链已经在很多任务上取得了非常显著的效果，这篇论文中提出了一种 self-consistency 的算法，来代替 贪婪解码 算法。本方法通过 采样多个思维链集合，然后LLM模型生成后，选择一个最一致的答案作为最后的结果。一致性思维链…...

编程日记 2023/9/25 11:35:13

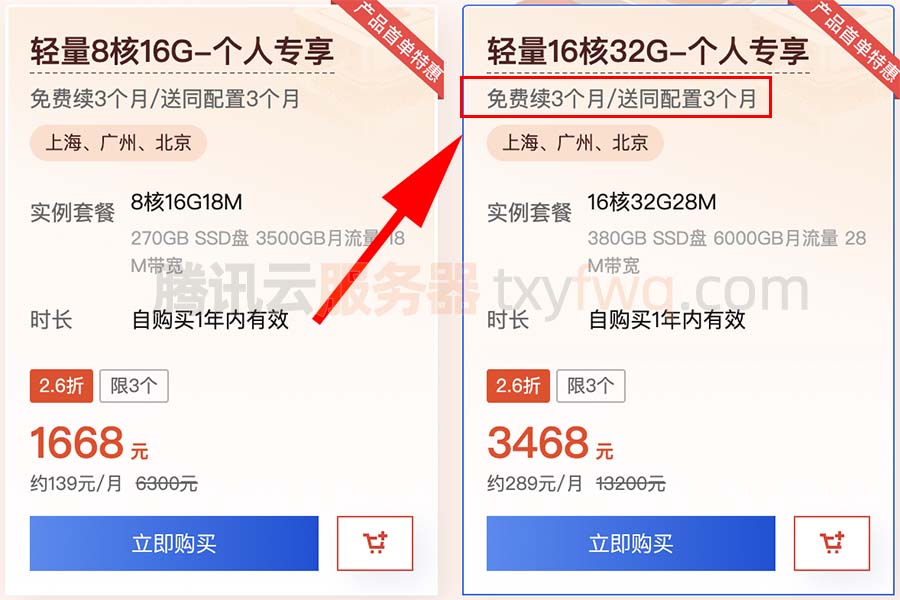
腾讯云16核服务器配置大全_16核CPU型号性能测评

腾讯云16核CPU服务器有哪些配置可以选择？可以选择标准型S6、标准型SA3、计算型C6或标准型S5等，目前标准型S5云服务器有优惠活动，性价比高，计算型C6云服务器16核性能更高，轻量16核32G28M带宽优惠价3468元15个月&#xf…...

编程日记 2023/9/25 11:33:11

HTML中Input elements should have autocomplete attributes的解决方案

kwfwservice.php:1 [DOM] Input elements should have autocomplete attributes (suggested: “current-password”): (More info: https://goo.gl/9p2vKq) <input name"password" id"password" lay-verify"required" placeholder"密码&…...

编程日记 2023/9/25 11:30:08

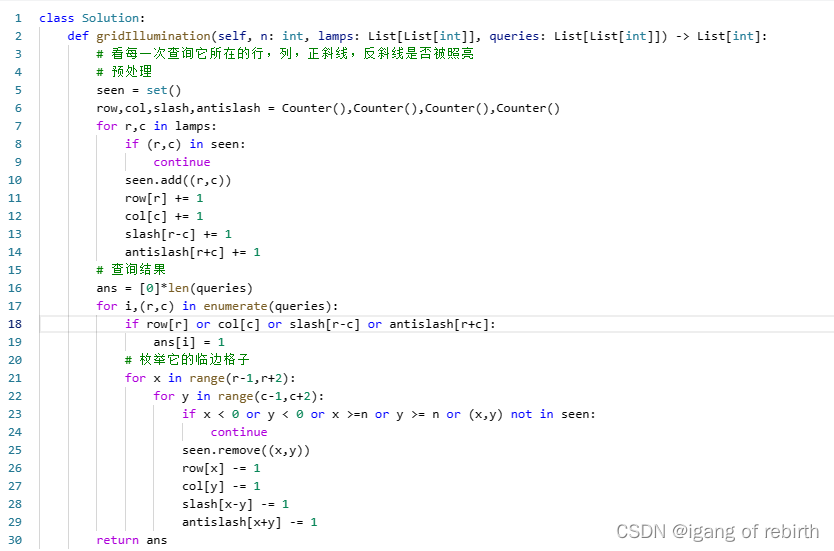
2808. 使循环数组所有元素相等的最少秒数；1015. 可被 K 整除的最小整数；1001. 网格照明

2808. 使循环数组所有元素相等的最少秒数 核心思想&#xff1a;枚举每个元素作为相等元素最多需要多少秒&#xff0c;然后维护它的最小值。最多需要多少秒是怎么计算的&#xff0c;我们可以把相等值的下标拿出来&#xff0c;然后你会发现两个相邻下标&#xff08;相邻下标只的…...

编程日记 2023/9/25 11:29:07

Python爬虫在Web应用自动化测试中的应用

在Web应用开发过程中&#xff0c;自动化测试是确保应用质量和稳定性的重要环节。本文将介绍如何使用Python爬虫与自动化测试技术相结合&#xff0c;实现对Web应用进行自动化测试的方法和步骤。通过这种结合&#xff0c;我们可以提高测试效率、减少人力成本&#xff0c;并确保应…...

编程日记 2023/9/25 11:28:06

苹果手机短信删除了怎么恢复？3种有效方法介绍

手机短信是一种即时通信方式&#xff0c;人们可以使用短信来达到快速传递信息的目的。在没有网络或者网络不稳定的时候&#xff0c;短信仍然可以做到发送和接收&#xff0c;这弥补了其他网络通信软件的缺点。 所以说&#xff0c;手机短信仍然是我们生活中不可缺少的一部分。当…...

编程日记 2023/9/25 11:26:04

前端JavaScript中的 == 和 ===区别，以及他们的应用场景，快来看看吧，积累一点知识。

&#x1f3ac; 江城开朗的豌豆&#xff1a;个人主页 &#x1f525; 个人专栏 :《 VUE 》 《 javaScript 》 ⛺️ 生活的理想&#xff0c;就是为了理想的生活 ! 目录 一、等于操作符 二、全等操作符 三、区别 小结 一、等于操作符 等于操作符用两个等于号&#xff08; &am…...

编程日记 2023/9/25 11:25:03

文献阅读：LIMA: Less Is More for Alignment

文献阅读&#xff1a;LIMA: Less Is More for Alignment 1. 内容简介2. 实验设计 1. 整体实验设计2. 数据准备3. 模型准备4. metrics设计 3. 实验结果 1. 基础实验2. 消解实验3. 多轮对话 4. 结论 & 思考 文献链接&#xff1a;https://arxiv.org/abs/2305.11206 1. 内容简…...

编程日记 2023/9/25 11:22:00

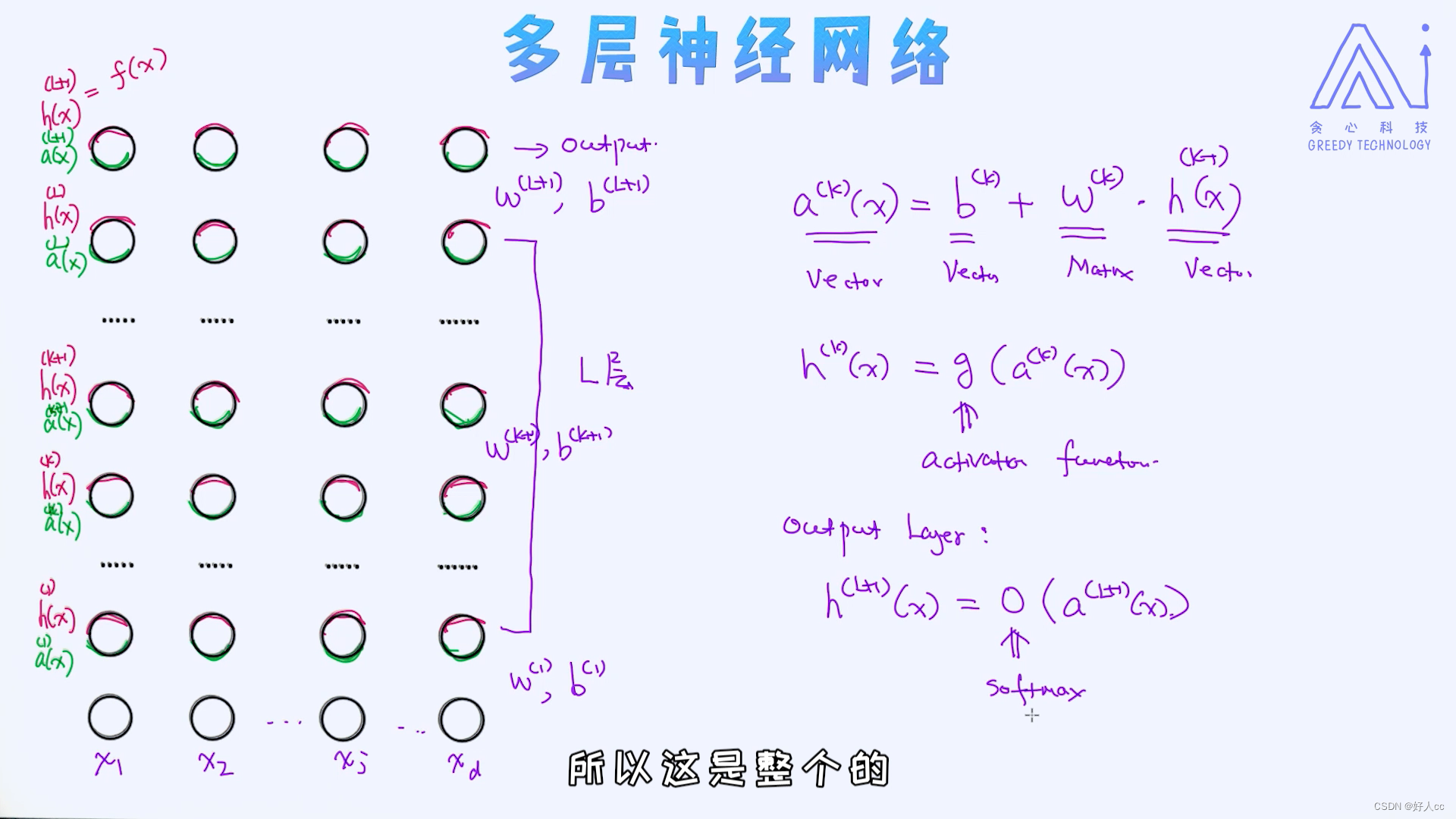
机器学习第十四课--神经网络

总结起来&#xff0c;对于深度学习的发展跟以下几点是离不开的: 大量的数据(大数据)计算资源(如GPU)训练方法(如预训练) 很多时候&#xff0c;我们也可以认为真正让深度学习爆发起来的是数据和算力&#xff0c;这并不是没道理的。 由于神经网络是深度学习的基础&#xff0c;学…...

编程日记 2023/9/25 11:20:59

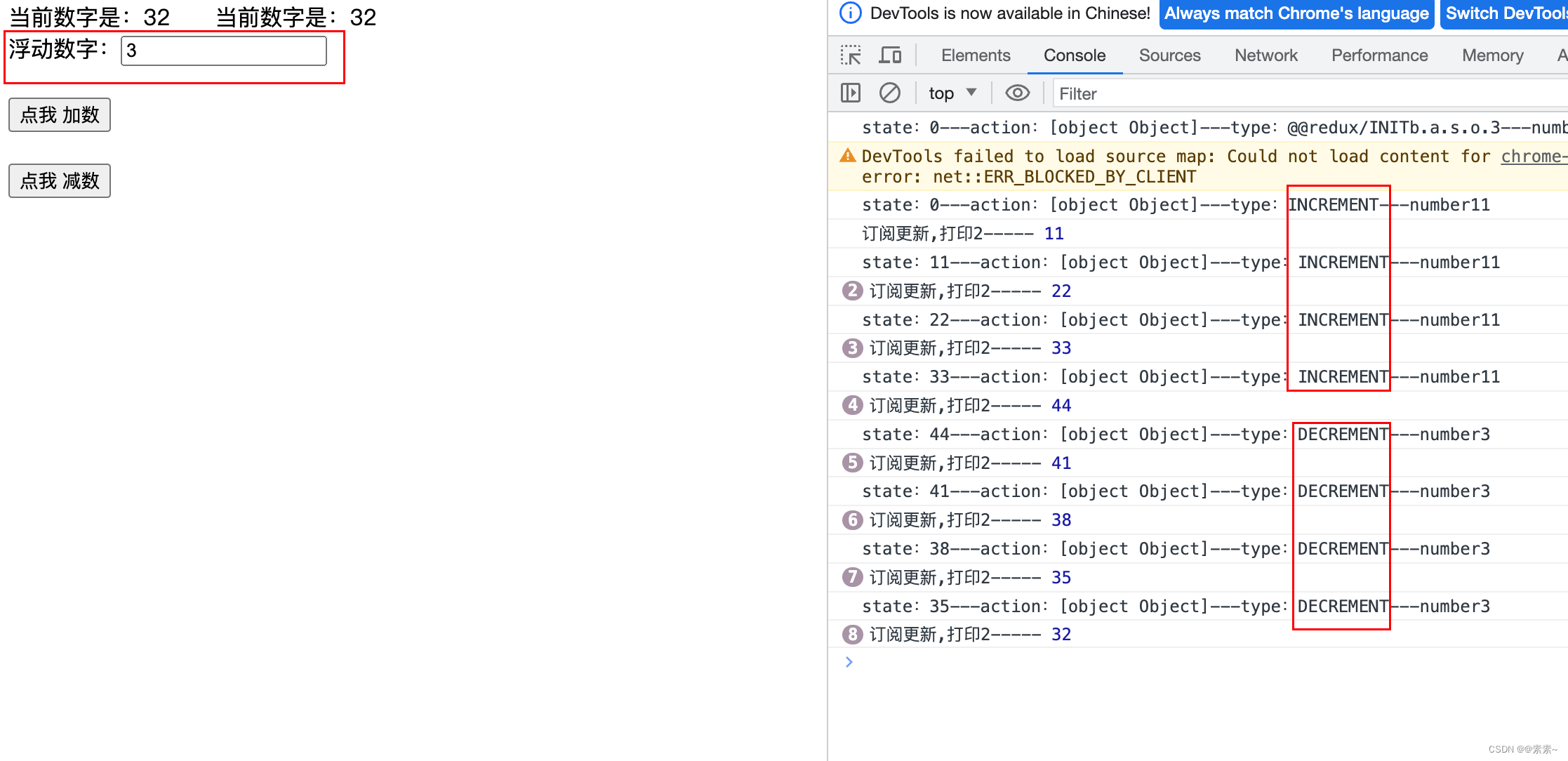
React（react18）中组件通信04——redux入门

React&#xff08;react18&#xff09;中组件通信04——redux入门 1. 前言1.1 React中组件通信的其他方式1.2 介绍redux1.2.1 参考官网1.2.2 redux原理图1.2.3 redux基础介绍1.2.3.1 action1.2.3.2 store1.2.3.3 reducer 1.3 安装redux 2. redux入门例子3. redux入门例子——优…...

编程日记 2023/9/25 11:18:56

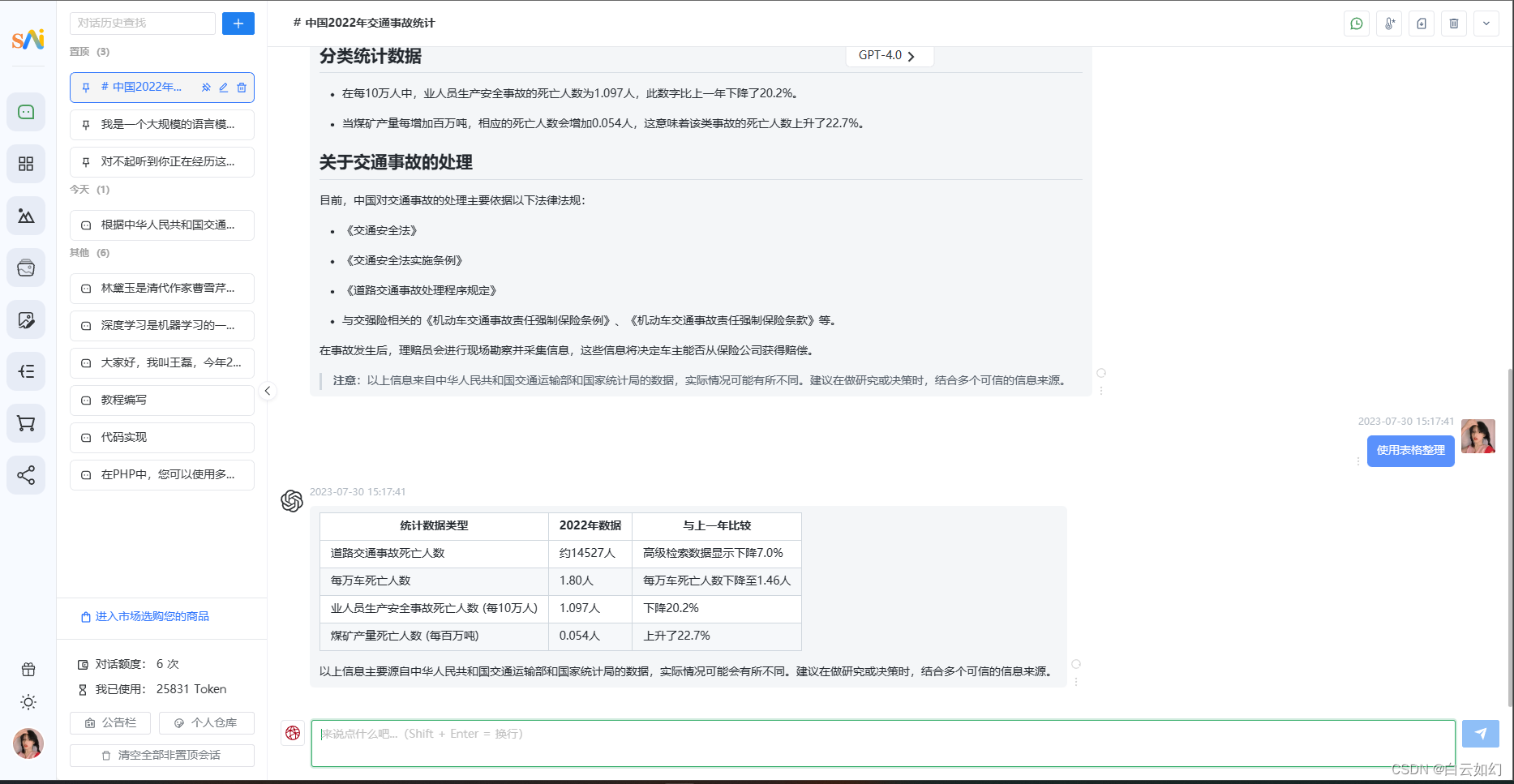
最新AI创作系统+ChatGPT网站源码+支持GPT4.0+支持ai绘画+支持国内全AI模型

一、AI创作系统 SparkAi系统是基于很火的GPT提问进行开发的Ai智能问答系统。本期针对源码系统整体测试下来非常完美&#xff0c;可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署AI创作ChatGPT系统&#xff1f;小编这里写一个详细图文教程吧&#x…...

编程日记 2023/9/25 11:15:54

react+umi项目中引入antd组件报错:“Button”不能用作 JSX 组件解决方案

具体报错信息 “Button”不能用作 JSX 组件。 Its type ‘(props: IProps) > React.ReactElement’ is not a valid JSX element type. 不能将类型“(props: IProps) > React.ReactElement”分配给类型“(props: any, deprecatedLegacyContext?: any) > ReactNode”。…...

编程日记 2023/9/25 11:13:52

常用算法模板

目录 快读、快输 快读、快输 #include <cstdio> #define Re register int #define LD double// 读整数 inline void in(Re &x) {int f 0; x 0; char c getchar();while (c < 0 || c > 9) f | c -, c getchar();while (c > 0 && c < 9) x …...

编程日记 2023/9/25 11:12:50

最全跨境独立站建站详细步骤解析

对于跨境电商卖家来说&#xff0c;无论是规避“鸡蛋放在同一个篮子里”的风险&#xff0c;还是追求更多的销售额和利润&#xff0c;多平台、多站点的布局都是其至关重要的战略。加之市场的变化带来了新的发展机遇&#xff0c;这也使得如今很多出海企业都在抢占独立站新风口。然…...

编程日记 2023/9/25 11:08:47

提升群辉AudioStation音乐体验，实现公网音乐播放

文章目录 本教程解决的问题是&#xff1a;按照本教程方法操作后&#xff0c;达到的效果是本教程使用环境&#xff1a;1 群晖系统安装audiostation套件2 下载移动端app3 内网穿透&#xff0c;映射至公网 很多老铁想在上班路上听点喜欢的歌或者相声解解闷儿&#xff0c;于是打开手…...

编程日记 2023/9/25 11:07:46

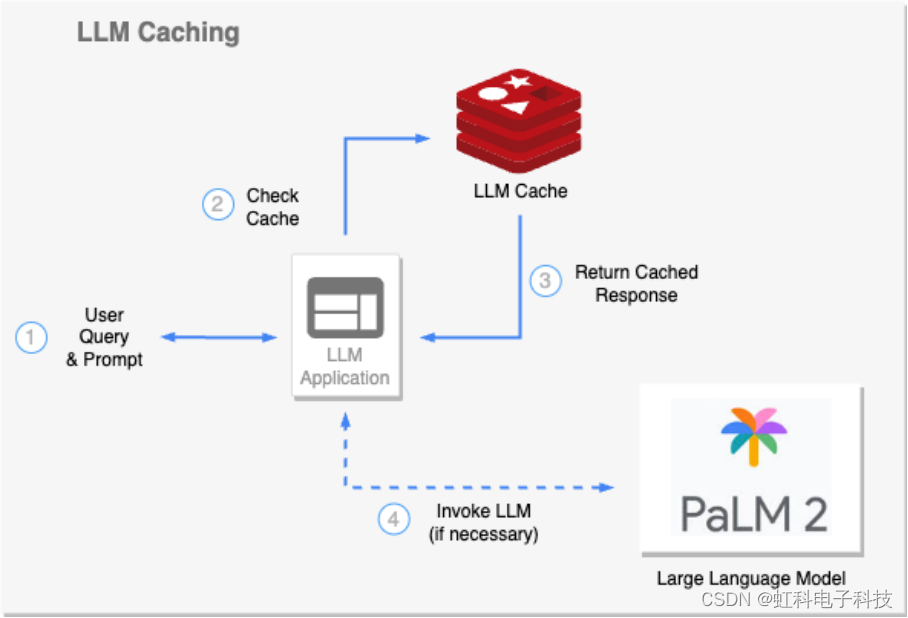
虹科分享 | 谷歌Vertex AI平台使用Redis搭建大语言模型

文章来源&#xff1a;虹科云科技 点此阅读原文 基础模型和高性能数据层这两个基本组件始终是创建高效、可扩展语言模型应用的关键&#xff0c;利用Redis搭建大语言模型&#xff0c;能够实现高效可扩展的语义搜索、检索增强生成、LLM 缓存机制、LLM记忆和持久化。有Redis加持的大…...

编程日记 2023/9/25 11:04:43

从零开始打造 OpenSTLinux 6.6 Yocto 系统（基于STM32CubeMX）（九）

设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile&#xff0c;新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

编程新知 2026/2/5 12:11:18

vue3 定时器-定义全局方法 vue+ts

1.创建ts文件 路径&#xff1a;src/utils/timer.ts 完整代码&#xff1a; import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

编程新知 2025/8/9 0:31:20

AI，如何重构理解、匹配与决策？

AI 时代&#xff0c;我们如何理解消费&#xff1f; 作者&#xff5c;王彬 封面&#xff5c;Unplash 人们通过信息理解世界。 曾几何时&#xff0c;PC 与移动互联网重塑了人们的购物路径&#xff1a;信息变得唾手可得&#xff0c;商品决策变得高度依赖内容。 但 AI 时代的来…...

编程新知 2026/1/30 2:33:11

JS设计模式(4)：观察者模式

JS设计模式(4):观察者模式 一、引入 在开发中&#xff0c;我们经常会遇到这样的场景&#xff1a;一个对象的状态变化需要自动通知其他对象&#xff0c;比如&#xff1a; 电商平台中&#xff0c;商品库存变化时需要通知所有订阅该商品的用户&#xff1b;新闻网站中&#xff0…...

编程新知 2025/9/1 6:48:07

Java编程之桥接模式

定义 桥接模式&#xff08;Bridge Pattern&#xff09;属于结构型设计模式&#xff0c;它的核心意图是将抽象部分与实现部分分离&#xff0c;使它们可以独立地变化。这种模式通过组合关系来替代继承关系&#xff0c;从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

编程新知 2026/1/23 10:28:48

GitFlow 工作模式（详解）

今天再学项目的过程中遇到使用gitflow模式管理代码&#xff0c;因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存&#xff0c;无论是github还是gittee&#xff0c;都是一种基于git去保存代码的形式&#xff0c;这样保存代码…...

编程新知 2026/1/26 12:37:40

在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）

考察一般的三次多项式&#xff0c;以r为参数&#xff1a; p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]&#xff1b; 此多项式的根为&#xff1a; 尽管看起来这个多项式是特殊的&#xff0c;其实一般的三次多项式都是可以通过线性变换化为这个形式…...

编程新知 2026/1/30 3:24:00

PostgreSQL——环境搭建

一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在&#xff0…...

编程新知 2025/11/26 20:46:42

c++第七天 继承与派生2

这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分&#xff1a;派生类构造函数与析构函数 当创建一个派生类对象时&#xff0c;基类成员是如何初始化的&#xff1f; 1.当派生类对象创建的时候&#xff0c;基类成员的初始化顺序 …...

编程新知 2026/2/2 21:55:02

小木的算法日记-多叉树的递归/层序遍历

&#x1f332; 从二叉树到森林&#xff1a;一文彻底搞懂多叉树遍历的艺术 &#x1f680; 引言 你好&#xff0c;未来的算法大神&#xff01; 在数据结构的世界里&#xff0c;“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的&#xff0c;它…...

编程新知 2025/11/13 14:22:52