《计算机视觉中的多视图几何》笔记(11)
11 Computation of the Fundamental Matrix F F F
本章讲述如何用数值方法在已知若干对应点的情况下求解基本矩阵 F F F。
文章目录
- 11 Computation of the Fundamental Matrix F F F
- 11.1 Basic equations
- 11.1.1 The singularity constraint
- 11.1.2 The minimum case – seven point correspondences
- 11.2 The normalized 8-point algorithm
- 11.3 The algebraic minimization algorithm
- 11.4 Geometric distance
- 11.4.1 黄金法则 (Gold Standard method)
- 11.4.2 Parametrization of rank-2 matrices
- 11.4.3 First-order geometric error (Sampson distance)
- 11.5 Experimental evaluation of the algorithms
- 11.6 Automatic computation of F F F
- 11.7 Special cases of F F F-computation
- 11.7.1 Pure translational motion
- 11.7.2 Planar motion
- 11.7.3 The calibrated case
- 11.8 Correspondence of other entities
- 11.9 Degeneracies
- 11.10 A geometric interpretation of F F F-computation
- 11.11 The envelope of epipolar lines
- 11.11.1 Verification of epipolar line covariance
- 11.12 Image rectification
- 11.12.1 Mapping the epipole to infinity
- 11.12.2 Matching transformations
- 11.12.3 Algorithm outline
- 11.12.4 Affine rectification
11.1 Basic equations
基本矩阵定义如下:
x ′ T F x = 0 x'^{T} F x = 0 x′TFx=0
其中 x x x和 x ′ x' x′为两张图片中的任意一对对应点。
定义 x = ( x , y , 1 ) T \bold{x} = (x,y,1)^{T} x=(x,y,1)T, x ′ = ( x ′ , y ′ , 1 ) T \bold{x'} = (x',y',1)^{T} x′=(x′,y′,1)T。带入基本矩阵的定义并整理可以得到一个方程组,记为 A f = 0 Af = 0 Af=0。
解析解: A A A的rank如果是8,那么直接求方程组的特解就可以。但是一般情况下有噪声,所以 A A A的rank有可能是9,那么就用SDV分解。可以表达成 A = U D V T A=UDV^{T} A=UDVT,那么 f f f就是 V V V的最后一列。

11.1.1 The singularity constraint
F F F是一个奇异矩阵,rank为2。利用这个性质,我们可以先用解析解求出一个 F F F,然后分解为 F = U D V T F=UDV^{T} F=UDVT,进一步写成 F = U d i a g ( r , s , t ) V T F=Udiag(r,s,t)V^{T} F=Udiag(r,s,t)VT,接着把 t t t换成0就可以了。利用解析解求 F F F的时候需要8组对应点,所以这个方法叫8点法。
11.1.2 The minimum case – seven point correspondences
求解 A f = 0 Af=0 Af=0,然后选基础解系中的两个特解 f 1 , f 2 f_1,f_2 f1,f2(书中叫零空间null space),然后构造一个方程 α f 1 + ( 1 − α ) f 2 \alpha f_1 + (1-\alpha )f_2 αf1+(1−α)f2,再利用 F F F是奇异矩阵的性质,得到 d e t ( α f 1 + ( 1 − α ) f 2 ) = 0 det(\alpha f_1 + (1-\alpha )f_2) = 0 det(αf1+(1−α)f2)=0,解这个方程就可以得到 α \alpha α。
11.2 The normalized 8-point algorithm
把8个点的质心平移到原点,把点看成一个向量,然后把向量模长归一化。
11.3 The algebraic minimization algorithm
优化目标:找到一个 F F F,使得 ∣ ∣ A f ∣ ∣ ||Af|| ∣∣Af∣∣最小,且满足 ∣ ∣ f ∣ ∣ = 1 ||f||=1 ∣∣f∣∣=1且 d e t F = 0 det F=0 detF=0。
步骤如下:
- 通过8点法找初始值 F 0 F_0 F0,然后找到 F 0 F_0 F0的零向量 e 0 e_0 e0
- 记 e 0 = e i e_0 = e_i e0=ei,通过 e i e_i ei构造 E i E_i Ei
E 0 = [ e 0 0 0 0 e 0 0 0 0 e 0 ] E_0 = \left[ \begin{matrix} e_0 & 0 & 0 \\ 0 & e_0 & 0 \\ 0 & 0 & e_0 \\ \end{matrix} \right] E0= e0000e0000e0 - 设 f i = E i m i f_i=E_i m_i fi=Eimi用P595的算法求解优化目标
- 计算误差 ϵ i = A f i \epsilon_i = A f_i ϵi=Afi
- 利用P600的Levenberg–Marquardt算法改变 e i e_i ei
- 重复1到5步直到算法收敛
11.4 Geometric distance
本节主要介绍如何用几何损失函数来计算基本矩阵。
11.4.1 黄金法则 (Gold Standard method)
我们假设图像噪声服从高斯分布,那么我们优化下式:
Σ i d ( x i , x ^ ) 2 + d ( x i ′ , x ^ ′ ) 2 \Sigma_i d(x_i,\hat{x})^2 + d(x_i^{'},\hat{x}^{'})^2 Σid(xi,x^)2+d(xi′,x^′)2
x i ↔ x i ′ x_i \leftrightarrow x^{'}_i xi↔xi′是已知对应点。 x ^ , x ^ ′ \hat{x},\hat{x}^{'} x^,x^′是没有噪声的点。
优化步骤如下:
- 根据含有噪声的点 x i , x i ′ x_i,x'_i xi,xi′估计出一个初始的 F ^ \hat{F} F^
- 根据 F ^ \hat{F} F^求出 e ′ e^{'} e′(回忆基本矩阵定义 F = [ e ′ ] × P ′ P + F=[e']_{\times}P'P^{+} F=[e′]×P′P+),然后构造 P = [ I ∣ 0 ] , P ′ = [ [ e ′ ] × F ^ ∣ e ′ ] P=[I|0],P'=[[e']_{\times}\hat{F}|e^{'}] P=[I∣0],P′=[[e′]×F^∣e′]
- 根据 x i ↔ x i ′ x_i \leftrightarrow x'_i xi↔xi′ 还有 F ^ \hat{F} F^,用三角化求出空间点 X ^ \hat{X} X^
- 根据 X ^ \hat{X} X^有以下两式成立: x i ^ = P X ^ , x i ^ ′ = P ′ X ^ \hat{x_i} = P\hat{X}, \hat{x_i}' = P'\hat{X} xi^=PX^,xi^′=P′X^
- 把上两式带入优化目标
11.4.2 Parametrization of rank-2 matrices
非线性优化要求把 F F F参数化,下面介绍几种方法:
- Over-parametrization 把 F F F写成 F = [ t ] × M F=[t]_{\times}M F=[t]×M M是任意的 3 × 3 3 \times 3 3×3 矩阵
- Epipolar parametrization 把 F F F 第三列写成前两列的线性组合
- Both epipoles as parameters 参见书P286的11.8式
11.4.3 First-order geometric error (Sampson distance)
Sampson distance以 x ′ F x i = 0 x^{'} F x_{i}=0 x′Fxi=0为优化目标,将其写成:
( x ′ F x i ) 2 ( F x i ) 1 2 + ( F x i ) 2 2 + ( F x i ′ ) 1 2 + ( F x i ′ ) 1 2 \frac{(x^{'} F x_{i})^2}{(Fx_i)^2_1 + (Fx_i)^2_2 + (Fx^{'}_i)^2_1 + (Fx^{'}_i)^2_1} (Fxi)12+(Fxi)22+(Fxi′)12+(Fxi′)12(x′Fxi)2
( F x i ) j 2 (Fx_i)^2_j (Fxi)j2 代表 F x i Fx_i Fxi的第 j j j个元素。
Symmetric epipolar distance
以 x ′ F x i = 0 x^{'} F x_{i}=0 x′Fxi=0为优化目标,那么我们可以让 x ′ x^{'} x′尽可能靠近 F x i F x_{i} Fxi.所以就有以下损失函数:
Σ d ( x ′ , F x i ) 2 + d ( x , F x i ′ ) 2 \Sigma d(x^{'},Fx_i)^2 + d(x,Fx_i^{'})^2 Σd(x′,Fxi)2+d(x,Fxi′)2
11.5 Experimental evaluation of the algorithms

本节选用3中不同的算法来进行对比:
- 正则化的8点法
- 最小化代数误差
- 最小化几何误差
我们直接上结论:
- 不要使用没有正则化的8点法,换句话说,用8点法必须要把点的坐标正则化
- 8点法是最快最方便的
- 如果追求准确,用最小化代数误差
- 用Sampson distance也非常好
11.6 Automatic computation of F F F
使用RANSAC的算法
其步骤如下:
-
先找出每幅图像中的特征点(SIFT, FAST, ORB)
-
计算特征点之间的对应
-
RANSAC采样:
- 任选7个点,用SVD解出一个 F F F
- 用 F F F和每一个点的坐标,计算一个距离 d ⊥ d_{\bot} d⊥. d ⊥ d_{\bot} d⊥可以选择重投影误差,或者Sampson。(多说一句,重投影误差就是指两次投影之间的差别,由于是同一个三维点的两次投影,这两次投影在理论上应该是一样的,所以误差应该为0.)
- 找出满足 d ⊥ < t d_{\bot} < t d⊥<t的点,其数量记为m,然后利用这些点重新计算 F F F,重复第二步,直到m足够多。
-
利用m对点,再选一个损失函数(比如说重投影和sampson),用Levenberg–Marquardt algorithm来优化这个损失函数
11.7 Special cases of F F F-computation
某些特殊的运动情况或部分已知的相机校准可以简化基本矩阵的计算。在每种情况下,基本矩阵的自由度数均小于一般运动情况下的7。我们举三个例子。
11.7.1 Pure translational motion
纯旋转情况下 F = [ e ′ ] × F = [e^{'}]_{\times} F=[e′]×这种情况下2对对应点就可以。

11.7.2 Planar motion
Planar motion意思是一个刚体沿着与某平面平行的方向( l s l_{s} ls)运动。在这种情况下 F F F满足 F = [ e ′ ] × [ l s ] × [ e ] × F=[e^{'}]_{\times} [l_{s}]_{\times} [e]_{\times} F=[e′]×[ls]×[e]×。
11.7.3 The calibrated case
如果相机已经标定了,那么我们可以在图像坐标系下计算本质矩阵 E E E,用 E E Ed代替 F F F,依旧是8点法。在E已知的情况下,把 E E E分解成 U D V T UDV^T UDVT,其中 D = d i a g ( a , b , c ) D = diag(a,b,c) D=diag(a,b,c),然后把 D D D换成 D ^ = d i a g ( ( a + b ) / 2 , ( a + b / 2 ) , 0 ) \hat{D} = diag((a+b)/2,(a+b/2),0) D^=diag((a+b)/2,(a+b/2),0),于是答案就是 E ^ = U D ^ V \hat{E} = U\hat{D}V E^=UD^V,知道了 E ^ \hat{E} E^和相机内参,就可以得出两个摄像机矩阵。
11.8 Correspondence of other entities
上文讲述的是我们用点对应的方法求解 F F F,本节我们介绍如何用其他对应方式来求解 F F F。
线段对应。线段对应不会给基本矩阵 F F F增加任何约束,因为线段重投影回去是平面,三维空间中平面一直会相交。
曲线对应。假设三维空间中有一条和极平面相切的曲线,该曲线投影在图像上的曲线一定和极线相切。这个性质就是一个约束:如果极线与图像中某曲线相切,则第二幅图像中对应的极线一定与某曲线相切。在这个结论里把曲线换成曲面也成立。
11.9 Degeneracies
退化的情况是指若干对对应点无法唯一确定基本矩阵 F F F,其具体细节如下:
定义 N N N为 A f = 0 Af=0 Af=0中 A A A的零空间,也就是该方程的特解。
补充一点基础知识:零空间的维度就是自由度。比如说解方程组 A f = 0 Af=0 Af=0的时候,方程的解里有3个自由变量,那么零空间的维数就是3( f f f本身是有9个变量)。
- dim(N) = 1,这种情况是对应点 n > 8 n>8 n>8,基本矩阵有唯一解
- dim(N) = 2,这种情况是对应点 n > 7 n>7 n>7,基本矩阵有1或3个解,主要会发生在对应点都落在某二次曲面上
- dim(N) = 3,这种情况是对应点 n > 6 n>6 n>6,基本矩阵有2个解系,主要会发生在两种情况:关于两个摄像机光心重合了,或者世界坐标中的点全部在一个平面上
11.10 A geometric interpretation of F F F-computation
几何解释就是 x ′ F x = 0 x'Fx = 0 x′Fx=0定义了四维空间中关于点 ( x , y , x ′ , y ′ ) (x,y,x',y') (x,y,x′,y′)的一个二次曲面。
11.11 The envelope of epipolar lines
基本矩阵的一个重要作用就是已知第一幅图中的某一点 x x x,找出第二幅图中该点对应的极线,那么第二幅途中 x x x的对应点 x ′ x^{'} x′肯定在极线上。如果我们考虑到噪声问题,那 x ′ x^{'} x′应该落在极线的附近。所以本节讲述如何用基本矩阵的协方差矩阵来决定 x ′ x^{'} x′的搜索区域。
我们直接上结论。 x x x代表一个点,对于基本矩阵 F F F,记其协方差矩阵 Σ F \Sigma_F ΣF, x x x对应的极线 l = F x l=Fx l=Fx, l l l的均值 m m m记为 l ˉ \bar{l} lˉ。
我们根据以上几项构建似然函数:
( l − m ) T Σ l ( l − m ) = k 2 (l-m)^T \Sigma_{l} (l-m) = k^2 (l−m)TΣl(l−m)=k2
k k k是某一个常数。同时我们用 F 2 ( x ) F_2(x) F2(x)代表 χ 2 2 \chi_2^2 χ22 分布。我们只需要把 k 2 k^2 k2带入 χ 2 2 \chi_2^2 χ22 分布,就可以得到要搜索的点落在 C 代表的区域内的概率。C如下所示:
C = l ˉ l ˉ T − k 2 Σ 1 C=\bar{l} {\bar{l}}^T -k^2\Sigma_1 C=lˉlˉT−k2Σ1
11.11.1 Verification of epipolar line covariance
本节主要验证一下上一节介绍方法的有效性。先找出一些对应点,当成ground truth。然后给每个点加上高斯噪声,然后再计算一个 F F F,通过 F F F求出极线,并且用上一节方法计算ground truth落在 c c c中的概率。
11.12 Image rectification
校正的意思是说把两个图像旋转到同一个平面,这样就是一对双目立体图像,可以做双目立体匹配。校正分为以下几个部分。
11.12.1 Mapping the epipole to infinity
把极点映射到无穷远,如果两幅图的极点都映射到了无穷远,那么他们的极线就平行了。极点本来是 ( f , 0 , 1 ) (f,0,1) (f,0,1),无穷远处的点是 ( f , 0 , 1 ) (f,0,1) (f,0,1), 我们有以下矩阵可以做到这一点:
G = [ 1 0 1 0 1 0 − 1 / f 0 1 ] G=\left[ \begin{matrix} 1 & 0 & 1\\ 0 & 1 & 0\\ -1/f & 0 & 1 \\ \end{matrix} \right] G= 10−1/f010101
如果考虑任意一点 x 0 x_0 x0,那么 G G G应该变成 G R T GRT GRT。 T T T把 x 0 x_0 x0转换到原点, R R R把 e ′ e^{'} e′旋转到 ( f , 0 , 1 ) (f,0,1) (f,0,1)。
11.12.2 Matching transformations
在上一节我们把一个图像已经转选转了某一个角度 (矩阵 H H H做了这个事),使其极线平行与立体匹配的基线,接下来我们需要把另外一个图像也转一下 (矩阵 H ′ H^{'} H′做这事),使其极线也平行与基线。我们不是对第二幅图像重复上一节,而是寻找 H H H和 H ′ H^{'} H′的关系。该关系描述如下:
如果 l l lhe l ′ l^{'} l′是两幅图像中对应的极线,那么有下式成立: H − T l = H ′ − T l ′ H^{-T}l=H'^{-T}l' H−Tl=H′−Tl′( H H H如果是点变换 H − T H^{-T} H−T就是线变换)。根据该式我们有以下优化函数:
Σ i d ( H x i , H ′ x i ′ ) 2 \Sigma_{i} d(Hx_i,H'x'_{i})^2 Σid(Hxi,H′xi′)2
同时, H H H和 H ′ H^{'} H′应当满足如下关系:
H = ( I + H ′ E ′ a T ) H ′ M H=(I+H^{'}E^{'}a^{T})H^{'}M H=(I+H′E′aT)H′M
其证明参见P306。
如果我们考虑一个特殊的 H ′ H^{'} H′,它可以把 e ′ e^{'} e′变换到无穷远点 ( 1 , 0 , 0 ) T (1,0,0)^T (1,0,0)T,(上文提到的 H ′ H^{'} H′没有这个性质),那么 H H H和 H ′ H^{'} H′ 应该有如下性质:在已知 F = [ e ′ ] × M F=[e^{'}]_{\times}M F=[e′]×M的条件下, H = H A H 0 H=H_A H_0 H=HAH0, H 0 = H ′ M H_0=H^{'}M H0=H′M, H A H_A HA是一个仿射变换。
利用这个性质,我们做一点改写: X ^ ′ = H ′ X i ′ \hat{X}^{'} = H^{'}X_i^{'} X^′=H′Xi′, X i ^ = H 0 X i \hat{X_i} = H_0X_i Xi^=H0Xi,
则优化目标可以变成:
Σ i d ( H A X i ^ , X i ′ ^ ) 2 \Sigma_i d(H_A\hat{X_i},\hat{X^{'}_i})^2 Σid(HAXi^,Xi′^)2
接下来我们参数化,令 X i ^ = ( x i ^ , y i ^ , 1 ) \hat{X_i}=(\hat{x_i},\hat{y_i},1) Xi^=(xi^,yi^,1), X i ′ ^ = ( x i ′ ^ , y i ′ ^ , 1 ) \hat{X^{'}_i}=(\hat{x^{'}_i},\hat{y^{'}_i},1) Xi′^=(xi′^,yi′^,1),以上优化目标就变成了:
Σ i ( a x i ^ + b y i ^ + c − x i ′ ^ ) 2 + ( y i ^ − y ′ ^ ) \Sigma_i (a\hat{x_i}+b\hat{y_i}+c-\hat{x^{'}_i})^{2} + (\hat{y_i}-\hat{y^{'}}) Σi(axi^+byi^+c−xi′^)2+(yi^−y′^)
11.12.3 Algorithm outline
本节对算法本身做一个总体的描述:
- 找出至少7对对应点
- 计算基本矩阵 F F F和两个极点 e , e ′ e,e' e,e′
- 找出 H ′ H^{'} H′,该矩阵把 e ′ e' e′映射到 ( 1 , 0 , 0 ) T (1,0,0)^T (1,0,0)T
- 优化目标函数 Σ d ( H x i , H ′ x ′ ) \Sigma d(Hx_i,H'x') Σd(Hxi,H′x′)
- 利用 H H H和 H ′ H' H′分别将两幅图像转换
11.12.4 Affine rectification
如果摄像机本身可以本仿射摄像机近似,那么就直接用仿射变换来校正,把上文的基本矩阵换成仿射相机的基本矩阵就可以。
相关文章:

《计算机视觉中的多视图几何》笔记(11)
11 Computation of the Fundamental Matrix F F F 本章讲述如何用数值方法在已知若干对应点的情况下求解基本矩阵 F F F。 文章目录 11 Computation of the Fundamental Matrix F F F11.1 Basic equations11.1.1 The singularity constraint11.1.2 The minimum case – sev…...
UE5 ChaosVehicles载具研究
一、基本组成 载具Actor类名称:WheeledVehiclePawn Actor最原始的结构 官方增加了两个摇臂相机,可以像驾驶游戏那样切换多机位、旋转观察 选择骨骼网格体、动画蓝图类、开启物理模拟 二、SportsCar_Pawn 角阻尼:物体旋转的阻力。数值越大…...
数据通信——应用层(域名系统)
引言 TCP到此就告一段落,这也意味着传输层结束了,紧随其后的就是TCP/IP五层架构的应用层。操作系统、编程语言、用户的可视化界面等等都要通过应用层来体现。应用层和我们息息相关,我们使用电子设备娱乐或办公时,接触到的就是应用…...

Visual Studio 更新:远程文件管理器
Visual Studio 中的远程文件管理器可以用来访问远程机器上的文件和文件夹,通过 Visual Studio 自带的连接管理器,可以实现不离开开发环境直接访问远程系统,这确实十分方便。 自从此功能发布以来,VS 开发团队努力工作,…...
ChatGPT追祖寻宗:GPT-3技术报告要点解读
论文地址:Language Models are Few-Shot Learners 往期相关文章: ChatGPT追祖寻宗:GPT-1论文要点解读_五点钟科技的博客-CSDN博客ChatGPT追祖寻宗:GPT-2论文要点解读_五点钟科技的博客-CSDN博客 本文的标题之所以取名技术报告而不…...

java easyexcel 导出多级表头
maven <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>${easyexcel.version}</version> </dependency> 导出行的对象 import com.alibaba.excel.annotation.ExcelIgnore; import …...

rar格式转换zip格式,如何做?
平时大家压缩文件时对压缩包格式可能没有什么要求,但是,可能因为工作需要,我们要将压缩包格式进行转换,那么我们如何将rar格式转换为其他格式呢?方法如下: 工具:WinRAR 打开WinRAR,…...

Java中的构造方法
在Java中,构造方法是类的特殊方法,用于初始化对象的实例变量和执行其他必要的操作,以便使对象能够正确地工作。构造方法与类同名,没有返回类型,并且在创建对象时自动调用。 以下是构造方法的一些基本特性:…...

【Java】fastjson
Fastjson简介 Fastjson是阿里巴巴的团队开发的一款Java语言实现的JSON解析器和生成器,它具有简单易用、高性能、高可用性等优点,适用于Java开发中的数据解析和生成。Fastjson的主要特点包括: 简单易用:Fastjson提供了简单易用的…...
JMeter之脚本录制
【软件测试面试突击班】如何逼自己一周刷完软件测试八股文教程,刷完面试就稳了,你也可以当高薪软件测试工程师(自动化测试) 前言: 对于一些JMeter初学者来说,录制脚本可能是最容易掌握的技能之一。…...

计算机网络的相关知识点总结
1.谈一谈对OSI七层模型和TCP/IP四层模型的理解? 不管是OSI七层模型亦或是TCP/IP四层模型,它们的提出都有一个共同的目的:通过分层来将复杂问题细化,通过各个层级之间的相互配合来更好的解决计算机中出现的问题。 说到分层…...

WPF实现轮播图(图片、视屏)
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
【Vue.js】使用Element搭建首页导航左侧菜单
目录 Mock.js 是什么 有什么好处 安装mockjs 编辑 引入mockjs mockjs使用 login-mock Bus事物总线 首页导航栏与左侧菜单搭建 结合总线完成组件通讯 Mock.js 是什么 Mock.js是一个用于生成随机数据的模拟数据生成器。它可以帮助开发人员模拟接口请求,生…...
Spring MVC常见面试题
Spring MVC简介 Spring MVC框架是以请求为驱动,围绕Servlet设计,将请求发给控制器,然后通过模型对象,分派器来展示请求结果视图。简单来说,Spring MVC整合了前端请求的处理及响应。 Servlet 是运行在 Web 服务器或应用…...
Java基础面试题精选:深入探讨哈希表、链表和接口等
目录 1.ArrayList和LinkedList有什么区别?🔒 2.ArrayList和Vector有什么区别?🔒 3.抽象类和普通类有什么区别?🔒 4.抽象类和接口有什么区别?🔒 5.HashMap和Hashtable有什么区别&…...
Spark计算框架
Spark计算框架 一、Spark概述二、Spark的安装部署(安装部署Spark的Cluster Manager-资源调度管理器的)1、Spark的安装模式1.1、Spark(单节点)本地安装1.2 Spark的Standalone部署模式的伪分布式安装1.3Spark的YARN部署模式1.4Spark…...

mybatis缓存源码分析
mybatis缓存源码分析 背景 在java程序与数据库交互的过程中永远存在着性能瓶颈,所以需要一直进行优化.而我们大部分会直接将目标放到数据库优化,其实我们应该先从宏观上去解决问题进而再去解决微观上的问题.性能瓶颈体现在什么地方呢?第一网络通信开销,网络数据传输通信.…...

机房小探索
现在连不了NJU-WLAN,怀疑是没有插网线,可以考虑买个USB转网卡的接口,但是我的电脑只有两个USB插口,还不知道版本是什么,之后还想连鼠标跟键盘外设呢。只能连NJU_SWI_WLAN,合理怀疑是Software Internet的缩写…...

PHP8的类与对象的基本操作之成员变量-PHP8知识详解
成员变量是指在类中定义的变量。在类中可以声明多个变量,所以对象中可以存在多个成员变量,每个变量将存储不同的对象属性信息。 例如以下定义: public class Goods { 关键字 $name; //类的成员变量 }成员属性必须使用关键词进行修饰…...
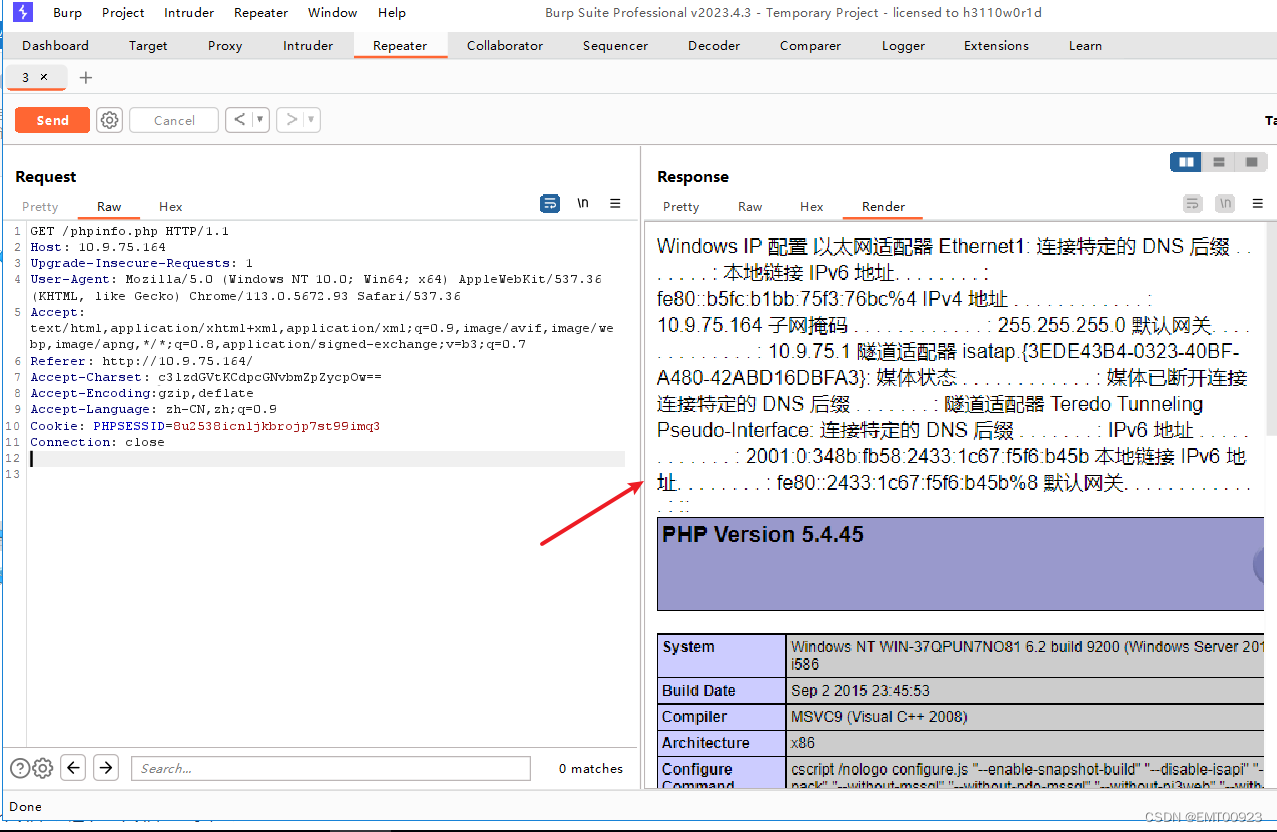
phpstudy2016 RCE漏洞验证
文章目录 漏洞描述漏洞验证 漏洞描述 PHPStudyRCE(Remote Code Execution),也称为phpstudy_backdoor漏洞,是指PHPStudy软件中存在的一个远程代码执行漏洞。 漏洞验证 打开phpstudy2016,用bp自带的浏览器访问www目录下…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...
