【李沐深度学习笔记】线性回归
课程地址和说明
线性回归p1
本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。
线性回归
如何在美国买房(经典买房预测问题)

一个简化的模型

线性模型

其中,
- x → = [ x 1 , x 2 , … , x i , … , x n ] T \overrightarrow {x}=\left [ x_{1},x_{2},\dots ,x_{i} ,\dots ,x_{n}\right ]^{T} x=[x1,x2,…,xi,…,xn]T, i i i代表第 i i i个特征(即本例中的卧室个数,卫生间个数和居住面积),其实为了方便记录第 j j j个样本的第 i i i个特征,我更倾向于这个写法: x j → = [ x j 1 , x j 2 , … , x j i , … , x j n ] T \overrightarrow {{x}_{j}}=\left [ x_{j}^{1},x_{j}^{2},\dots ,x_{j}^{i} ,\dots ,x_{j}^{n}\right ]^{T} xj=[xj1,xj2,…,xji,…,xjn]T,其中 j j j代表第 j j j个样本, i i i代表第 j j j个样本的第 i i i个特征,下面的章节这样写比较方便;
- w → = [ w 1 , w 2 , … , w i , … , w n ] T \overrightarrow {w}=\left [ w_{1},w_{2},\dots ,w_{i} ,\dots ,w_{n}\right ]^{T} w=[w1,w2,…,wi,…,wn]T, w i w_{i} wi是代表着第 i i i个特征的重要程度(即权重),假如卧室个数 x 1 x_{1} x1比卫生间个数 x 2 x_{2} x2的重要程度大,则 w 1 > w 2 w_{1}>w_{2} w1>w2;
- b b b代表着模型的标量偏差。
【提问】解释一下线性回归模型的标量偏差
【chatGPT回答】线性回归模型中的标量偏差(scalar bias)通常是指模型中的一个额外参数,用来调整模型的输出,使其更好地拟合数据。这个偏差值是一个常数,不依赖于输入特征,它在线性回归模型中起到平移或偏移输出的作用。
线性回归模型用于建立输入特征和输出目标之间的关系,通常表示为:
y = w x + b y = wx + b y=wx+b
其中:
- y y y 是模型的输出(预测值)。
- x x x 是输入特征。
- w w w 是特征的权重或系数,用来衡量特征对输出的影响。
- b b b 是标量偏差,也称为截距或偏移项,它表示当输入特征 (x) 为零时,模型的输出 (y) 的期望值。
标量偏差 (b) 允许模型在没有输入特征的情况下仍然能够有一个非零的输出。这对于捕捉数据中的整体偏移或平移是很重要的。例如,如果你正在建立一个房价预测模型,特征 (x) 可能表示房屋的大小,但即使房屋大小为零,房价也不应该为零,因此标量偏差 (b) 允许模型预测一个基本价格。
在训练线性回归模型时,模型会尝试学习最佳的权重 (w) 和偏差 (b) 的值,以最小化预测值与真实值之间的差距(损失函数)。这个过程通常使用最小二乘法来完成。
总之,线性回归模型的标量偏差是一个用来平移或偏移模型输出的常数参数,它允许模型在没有输入特征时仍能够产生非零的输出,从而更好地拟合数据。
- 加权和(也就是预测值): y = w 1 x 1 + w 2 x 2 + ⋯ + w n x n + b = [ w 1 w 2 … w n ] ⋅ [ x 1 x 2 … x n ] = < w → , x → > + b y=w_{1}x_{1}+w_{2}x_{2}+\dots+w_{n}x_{n}+b=\begin{bmatrix} w_{1} & w_{2} & \dots & w_{n} \end{bmatrix}\cdot \begin{bmatrix} x_{1} \\ x_{2} \\ \dots \\ x_{n} \end{bmatrix}=<\overrightarrow {w},\overrightarrow {x}>+b y=w1x1+w2x2+⋯+wnxn+b=[w1w2…wn]⋅ x1x2…xn =<w,x>+b,其中 < w → , x → > <\overrightarrow {w},\overrightarrow {x}> <w,x>为 w → \overrightarrow {w} w与 x → \overrightarrow {x} x的内积,内积符号表示中两个向量的位置可以换的,即 < w → , x → > = < x → , w → > <\overrightarrow {w},\overrightarrow {x}>=<\overrightarrow {x},\overrightarrow {w}> <w,x>=<x,w>,其实我更喜欢将预测值记为 y ^ = < w → , x → > + b \hat {y}=<\overrightarrow {w},\overrightarrow {x}>+b y^=<w,x>+b,后面会看到我为什么这样记录。
线性模型可以看做是单层神经网络

神经网络源于神经科学

衡量预估质量


训练数据

其中,
- 矩阵 X \bm{X} X的每一个行向量 x i → T , i = 1 , 2 , … , n \overrightarrow {x_{i}}^{T},i=1,2,\dots ,n xiT,i=1,2,…,n都代表着第 i i i个样本,本来 x i → \overrightarrow {x_{i}} xi都是列向量,但是 X = [ x 1 → , x 2 → , … , x i → , … , x n → ] T = [ x 1 → T x 2 → T ⋮ x i → T ⋮ x n → T ] \bm{X}=\left [ \overrightarrow {x_{1}},\overrightarrow {x_{2}},\dots ,\overrightarrow {x_{i}} ,\dots ,\overrightarrow {x_{n}}\right ]^{T}=\begin{bmatrix} \overrightarrow {x_{1}}^{T} \\ \overrightarrow {x_{2}}^{T}\\ \vdots \\ \overrightarrow {x_{i}}^{T} \\ \vdots \\ \overrightarrow {x_{n}}^{T} \end{bmatrix} X=[x1,x2,…,xi,…,xn]T= x1Tx2T⋮xiT⋮xnT ,所以 x i → T \overrightarrow {x_{i}}^{T} xiT与 x i → \overrightarrow {x_{i}} xi都代表第 i i i个样本,其样本向量中的各个分量即是这第 i i i个样本的各个特征;
- y → = [ y 1 , y 2 , … , y i , … , y n ] T \overrightarrow{y}=\left [ y_{1},y_{2},\dots ,y_{i} ,\dots ,y_{n}\right ]^{T} y=[y1,y2,…,yi,…,yn]T代表了所有真实值(本例为真实房价)的数据集合,其中 y i , i = 1 , 2 , … , n y_{i},i=1,2,\dots ,n yi,i=1,2,…,n代表第 i i i个样本 x i → \overrightarrow {x_{i}} xi对应的真实值。
参数学习

其中
- 根据上面提到的平方损失的定义,训练损失函数写为:
ℓ ( X , y → , w → , b ) = 1 2 n ∑ i = 1 n ( y i − y ^ i ) 2 = 1 2 n ∑ i = 1 n ( y i − ( ( < w → , x i → > + b ) ) ) 2 = 1 2 n ∑ i = 1 n ( y i − < w → , x i → > − b ) 2 \ell (\textbf{X},\overrightarrow {y},\overrightarrow {w},b)=\frac{1}{2n}\sum\limits_{i=1}^{n} \left ( y_{i}-\hat{y}_{i} \right )^{2}=\frac{1}{2n}\sum\limits_{i=1}^{n} \left ( y_{i}-((<\overrightarrow {w},\overrightarrow {x_{i}}>+b)) \right )^{2} =\frac{1}{2n}\sum\limits_{i=1}^{n} \left ( y_{i}-<\overrightarrow {w},\overrightarrow {x_{i}}>-b \right )^{2} ℓ(X,y,w,b)=2n1i=1∑n(yi−y^i)2=2n1i=1∑n(yi−((<w,xi>+b)))2=2n1i=1∑n(yi−<w,xi>−b)2
图中的 b b b应为 b → = ( b , b , . . . , b ) n × 1 T \overrightarrow {b}=(b,b,...,b)^{T}_{n\times 1} b=(b,b,...,b)n×1T,否则不符合数学上的定义,李沐老师之所以这么写是因为在PyTorch中,向量减去标量相当于对向量的每一个分量都减去相同的标量,所以上述公式在写代码时可以直接用,以下给出我推导的过程:

- a r g arg arg表示的是取什么什么值, a r g m i n arg min argmin指的是取最小值,图中的意思是找到使得损失函数 ℓ ( X , y → , w → , b ) \ell (\textbf{X},\overrightarrow {y},\overrightarrow {w},b) ℓ(X,y,w,b)的参数 w → ∗ , b ∗ \overrightarrow {w}^{*},b^{*} w∗,b∗.
显示解
因为我们用的是线性模型,所以我们有显示解。

【注】在评论区发现李沐老师少写了个转置,这里直接更正一下
将 X \bm{X} X进行增广, w → \overrightarrow {w} w进行增广,最终变为 X n × ( m + 1 ) , w → ( m + 1 ) × 1 \bm{X}_{n\times (m+1)},\overrightarrow {w}_{(m+1)\times 1} Xn×(m+1),w(m+1)×1,则变为:

由链式求导法则和公式当 y = ∣ ∣ x → ∣ ∣ 2 = ( ∑ i = 1 m x i 2 ) 2 = ( x 1 2 + x 2 2 + ⋯ + x m 2 ) 2 = x 1 2 + x 2 2 + ⋯ + x m 2 y=||\overrightarrow x||^2=(\sqrt{\sum\limits_{i=1}^{m} x_{i}^{2}})^{2}=(\sqrt{x_{1}^{2}+x_{2}^{2}+\dots +x_{m}^{2}})^{2}=x_{1}^{2}+x_{2}^{2}+\dots +x_{m}^{2} y=∣∣x∣∣2=(i=1∑mxi2)2=(x12+x22+⋯+xm2)2=x12+x22+⋯+xm2时,有:
∂ y ∂ x → = [ ∂ f ( x → ) ∂ x 1 ∂ f ( x → ) ∂ x 2 ⋮ ∂ f ( x → ) ∂ x m ] m × 1 = [ 2 x 1 2 x 2 ⋮ 2 x m ] m × 1 = 2 x → \frac{\partial {y}}{\partial\overrightarrow x}=\begin{bmatrix} \frac{\partial {f(\overrightarrow x)}}{\partial{x_{1}}}\\ \frac{\partial {f(\overrightarrow x)}}{\partial{x_{2}}}\\ \vdots \\ \frac{\partial {f(\overrightarrow x)}}{\partial{x_{m}}} \end{bmatrix}_{m\times 1}=\begin{bmatrix} 2x_{1}\\ 2x_{2}\\ \vdots \\ 2x_{m} \end{bmatrix}_{m\times 1}=2\overrightarrow x ∂x∂y= ∂x1∂f(x)∂x2∂f(x)⋮∂xm∂f(x) m×1= 2x12x2⋮2xm m×1=2x
可知,

总结

相关文章:

【李沐深度学习笔记】线性回归
课程地址和说明 线性回归p1 本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。 线性回归 如何在美国买房(经典买房预测问题) 一个简化的模型 线性模型 其中, x → [ x 1 , x 2 ,…...
微信收款码费率0.38太坑了
作为一个有多年运营经验的商家,我本人在申请收款功能时曾经走过了不少弯路。我找遍了市面上的知名的支付公司,但了解到的收款手续费率通常都在0.6左右,最低也只能降到0.38。这个过程吃过不少苦头。毕竟,收款功能是我们商家的命脉&…...

【学习笔记】CF1103D Professional layer
首先分析不出啥性质,所以肯定是暴力优化😅 常见的暴力优化手段有均摊,剪枝,数据范围分治(points),答案值域分析之类的。 比较经典的题目是 CF1870E Another MEX Problem,可以用剪枝…...

vue之Pinia
定义 Store | Pinia 开发文档 1.什么是Pinaia Pinia 是 Vue 的专属状态管理库,它允许你跨组件或页面共享状态。 2.理解Pinaia核心概念 定义Store 在深入研究核心概念之前,我们得知道 Store 是用 defineStore() 定义的,它的第一个参数要求是一…...
antd-vue 级联选择器默认值不生效解决方案
一、业务场景: 最近在使用Vue框架和antd-vue组件库的时候,发现在做编辑回显时** 级联选择器** 组件的默认值不生效。为了大家后面遇到和我一样的问题,给大家分享一下 二、bug信息: 三、问题原因: 确定不了唯一的值&a…...
分享53个Python源码源代码总有一个是你想要的
分享53个Python源码源代码总有一个是你想要的 链接:https://pan.baidu.com/s/1ew3w2_DXlSBrK7Mybx3Ttg?pwd8888 提取码:8888 项目名称 100-Python ControlXiaomiDevices DRF-ADMIN 后台管理系统 FishC-Python3小甲鱼 Flask框架的api项目脚手架 …...
【每日一题】658. 找到 K 个最接近的元素
658. 找到 K 个最接近的元素 - 力扣(LeetCode) 给定一个 排序好 的数组 arr ,两个整数 k 和 x ,从数组中找到最靠近 x(两数之差最小)的 k 个数。返回的结果必须要是按升序排好的。 整数 a 比整数 b 更接近 …...
)
并发任务队列(字节青训测试题)
需求描述 封装一个并发任务队列类,用于对一些异步任务按指定的并发数量进行并发执行。 /*** 延迟函数* param {number} time - 延迟时间* return {Promise} delayFn - 延迟函数(异步封装)*/ function timeout(time) {return new Promise((resolve) > {setTimeo…...
Ubuntu 安装Nacos
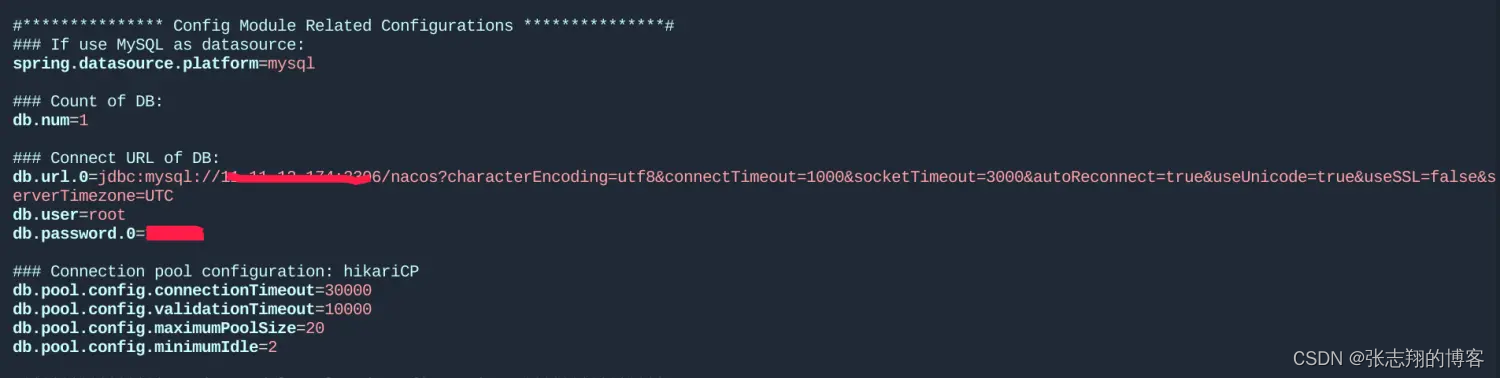
1、官网下载最新版nacos https://github.com/alibaba/nacos/releases 本人环境JDK8,Maven3.6.3,启动Nacos2.2.1启动失败,故切换到2.1.0启动成功 2、放到服务器目录下,我的在/home/xxx/apps下 3、解压 $ tar -zxvf nacos-serve…...

CSS 小球随着椭圆移动
html代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title><…...
【李沐深度学习笔记】线性代数
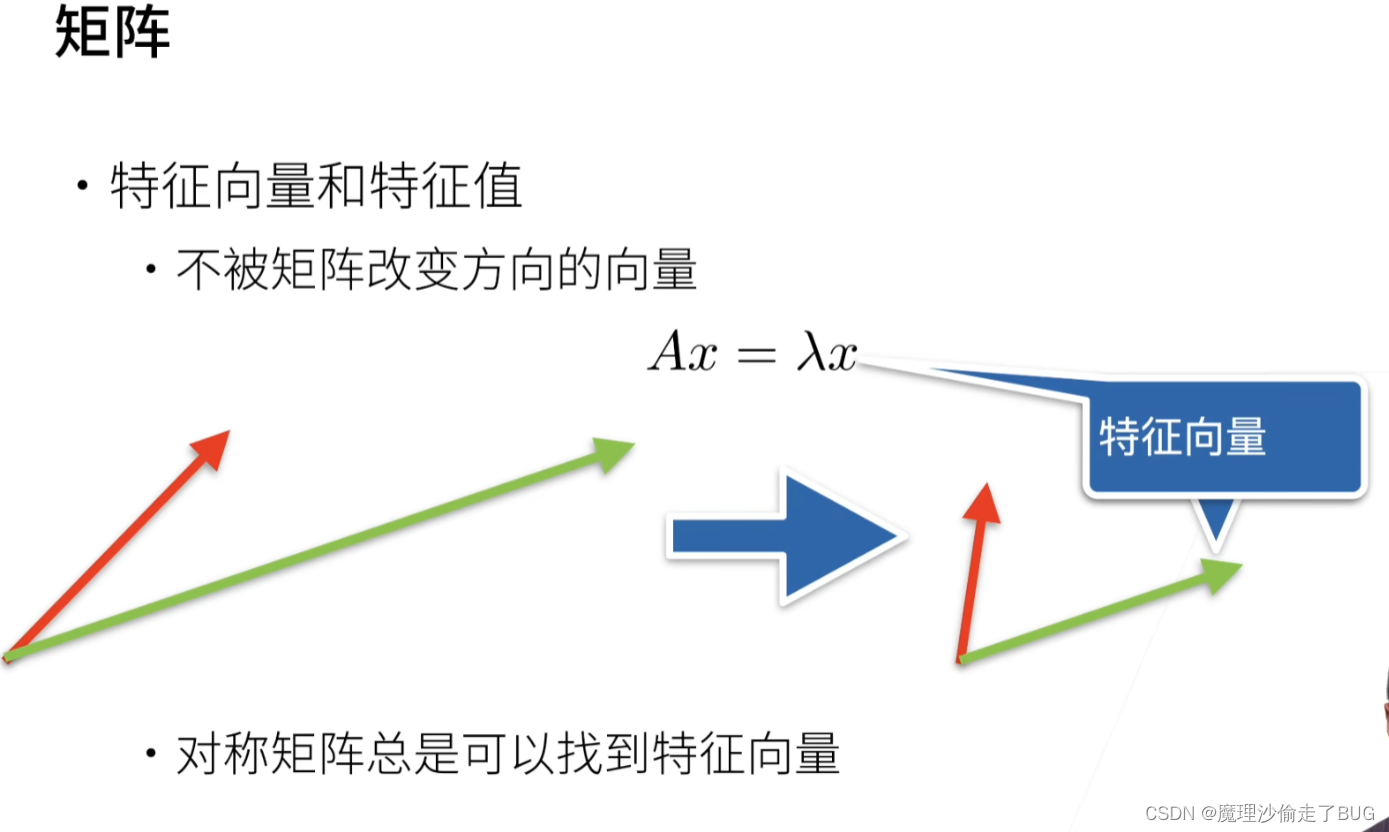
课程地址和说明 线性代数p1 本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。 线性代数 标量 标量(scalar),亦称“无向量”。有些物理量,只具有数值大小,…...

vuejs - - - - - 递归组件的实现
递归组件的实现 1. 需求描述:2. 效果图:3. 代码3.1 封装组件代码3.2 父组件使用 1. 需求描述: 点击添加行,增加一级目录结构当类型为object or array时,点击右侧➕,增加子集点击右侧🚮&#x…...

精准对接促合作:飞讯受邀参加市工信局举办的企业供需对接会
2023年9月21日,由惠州市工业和信息化局主办的惠州市工业软件企业与制造业企业供需对接会成功举办,对接会旨在促进本地工业软件企业与制造业企业的紧密合作,推动数字化转型的深入发展。此次会议在市工业和信息化局16楼会议室举行,会…...

数学建模之遗传算法
文章目录 前言遗传算法算法思想生物的表示初始种群的生成下一代种群的产生适应度函数轮盘赌交配变异混合产生新种群 停止迭代的条件遗传算法在01背包中的应用01背包问题介绍01背包的其它解法01背包的遗传算法解法生物的表示初始种群的生成下一代种群的产生适应度函数轮盘赌交配…...

ISO9001认证常见的不符合项
今天,整理了一些关于ISO9001质量管理体系审核最常见的不合格项,以供大家参考。 一、质量管理体系 1、质量手册(标准条款4.2.2) (1)各部门执行的文件与手册的规定不一致。 (2)质量…...
crypto:看我回旋踢
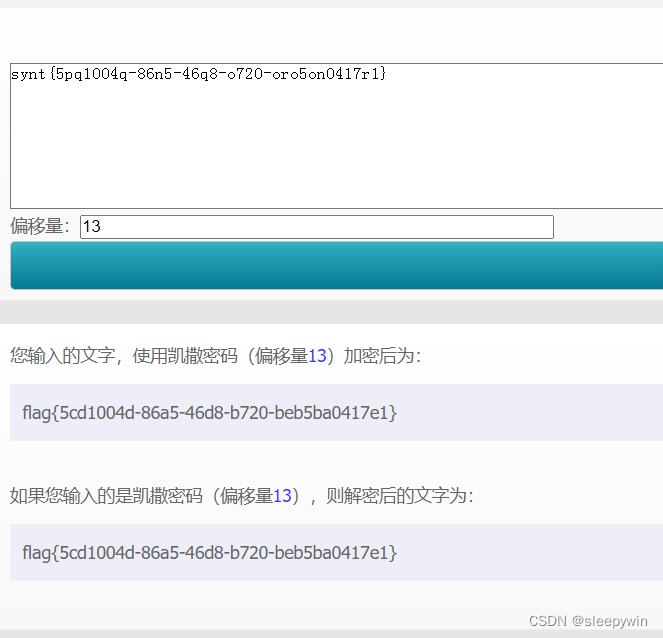
题目 下载压缩包后解压可得到提示文本 经过观察,synt{}这个提示与flag{}形式很像 由题目名中的回旋可以推测为凯撒密码,由凯撒密码的定义可知,需要先推出移位数,s->f数13次,因此移位数为13,解码可得...
Springcloud实战之自研分布式id生成器
一,背景 日常开发中,我们需要对系统中的各种数据使用 ID 唯一表示,比如用户 ID 对应且仅对应一个人,商品 ID 对应且仅对应一件商品,订单 ID 对应且仅对应 一个订单。我们现实生活中也有各种 ID ,比如身…...
java 企业工程管理系统软件源码 自主研发 工程行业适用
工程项目管理软件(工程项目管理系统)对建设工程项目管理组织建设、项目策划决策、规划设计、施工建设到竣工交付、总结评估、运维运营,全过程、全方位的对项目进行综合管理 工程项目各模块及其功能点清单 一、系统管理 1、数据字典&am…...

Spring Cloud Alibaba Nacos 2.2.3 (4) - 本地源码编译 调试
下载nacos nacos在GitHub上有下载地址:https://github.com/alibaba/nacos/releases,可以选择任意版本下载。 我下载的是2.2.3 版本 导入idea mvn 安装包 1,切换到Terminal ,并且使用command prompt模式 2,执行 mvn -Prelease…...

WKB近似
WKB方法用于研究一种特定类型的微分方程的全局性质 很有用这种特定的微分方程形如: 经过一些不是特别复杂的推导,我们可以得到他的WKB近似解。 该近似解的选择取决于函数和参数的性质同时,我们默认函数的定义域为当恒大于零,时: 当…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
