Denoising diffusion implicit models 阅读笔记
Denoising diffusion probabilistic models (DDPMs)从马尔科夫链中采样生成样本,需要迭代多次,速度较慢。Denoising diffusion implicit models (DDIMs)的提出是为了加速采样过程,减少迭代的次数,并且要求DDIM可以复用DDPM训练的网络。
加速采样的基本思路是,DDPM的生成过程需要从 [ T , ⋯ , 1 ] [T,\cdots,1] [T,⋯,1]的序列逐步采样,DDIM则可以从 [ T , ⋯ , 1 ] [T,\cdots,1] [T,⋯,1]的子序列采样来生成,通过跳步的方式减少采样的步数。
非马尔科夫的前向过程
DDPM中推理分布(inference distribution) q ( x 1 : T ∣ x 0 ) q(\mathbf x_{1:T}|\mathbf x_0) q(x1:T∣x0)是固定的马尔科夫链。DDIM的作者考虑构造新的推理分布,该推理过程和DDPM优化相同的目标,但能产生新的生成过程。

考虑一个推理分布族Q,由实向量 σ ∈ R ≥ 0 T \sigma \in \mathbb{R}^T_{\ge 0} σ∈R≥0T索引:
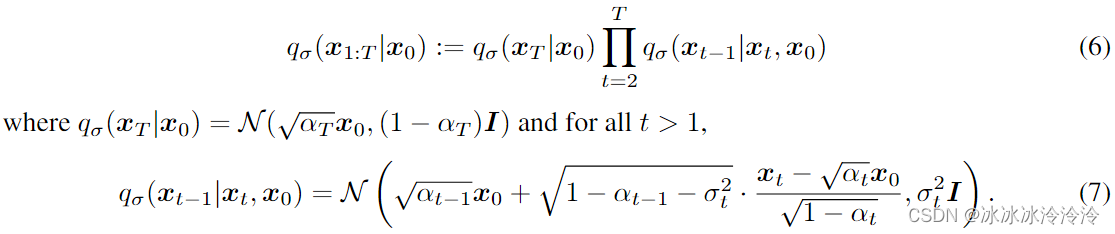
根据上面的定义有 q σ ( x t ∣ x 0 ) = N ( α t x 0 , ( 1 − α t ) I ) q_{\sigma}(\mathbf x_t | \mathbf x_0) = \mathcal{N}(\sqrt{\alpha_t}\mathbf x_0, (1-\alpha_t)I) qσ(xt∣x0)=N(αtx0,(1−αt)I)。
对应的前向过程也是高斯分布:
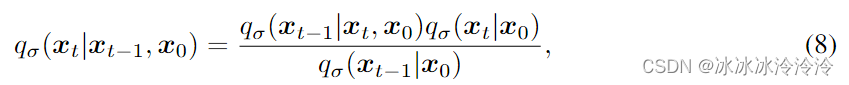
通过上面定义的推理过程,前向过程变成了非马尔科夫的,因为每一步都依赖 x 0 \mathbf x_0 x0。
参数 σ \sigma σ控制前向过程的随机性,如果 σ → 0 \sigma \rightarrow 0 σ→0,那么在已知 x 0 \mathbf x_0 x0和其中任一个 x t \mathbf x_t xt的情况下, x t − 1 \mathbf x_{t-1} xt−1是固定的。
根据上面的推理过程,定义需要学习的生成过程为:
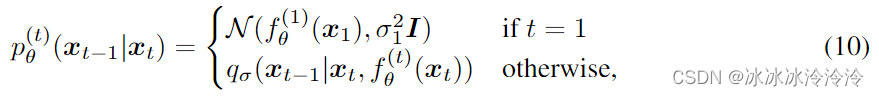
其中
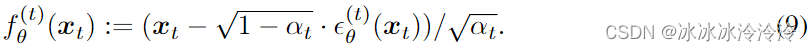
根据上面的定义的推理过程和生成过程,优化的目标是
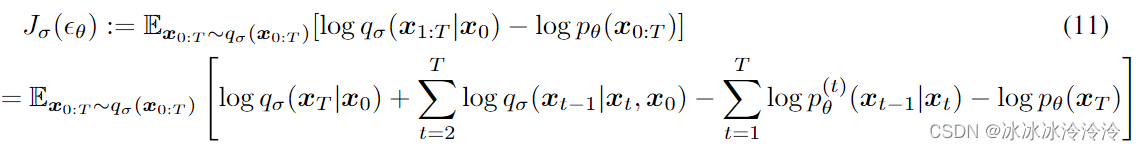
可以证明该优化目标和特定情况下DDPM的优化目标相同。
逆向生成过程的采样方法如下:
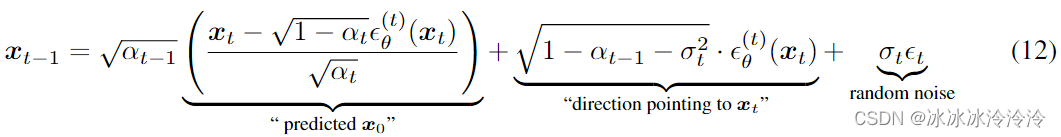
选择不同的 σ \sigma σ值会导致不同的生成过程,但它们使用相同的 ϵ θ \epsilon_{\theta} ϵθ模型。
如果 σ t = ( 1 − α t − 1 ) / ( 1 − α t ) ( 1 − α t ) / ( 1 − α t − 1 ) \sigma_t=\sqrt{(1-\alpha_{t-1})/(1-\alpha_{t})}\sqrt{(1-\alpha_{t})/(1-\alpha_{t-1})} σt=(1−αt−1)/(1−αt)(1−αt)/(1−αt−1),那么前向过程又变成了马尔科夫的,生成过程和DDPM一样。
如果 σ t = 0 \sigma_t=0 σt=0,那么随机噪声前的系数是0, x 0 \mathbf x_0 x0和 x T \mathbf x_T xT之间的关系是固定的,这属于隐概率模型(implicit probabilistic model)。因此,作者把这种情况称为denoising diffusion implicit model (DDIM)。
加速
为了加速采样,作者考虑下面的推理过程:
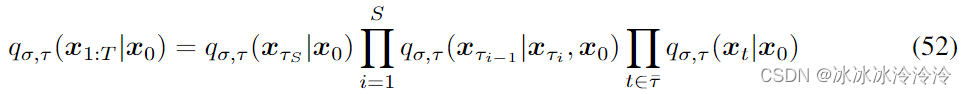
其中 τ \tau τ是长度为S的 [ 1 , ⋯ , T ] [1,\cdots,T] [1,⋯,T]的子序列, τ S = T \tau_S=T τS=T, τ ‾ : = { 1 , … , T } \ τ \overline{\tau}:=\{1,\ldots,T \} \backslash \tau τ:={1,…,T}\τ是除去子序列剩下的序号。
定义
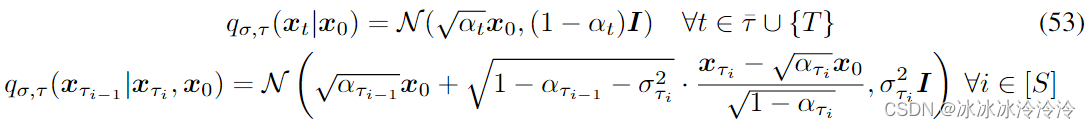 该推理分布对应的生成过程如下:
该推理分布对应的生成过程如下:
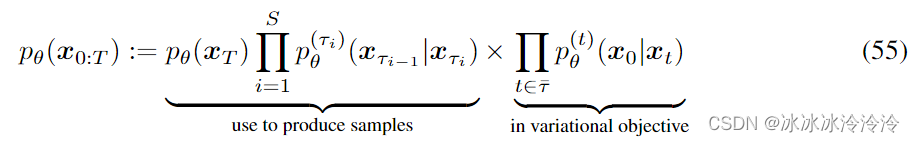
定义需要学习的概率为:
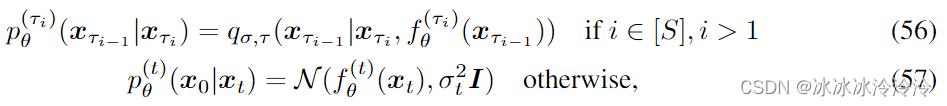
根据上面的定义的推理过程和生成过程,优化的目标是
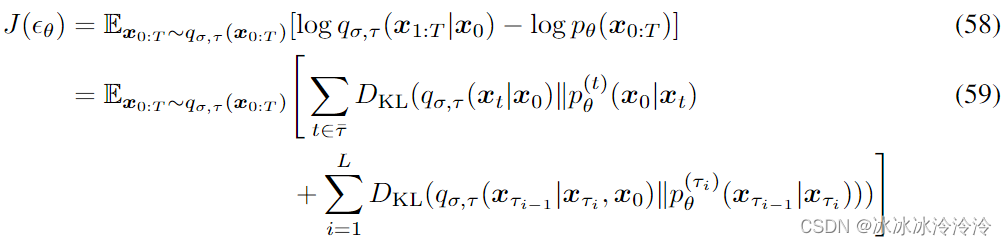
可以证明该优化目标和特定情况下DDPM的优化目标相同。
因此,可以利用DDPM训练的网络,但是从子序列采样生成图像。
相关文章:
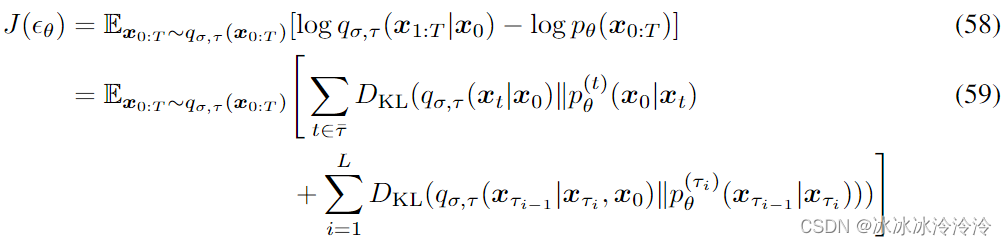
Denoising diffusion implicit models 阅读笔记
Denoising diffusion probabilistic models (DDPMs)从马尔科夫链中采样生成样本,需要迭代多次,速度较慢。Denoising diffusion implicit models (DDIMs)的提出是为了加速采样过程,减少迭代的次数,并且要求DDIM可以复用DDPM训练的网…...

【Java 基础篇】Executors工厂类详解
在多线程编程中,线程池是一项重要的工具,它可以有效地管理和控制线程的生命周期,提高程序的性能和可维护性。Java提供了java.util.concurrent包来支持线程池的创建和管理,而Executors工厂类是其中的一部分,它提供了一些…...

SpringBoot MongoDB操作封装
1.引入Jar包 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-mongodb</artifactId></dependency> 2.MongoDbHelper操作 /*** MongoDB Operation class* author Mr.Li* date 2022-12-05*…...

PyTorch 模型性能分析和优化 — 第 1 部分
一、说明 这篇文章的重点将是GPU上的PyTorch培训。更具体地说,我们将专注于 PyTorch 的内置性能分析器 PyTorch Profiler,以及查看其结果的方法之一,即 PyTorch Profiler TensorBoard 插件。 二、深度框架 训练深度学习模型,尤其是…...

Unity3D 简易音频管理器
依赖于Addressable 依赖于单例模板:传送门 using System.Collections.Generic; using System.Security.Cryptography; using System; using UnityEngine; using UnityEngine.AddressableAssets;namespace EasyAVG {public class AudioManager : MonoSingleton<…...

【李沐深度学习笔记】线性回归
课程地址和说明 线性回归p1 本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。 线性回归 如何在美国买房(经典买房预测问题) 一个简化的模型 线性模型 其中, x → [ x 1 , x 2 ,…...
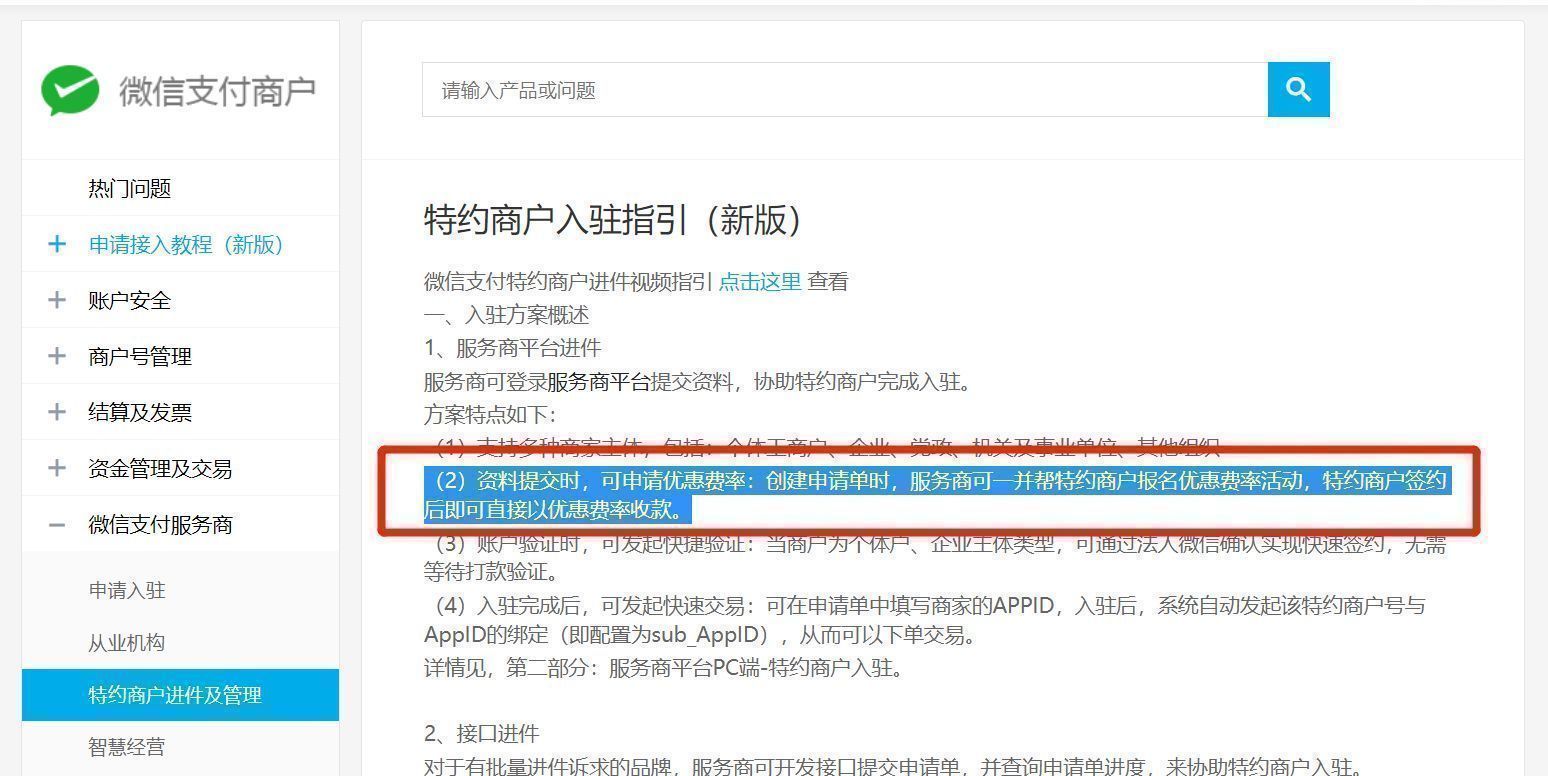
微信收款码费率0.38太坑了
作为一个有多年运营经验的商家,我本人在申请收款功能时曾经走过了不少弯路。我找遍了市面上的知名的支付公司,但了解到的收款手续费率通常都在0.6左右,最低也只能降到0.38。这个过程吃过不少苦头。毕竟,收款功能是我们商家的命脉&…...

【学习笔记】CF1103D Professional layer
首先分析不出啥性质,所以肯定是暴力优化😅 常见的暴力优化手段有均摊,剪枝,数据范围分治(points),答案值域分析之类的。 比较经典的题目是 CF1870E Another MEX Problem,可以用剪枝…...

vue之Pinia
定义 Store | Pinia 开发文档 1.什么是Pinaia Pinia 是 Vue 的专属状态管理库,它允许你跨组件或页面共享状态。 2.理解Pinaia核心概念 定义Store 在深入研究核心概念之前,我们得知道 Store 是用 defineStore() 定义的,它的第一个参数要求是一…...
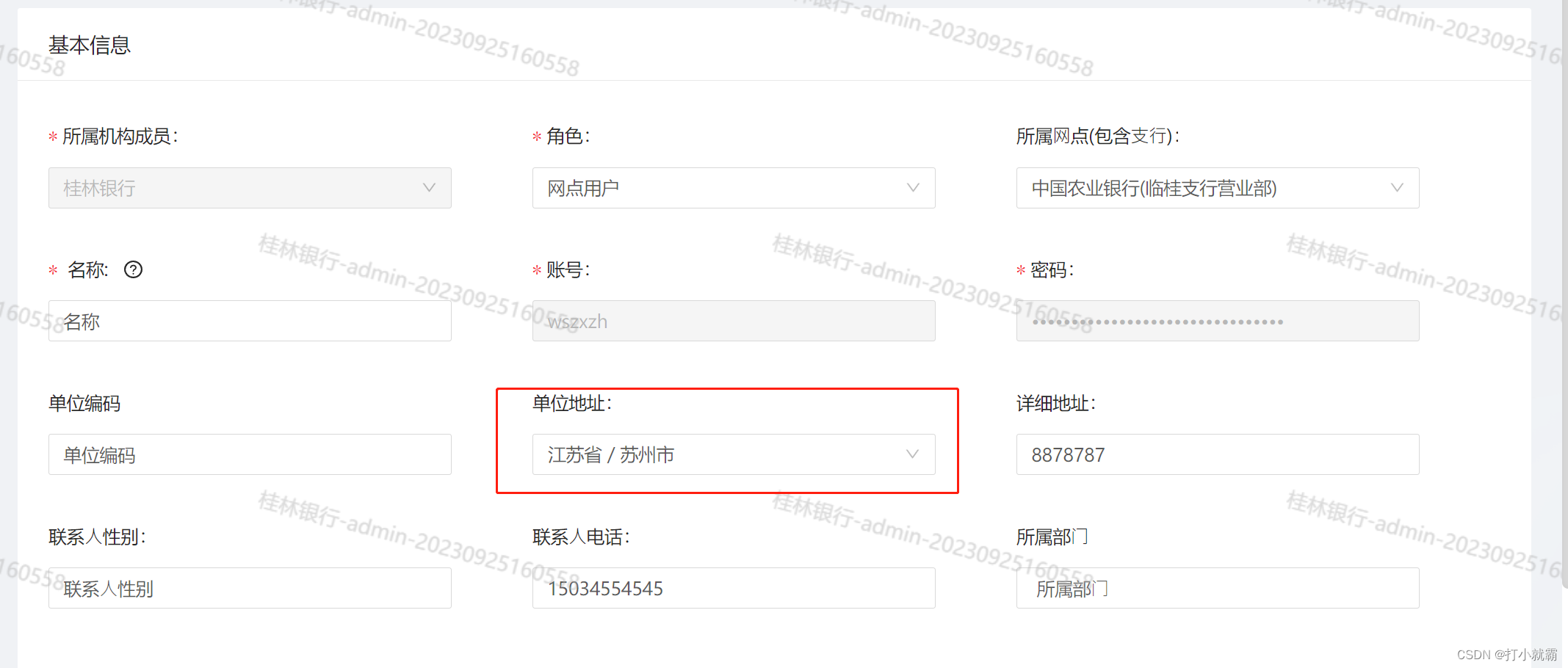
antd-vue 级联选择器默认值不生效解决方案
一、业务场景: 最近在使用Vue框架和antd-vue组件库的时候,发现在做编辑回显时** 级联选择器** 组件的默认值不生效。为了大家后面遇到和我一样的问题,给大家分享一下 二、bug信息: 三、问题原因: 确定不了唯一的值&a…...
分享53个Python源码源代码总有一个是你想要的
分享53个Python源码源代码总有一个是你想要的 链接:https://pan.baidu.com/s/1ew3w2_DXlSBrK7Mybx3Ttg?pwd8888 提取码:8888 项目名称 100-Python ControlXiaomiDevices DRF-ADMIN 后台管理系统 FishC-Python3小甲鱼 Flask框架的api项目脚手架 …...
【每日一题】658. 找到 K 个最接近的元素
658. 找到 K 个最接近的元素 - 力扣(LeetCode) 给定一个 排序好 的数组 arr ,两个整数 k 和 x ,从数组中找到最靠近 x(两数之差最小)的 k 个数。返回的结果必须要是按升序排好的。 整数 a 比整数 b 更接近 …...
)
并发任务队列(字节青训测试题)
需求描述 封装一个并发任务队列类,用于对一些异步任务按指定的并发数量进行并发执行。 /*** 延迟函数* param {number} time - 延迟时间* return {Promise} delayFn - 延迟函数(异步封装)*/ function timeout(time) {return new Promise((resolve) > {setTimeo…...
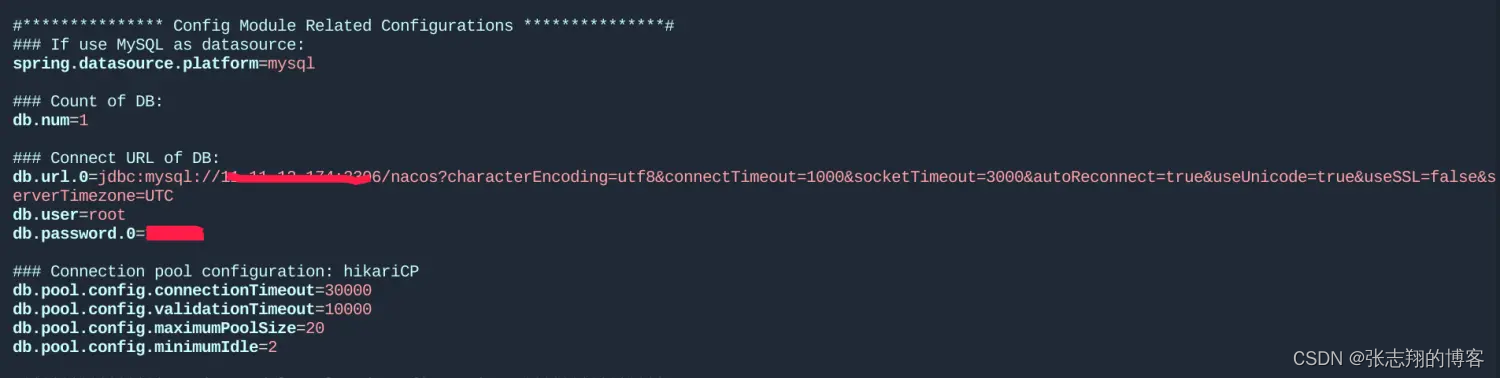
Ubuntu 安装Nacos
1、官网下载最新版nacos https://github.com/alibaba/nacos/releases 本人环境JDK8,Maven3.6.3,启动Nacos2.2.1启动失败,故切换到2.1.0启动成功 2、放到服务器目录下,我的在/home/xxx/apps下 3、解压 $ tar -zxvf nacos-serve…...

CSS 小球随着椭圆移动
html代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title><…...
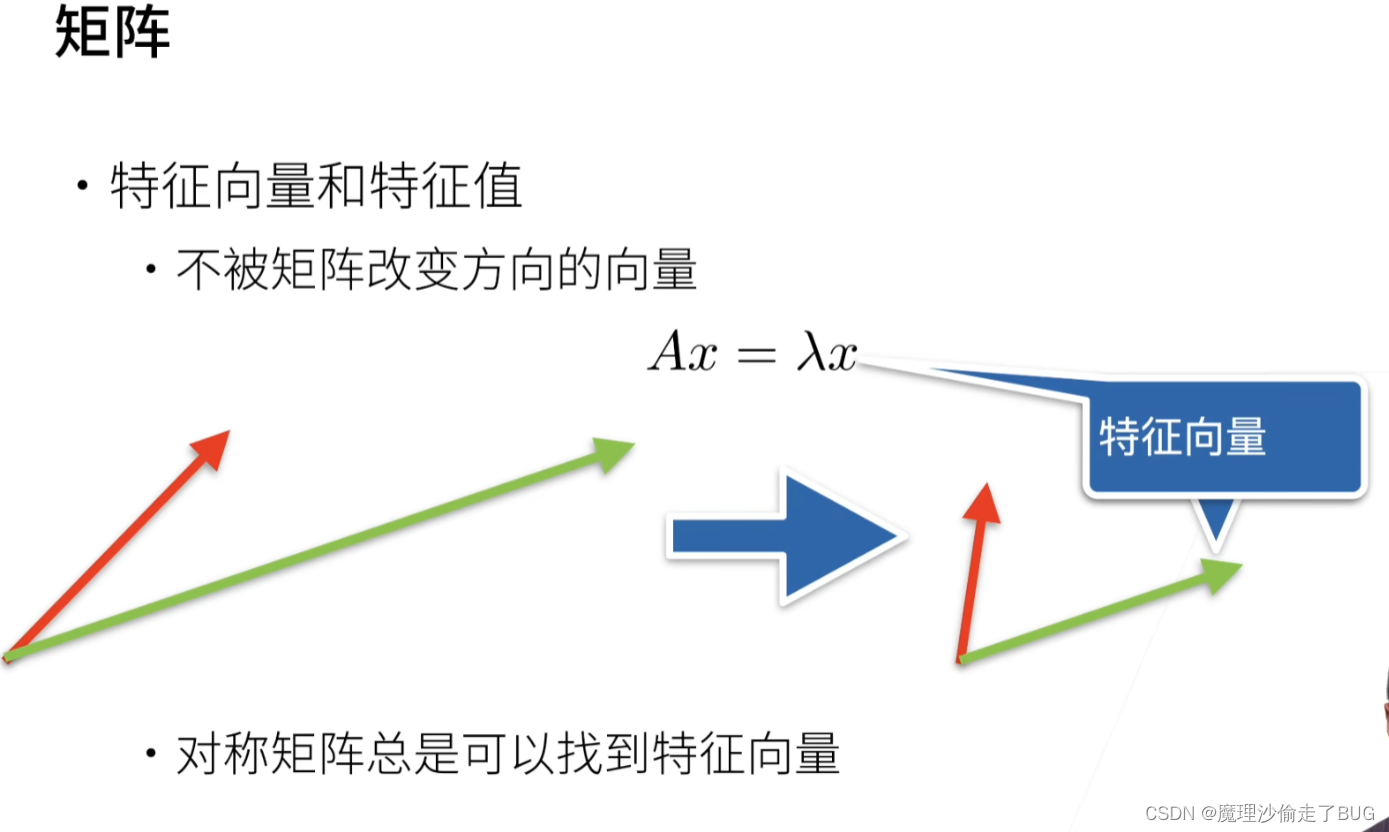
【李沐深度学习笔记】线性代数
课程地址和说明 线性代数p1 本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。 线性代数 标量 标量(scalar),亦称“无向量”。有些物理量,只具有数值大小,…...

vuejs - - - - - 递归组件的实现
递归组件的实现 1. 需求描述:2. 效果图:3. 代码3.1 封装组件代码3.2 父组件使用 1. 需求描述: 点击添加行,增加一级目录结构当类型为object or array时,点击右侧➕,增加子集点击右侧🚮&#x…...

精准对接促合作:飞讯受邀参加市工信局举办的企业供需对接会
2023年9月21日,由惠州市工业和信息化局主办的惠州市工业软件企业与制造业企业供需对接会成功举办,对接会旨在促进本地工业软件企业与制造业企业的紧密合作,推动数字化转型的深入发展。此次会议在市工业和信息化局16楼会议室举行,会…...

数学建模之遗传算法
文章目录 前言遗传算法算法思想生物的表示初始种群的生成下一代种群的产生适应度函数轮盘赌交配变异混合产生新种群 停止迭代的条件遗传算法在01背包中的应用01背包问题介绍01背包的其它解法01背包的遗传算法解法生物的表示初始种群的生成下一代种群的产生适应度函数轮盘赌交配…...

ISO9001认证常见的不符合项
今天,整理了一些关于ISO9001质量管理体系审核最常见的不合格项,以供大家参考。 一、质量管理体系 1、质量手册(标准条款4.2.2) (1)各部门执行的文件与手册的规定不一致。 (2)质量…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...
