描述性统计分析
前言:
本专栏参考教材为《SPSS22.0从入门到精通》,由于软件版本原因,部分内容有所改变,为适应软件版本的变化,特此创作此专栏便于大家学习。本专栏使用软件为:SPSS25.0
本专栏所有的数据文件可在个人主页—我的资源中获取哦!
1.描述性统计分析
描述性统计分析是一种通过统计指标和图表对数据进行总结、描述和解释的方法。它主要用于对数据集的特征进行量化和可视化,以便更好地理解数据。
常见的描述性统计指标包括:
- 中心趋势度量:例如平均值(均值)、中位数和众数,用于表示数据的集中程度。
- 离散程度度量:例如标准差、方差和极差,用于表示数据的分散程度。
- 偏态和峰度:用于描述数据分布的对称性和尖峰性。
- 百分位数:用于表示数据的相对位置和排序。
除了以上指标,描述性统计分析还可以通过绘制图表来可视化数据分布和趋势。常见的图表包括直方图、箱线图、散点图和饼图等。
2.描述性统计分析的SPSS实现
2.1 打开数据文件data4-2,选择“分析”——“描述性统计”——“描述”,弹出如下对话框。

2.2 选中左侧“身高”变量,将其移到右边变量框中,并勾选“将标准化得分另存为变量”复选框。
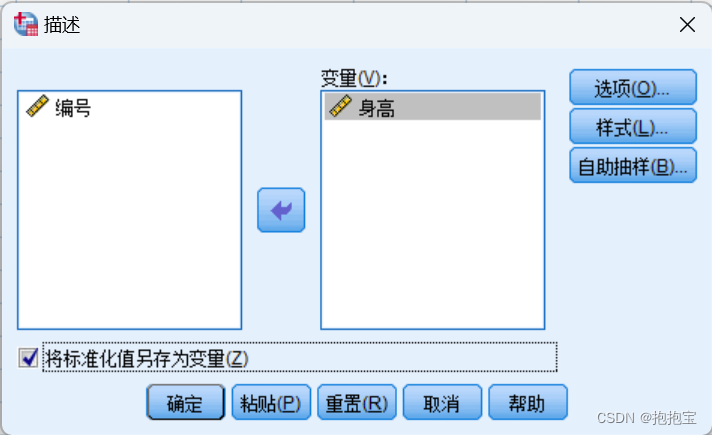
2.3 单击 “选项”按钮,弹出“描述:选项”对话框,按照下图勾选对应选项,然后单击继续。

2.4 完成所有设置后 ,单击确定得出分析结果。
3.描述性统计分析结果
下图显示出来描述性统计分析的各项指标结果:

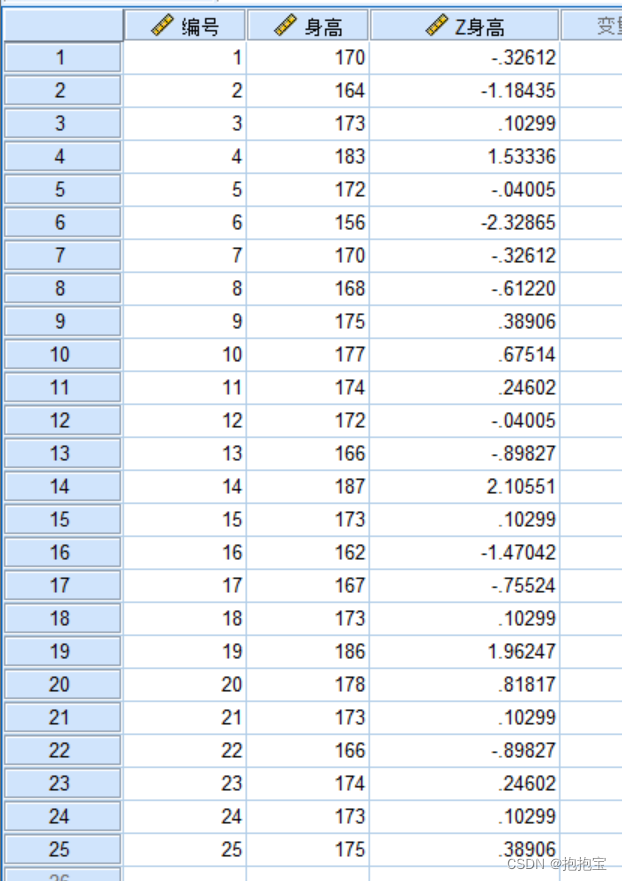
可以根据上表的数据进行分析。此外,描述性统计分析还可以把原始变量数据转化成标准化的变量在数据窗口呈现,如下图所示:
相关文章:

描述性统计分析
前言: 本专栏参考教材为《SPSS22.0从入门到精通》,由于软件版本原因,部分内容有所改变,为适应软件版本的变化,特此创作此专栏便于大家学习。本专栏使用软件为:SPSS25.0 本专栏所有的数据文件可在个人主页—…...

Visual Studio2019 C++ 编程问题集锦
“const char*” 类型的值不能用于初始化“char*"类型的实体 解决方案一: 点击项目->属性->C/C>语言->符合模式,将原来的“是”改为“否”即可。解决方案二: 在声明变量 char* 时改成 const char *即可...
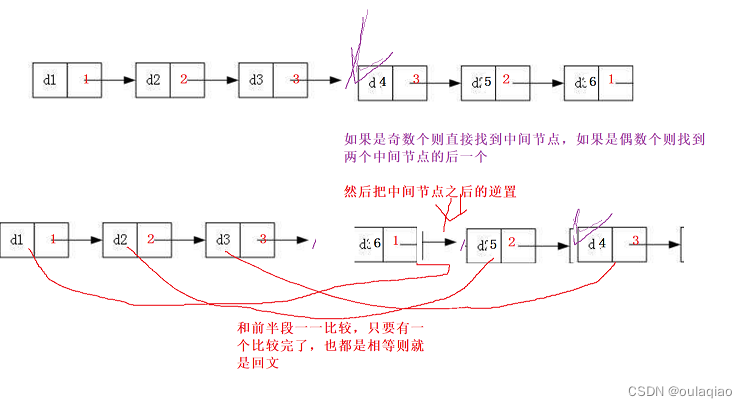
链表的回文判断
思路: 找中间节点–>逆置->比较 代码: /*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/struct ListNode* middleNode(struct ListNode* head) { struct ListNode*slowhead; struct ListNode*f…...

281_JSON_两段例子的比较,哪一段更简洁、易懂、没有那么多嵌套
《第一份:》//组装Notificationif (bSendAINotification){BOOST_AUTO(iter_flashnotification, documentAll.FindMember("Notification"));if (iter_flashnotification != documentAll....

想要精通算法和SQL的成长之路 - 最长递增子序列 II(线段树的运用)
想要精通算法和SQL的成长之路 - 最长递增子序列 II(线段树的运用) 前言一. 最长递增子序列 II1.1 向下递推1.2 向上递推1.3 更新操作1.4 查询操作1.5 完整代码: 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 最长递增子序列 II 原题链接…...

java用easyexcel按模版导出
首先在项目的resources下面建一个template包,之后在下面创建一个模版,模版格式如下: 名称为 financeReportBillStandardTemplateExcel.xlsx: {.fee}类型的属性值,是下面实体类的属性,要注意这里面的格式&a…...
Servlet执行流程生命周期方法介绍体系结构、Request和Response的功能详解
🐌个人主页: 🐌 叶落闲庭 💨我的专栏:💨 c语言 数据结构 javaEE 操作系统 Redis 石可破也,而不可夺坚;丹可磨也,而不可夺赤。 Servlet 一、 Servlet执行流程二、Servlet生…...
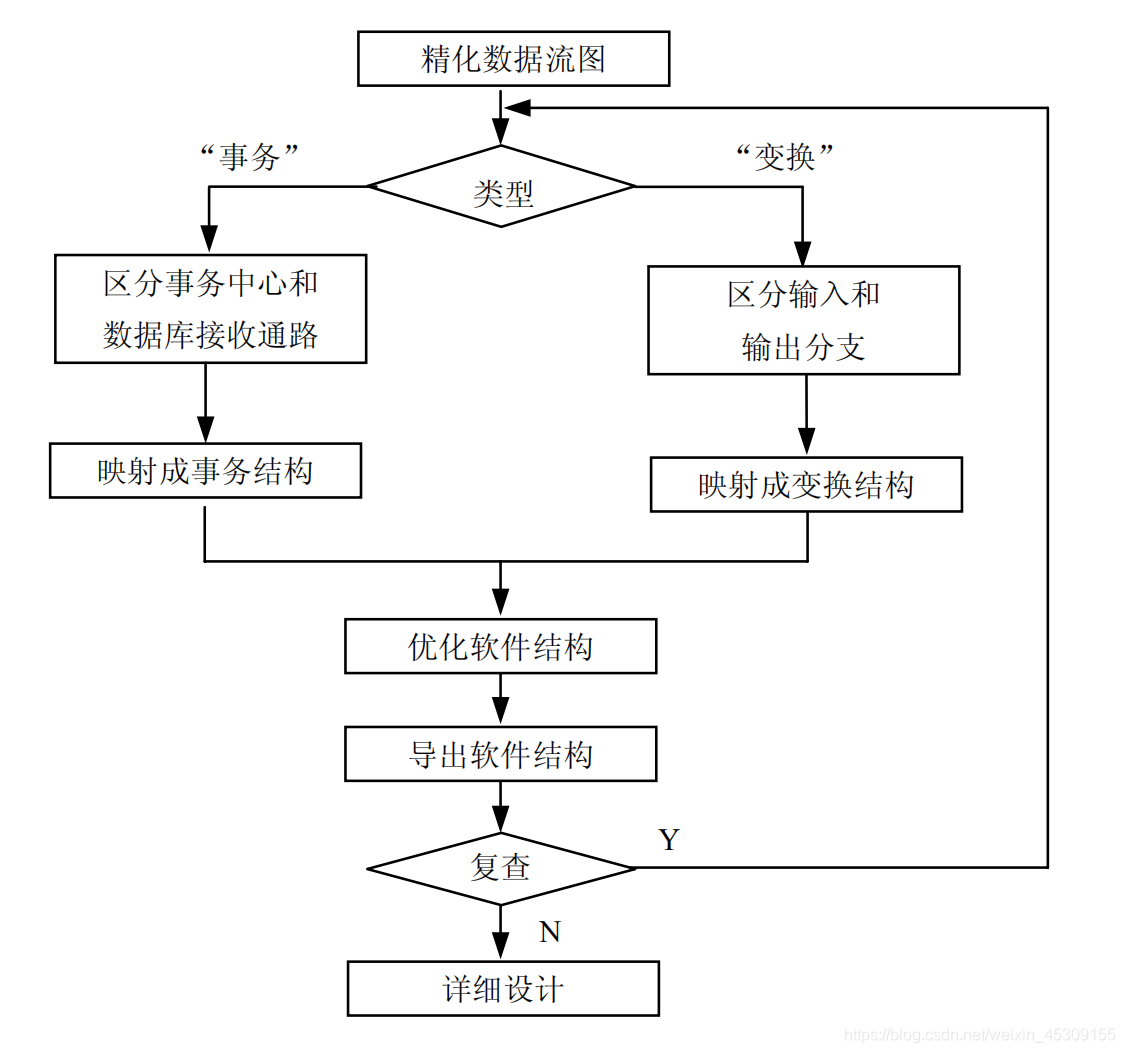
软件工程之总体设计
总体设计是软件工程中的一个重要阶段,它关注整个系统的结构和组织,旨在将系统需求转化为可执行的软件解决方案。总体设计决定了系统的架构、模块划分、功能组织以及数据流和控制流等关键方面。 可行性研究 具体方面:经济可行性、技术可行性…...

监控员工电脑文件拷贝记录:电脑怎么看员工复制文件的历史记录
在现代企业管理中,数据安全和保密是极其重要的一环。企业需要确保敏感信息不被泄露,以防止可能的法律纠纷和经济损失。为此,许多公司都采取了一些措施来监控员工的电脑使用行为。其中,监控文件拷贝记录是一种常见的方法。本文将详…...
文件通用下载方法封装)
vue中request.js中axios请求和(若依)文件通用下载方法封装
vue中request.js中axios请求和(若依)文件通用下载方法封装 1.request.js import axios from axios import { Message, Loading } from element-ui import { saveAs } from file-saver // 创建axios实例 const request axios.create({// 这里可以放一…...
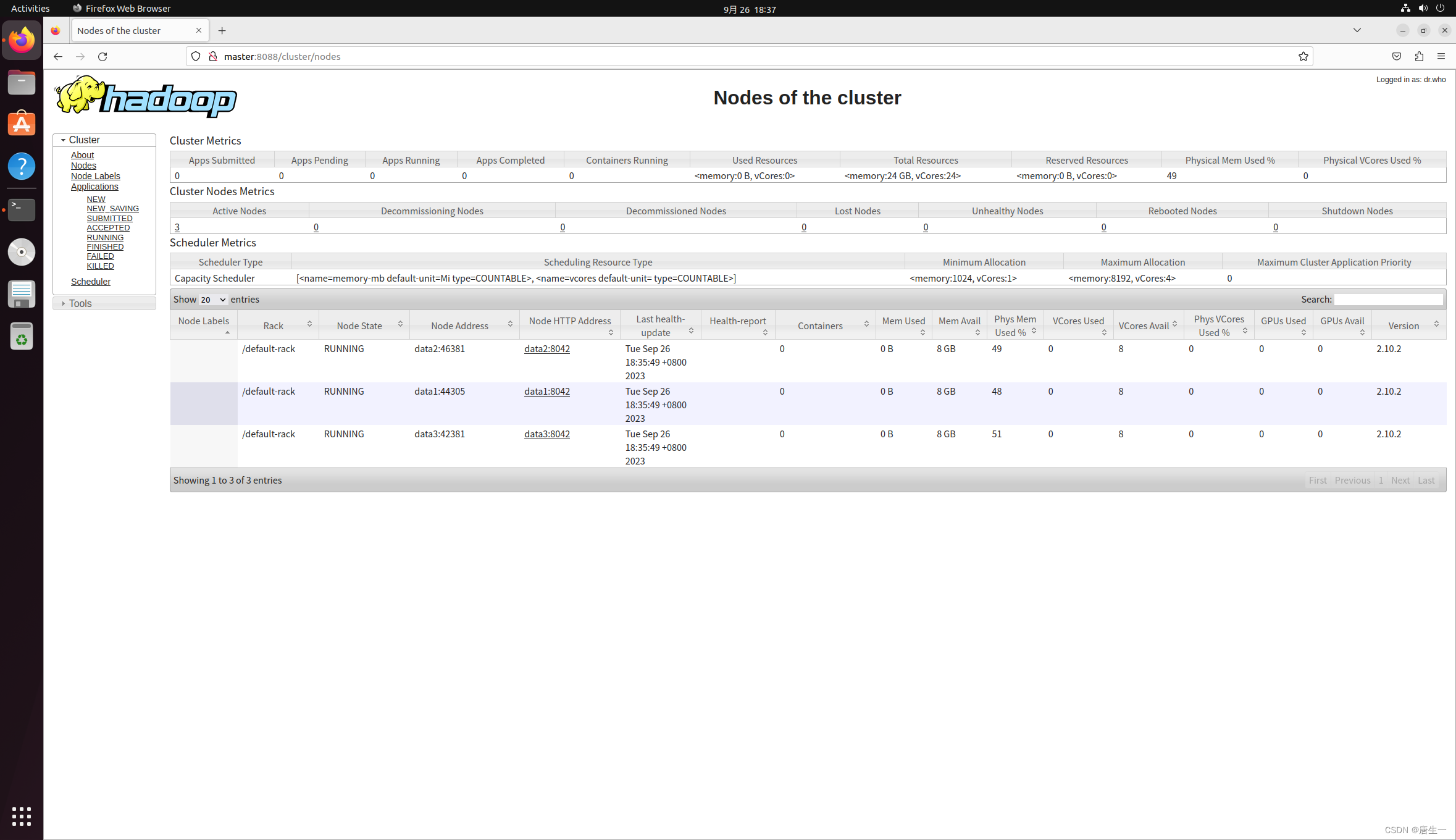
【大数据存储与处理】1. hadoop单机伪分布安装和集群安装
0. 写在前面 0.1 软件版本 hadoop2.10.2 ubuntu20.04 openjdk-8-jdk 0.2 hadoop介绍 Hadoop是一个由Apache基金会所开发的分布式系统基础架构。用户可以在不了解分布式底层细节的情况下,开发分布式程序。充分利用集群的威力进行高速运算和存储。Hadoop实现了一个…...

linux通过time命令统计代码编译时间
首先编写一个编译脚本 build.sh 内容如下: 然后执行time sh build.sh 编译完成后输出三个时间 time sh xxx.sh # 会返回3个时间数据 (1) real:从进程 ls 开始执行到完成所耗费的 CPU 总时间。该时间包括 ls 进程执行时实际使用的 CPU 时间,…...

logback日志是怎么保证多线程输出日志线程安全的
logback中的单例模式 logback日志框架使用了单例设计模式来进行日志输出。在logback中,Logger类是一个关键的组件,它负责记录和输出日志消息。 Logger类使用了单例设计模式,确保在一个应用程序中只存在一个Logger实例。这样做的好处是可以确…...

2022年统计用区划代码表SQL 01
行政区划代码为国家公布的六位县级以上行政区划代码 行政区编码的用途: APP里做城市级联选择根据身份证前六位获取用户所在城市区县 370786 昌邑市 370800 济宁市 370811 任城区 370812 兖州区 百度高德等接口通常都会返回adcode字段 (行政区编码)根据 行政区编…...

EM@基本初等函数@幂和根式@指数函数
abstract 基本初等函数幂和根式指数函数 指数和幂 正整指数幂 a n a^{n} an a ⋯ a ⏟ n 个 \underbrace{a\cdots{a}}_{n个} n个 a⋯a, n ∈ N n\in\mathbb{N^{}} n∈N 其中 a n a^{n} an称为** a a a的 n n n次幂** a a a叫做幂的底数, n n n叫做幂的指数 正整指数…...

时序预测 | MATLAB实现NGO-GRU北方苍鹰算法优化门控循环单元时间序列预测
时序预测 | MATLAB实现NGO-GRU北方苍鹰算法优化门控循环单元时间序列预测 目录 时序预测 | MATLAB实现NGO-GRU北方苍鹰算法优化门控循环单元时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 MATLAB实现NGO-GRU北方苍鹰算法优化门控循环单元时间序列预测&#…...

element 二次确认框,内容自定义处理
上代码: async inspectionTypeOff(row) {console.log(row.id);let taskArray await this.getTaskList(row.id); // 查询关联的任务console.log("taskArray", taskArray);let messageTip taskArray.length > 0? <div><p>确认禁用巡检项&…...

【软件设计师-中级——刷题记录4(纯干货)】
目录 进度管理工具Grantt图:程序语言基础:高级语言源程序模式: 每日一言:持续更新中... 个人昵称:lxw-pro 个人主页:欢迎关注 我的主页 个人感悟: “失败乃成功之母”,这是不变的道理…...

9.24 校招 实习 内推 面经
绿泡*泡: neituijunsir 交流裙 ,内推/实习/校招汇总表 1、自动驾驶一周资讯 - 小马智行在京开展“车内无人”出行服务商业化试点,余承东将升任车BU董事长 自动驾驶一周资讯 - 小马智行在京开展“车内无人”出行服务商业化试点࿰…...
持续更新)
第二章:25+ Python 数据操作教程(第二十五节用 PYTHON 和 R 制作祝福圣诞节)持续更新
这篇文章献给所有 Python 和 R 编程爱好者...通过以下程序在同行中炫耀您的知识。作为一名数据科学专业人士,您希望自己的愿望在圣诞节前夕变得特别。如果您观察代码,您还可以学到 1-2 个技巧,您可以在以后的日常任务中使用这些技巧。 方法 1:运行以下程序,看看我的意思 R…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
