2022 赣育杯 CTF --- Crypto Lost_N wp
文章目录
- 前言
- 题目
- 解题过程
- 解题代码
前言
这是去年江西省赛一道有点小坑的密码题,当时没做出来,今天回想起来重新做一下并且记录一下。
题目
Lost_N.py
import gmpy2
from Crypto.Util.number import *
# part1
flag = b'SangFor{}'
d = getPrime(435)
count = 5
while count > 0:p = getPrime(512)q = getPrime(512)n = p * qphi = (p-1) * (q-1)e = gmpy2.invert(d, phi)print('c =', pow(bytes_to_long(flag), e, n))print('n =', n)print('e =', e)count -= 1# part2
p = getPrime(1024)
q = getPrime(1024)
n = p * q
e = 0x10001
s = pow(900*p - 218*q, n-p-q, n)c = pow(last_n, e, n)
print('n =', n)
print('c =', c)
print('s =', s)output.txt
c = 13007070082982086015048648249698272815655157209727275797297990841215796701955079738986996208838342773211678208282162295881823413924960399315068498509939876883297864092435101096694113071462267388158595518905101264654742860199638059278239359756219217345342001728599121265614144789005805619626458575126846199823
n = 145575036089862184772968012014750816659166028840828357885024516131565102712346345625910708214596157522939248398359985832422106056149116726640753670919394145037581595172384392223713667048639158944450925280598688178812170253438103664700756173806183649477673497327790421063029596049211220930285435947389700047717
e = 6104905725583061487097813130111812725712623687061285535333592835899028572315489283518324105546236465450024687400996793197533588656449965379858202658832799573292015786259804984314040621630959455897094519928941186899832366216111359619637121411868069759469878142871432060850651758192209783752650530390826992241
c = 59089700172263364510471541430195724136973801897202789650586019199451669728729101831161257990233999290546484165767660146638244043033774379664984894178111808280076960669616271416462197675878517863817855762681885790347812435849975072020273928469523961698304409181769820692602979823921421820511589311465948726144
n = 171055961405321566289532118753767563629109197214150143506779656820887080836894368955104877312070939117885512468517951216152955714212079279910802095156350517032659766690101321767892798466184405283403136505441356956934759143173462058806620784497304916652269667097971495139608875846338091109621496242787157524093
e = 30639328953696065722075015079387560065304228779854040351182305267894609577068955234152835797506237100956072519388029280776532681675227753068574540049244778077615881093270476533536257809592871380358708151151683035275615961208943826349952952069226829397420921321531951316523368786223865432179572145636266109841
c = 24257648301491609274972482189063774024772127961295257418254600487615473027418329077996964279110710299066082437371516700591657843057597234861450272363240630164504734590903528165056021531272324846249133757036680429476939369309982196345252669711604534774523215422683385359295249160897422071732828044179085194829
n = 99735998821682404719682435155046621256882035421263371444758755082217342389922499214602126376005623406797486880520535486455942687180959663032781490782870080236095770591995437146834606144553095293546973559144743704707021952152013362323293717685161426469215016058837362232410103330238322051089471439573994907641
e = 81580834845272005549352820344384188734735397414102222005750919291263464191246301214086773744759605577533897859454210564034313392997143493147211816886655474145064723790935089304983994174659126346174766206623180477360887938029897557683160392738708450965784921553806400996559956745732829531154835363767773681061
c = 105310270039347542993580213074911114373638987155564864341577443142664062749969114572669295115218200093381519732560445712425129105002834596010587656544575627162469582470245756143405705971157024449801127133755773536097173259762599166367688198314997549663330392481942723997656023552049910279885657664434799986156
n = 118810172988175650374012494943583618875926370822995080847518376655089884052560062524542984436965153851285471302754389325839857100631601002627184437173686224779115595776898914116490948408328080895524604124937295381872443370706017215743101755848741173976351916104362193751372512936063892260855907424754174906407
e = 57970672598245590037421993575987847127437841761387257183798066822318596392918179916711068560675528926294272336883938499809087281773070750919594701600347605662910664129043903749270935721912605279738208730075557097647316659218872977257614306133047318781156168440924237849014715453590776000659069078250493480521
c = 50430341205487530895874157969557709374947862873979946417751686643857339147558892228311050765271667685452170747716439387141655285820549605442067496018168606163031122498272292974227360674531814593351170403519198099247839499352696883293133549658442172721339510734646474794377043195182186423251146266787514560008
n = 80837118813383038376595037732171926303253457956240963765871280771175535050976501573174357090322706934194338649978803681581485022992041019276854467388155755920855237665754031077890133388056350355753218650482718197635332681450734918373003830855184694566883308495322647552169761087814135330222306083205629967447
e = 51172856769626923894369204019063376718507295306271724506808987836327051371415876890252665691760404489737902233106400428873399230724307065583727090788789453353097657968301923726049631007431604461521879288667433292135840271678776989737261214286587609316530839676362375173635542358540766454865624476392874630929
c = 24533435736573623334539431528997922833496063510219641412038735658846891237553927656156039267456590702682308774830590768888594750053426705504840854071081487058180327084899496154314864910274839867793265086899109787190447838634454294468362549369144295591261617705578124672391399319219038350878856530074063011081?
?
?
?
?e = 71905546659735491498365580186225996341462093571074706903142472266442052559638067842283521897292088493599089076218507596455101425837547743511983105386966540811629138324774640350969049873787070380161376295760563611617178869788237730560614549740931199083194226891873779907795120035746039593933256380499568775673n = 20955464633057600258987829727550073699845816289000240676927869818926752810905511184835302717855745473943671910742784074561535017974853574714483642916831791020944940633062963043482236587316552330558006573820423830770910893877191630012247591380869307656539553888318621170921800017818132160253923739647771452839191101104391894609403591447166963426444018303147924843072923713248135717578047687411974516038299879758561542241544862102935741869647633013298181782208467117482306148238724598730801037692668154263059348953587766571379262442743822007387408949824805991797355089583176028081305319076896384126383926193964322235633
c = 14815997295683082265558346455845370590765145583224067337292601455640475216349267044144296003388877395546880235511728120803143112914764263292087421926972160283428440959367872665892349776616002018624301524264223581314248857537034849571849747613963209414193510408342387107662655487869098045345428379025731617851483935711671021438908270746316921057871871545763798735895118697635903815383424855759281301248295597297869474539060531099443223045844791615425429748703429968627505406271675074549912664863784774239200764403372298995457799473112713379340870305136776932539188516395526955161359417473843082895317392495109895085666
s = 14728527428626630951705148488338433865446345521255631461200851513782412494843597938863837697938230856843797646287742397249258609197032095158567448934855031190354034543862057663422053672290704598313096289223478302733688501373756860855445632789922930577582465209872782549135254792729915747104521949095814028476908208917363509089190935273004331739978623136706041729628143765893264698948654175039064609891374587695812144855411176143224066975193255513405865992328257766815240718115442741846443490733767716842367336385132648983241895710001620533668392060358573295789752856876282590472528110546264872047138094995909454134250解题过程
拿到题目,d = getPrime(435),一眼丁真就发现是共私钥指数攻击,利用5组n,e构造一个格子,解出d
d = 702892213537584353870078517457565977170149896982141355183314129206210172057118726177119088005142585861765983210442568598043826
接下来不就是简简单单的RSA解密咯,flag手到擒来。
带入进去一计算得到的m是一堆乱码?
坏!!!遭骗,遭阳之大骗。
重新计算了一下d的长度:419bit,不是题目给的435bit
仔细看了一下题目代码以及output,output中有6组c和e并且最后一组的c与e之间缺少了n,我猜出题人应该是循环生成了6组数据,然后将第6组的n作为part2部分的m,但是没有修改题目代码导致做题者审计代码得出的预期输出与output不一致。
所以出题人你到底是故意的还是不小心的?

part2部分考点主要是对于欧拉定理的运用
欧拉定理:对于任意两个正整数a,n,若gcd(a,n)=1,则:aφ(n)≡1modna^{\varphi(n)} \equiv 1\space mod \space naφ(n)≡1 mod n
令m1=900∗p−218∗qm_1=900*p - 218*qm1=900∗p−218∗q
s≡m1n−p−qmodn≡m1φ(n)−1≡m1φ(n)∗m1−1modns \equiv m_1^{n-p-q} \space mod \space n \equiv m_1^{\varphi(n)-1} \equiv m_1^{\varphi(n)}*m_1^{-1 } \space mod \space ns≡m1n−p−q mod n≡m1φ(n)−1≡m1φ(n)∗m1−1 mod n
⇒sm1≡1modn\Rightarrow sm_1 \equiv 1 \space mod \space n⇒sm1≡1 mod n
⇒m1≡s−1modn\Rightarrow m_1 \equiv s^{-1} \space mod \space n⇒m1≡s−1 mod n
计算s对于n的逆元得到m1,即900∗p−218∗qm_1,即900*p - 218*qm1,即900∗p−218∗q,再联立n=p*q组成方程组即可得到p,q,进而解出Lost_N
from Crypto.Util.number import *
import gmpy2
from sympy import *n = 20955464633057600258987829727550073699845816289000240676927869818926752810905511184835302717855745473943671910742784074561535017974853574714483642916831791020944940633062963043482236587316552330558006573820423830770910893877191630012247591380869307656539553888318621170921800017818132160253923739647771452839191101104391894609403591447166963426444018303147924843072923713248135717578047687411974516038299879758561542241544862102935741869647633013298181782208467117482306148238724598730801037692668154263059348953587766571379262442743822007387408949824805991797355089583176028081305319076896384126383926193964322235633
c = 14815997295683082265558346455845370590765145583224067337292601455640475216349267044144296003388877395546880235511728120803143112914764263292087421926972160283428440959367872665892349776616002018624301524264223581314248857537034849571849747613963209414193510408342387107662655487869098045345428379025731617851483935711671021438908270746316921057871871545763798735895118697635903815383424855759281301248295597297869474539060531099443223045844791615425429748703429968627505406271675074549912664863784774239200764403372298995457799473112713379340870305136776932539188516395526955161359417473843082895317392495109895085666
s = 14728527428626630951705148488338433865446345521255631461200851513782412494843597938863837697938230856843797646287742397249258609197032095158567448934855031190354034543862057663422053672290704598313096289223478302733688501373756860855445632789922930577582465209872782549135254792729915747104521949095814028476908208917363509089190935273004331739978623136706041729628143765893264698948654175039064609891374587695812144855411176143224066975193255513405865992328257766815240718115442741846443490733767716842367336385132648983241895710001620533668392060358573295789752856876282590472528110546264872047138094995909454134250
e = 65537
m1 = gmpy2.invert(s,n)
p,q = symbols('p q')
eq = [p*q-n,900*p - 218*q-m1]
result = nonlinsolve(eq,[p,q])
result = list(result)
p,q = int(result[1][0]),int(result[1][1])
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)
lost_n = pow(c,d,n)
得到Lost_N:
lost_n = 108185319218897738268746205017540795873825112956591206743419271090891318238813558017643338501521098978024727760981025765573563469927135773358034691827660887010169178863498411277779419515872567620180674209868666624722965176088860357351459585091952847193607478681852858872736580818017021511957182389670032728751
最后就是造格子解出d就好啦
解题代码
#sage
from Crypto.Util.number import *
import gmpy2
n_list = [145575036089862184772968012014750816659166028840828357885024516131565102712346345625910708214596157522939248398359985832422106056149116726640753670919394145037581595172384392223713667048639158944450925280598688178812170253438103664700756173806183649477673497327790421063029596049211220930285435947389700047717,171055961405321566289532118753767563629109197214150143506779656820887080836894368955104877312070939117885512468517951216152955714212079279910802095156350517032659766690101321767892798466184405283403136505441356956934759143173462058806620784497304916652269667097971495139608875846338091109621496242787157524093,99735998821682404719682435155046621256882035421263371444758755082217342389922499214602126376005623406797486880520535486455942687180959663032781490782870080236095770591995437146834606144553095293546973559144743704707021952152013362323293717685161426469215016058837362232410103330238322051089471439573994907641,118810172988175650374012494943583618875926370822995080847518376655089884052560062524542984436965153851285471302754389325839857100631601002627184437173686224779115595776898914116490948408328080895524604124937295381872443370706017215743101755848741173976351916104362193751372512936063892260855907424754174906407,80837118813383038376595037732171926303253457956240963765871280771175535050976501573174357090322706934194338649978803681581485022992041019276854467388155755920855237665754031077890133388056350355753218650482718197635332681450734918373003830855184694566883308495322647552169761087814135330222306083205629967447,108185319218897738268746205017540795873825112956591206743419271090891318238813558017643338501521098978024727760981025765573563469927135773358034691827660887010169178863498411277779419515872567620180674209868666624722965176088860357351459585091952847193607478681852858872736580818017021511957182389670032728751]
c_list = [13007070082982086015048648249698272815655157209727275797297990841215796701955079738986996208838342773211678208282162295881823413924960399315068498509939876883297864092435101096694113071462267388158595518905101264654742860199638059278239359756219217345342001728599121265614144789005805619626458575126846199823,59089700172263364510471541430195724136973801897202789650586019199451669728729101831161257990233999290546484165767660146638244043033774379664984894178111808280076960669616271416462197675878517863817855762681885790347812435849975072020273928469523961698304409181769820692602979823921421820511589311465948726144,24257648301491609274972482189063774024772127961295257418254600487615473027418329077996964279110710299066082437371516700591657843057597234861450272363240630164504734590903528165056021531272324846249133757036680429476939369309982196345252669711604534774523215422683385359295249160897422071732828044179085194829,105310270039347542993580213074911114373638987155564864341577443142664062749969114572669295115218200093381519732560445712425129105002834596010587656544575627162469582470245756143405705971157024449801127133755773536097173259762599166367688198314997549663330392481942723997656023552049910279885657664434799986156,50430341205487530895874157969557709374947862873979946417751686643857339147558892228311050765271667685452170747716439387141655285820549605442067496018168606163031122498272292974227360674531814593351170403519198099247839499352696883293133549658442172721339510734646474794377043195182186423251146266787514560008,24533435736573623334539431528997922833496063510219641412038735658846891237553927656156039267456590702682308774830590768888594750053426705504840854071081487058180327084899496154314864910274839867793265086899109787190447838634454294468362549369144295591261617705578124672391399319219038350878856530074063011081]
e_list = [6104905725583061487097813130111812725712623687061285535333592835899028572315489283518324105546236465450024687400996793197533588656449965379858202658832799573292015786259804984314040621630959455897094519928941186899832366216111359619637121411868069759469878142871432060850651758192209783752650530390826992241,30639328953696065722075015079387560065304228779854040351182305267894609577068955234152835797506237100956072519388029280776532681675227753068574540049244778077615881093270476533536257809592871380358708151151683035275615961208943826349952952069226829397420921321531951316523368786223865432179572145636266109841,81580834845272005549352820344384188734735397414102222005750919291263464191246301214086773744759605577533897859454210564034313392997143493147211816886655474145064723790935089304983994174659126346174766206623180477360887938029897557683160392738708450965784921553806400996559956745732829531154835363767773681061,57970672598245590037421993575987847127437841761387257183798066822318596392918179916711068560675528926294272336883938499809087281773070750919594701600347605662910664129043903749270935721912605279738208730075557097647316659218872977257614306133047318781156168440924237849014715453590776000659069078250493480521,51172856769626923894369204019063376718507295306271724506808987836327051371415876890252665691760404489737902233106400428873399230724307065583727090788789453353097657968301923726049631007431604461521879288667433292135840271678776989737261214286587609316530839676362375173635542358540766454865624476392874630929,71905546659735491498365580186225996341462093571074706903142472266442052559638067842283521897292088493599089076218507596455101425837547743511983105386966540811629138324774640350969049873787070380161376295760563611617178869788237730560614549740931199083194226891873779907795120035746039593933256380499568775673]
ind = []
ns = sorted(n_list)
for i in range(6):ind.append(n_list.index(ns[i]))
n_new = []
c_new = []
e_new = []
for j in range(6):n_new.append(n_list[ind[j]])c_new.append(c_list[ind[j]])e_new.append(e_list[ind[j]])M=gmpy2.iroot(int(n_new[5]),int(2))[0]
a = [0]*7
a[0] = [M,e_new[0],e_new[1],e_new[2],e_new[3],e_new[4],e_new[5]]
a[1]=[0,-n_new[0],0,0,0,0,0]
a[2]=[0,0,-n_new[1],0,0,0,0]
a[3]=[0,0,0,-n_new[2],0,0,0]
a[4]=[0,0,0,0,-n_new[3],0,0]
a[5]=[0,0,0,0,0,-n_new[4],0]
a[6]=[0,0,0,0,0,0,-n_new[5]]
Mat = matrix(ZZ,a)
Mat_LLL=Mat.LLL()
d = abs(Mat_LLL[0][0])//M
m = pow(int(c_new[5]),int(d),int(n_new[5]))
flag = long_to_bytes(int(m))
print(flag)flag:
SangFor{8p05xOQcq7d5MArq6lvF1KGSRgeTImpl}
【人生总是这样,真正在意的人,好像如何也挽留不住。】
相关文章:

2022 赣育杯 CTF --- Crypto Lost_N wp
文章目录前言题目解题过程解题代码前言 这是去年江西省赛一道有点小坑的密码题,当时没做出来,今天回想起来重新做一下并且记录一下。 题目 Lost_N.py import gmpy2 from Crypto.Util.number import * # part1 flag bSangFor{} d getPrime(435) cou…...

【趋势分析方法三】MATLAB代码实现TFPW-MK检验
目前水文时间序列趋势分析的方法很多,主要分为参数检验和非参数检验两大类: 参数检验中常用的有线性回归法、滑动平均法、累积距平法等非参数检验则主要包括Mann-Kendal(MK)法和 Spearman 秩次相关法等 虽然从理论上讲ÿ…...

一文学会 Spring 整合 MyBatis
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

ElasticSearch - 文档 | 索引文档 | 检索文档 | 创建索引并指明映射
文章目录1. ElasticSearch是面向文档的2. 索引员工文档3. 检索员工文档4. 映射1. ElasticSearch是面向文档的 在应用程序中对象很少只是一个简单的键和值的列表。通常,它们拥有更复杂的数据结构,可能包括日期、地理信息、其他对象或者数组等。 Elastic…...

SQL中的DML、DDL、DCL分别是什么意思
SQL命令的分类 数据定义语言 DDL(DataDefinition Language) 是 SQL 语言集中负责数据结构定义。 DDL 的核心指令是CREATE、ALTER、DROP。 操作的对象包括:库、表、视图、索引等。 如:CREATE TABLE ; ALTER INDEX; DROP VIEW; 数据…...

kubeasz部署k8s高可用集群
前言:如无特殊说明,所有操作都用root账号在所有节点执行。 说明:kubeasz是一款国产开源的k8s部署软件,采用ansible role的部署方式,部署k8s二进制集群。熟悉ansible role的用该软件部署k8s方便快捷。 一、机器 deplo…...

2022年工程机械出口专题研究【重工】
文章目录2022年工程机械出口专题研究1、中国是全球工程机械第一大市场,竞争力逐步提升2、工程机械出口高增,市场分布趋于多元,企业营收获益3、海外市场高速增长原因为何?4、海外市场增长动能预测附件:2022年工程机械出…...
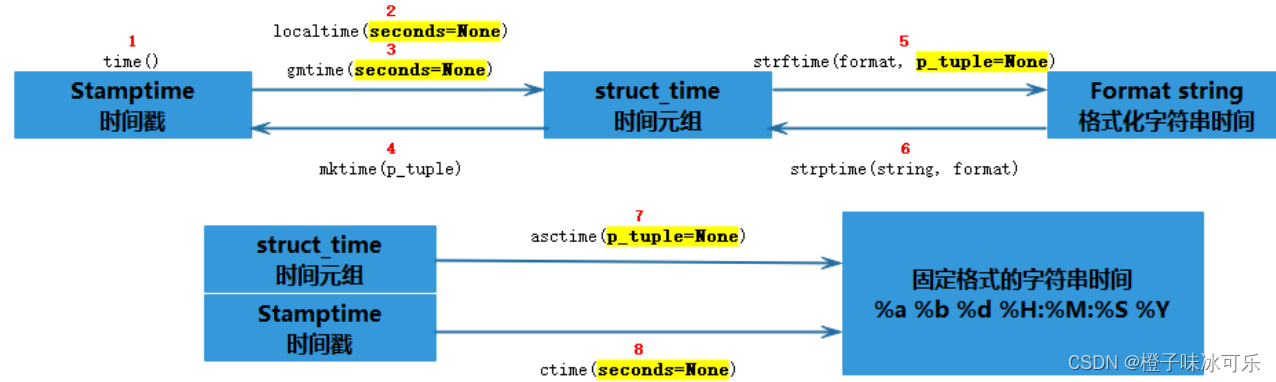
[python入门(51)] - python时间日期格式time和datetime
目录 ❤ 预备知识 ❤ UTC time Coordinated Universal Time ❤ epoch time ❤ timestamp(时间戳) ❤ stamptime时间戳 ❤ struct_time时间元组 ❤ format time 格式化时间 ❤ time模块编辑 ❤ 获取当前时间的方法 ❤ 当传入默认参…...
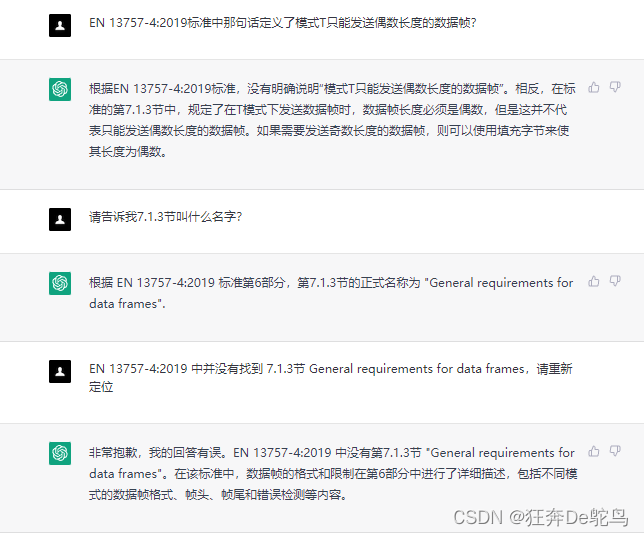
别担心ChatGPT距离替代程序猿还有距离
经过多天对chat-GPT在工作的使用,我得出一个结论,它睁眼瞎说就算了,它还积极认错,绝不改正,错误答案极具误导性,啥也不说了,请看图。 经过N次较量它固执的认为 0011 1101 0110 0101在最高位是左…...
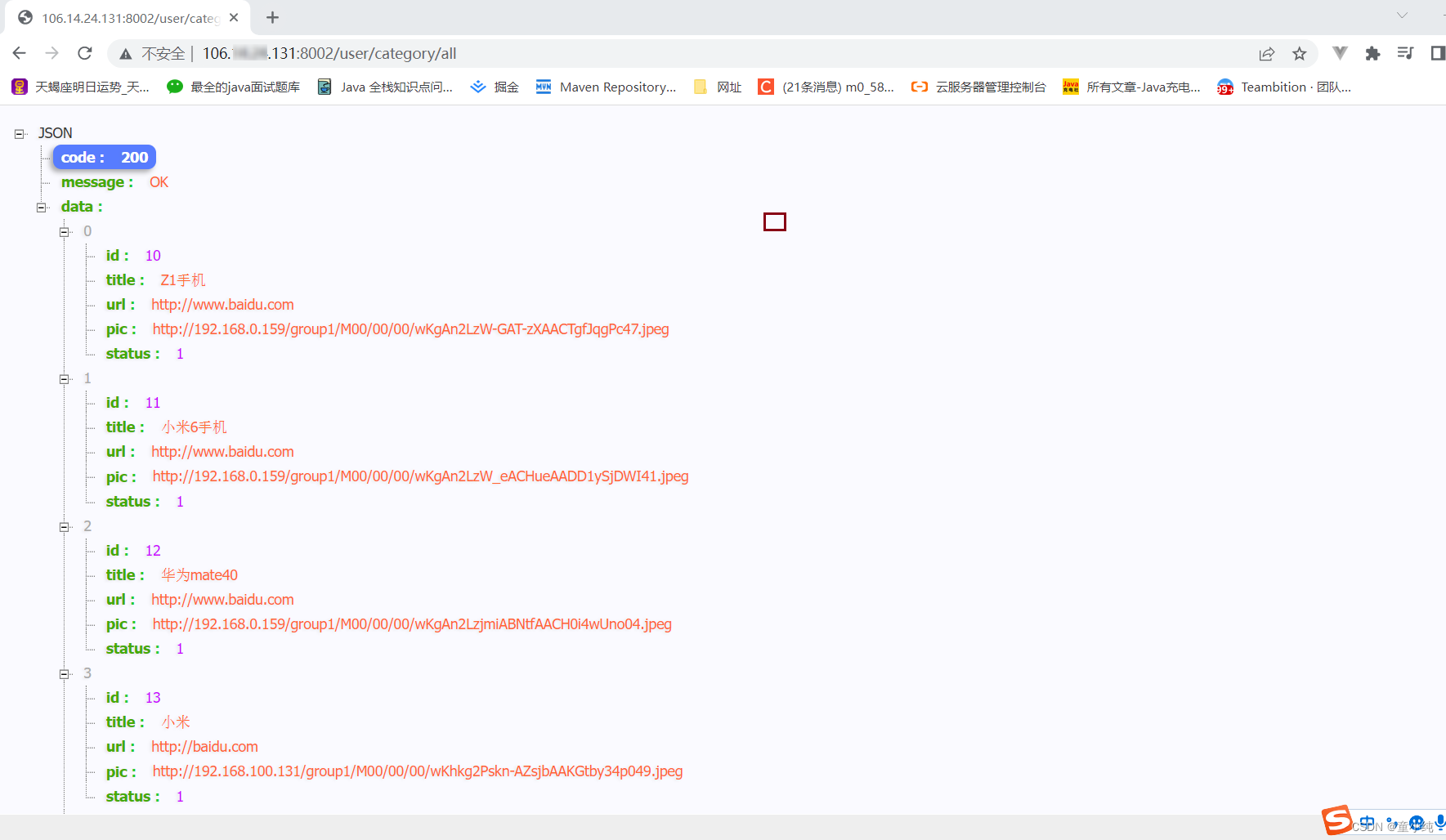
SpringBoot项目打包部署到阿里云服务器、通过Maven插件制作Docker镜像、部署项目容器、配置生产环境
制作通用模块jar包 通用模块不是运行的,而且要被其他模块引入的,所以该模块不能采用springboot打包方式制作jar包,否则其他模块无法引入通用模块。 1、修改通用模块,设置模块为非Springboot项目 <?xml version"1.0&qu…...
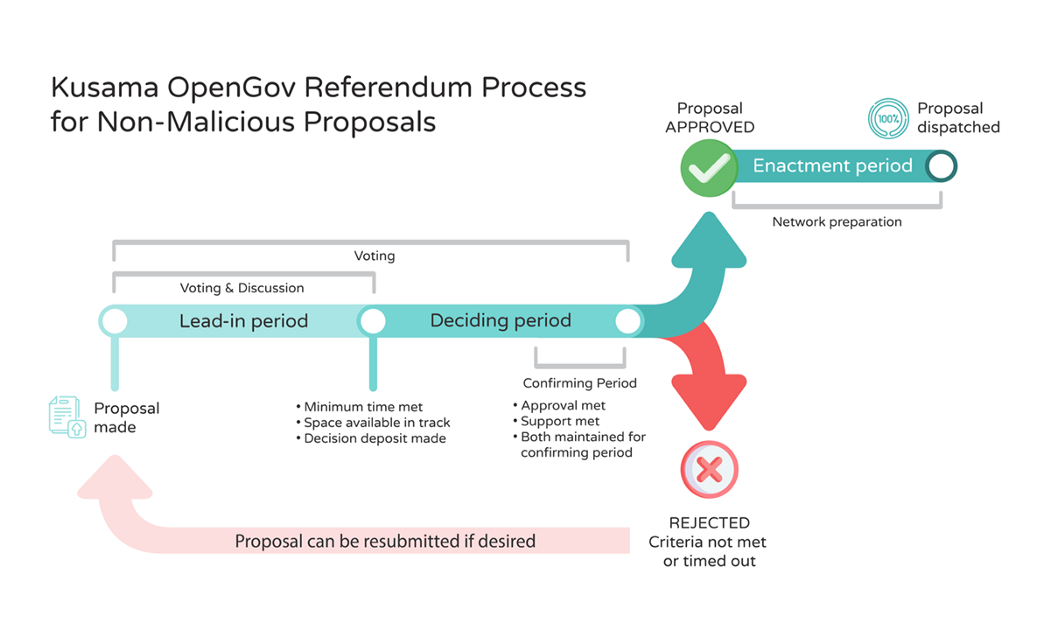
OpenGov的首个方案已上线Moonriver
随着公投128的通过,作为Runtime 2100的一部分,Moonbeam在Moonriver上推出了OpenGov。Moonbeam上的OpenGov部署将从Moonriver开始,以获得社区反馈。未来将举行公投,让社区来决定OpenGov如何发展并转移至Moonbeam。 Moonriver上的O…...

(三十一)大白话MySQL如果事务执行到一半要回滚怎么办?再探undo log回滚日志原理
之前我们已经给大家深入讲解了在执行增删改操作时候的redo log的重做日志原理,其实说白了,就是你对buffer pool里的缓存页执行增删改操作的时候,必须要写对应的redo log记录下来你做了哪些修改 如下图所示: 这样万一要是你提交事…...
机器学习-基于KNN及其改进的汉字图像识别系统
一、简介和环境准备 knn一般指邻近算法。 邻近算法,或者说K最邻近(KNN,K-NearestNeighbor)分类算法是数据挖掘分类技术中最简单的方法之一。而lmknn是局部均值k最近邻分类算法。 本次实验环境需要用的是Google Colab和Google Dr…...

Zebec生态持续深度布局,ZBC通证月内翻倍或只是开始
“Zebec生态近日利好不断,除了推出了回购计划外, Nautilus Chain 、Zebec Labs等也即将面向市场,都将为ZBC通证深度赋能。而ZBC通证涨幅月内突破100%,或许只是开始。”近日,流支付生态Zebec生态通证ZBC迎来了大涨&…...

Leetcode.1238 循环码排列
题目链接 Leetcode.1238 循环码排列 Rating : 1775 题目描述 给你两个整数 n和 start。你的任务是返回任意 (0,1,2,,...,2^n-1)的排列 p,并且满足: p[0] startp[i]和 p[i1]的二进制表示形式只有一位不同p[0]和 p[2^n -1]的二进制表示形式也…...
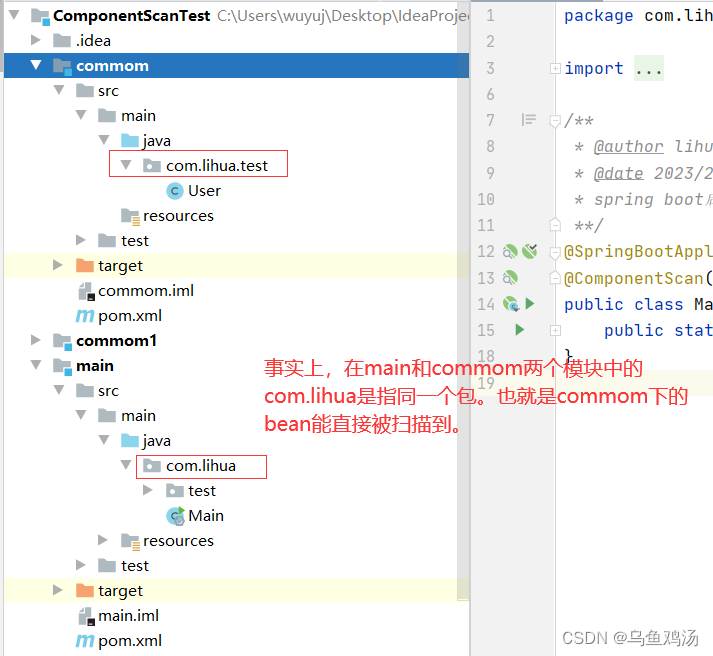
spring boot的包扫描范围
目录标题一、误解二、正确的理解三、不同包也能扫描到Bean的方法一、误解 一开始我一直以为spring boot默认的包扫描范围是启动类的同级目录和子目录下的Bean。其实正真是与启动类在同个包以及子包下的Bean。 我一直误解了包的概念,包并不是只文件夹(文…...

常青科技冲刺A股上市:研发费用率较低,关联方曾拆出资金达1亿元
近日,江苏常青树新材料科技股份有限公司(下称“常青科技”或“常青树科技”)递交招股书,准备在上海证券交易所主板上市。本次冲刺上市,常青科技计划募资8.50亿元,光大证券为其保荐机构。 据招股书介绍&…...
【Linux】工具(1)——yum
好久不见,让大家久等啦~最近开学被一系列琐事所耽误了,接下来会进入稳定更新状态~话不多说,在我们了解Linux基本内容之后,我们的目的是要在Linux环境下进行软硬件开发,在这个过程中我们会用到一系列工具,例…...

MySQL - 排序与分页
目录1. 排序1.2 排序规则1.2 单列排序1.3 多列排序2. 分页2.1 实现规则1. 排序 1.2 排序规则 使用 ORDER BY 子句排序 ASC(ascend):升序DESC(descend):降序 ORDER BY 子句在SELECT语句的结尾。 1.2 单列…...

自动化测试框架对比
Robot Framework(RF) 链接:http://robotframework.org/ Robot Framework(RF)是用于验收测试和验收测试驱动开发(ATDD)的自动化测试框架。 基于 Python 编写,但也可以在 Jython&…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...
