图像处理与计算机视觉--第五章-图像分割-霍夫变换
文章目录
- 1.霍夫变换(Hough Transform)原理介绍
- 2.霍夫变换(Hough Transform)算法流程
- 3.霍夫变换(Hough Transform)算法代码
- 4.霍夫变换(Hough Transform)算法效果
1.霍夫变换(Hough Transform)原理介绍
Hough Transform是一种常用的计算机视觉图形检验方法,霍夫变换一般用于检验直线或者圆。
霍夫变换的原理具体如下所示:
假设图像中存在一条直线,表达式如下所示:
y = k x + b y=kx+b y=kx+b
假设我们任意指定一个点 ( x 0 , y 0 ) (x_{0},y_{0}) (x0,y0),则对于任意穿过该点的直线,一定有如下公式成立:
b = − k x 0 + y 0 b=-kx_{0}+y_{0} b=−kx0+y0
此时我将以x,y为轴的图像变为以b,k为轴的图像,此时该直线也能够进行变化,并且如上推导可知,对应的图像也是一条直线,如图所示:
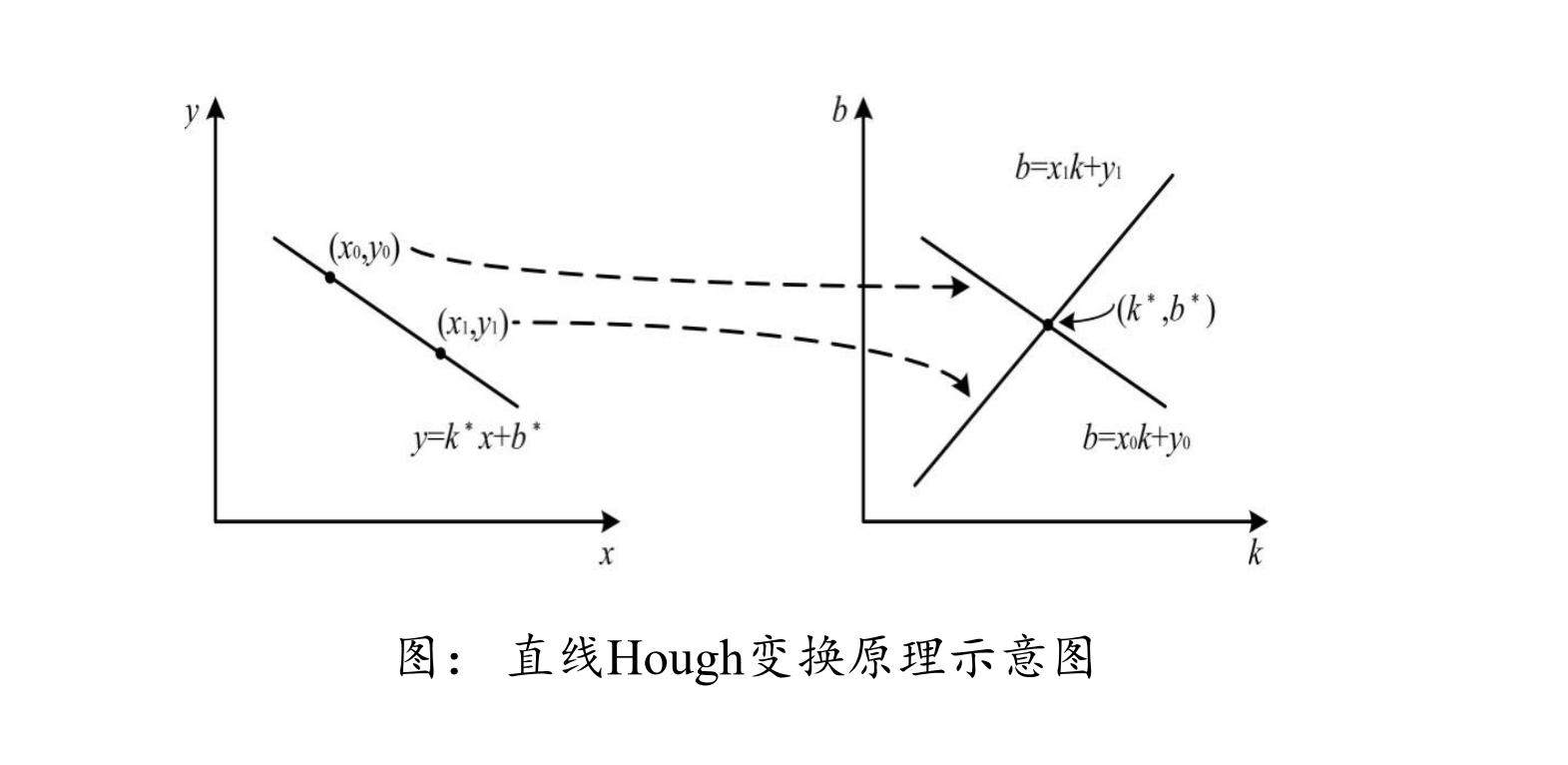
进一步的,我们再从直线上取一点 ( x 1 , y 1 ) (x_{1},y_{1}) (x1,y1),则必有如下公式:
b = − k x 1 + y 1 b=-kx_{1}+y_{1} b=−kx1+y1
在图像上绘制会这样的函数,我们可知,两条直线相交于一点 ( k ∗ , b ∗ ) (k^{*},b^{*}) (k∗,b∗),而这个点就是x,y轴上的 ( x 1 , y 1 ) (x_{1},y_{1}) (x1,y1)和 ( x 0 , y 0 ) (x_{0},y_{0}) (x0,y0)两点所确定的直线。

但是我们在实际的直线检测中,我们不会用到上述的坐标系方法,上述的方法只是提供一个求解的思路,我们将使用极坐标方程来完成上述方法的求解,对于上述的直线,极坐标方程可以表示为:
ρ = x c o s θ + s i n θ \rho=xcos\theta+sin\theta ρ=xcosθ+sinθ
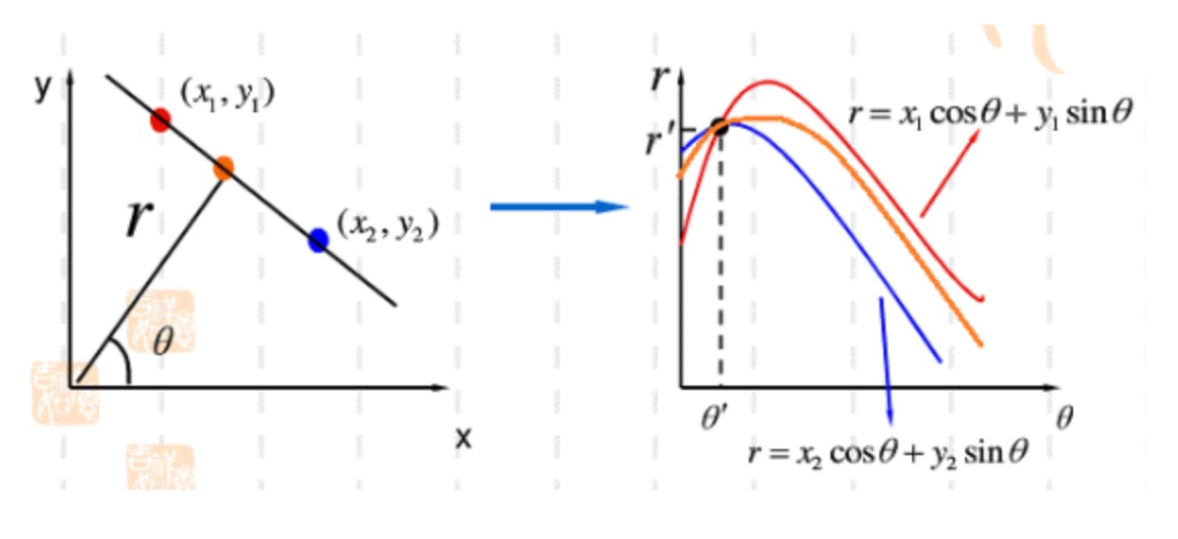
其中, θ \theta θ为直线的法线向量与x轴正向的夹角,而 ρ \rho ρ为坐标系原点至直线的垂直距离,如下图所示:
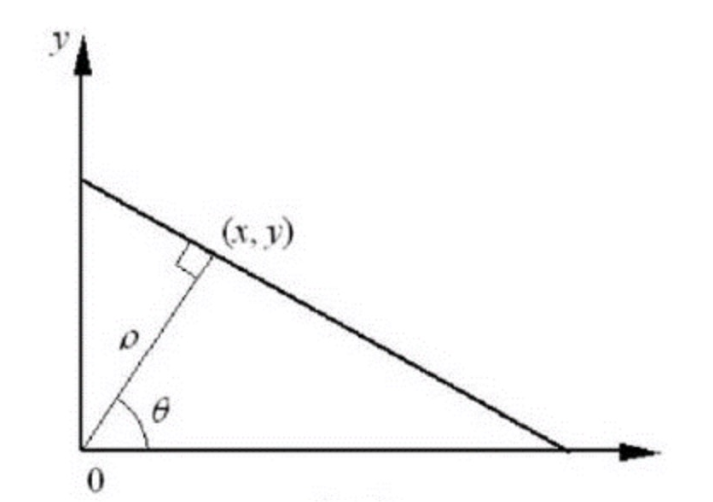
如下所示,我们可以发现,这条直线在极坐标下只有一个( ρ \rho ρ, θ \theta θ) 与之对应,改变一个参数大小变换到空域上的直线即会改变。而空域这条直线上的所有点都可以在极坐标为( ρ \rho ρ, θ \theta θ) 所表示的直线上 (如下图所示)
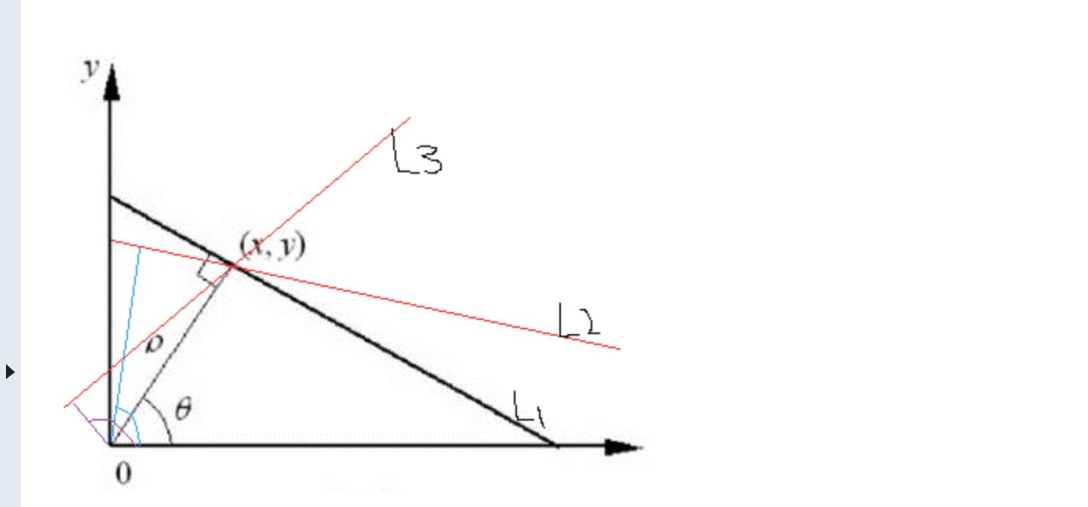
空域直线上的一个点在极坐标系下具体对应多少个极坐标对,取决于 θ \theta θ的步长 ,如果设步长为 β \beta β,则极坐标对n的表示如下所示:
n = 360 β n=\frac{360}{\beta} n=β360
对应的图片如下所示:
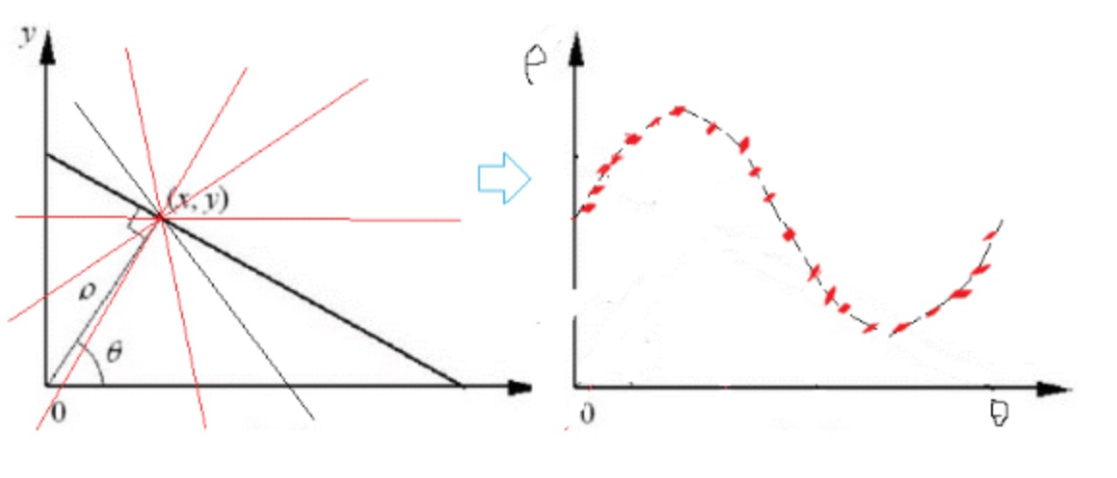
接下来我们假设空域上的三个点对应的极坐标曲线如下图的(a)所示,极坐标曲线同时经过一个点表示空域下有一条直线经过这三个点,只要寻找交点最多的点,在空域内就是要寻找的直线。
2.霍夫变换(Hough Transform)算法流程
·Hough变换直线检测的步骤如下:
1.设0的取值范围为[0,360],单位为度根据检测精度要求,采取适当的步长对角度和长度的取值范围进行离散化,形成0-p平面上的离散网格。
2.将每一个离散网格视为一个投票累加器,初始时全部清0。
3.遍历图像的所有像素,对于每个像素计算离散值0i和p=xcos0+ysin0.
4.对在参数空间中将对应的累加器中的值加1,从而完成求出相应的离散化值p,对于每个(p,0)该像素点的投票的投票之后,在离散化的参数空间中找出所累积的投票值
5.访问完所有的图像像素并完成所有,点这些点所对应的参数即为检测得到的直线的参数大于某给定闽值T的局部极大值点,
3.霍夫变换(Hough Transform)算法代码
import numpy as np
import cv2
from PIL import Image,ImageEnhance
import matplotlib.pyplot as plt
"""
hough变换是一种常用的计算机视觉图形检验方法,霍夫变换一般用于检验直线或者圆。"""
img = Image.open(r"C:\Users\Zeng Zhong Yan\Desktop\py.vs\python学习\test.webp")
#增强图像效果
img = ImageEnhance.Contrast(img).enhance(3)
img.show()
#处理成矩阵,便于后续处理
img = np.array(img)
#灰度处理
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
#cv2.THRESH_OTSU具有双峰值,显示效果更好.
"""
cv2.THRESH_OTSU使用最小二乘法处理像素点。一般情况下,cv2.THRESH_OTSU适合双峰图。
cv2.THRESH_TRIANGLE使用三角算法处理像素点。一般情况下,cv2.THRESH_TRIANGLE适合单峰图。
"""
ret, thresh = cv2.threshold(gray, 0, 255, cv2.THRESH_OTSU)
#canny边缘检验算法处理
result = cv2.Canny(thresh, ret-30, ret+30, apertureSize=3)#霍夫变换检测直线
lines = cv2.HoughLinesP(result, 1, 1 * np.pi / 180, 10, minLineLength=10, maxLineGap=5)
# 画出检测的线段
for line in lines:for x1, y1, x2, y2 in line:cv2.line(img, (x1, y1), (x2, y2), (255, 0, 0),2)
img = Image.fromarray(img, 'RGB')
img.show()
4.霍夫变换(Hough Transform)算法效果
1.原先的图片如下所示:

2.霍夫变换后的检测直线的效果

相关文章:

图像处理与计算机视觉--第五章-图像分割-霍夫变换
文章目录 1.霍夫变换(Hough Transform)原理介绍2.霍夫变换(Hough Transform)算法流程3.霍夫变换(Hough Transform)算法代码4.霍夫变换(Hough Transform)算法效果 1.霍夫变换(Hough Transform)原理介绍 Hough Transform是一种常用的计算机视觉图形检验方法,霍夫变换一…...

linux下文件操作命令
title: linux下文件操作命令 createTime: 2020-10-29 18:05:52 updateTime: 2020-10-29 18:05:52 categories: linux tags: Linux下文件操作命令 tar命令 使用tar命令一般打包分为两种*.tar ,*.tar.gz 相信大家也使用过tar -zcvf test.tar test/tar -zcvf test.tar.gz test/…...

Golang语法、技巧和窍门
Golang简介 命令式语言静态类型语法标记类似于C(但括号较少且没有分号),结构类似Oberon-2编译为本机代码(没有JVM)没有类,但有带有方法的结构接口没有实现继承。不过有type嵌入。函数是一等公民函数可以返…...
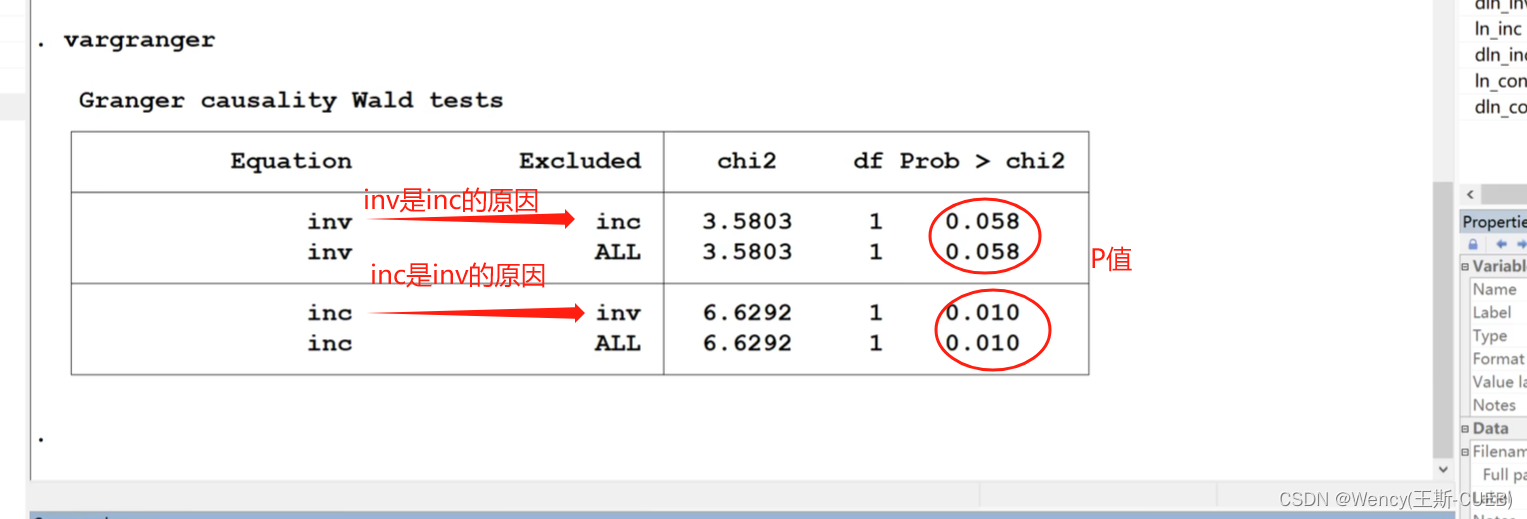
Grander因果检验(格兰杰)原理+操作+解释
笔记来源: 1.【传送门】 2.【传送门】 前沿原理介绍 Grander因果检验是一种分析时间序列数据因果关系的方法。 基本思想在于,在控制Y的滞后项 (过去值) 的情况下,如果X的滞后项仍然有助于解释Y的当期值的变动,则认为 X对 Y产生…...
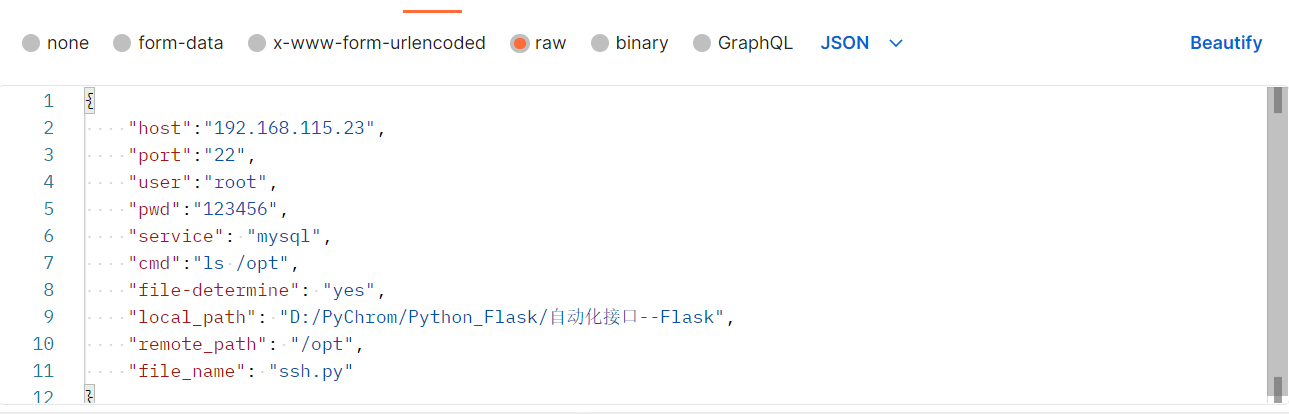
Python-Flask:编写自动化连接demo脚本:v1.0.0
主函数: # _*_ Coding : UTF-8 _*_ # Time : 13:14 # Author : YYZ # File : Flask # Project : Python_Project_爬虫 import jsonfrom flask import Flask,request,jsonify import sshapi Flask(__name__)# methods: 指定请求方式 接口解析参数host host_info[…...
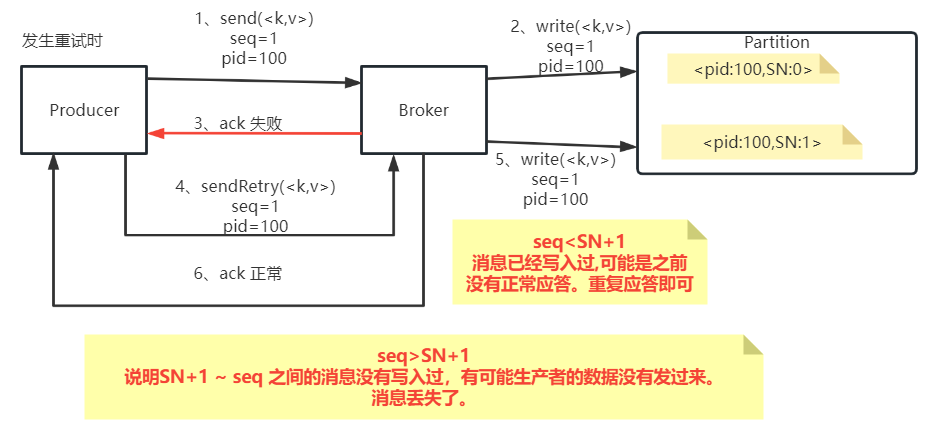
kafka客户端应用参数详解
一、基本客户端收发消息 Kafka提供了非常简单的客户端API。只需要引入一个Maven依赖即可: <dependency><groupId>org.apache.kafka</groupId><artifactId>kafka_2.13</artifactId><version>3.4.0</version></depend…...

Apache Doris 行列转换可以这样玩
行列转换在做报表分析时还是经常会遇到的,今天就说一下如何实现行列转换吧。 行列转换就是如下图所示两种展示形式的互相转换 1. 行转列 我们来看一个简单的例子,我们要把下面这个表的数据,转换成图二的样式 image-20230914151818953.png …...
及键盘事件、右键事件)
【Qt图形视图框架】自定义QGraphicsItem和QGraphicsView,实现鼠标(移动、缩放)及键盘事件、右键事件
自定义QGraphicsItem和QGraphicsView 说明示例myitem.hmyitem.cppmyview.hmyview.cpp调用main.cpp 效果 说明 在使用Qt的图形视图框架实现功能时,一般会在其基础上进行自定义功能实现。 如:滚轮对场景的缩放,鼠标拖动场景中的项,…...
C语言结构体指针学习
结构体变量存放内存中,也有起始地址,定义一个变量来存放这个地址,那这个变量就是结构体指针; typedef struct mydata{int a1;int a2;int a3; }mydata;void CJgtzzView::OnDraw(CDC* pDC) {CJgtzzDoc* pDoc GetDocument();ASSERT…...
华为云云耀云服务器L实例评测|部署在线轻量级备忘录 memos
华为云云耀云服务器L实例评测|部署在线轻量级备忘录 memos 一、云耀云服务器L实例介绍1.1 云服务器介绍1.2 产品优势1.3 应用场景1.4 支持镜像 二、云耀云服务器L实例配置2.1 重置密码2.2 服务器连接2.3 安全组配置 三、部署 memos3.1 memos介绍3.2 Docker 环境搭建…...
详解Avast Driver Updater:电脑驱动更新工具的利器还是多余的软件?
亲爱的读者朋友们,你是不是经常为电脑的驱动问题而烦恼?如果是的话,你可能会对这款软件——Avast Driver Updater 电脑驱动更新工具感兴趣。但在你决定尝试之前,不妨先和我一起深入探讨一下它的优点、缺点以及它适用的使用场景。 …...

大数据Flink(九十五):DML:Window TopN
文章目录 DML:Window TopN DML:Window TopN Window TopN 定义(支持 Streaming):Window TopN 是一种特殊的 TopN,它的返回结果是每一个窗口内的 N 个最小值或者最大值。 应用场景...

使用OKHttpClient访问网络
使用OKHttpClient前要引入依赖: 在build.gradle(Moduel :app)中添加 implementation com.squareup.okhttp3:okhttp:3.14.1 implementation com.squareup.okhttp3:logging-interceptor:3.14.1 implementation com.squareup.okio:okio:1.6.0 1. GET(同步…...

maui 开发AMD CPU踩的坑。
刚换的 amd R7735HS 笔记本,8核16线程,32GB内存。性能得实强悍 。 当需要发布iOS版本时发现,我没有macos ,那就安装个vmware 吧。看了一下Apple 要求以后的发布的APP需要以xcode14.3或以后版本开发的版本,但xcode14.3…...
宝塔反代openai官方API接口详细教程,502 Bad Gateway问题解决
一、前言 宝塔反代openai官方API接口详细教程,实现国内使用ChatGPT502 Bad Gateway问题解决, 此方法最简单快捷,没有复杂步骤,不容易出错,即最简单,零代码、零部署的方法。 二、实现前提 一台海外VPS服务…...

【leetocde】128. 最长连续序列
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 示例 1: 输入:nums [100,4,200,1,3,2] 输出:4 …...

【Vue3】动态 class 类
如果你想在 Vue.js 中动态设置元素的 class 类名,你可以使用以下两种主要方式: 绑定一个动态的 class 对象:你可以使用 v-bind 或简写的 : 来绑定一个包含类名的对象,其中类名的键是类名字符串,值是一个布尔值或计算属…...
【Redis】redis基本数据类型详解(String、List、Hash、Set、ZSet)
目录 RedisString(字符串)List(列表)Hash(字典)Set(集合)ZSet(有序集合) Redis Redis有5种基本的数据结构,分别为:string(字符串)、list(列表)、set(集合)、hash(哈希&a…...

ubuntu源码安装aria2
github:GitHub - aria2/aria2: aria2 is a lightweight multi-protocol & multi-source, cross platform download utility operated in command-line. It supports HTTP/HTTPS, FTP, SFTP, BitTorrent and Metalink. 发行说明:GitHub - aria2/aria2 at releas…...

【多任务案例:猫狗脸部定位与分类】
【猫狗脸部定位与识别】 1 引言2 损失函数3 The Oxford-IIIT Pet Dataset数据集4 数据预处理4 创建模型输入5 自定义数据集加载方式6 显示一批次数据7 创建定位模型8 模型训练9 绘制损失曲线10 模型保存与预测 1 引言 猫狗脸部定位与识别分为定位和识别,即定位猫狗…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
