【数据结构】排序(2)—冒泡排序 快速排序
目录
一. 冒泡排序
基本思想
代码实现
时间和空间复杂度
稳定性
二. 快速排序
基本思想
代码实现
hoare法
挖坑法
前后指针法
时间和空间复杂度
稳定性
一. 冒泡排序
基本思想
冒泡排序是一种交换排序。两两比较数组元素,如果是逆序(即排列顺序与排序后的顺序相 反)就交换,直到所有元素都有序为止。
方法步骤:
① 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
② 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后 的元素会是最大的数。
③ 针对所有的元素重复以上的步骤,除了最后一个。
④ 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
图示

代码实现
//冒泡排序
void BubbleSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int flag = 0; //作为判断是否交换的标志for (int j = 1; j < n - i; j++){if (a[j-1] > a[j]){flag = 1;int tmp = a[j-1]; //交换a[j-1] = a[j];a[j] = tmp;}}if (flag == 0)break;}
}时间和空间复杂度
若初始序列为正序序列,则只需进行一趟排序,在排序过程中进行n-1次比较,不移动元素;若初始序列为逆序序列,则需进行n-1趟排序,n(n-1) / 2次比较,每次比较都需要移动 3 次,移动次数为 3n(n-1) / 2.
时间复杂度:O(n^2)
空间复杂度:O(1)
稳定性
冒泡排序:稳定排序
二. 快速排序
基本思想
任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止
方法步骤:
-
从数列中挑出一个元素,称为 "基准"(pivot);
-
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
-
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;
图示
代码实现
hoare法
思想方法:
定义两个指针 left 和 right,分别指向左边和右边,左指针从左向右找大( 大于pivotkey),右 指针从右向左找小(小于pivotkey),左大右小就交换,相遇时与基准值交换
图解:

int PartSort(int* a, int left, int right) //给数组分区,返回枢轴元素下标
{int pivotkey = left;while (left < right){//右边找比pivotkey小的while (left < right && a[right] >= a[pivotkey])right--;//左边找比pivotkey大的while (left < right && a[left] <= a[pivotkey])left++;Swap(&a[left], &a[right]);}Swap(&a[left], &a[pivotkey]); //把记录的枢轴元素,交换到枢轴位置return left; //返回枢轴所在的位置下标
}
挖坑法
思想方法:
定义两个指针 left 和 right,分别指向左边和右边,先将第一个数据元素放在临时变量 pivotkey 中,形成一个坑位;让右指针先走,当指向的值小于 pivotkey 就停下,形成新的坑位;让左指针走,当指向的值大于 pivotkey 就停下,使其形成此次的新坑位,直到两指针相遇,把pivotkey的值放入坑中。
图解:

int PartSort(int* a, int left, int right) //给数组分区,返回枢轴元素下标
{int pivotkey = a[left]; //保存第一个数据元素的值while (left < right){while (left < right && a[right] >= pivotkey) //找小{right--;}a[left] = a[right]; //右边形成新的坑while (left < right && a[left] <= pivotkey) //找大{left++;}a[right] = a[left]; //左边形成新的坑}a[left] = pivotkey;return left;
}前后指针法
思想方法:
定义两个指针 prev 和 cur ,初始时,prev指针指向序列开头,cur指针指向prev指针的后一个位置;cur的值与pivotkey的值比较,cur的值小,prev先后移一步,cur再后移;当cur的值大时,就prev的值与cur的值交换;直到cur为空时,prev的值与pivotkey的值交换。
图解:
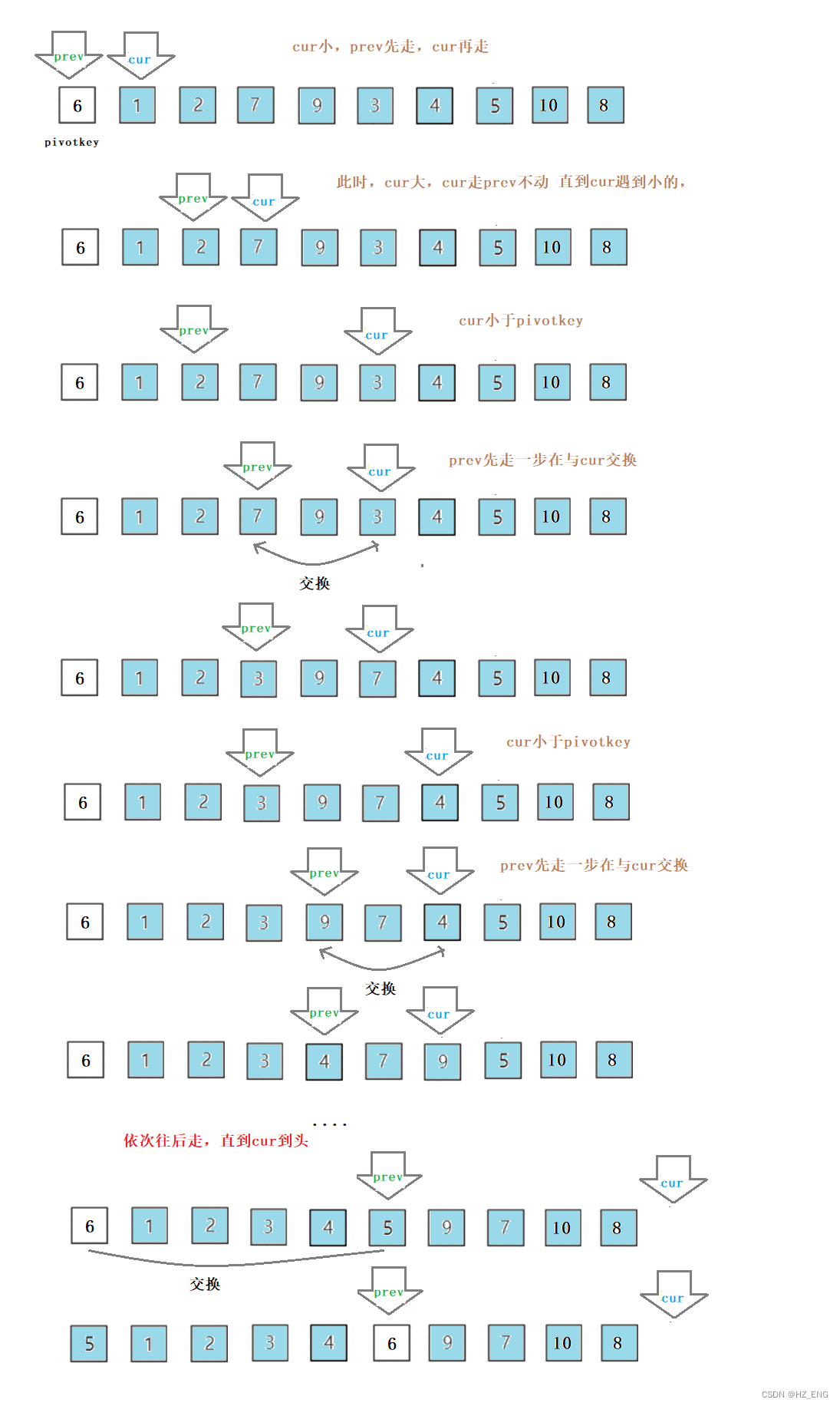
int PartSort(int* a, int left, int right) //给数组分区,返回枢轴元素下标
{int prev = left;int cur = left + 1;int pivotkey = left;while (cur <= right){if (a[cur] < a[pivotkey] && ++prev != cur)Swap(&a[cur], &a[prev]);cur++;}Swap(&a[pivotkey], &a[prev]);return prev;
}
时间和空间复杂度
在最优情况下,partition每次都划的很均匀,此时时间复杂度为O(nlogn);平均情况下,其时 间复杂度也为O(nlogn)。在最坏的情况下,待排序的序列为正序或逆序时,递归树是一棵斜树, 此时,快速排序会堕落为冒泡排序,其时间复杂度为O(n^2),不过可以通过优化,使其提升为O(nlogn),总的来说还是O(nlogn)。
空间复杂度,主要是递归造成的栈空间的使用,最好情况及平均情况下,树的递归深度为logn,空间复杂度均为O(logn);最坏情况,空间复杂度为O(n).
时间复杂度:O(nlogn)
空间复杂度:O(logn)
稳定性
由于元素的比较和交换是跳跃进行的,因此
快速排序:不稳定排序
相关文章:

【数据结构】排序(2)—冒泡排序 快速排序
目录 一. 冒泡排序 基本思想 代码实现 时间和空间复杂度 稳定性 二. 快速排序 基本思想 代码实现 hoare法 挖坑法 前后指针法 时间和空间复杂度 稳定性 一. 冒泡排序 基本思想 冒泡排序是一种交换排序。两两比较数组元素,如果是逆序(即排列顺序与排序后…...

Redis与分布式-分布式锁
接上文 Redis与分布式-集群搭建 1.分布式锁 为了解决上述问题,可以利用分布式锁来实现。 重新复制一份redis,配置文件都是刚下载时候的不用更改,然后启动redis服务和redis客户。 redis存在这样的命令:和set命令差不多࿰…...

docker安装nginx详解
创建html的挂载目录docker volume create nginx8020 创建conf的挂载目录mkdir -p /opt/nginx/conf 拉取镜像docker pull nginx 初始化挂载目录的配置文件docker run --rm --name nginx-short -p 8020:80 -d nginx docker cp nginx-short:/etc/nginx/nginx.conf /opt/nginx/…...

优化思考二
优化思考一_云湖在成长的博客-CSDN博客 翻到了两年前写文章,有了不一样的观点。 先说一样的想法吧:数据(输入)>>优化模型(处理)>>结果方案(输出)。优化是其中最重要的…...

大模型微调概览
文章目录 微调 和 高效微调高效微调技术方法概述高效微调方法一:LoRA高效微调方法二: Prefix Tuning高效微调方法三: Prompt Tuning高效微调方法四: P-Tuning v2基于强化学习的进阶微调方法RLHF 训练流程微调 和 高效微调 微调,Fine-Tuning, 一般指全参数的微调(全量微调),…...

利用norm.ppfnorm.interval分别计算正态置信区间[实例]
scipy.stats.norm.ppf用于计算正态分布的累积分布函数CDF的逆函数,也称为百分位点函数。它的作用是根据给定的概率值,计算对应的随机变量值。scipy.stats.norm.interval:用于计算正态分布的置信区间,可指定均值和标准差。scipy.st…...

计算机网络各层设备
计算机网络通常被分为七层,每一层都有对应的设备。以下是各层设备的简要介绍: 物理层(Physical Layer):负责传输二进制数据位流的物理媒体和设备,例如网线、光纤、中继器、集线器等。 数据链路层…...

java this用法
在Java中,this是一个关键字,表示当前对象。它可以用来引用当前对象的实例变量、实例方法或者调用当前对象的构造方法。在本文中,我们将深入探讨Java中this关键字的用法。 1. 引用当前对象的实例变量 在Java中,this关键字可以用来…...

【AI视野·今日NLP 自然语言处理论文速览 第四十六期】Tue, 3 Oct 2023
AI视野今日CS.NLP 自然语言处理论文速览 Tue, 3 Oct 2023 (showing first 100 of 110 entries) Totally 100 papers 👉上期速览✈更多精彩请移步主页 Daily Computation and Language Papers Its MBR All the Way Down: Modern Generation Techniques Through the …...

Unity ddx与ddy
有关Unity的dx与dy的概念 引用的文章 1link 2link 3link 4link 有关概念 我们知道在光栅化的时刻,GPUs会在同一时刻并行运行很多Fragment Shader,但是并不是一个pixel一个pixel去执行的,而是将其组织在2x2的一组pixels分块中,…...

bootstrap.xml 和applicaiton.properties和applicaiton.yml的区别和联系
当谈到Spring Boot应用程序的配置时,有三个关键文件经常被提到:bootstrap.xml、application.properties和application.yml。这些文件在应用程序的不同阶段起着不同的作用,并在配置应用程序属性时有一些区别和联系。本文将探讨这些文件的作用、…...
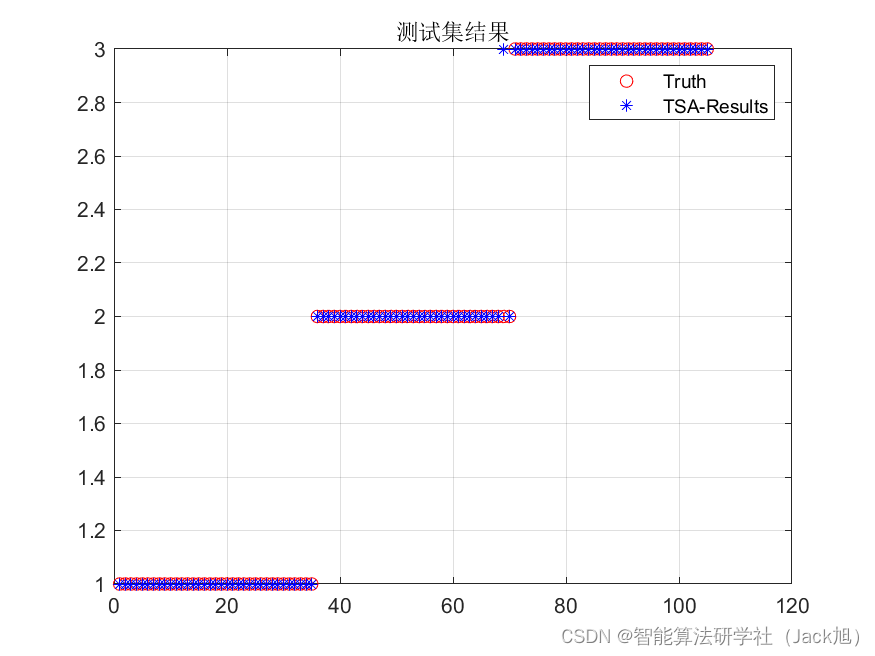
基于被囊群优化的BP神经网络(分类应用) - 附代码
基于被囊群优化的BP神经网络(分类应用) - 附代码 文章目录 基于被囊群优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.被囊群优化BP神经网络3.1 BP神经网络参数设置3.2 被囊群算法应用 4.测试结果&#x…...
我的第一个react.js 的router工程
react.js 开发的时候,都是针对一个页面的,多个页面就要用Router了,本文介绍我在vscode 下的第一个router 工程。 我在学习react.js 前端开发,学到router 路由的时候有点犯难了。经过1-2天的努力,终于完成了第一个工程…...

XXPermissions权限请求框架
官网 项目地址:Github博文地址:一句代码搞定权限请求,从未如此简单 框架亮点 一马当先:首款适配 Android 13 的权限请求框架简洁易用:采用链式调用的方式,使用只需一句代码体积感人:功能在同类…...

远程代码执行渗透测试—Server2128
远程代码执行渗透测试 任务环境说明: √ 服务器场景:Server2128(开放链接) √服务器场景操作系统:Windows √服务器用户名:Administrator密码:pssw0rd 1.找出靶机桌面上文件夹1中的文件RCEBac…...

阿里云关系型数据库有哪些?RDS云数据库汇总
阿里云RDS关系型数据库大全,关系型数据库包括MySQL版、PolarDB、PostgreSQL、SQL Server和MariaDB等,NoSQL数据库如Redis、Tair、Lindorm和MongoDB,阿里云百科分享阿里云RDS关系型数据库大全: 目录 阿里云RDS关系型数据库大全 …...

Linux--socket编程--服务端代码
查看struct sockaddr_in包含的东西: 在/user/include下搜索:grep "struct sockaddr_in { " * -nir r : 递归 i : 不区分大小写 n : 显示行号 socket编程–服务端代码 /* 1、调用 socket 创建套接字 2、调用 bind 添加地址 3、lis…...
安装Vue脚手架图文详解教程
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl 预备工作 在安装Vue脚手架之前,请确保您已经正确安装了npm;假若还尚未安装npm,请你参考 Node.js安装教程图文详解。 安装Vue脚手架 请…...
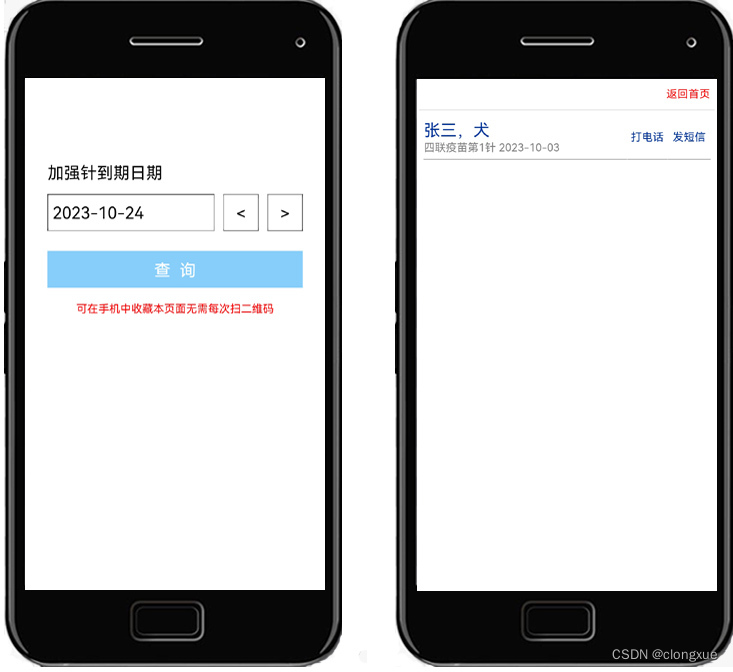
宠物医院必备,介绍一款宠物疫苗接种管理软件
在当今社会,养宠物已经成为越来越多人的生活方式,宠物疫苗接种已是宠物医院的重要工作,但是目前绝大多数的宠物医院对疫苗接种的管理,还是采取人工登记方式,不仅效率低下,而且无法做到疫苗接种到期自动提醒…...
哈哈,我保研985了,之后会出一期保研经验分享
哈哈,我保研了,之后会出一期保研经验分享 个人背景 学校:河南某四非,计算机科学与技术专业英语成绩:四级439,六级438(夏令营无六级)科研经历:一个软著、国家级大创&…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...

spring boot使用HttpServletResponse实现sse后端流式输出消息
1.以前只是看过SSE的相关文章,没有具体实践,这次接入AI大模型使用到了流式输出,涉及到给前端流式返回,所以记录一下。 2.resp要设置为text/event-stream resp.setContentType("text/event-stream"); resp.setCharacter…...
