AcWing算法提高课-5.6.1同余方程
宣传一下 算法提高课整理
CSDN个人主页:更好的阅读体验

原题链接
题目描述
求关于 x x x 的同余方程 a x ≡ 1 ( m o d b ) ax ≡ 1 \pmod b ax≡1(modb) 的最小正整数解。
输入格式
输入只有一行,包含两个正整数 a , b a,b a,b,用一个空格隔开。
输出格式
输出只有一行,包含一个正整数 x x x,表示最小正整数解。
输入数据保证一定有解。
数据范围
2 ≤ a , b ≤ 2 × 1 0 9 2 \le a,b \le 2 \times 10^9 2≤a,b≤2×109
输入样例:
3 10
输出样例:
7
思路
我们对 a x ≡ 1 ( m o d b ) ax ≡ 1 \pmod b ax≡1(modb) 进行变形:
设 y ∈ R y \in \mathbb{R} y∈R,则:
a x ≡ 1 ( m o d b ) ⇔ a x − b y = 1 ax \equiv1 \pmod b \Leftrightarrow ax-by=1 ax≡1(modb)⇔ax−by=1
我们知道,扩展欧几里得算法可以计算形如 a x + b y = gcd ( a , b ) ax+by=\gcd(a,b) ax+by=gcd(a,b) 的方程的解。
所以直接进行转化即可。
注意: 由于题目要求输出正整数解,所以我们输出 ( x m o d p + p ) m o d p (x \bmod p + p) \bmod p (xmodp+p)modp 即可。
算法时间复杂度 O ( log n ) O(\log n) O(logn)
AC Code
C + + \text{C}++ C++
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;typedef long long LL;LL exgcd(LL a, LL b, LL &x, LL &y)
{if (!b){x = 1, y = 0;return a;}LL d = exgcd(b, a % b, y, x);y -= a / b * x;return d;
}int main()
{LL a, b, x, y;cin >> a >> b;exgcd(a, b, x, y);cout << (x % b + b) % b << endl;return 0;
}

最后,如果觉得对您有帮助的话,点个赞再走吧!
相关文章:

AcWing算法提高课-5.6.1同余方程
宣传一下 算法提高课整理 CSDN个人主页:更好的阅读体验 原题链接 题目描述 求关于 x x x 的同余方程 a x ≡ 1 ( m o d b ) ax ≡ 1 \pmod b ax≡1(modb) 的最小正整数解。 输入格式 输入只有一行,包含两个正整数 a , b a,b a,b,用一…...
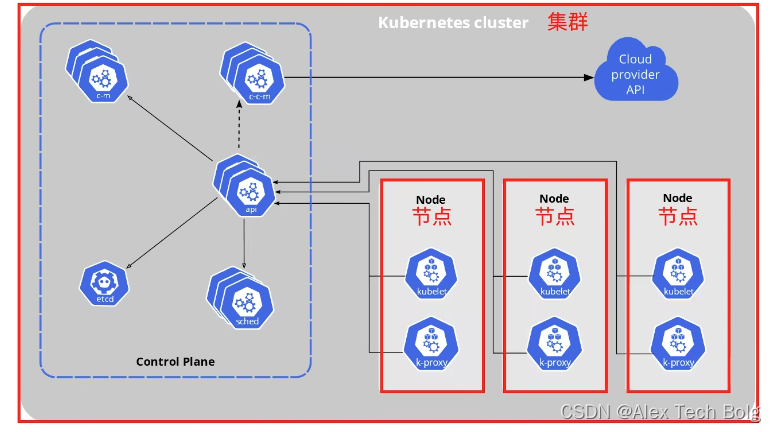
Docker Tutorial
什么是Docker 为每个应用提供完全隔离的运行环境 Dockerfile, Image,Container Image: 相当于虚拟机的快照(snapshot)里面包含了我们需要部署的应用程序以及替它所关联的所有库。通过image,我们可以创建很…...
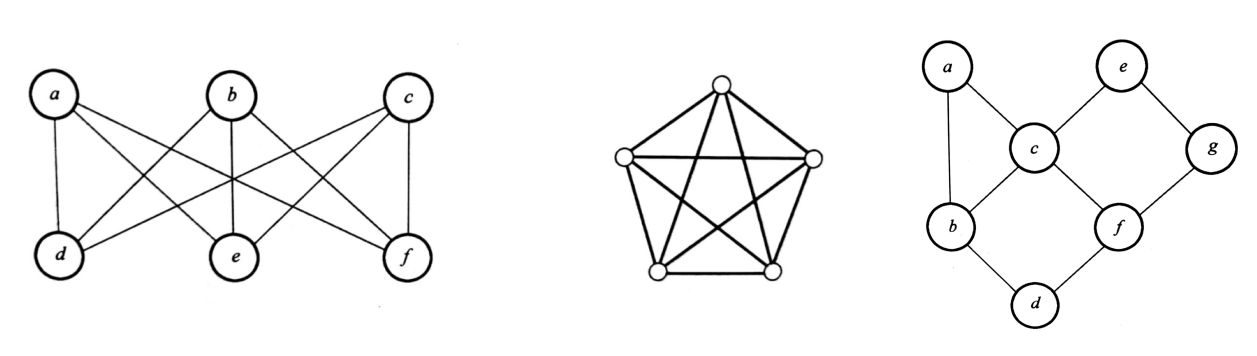
平面图—简单应用
平面图:若一个图𝐺能画在平面𝑆上,且使𝐺的边仅在端点处相交,则称图𝐺为可嵌入平面𝑆,𝐺称为可平面图,简称为平面图。 欧拉公式:设有…...
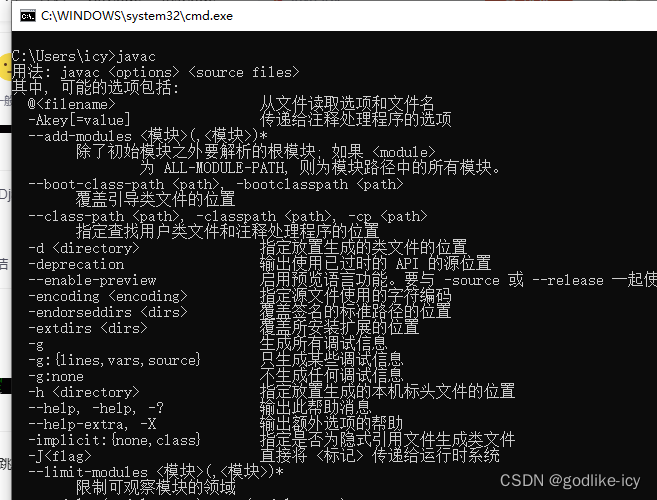
安装JDK(Java SE Development Kit)超详细教程
文章时间 : 2023-10-04 1. 下载地址 直接去下载地址:https://www.oracle.com/java/technologies/downloads/ (需要翻墙,不想翻墙或者不想注册oracel账号的,直接去我的阿里云盘) 阿里云盘:http…...
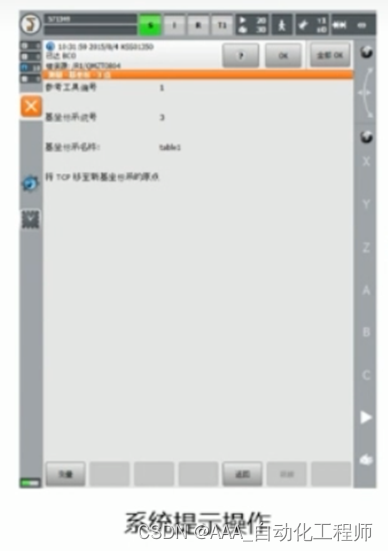
KUKA机器人通过3点法设置工作台基坐标系的具体方法
KUKA机器人通过3点法设置工作台基坐标系的具体方法 具体方法和步骤可参考以下内容: 进入主菜单界面,依次选择“投入运行”—“测量”—基坐标,选择“3点法”, 在系统弹出的基坐标编辑界面,给基座标编号为3,命名为table1,然后单击“继续”按钮,进行下一步操作, 在弹出的…...

以太网的MAC层
以太网的MAC层 一、硬件地址 局域网中,硬件地址又称物理地址或MAC地址(因为用在MAC帧),它是局域网上每一台计算机中固化在适配器的ROM中的地址。 关于地址问题,有这样的定义:“名字指出我们所要寻…...
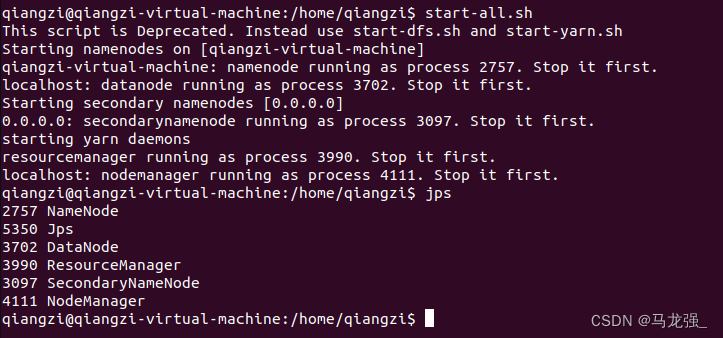
Hadoop启动后jps发现没有DateNode解决办法
多次使用 Hadoop namenode -format 格式化节点后DateNode丢失 找到hadoop配置文件core-site.xml查找tmp路径 进入该路径,使用rm -rf data删除data文件 再次使用Hadoop namenode -format 格式化后jps后出现DateNode节点...
VUE3照本宣科——应用实例API与setup
VUE3照本宣科——应用实例API与setup 前言一、应用实例API1.createApp()2.app.use()3.app.mount() 二、setup 前言 👨💻👨🌾📝记录学习成果,以便温故而知新 “VUE3照本宣科”是指照着中文官网和菜鸟教…...

json/js对象的key有什么区别?
1.对于JS对象来说 一个js对象如果是这样的 obj {"0": "小明","0name": "小明明", "": 18,"¥": "哈哈"," ": "爱好广泛" }对于js对象来说,有时候key是不…...
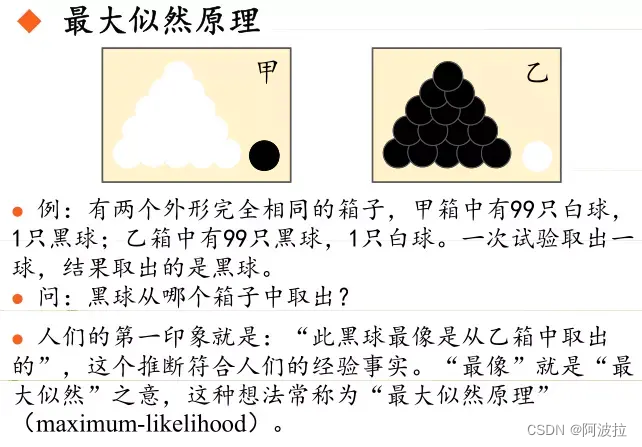
极大似然估计概念的理解——统计学习方法
目录 1.最大似然估计的概念的理解1 2.最大似然估计的概念的理解2 3.最大似然估计的概念的理解3 4.例子 1.最大似然估计的概念的理解1 最大似然估计是一种概率论在统计学上的概念,是参数估计的一种方法。给定观测数据来评估模型参数。也就是模型已知,参…...

python模拟表格任意输入位置
在表格里输入数值,要任意位置,我找到了好方法: input输入 1. 行 2. 列输入:1 excel每行输入文字input输入位置 3.2 表示输入位置在:3行个列是要实现一个类似于 Excel 表格的输入功能,并且希望能够指定输入…...
如何限制文件只能通过USB打印机打印,限制打印次数和时限并且无法在打印前查看或编辑内容
在今天这个高度信息化的时代,文档打印已经成为日常工作中不可或缺的一部分。然而,这也带来了诸多安全风险,如文档被篡改、知识产权被侵犯以及信息泄露等。为了解决这些问题,只印应运而生。作为一款独特的软件工具,只印…...
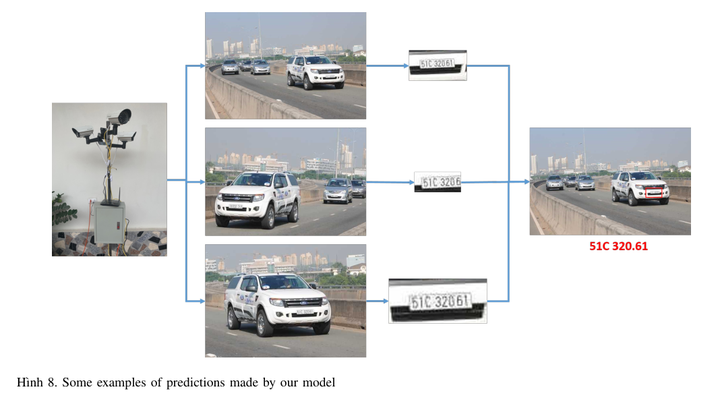
车牌文本检测与识别:License Plate Recognition Based On Multi-Angle View Model
论文作者:Dat Tran-Anh,Khanh Linh Tran,Hoai-Nam Vu 作者单位:Thuyloi University;Posts and Telecommunications Institute of Technology 论文链接:http://arxiv.org/abs/2309.12972v1 内容简介: 1)方向&#x…...

Blender中的4种视图着色模式
Blender中有四种主要的视图着色模式:线框、实体、Look Dev和渲染。它们的主要区别如下: - 线框模式只显示物体的边缘(线框),可以让您看到场景中的所有物体,也可以调整线框的颜色和背景的颜色。 - 实…...
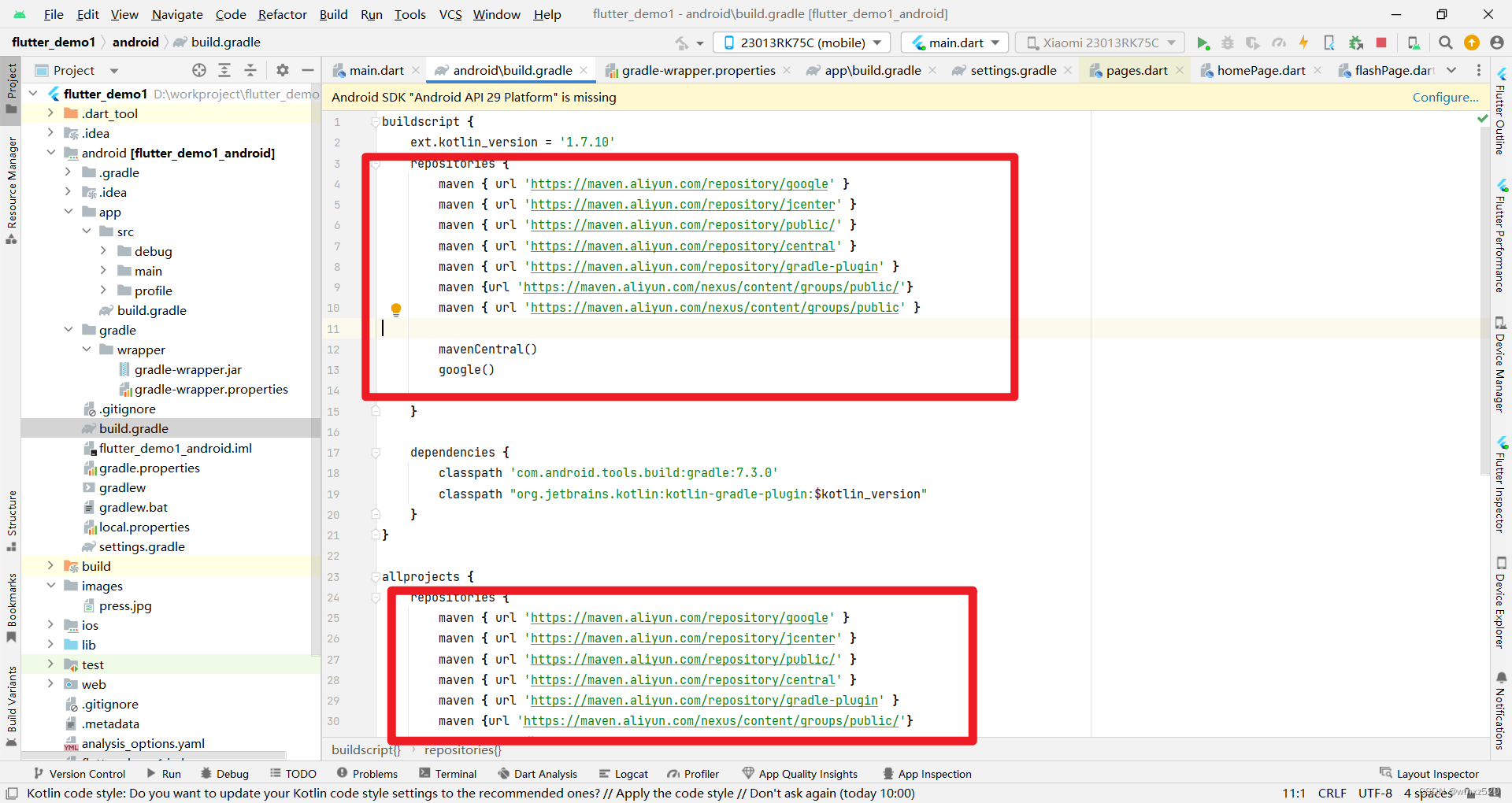
Flutter项目安装到Android手机一直显示在assembledebug
问题 Flutter项目安装到Android手机一直显示在assembledebug 原因 网络不好,gradle依赖下载不下来 解决方案 修改如下的文件 gradle-wrapper.properties 使用腾讯提供的gradle镜像下载 distributionUrlhttps://mirrors.cloud.tencent.com/gradle/gradle-7.5…...
数据预处理【等深分箱与等宽分箱】)
数据挖掘实验(二)数据预处理【等深分箱与等宽分箱】
一、分箱平滑的原理 (1)分箱方法 在分箱前,一定要先排序数据,再将它们分到等深(等宽)的箱中。 常见的有两种分箱方法:等深分箱和等宽分箱。 等深分箱:按记录数进行分箱࿰…...

Vue2 第一次学习
本章为超级浓缩版,文章过于短,方便复习使用哦~ 文章目录 1. 简单引入 vue.js2. 指令2.1 事件绑定指令 v-on (简写 )2.2 内容渲染指令2.3 双向绑定指令 v-model2.4 属性绑定指令 v-bind (简写 : )2.5 条件渲染指令2.6 循环指令 v-for 3. vue 其他知识3.1 侦听器 watch3.2 计算属…...
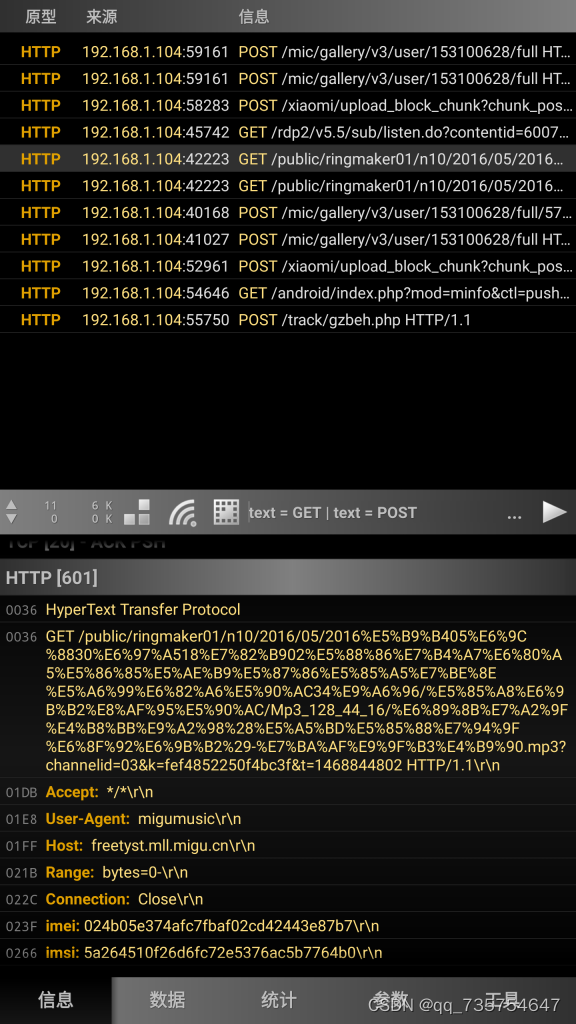
tiny模式基本原理整合
【Tiny模式】的基本构成 M【首头在首位】 U【/】 V【HTTP/】 Host H【真实ip】 XH \r回车 \n换行 \t制表 \ 空格 一个基本的模式构成 [method] [uri] [version]\r\nHost: [host]\r\n[method] [uri] [version]\r\nHost: [host]\r\n 检测顺序 http M H XH 有些地区 XH H M 我这边…...

使用聚氨酯密封件的好处?
聚氨酯密封件因其优异的耐用性、灵活性和广泛的应用范围而在各个行业中广受欢迎。在本文中,我们将探讨使用聚氨酯密封件的优点,阐明其在许多不同领域广泛使用背后的原因。 1、高性能: 聚氨酯密封件具有出色的性能特征,使其成为各…...

DevEco Studio如何安装中文插件
首先 官网下载中文插件 由于DevEco是基于IntelliJ IDEA Community的,所有Compatibility选择“IntelliJ IDEA Community”,然后下载一个对应最新的就ok了。 最后打开Plugins页面,点击右上角齿轮 -> Install Plugin from Disk…。选择下载的…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...
