LeetCode 面试题 08.04. 幂集
文章目录
- 一、题目
- 二、C# 题解
一、题目
幂集。编写一种方法,返回某集合的所有子集。集合中不包含重复的元素。
说明:
- 解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
点击此处跳转题目。
二、C# 题解
记集合为 Q(n),n 为集合中元素个数(不重复)。Sub(i) 表示集合中 i 个元素组成的所有子集,则有如下递推关系:
S u b ( i + 1 ) = S u b ( i ) ∪ S u b ( i ) . A d d ( e l e m ( i + 1 ) ) Sub(i +1)=Sub(i) \cup Sub(i).Add(elem(i+1)) Sub(i+1)=Sub(i)∪Sub(i).Add(elem(i+1))
其中, e l e m ( i + 1 ) elem(i+1) elem(i+1) 表示新增加的第 i + 1 i + 1 i+1 个元素。以集合 { 1 , 2 , 3 } \{1,2,3\} {1,2,3} 为例:
- S u b ( { 0 } ) = { { } } Sub(\{0\})=\{\{\}\} Sub({0})={{}}
- S u b ( { 0 , 1 } ) = { { } } ∪ { { 1 } } = { { } , { 1 } } Sub(\{0,1\})=\{\{\}\}\cup\{\{\bold{1}\}\}=\{\{\},\{1\}\} Sub({0,1})={{}}∪{{1}}={{},{1}}
- S u b ( { 0 , 1 , 2 } ) = { { } , { 1 } } ∪ { { 2 } , { 1 , 2 } } = { { } , { 1 } , { 2 } , { 1 , 2 } } Sub(\{0,1,2\})=\{\{\},\{1\}\}\cup\{\{\bold{2}\},\{1,\bold{2}\}\}=\{\{\},\{1\},\{2\},\{1,2\}\} Sub({0,1,2})={{},{1}}∪{{2},{1,2}}={{},{1},{2},{1,2}}
- S u b ( { 0 , 1 , 2 , 3 } ) = { { } , { 1 } , { 2 } , { 1 , 2 } } ∪ { { 3 } , { 1 , 3 } , { 2 , 3 } , { 1 , 2 , 3 } } = { { } , { 1 } , { 2 } , { 3 } , { 1 , 2 } , { 1 , 3 } , { 2 , 3 } , { 1 , 2 , 3 } } Sub(\{0,1,2,3\})=\{\{\},\{1\},\{2\},\{1,2\}\}\cup\{\{\bold{3}\},\{1,\bold{3}\},\{2,\bold{3}\},\{1,2,\bold{3}\}\}=\{\{\},\{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\},\{1,2,3\}\} Sub({0,1,2,3})={{},{1},{2},{1,2}}∪{{3},{1,3},{2,3},{1,2,3}}={{},{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}
public class Solution {public IList<IList<int>> Subsets(int[] nums) {IList<IList<int>> ans = new List<IList<int>>();ans.Add(new List<int>()); // 添加空集if (nums.Length == 0) return ans;foreach (int t in nums) {int cnt = ans.Count; // 取出原来的长度for (int j = 0; j < cnt; j++) {// 复制原来所有的子集,将新元素添加进去List<int> tmp = new List<int>(ans[j]) { t }; ans.Add(tmp);}}return ans;}
}
- 时间:128 ms,击败 100.00% 使用 C# 的用户
- 内存:40.76 MB,击败 100.00% 使用 C# 的用户
相关文章:

LeetCode 面试题 08.04. 幂集
文章目录 一、题目二、C# 题解 一、题目 幂集。编写一种方法,返回某集合的所有子集。集合中不包含重复的元素。 说明: 解集不能包含重复的子集。 示例: 输入: nums [1,2,3] 输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1…...

【m_listCtrl !=NULL有多个运算符与操作数匹配】2023/9/21 上午11:03:44
2023/9/21 上午11:03:44 m_listCtrl !=NULL有多个运算符与操作数匹配 2023/9/21 上午11:04:00 如果您在编译或运行代码时遇到"M_listCtrl != NULL有多个运算符与操作数匹配"的错误提示,这通常是由于以下几个原因之一: 错误使用运算符:在条件判断语句中,应该使…...

Logrus 集成 color 库实现自定义日志颜色输出字符原理
问题背景 下列代码实现了使用 Logurs 日志框架输出日志时根据级别不同,使用对应的自定义颜色进行输出。那么思考下代码的逻辑是怎么实现的呢? 效果如下: 代码如下: import ("fmt""github.com/sirupsen/logrus&q…...

【Java-LangChain:使用 ChatGPT API 搭建系统-2】语言模型,提问范式与 Token
第二章 语言模型,提问范式与 Token 在本章中,我们将和您分享大型语言模型(LLM)的工作原理、训练方式以及分词器(tokenizer)等细节对 LLM 输出的影响。我们还将介绍 LLM 的提问范式(chat format…...

想要精通算法和SQL的成长之路 - 最长连续序列
想要精通算法和SQL的成长之路 - 最长连续序列 前言一. 最长连续序列1.1 并查集数据结构创建1.2 find 查找1.3 union 合并操作1.4 最终代码 前言 想要精通算法和SQL的成长之路 - 系列导航 并查集的运用 一. 最长连续序列 原题链接 这个题目,如何使用并查集是一个小难…...
- 制图(Draft)-工程图框选制图曲线并输出制图曲线的信息)
UG NX二次开发(C#)- 制图(Draft)-工程图框选制图曲线并输出制图曲线的信息
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1、前言2、在UG NX中打开一个装配体模型3、进入工程制图模块,创建工程制图4、在VS中创建一个工程项目5、在Main()中添加选择的代码(UFun)6、在Main()中添加选择的代码(NXOpen)7、框选解决方案…...

1.7.C++项目:仿muduo库实现并发服务器之Poller模块的设计
项目完整在: 文章目录 一、Poller模块:描述符IO事件监控模块二、提供的功能三、实现思想(一)功能(二)意义(三)功能设计 四、封装思想五、代码(一)框架&#…...

Flutter笔记:build方法、构建上下文BuildContext解析
Flutter笔记 build 方法解析 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/details/133556333 本文主要介绍Flu…...

composer 安装和基本使用
php的包管理软件 如果没有安装php,参考这篇:添加链接描述 1.composer安装 composer官网 需要先安装好php,同时php -v输出有信息 cd /usr/localphp -r "copy(https://install.phpcomposer.com/installer, composer-setup.php);"…...

Ubuntu配置深度学习环境(TensorFlow和PyTorch)
文章目录 一、CUDA安装1.1 安装显卡驱动1.2 CUDA安装1.3 安装cuDNN 二、Anaconda安装三、安装TensorFlow和pyTorch3.1 安装pyTorch3.2 安装TensorFlow2 四、安装pyCharm4.1 pyCharm的安装4.2 关联anaconda的Python解释器 五、VScode配置anaconda的Python虚拟环境 前言ÿ…...

【产品经理】国内企业服务SAAS平台的生存与发展
SaaS在国外发展的比较成熟,甚至已经成为了主流,但在国内这几年才掀起热潮;企业服务SaaS平台在少部分行业发展较快,大部分行业在国内还处于起步、探索阶段;SaaS将如何再国内生存和发展? 在企业服务行业做了五…...

【vue 首屏加载优化】
Vue 首屏加载优化指的是通过一系列的技术手段,尽可能地缩短首屏(即页面中可见的部分)的加载时间,提高用户体验。 以下是一些常见的 Vue 首屏加载优化技巧: 使用 Vue SSR(服务端渲染)࿱…...

docker--redis容器部署及与SpringBoot整合-I
文章目录 1. 容器化部署docker2. 如何与SpringBoot集成2.1. 引入依赖2.2. 添加配置信息2.3. 测试类2.4. 内置的Spring Beansredis 主流客户端比较redissonlettucejedis参考1. 容器化部署docker 拉取镜像创建数据目录data 及 配置目录conf创建配置文件redis.conf启动redis容器进…...

力扣 -- 518. 零钱兑换 II(完全背包问题)
解题步骤: 参考代码: 未优化代码: class Solution { public:int change(int amount, vector<int>& coins) {int ncoins.size();//多开一行,多开一列vector<vector<int>> dp(n1,vector<int>(amount1…...
一文搞懂UART通信协议
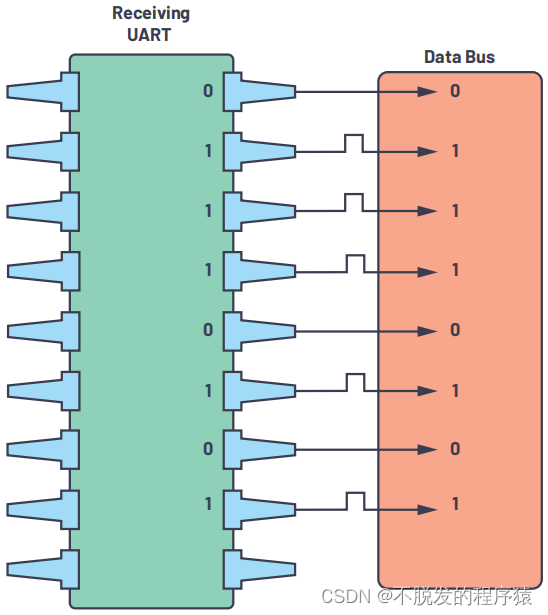
目录 1、UART简介 2、UART特性 3、UART协议帧 3.1、起始位 3.2、数据位 3.3、奇偶校验位 3.4、停止位 4、UART通信步骤 1、UART简介 UART(Universal Asynchronous Receiver/Transmitter,通用异步收发器)是一种双向、串行、异步的通信…...
【算法|动态规划No.7】leetcode300. 最长递增子序列
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【手撕算法系列专栏】【LeetCode】 🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望…...

LeetCode 54 螺旋矩阵
先贴代码 class Solution {public int[][] generateMatrix(int n) {int left 0;int right n-1;int up 0;int down n-1;int[][] result new int[n][n];int number 0;while(left < right && up < down) {for(int ileft;i<right;i) {number;result[up]…...

OpenCV 概念、整体架构、各模块主要功能
文章目录 1. OpenCV 概念2 OpenCV主要模块3 各模块 详细介绍3.1 calib3d 标定3.2 core 核心功能模块3.4 features2d 二维特征3.5 flann 快速近似近邻算法库3.7 highgui 高级图形用户界面3.9 imgproc 图像处理模块3.10 ml 机器学习模块3.11 objdetect 目标检测模块3.12 photo 数…...

组合数与莫队——组合数前缀和
用莫队求组合数是一种常见套路 莫队求 S ( n , m ) ∑ i 0 m ( n i ) S(n,m)\sum_{i0}^m\binom n i S(n,m)∑i0m(in) S ( n , m 1 ) S(n,m1) S(n,m1) 直接做个差,然后就相当于加上 ( n i 1 ) \binom n {i1} (i1n) 求 S ( n 1 , m ) S(n1,m) S(n1,m)…...
stm32之雨滴传感器使用记录
一、简介 雨滴传感器、烟雾传感器(MQ2)、轨迹传感器、干黄管等的原理都类似,都是将检测到的信号通过LM393进行处理之后再输出,可以输出数字信号DO(0和1)和模拟信号A0。 雨滴传感器在正常情况下是AO输出的是…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...

React、Git、计网、发展趋势等内容——前端面试宝典(字节、小红书和美团)
React React Hook实现架构、.Hook不能在循环嵌套语句中使用 , 为什么,Fiber架构,面试向面试官介绍,详细解释 用户: React Hook实现架构、.Hook不能在循环嵌套语句中使用 , 为什么,Fiber架构,面试向面试官介绍&#x…...
shellcode混淆uuid/ipv6/mac)
【免杀】C2免杀技术(十五)shellcode混淆uuid/ipv6/mac
针对 shellcode 混淆(Shellcode Obfuscation) 的实战手段还有很多,如下表所示: 类型举例目的编码 / 加密XOR、AES、RC4、Base64、Poly1305、UUID、IP/MAC改变字节特征,避开静态签名或 YARA结构伪装PE Stub、GIF/PNG 嵌入、RTF OLE、UUID、IP/MAC看起来像合法文件/数据,弱…...
