二叉树的经典OJ题
对称二叉树
- 1.题目
- 2.图形分析
- 3.代码实现
1.题目

2.图形分析



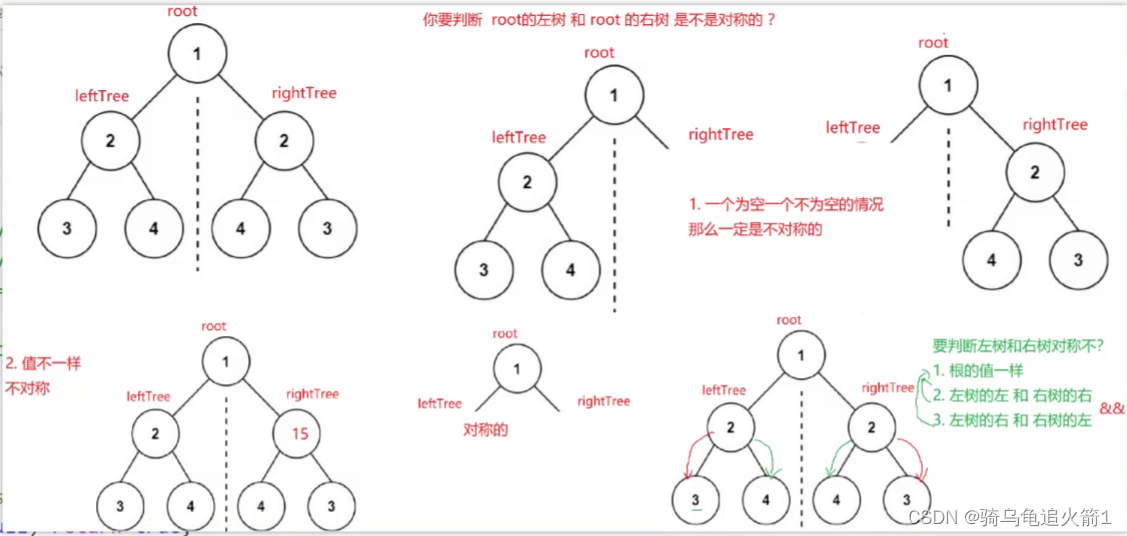
3.代码实现
class Solution {public boolean isSymmetric(TreeNode root) {if(root == null){return true;}return isSymmetricchild(root.left,root.right);}private boolean isSymmetricchild(TreeNode leftTree,TreeNode rightTree){//如果一棵树为空,一棵树不为空的情况if(leftTree == null && rightTree != null || leftTree != null&& rightTree == null){return false;}//两棵树都为空的情况if(leftTree == null && rightTree == null){return true;}//两棵树都不为空的情况下,比较它们的值if(leftTree.val != rightTree.val){return false;}//如果想是对称二叉树 那么必须左子树的左边等于右子树的右边,右子树的左边等于左子树的右边return isSymmetricchild(leftTree.left,rightTree.right)&& isSymmetricchild(leftTree.right,rightTree.left);}
}
相关文章:

二叉树的经典OJ题
对称二叉树 1.题目2.图形分析3.代码实现 1.题目 2.图形分析 3.代码实现 class Solution {public boolean isSymmetric(TreeNode root) {if(root null){return true;}return isSymmetricchild(root.left,root.right);}private boolean isSymmetricchild(TreeNode leftTree,Tre…...
)
统一建模语言UML(1~8章在线测试参考答案)
目录 UML概述 UML概念模型 参与者和用例 用例图之间的关系 用例模型 类图中的类 类图建模 顺序图的构成 UML概述 一 单项选择题(3分) 1、关于UML描述不正确的是()。(1分) UML是由信息系统和面向对象领域三位专家Grady Booch、James Rumbaugh和Ivar Jac…...
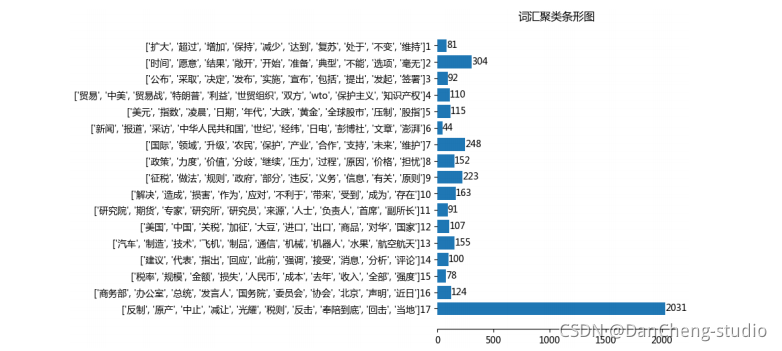
计算机竞赛 题目:基于FP-Growth的新闻挖掘算法系统的设计与实现
文章目录 0 前言1 项目背景2 算法架构3 FP-Growth算法原理3.1 FP树3.2 算法过程3.3 算法实现3.3.1 构建FP树 3.4 从FP树中挖掘频繁项集 4 系统设计展示5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 基于FP-Growth的新闻挖掘算法系统的设计与实现…...

String 类型的变量和常量做 “+” 运算时发生了什么?
先看看字符串不加 final 关键字拼接的情况(jdk1.8): String str1 "str" String str2 "ing" String str3 "str" "ing" String str4 str1 str2 String str5 "string" System.out.println(str3 …...

【Java互联网技术】MinIO分布式文件存储服务
应用场景 互联网海量非结构化数据的存储 基本概念 Object:存储的基本对象,如文件、字节流等 Bucket:存储Object的逻辑空间,相当于顶层文件夹 Drive:存储数据的磁盘,在MinIO启动时,以参数的…...
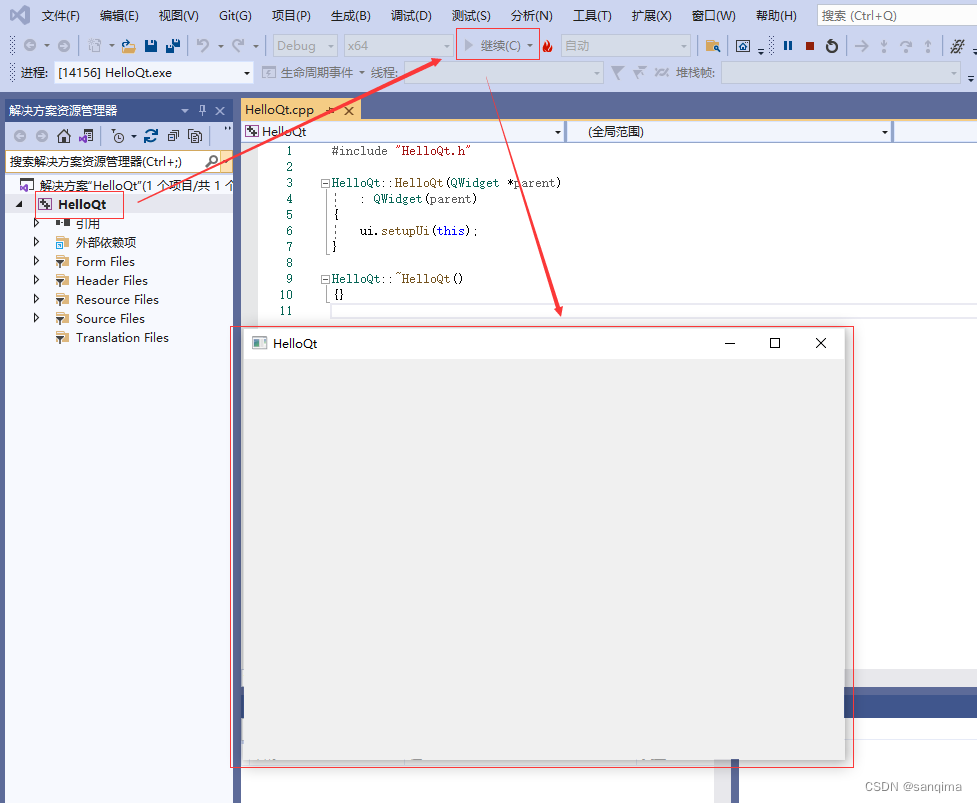
在visual studio里配置Qt插件并运行Qt工程
Qt插件,也叫qt-vsaddin,它以*.vsix后缀名结尾。visual studio简称为VS,从visual studio 2010版本开始,VS支持Qt框架的开发,Qt以插件方式集成到VS里。这里简述在visual studio 2019里配置Qt 5.14.2插件,并配…...

【C语言】利用数组处理批量数据(字符数组)
前言:前面已经介绍了,字符数据是以字符的ASCII代码存储在存储单元中的,一般占一个字节。由于ASCII代码也属于整数形式,因此在C99标准中,把字符类型归纳为整型类型中的一种。 💖 博主CSDN主页:卫卫卫的个人主页 &#x…...

算法通过村第十二关-字符串|白银笔记|经典面试题
文章目录 前言1. 反转问题1.1 反转字符串1.2 k个一组反转1.3 仅仅反转字母1.3.1 采用栈实现操作1.3.2 采用双指针实现操作 1.4 反转字符串里面的单词1.4.1 使用语言提供的方法来解决(内置API)1.4.2 如何优雅自己实现上述功能 2. 验证回文串3. 字符串中的第一个唯一字符4. 判断是…...
《视觉 SLAM 十四讲》V2 第 5 讲 相机与图像
文章目录 相机 内参 && 外参5.1.2 畸变模型单目相机的成像过程5.1.3 双目相机模型5.1.4 RGB-D 相机模型 实践5.3.1 OpenCV 基础操作 【Code】OpenCV版本查看 5.3.2 图像去畸变 【Code】5.4.1 双目视觉 视差图 点云 【Code】5.4.2 RGB-D 点云 拼合成 地图【Code】 习题题…...
)
使用libmodbus库开发modbusTcp从站(支持多个主站连接)
使用libmodbus库开发modbusTcp从站(支持多个主站连接) Chapter1 使用libmodbus库开发modbusTcp从站(支持多个主站连接)rdsmodbusslave.hrdsmodbusslave.cppmain.cpp Chapter1 使用libmodbus库开发modbusTcp从站(支持多个主站连接) 参考链接:…...
GPT系列论文解读:GPT-2
GPT系列 GPT(Generative Pre-trained Transformer)是一系列基于Transformer架构的预训练语言模型,由OpenAI开发。以下是GPT系列的主要模型: GPT:GPT-1是于2018年发布的第一个版本,它使用了12个Transformer…...
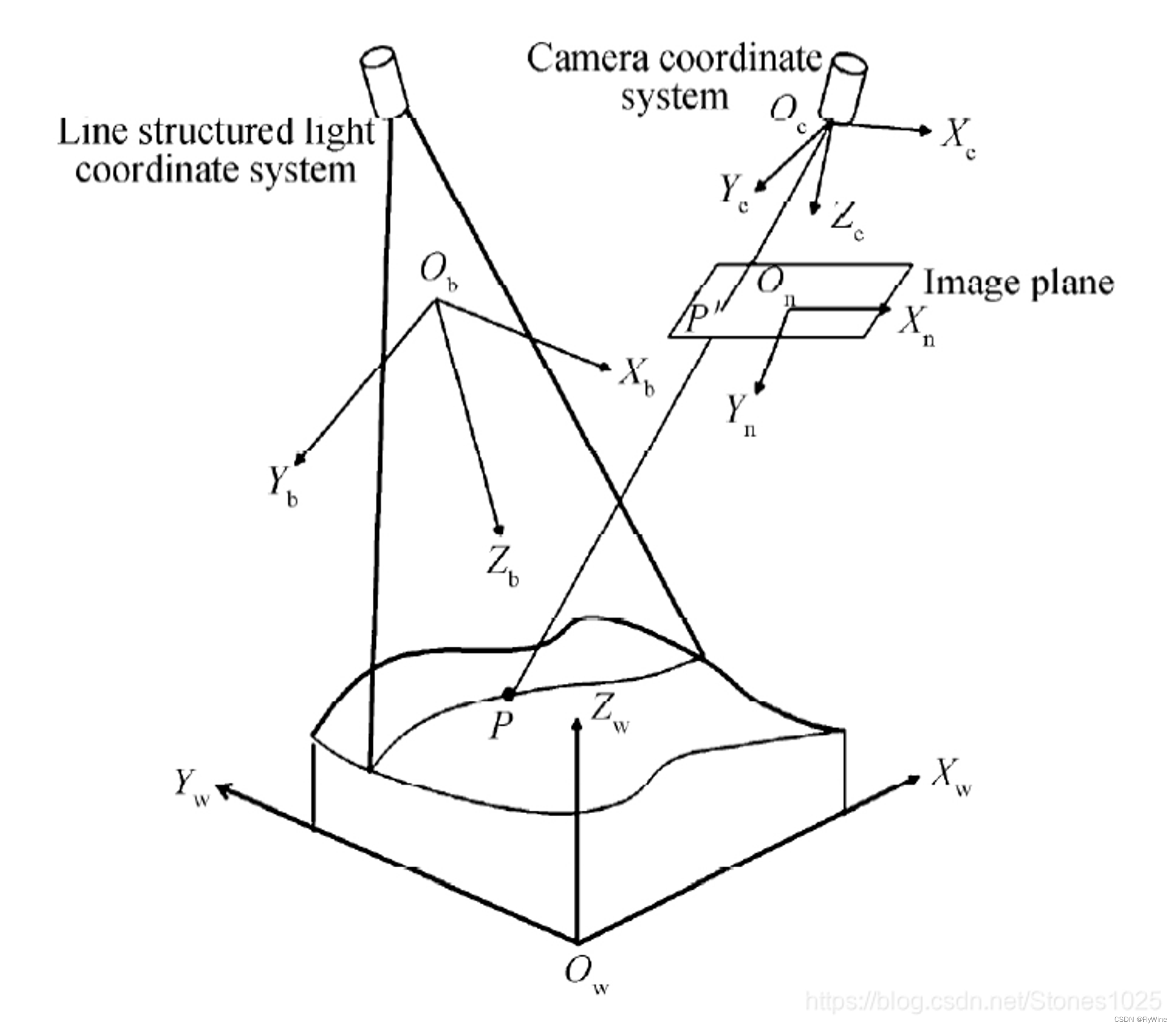
(四)激光线扫描-光平面标定
在上一章节,已经实现了对激光线条的中心线提取,并且在最开始已经实现了对相机的标定,那么相机标定的作用是什么呢? 就是将图像二维点和空间三维点之间进行互相转换。 1. 什么是光平面 激光发射器投射出一条线,形成的一个扇形区域平面就是光平面,也叫光刀面,与物体相交…...
妙不可言的Python之旅----(二)
Python基础语法 什么是字面量 字面量:在代码中,被写下来的的固定的值,称之为字面量 常用的值类型 类型 描述 说明 数字(Number) 支持 • 整数(int) • 浮点数(floatÿ…...

cartographer(1)-运行
1.下载数据集 #1.下载数据集: mkdir /home/tang/bagfiles#2.开始二维建图 cd /home/tang/carto_ws/cartographer_detailed_comments_ws/install_isolated/source install_isolated/setup.bash rospack profile #新装的包索引地址存在ros的环境里 roslaunch ca…...

C++:模板进阶与继承
模板进阶与继承 模板进阶1.非类型的模板参数2.模板的特化2.1特化的概念2.2函数模板特化2.3类模板特化2.4全特化和偏特化2.4.1全特化2.4.2偏特化 3.模板的分离编译3.1同文件分离3.2不同文件下分离 继承1.继承的概念和定义1.1继承的概念1.2继承的定义1.2.1定义格式1.2.2继承关系和…...

vue-img-cutter 实现图片裁剪[vue 组件库]
借助 vue-img-cutter 可以在网页端实现图片裁剪功能,最终功能效果如下: 组件 npm 安装 npm install vue-img-cutter2 --save-dev # for vue2 npm install vue-img-cutter3 --save-dev # for vue3vue-img-cutter使用 template模板标签模块,…...

手把手教你从零开始腾讯云服务器部署(连接建站教程)
使用腾讯云服务器搭建网站全流程,包括轻量应用服务器和云服务器CVM建站教程,轻量可以使用应用镜像一键建站,云服务器CVM可以通过安装宝塔面板的方式来搭建网站,腾讯云服务器网txyfwq.com分享使用腾讯云服务器建站教程,…...
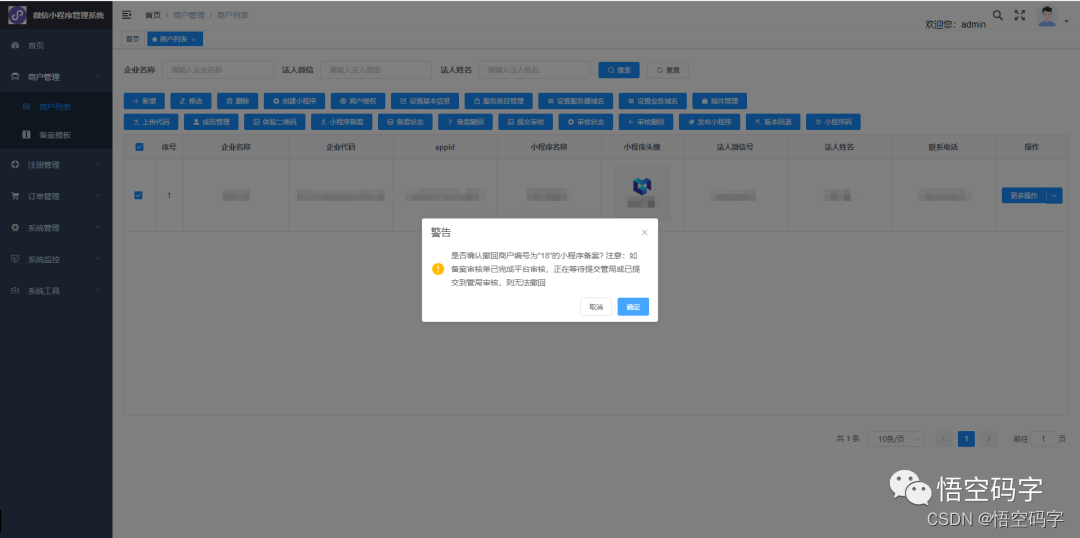
微信开放平台第三方开发,实现代小程序备案申请
大家好,我是小悟 微信小程序备案整体流程总共分为五个环节:备案信息填写、平台初审、工信部短信核验、通管局审核和备案成功。 服务商可以代小程序发起备案申请。在申请小程序备案之前,需要确保小程序基本信息已填写完成、小程序至少存在一个…...

设计模式——11. 享元模式
1. 说明 享元模式(Flyweight Pattern)是一种结构型设计模式,它旨在减少系统中相似对象的内存占用或计算开销,通过共享相同的对象来达到节省资源的目的。 享元模式的核心思想是将对象的状态分为内部状态(Intrinsic State)和外部状态(Extrinsic State): 内部状态是对象…...

【LLM】主流大模型体验(文心一言 科大讯飞 字节豆包 百川 阿里通义千问 商汤商量)
note 智谱AI体验百度文心一言体验科大讯飞大模型体验字节豆包百川智能大模型阿里通义千问商汤商量简要分析:仅从测试“老婆饼为啥没有老婆”这个问题的结果来看,chatglm分点作答有条理(但第三点略有逻辑问题);字节豆包…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
