【蓝桥集训】第七天——并查集
作者:指针不指南吗
专栏:Acwing 蓝桥集训每日一题🐾或许会很慢,但是不可以停下来🐾
文章目录
- 1.亲戚
- 2.合并集合
- 3.连通块中点的数量
有关并查集的知识学习可以移步至—— 【算法】——并查集
1.亲戚
或许你并不知道,你的某个朋友是你的亲戚。
他可能是你的曾祖父的外公的女婿的外甥女的表姐的孙子。
如果能得到完整的家谱,判断两个人是否是亲戚应该是可行的,但如果两个人的最近公共祖先与他们相隔好几代,使得家谱十分庞大,那么检验亲戚关系实非人力所能及。
在这种情况下,最好的帮手就是计算机。
为了将问题简化,你将得到一些亲戚关系的信息,如Marry和Tom是亲戚,Tom和Ben是亲戚,等等。
从这些信息中,你可以推出Marry和Ben是亲戚。
请写一个程序,对于我们的关于亲戚关系的提问,以最快的速度给出答案。
输入格式
输入由两部分组成。
第一部分以 N,M开始。N 为问题涉及的人的个数。这些人的编号为 1,2,3,…,N。下面有 M 行,每行有两个数 ai,bia_i,b_iai,bi ,表示已知 aia_iai 和 bib_ibi 是亲戚。
第二部分以 Q 开始。以下 Q 行有 Q 个询问,每行为 ci,dic_i,d_ici,di ,表示询问 cic_ici 和 did_idi 是否为亲戚。
输出格式
对于每个询问ci,dic_i,d_ici,di ,输出一行:若 cic_ici 和 did_idi 为亲戚,则输出“Yes”,否则输出“No”。
数据范围
1≤N≤20000,
1≤M≤10610^6106 ,
1≤Q≤10610^6106 .输入样例:
10 7 2 4 5 7 1 3 8 9 1 2 5 6 2 3 3 3 4 7 10 8 9输出样例:
Yes No Yes
-
思路
- 把每个家族看成一个集合:人之间互为亲戚,则说明他们是一个家族的,用一个编号来表示;
- 这个题比较简单,就是并查集的两个朴素操作:
- 两个人互为亲戚,进行家族合并,即并查集合并
- 查询两个人是否为亲戚,即看看这两人的家族是否一样
-
代码实现
#include<bits/stdc++.h> using namespace std;const int N=200010;int n,m; //n表示人数,m表示操作的次数 int p[N];int find(int x) //找到家族编号,即根节点 {if(p[x]!=x) p[x]=find(p[x]);return p[x]; }int main() {scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) p[i]=i; //初始化父节点while(m--){ //m次合并操作,亲戚互认int a,b;scanf("%d%d",&a,&b);if(find(a)!=find(b)) p[find(a)]=find(b); //家族集合合并}int q;cin>>q;while(q--){ //q次查询,是否是亲戚,一个家族集合的int x,y;scanf("%d%d",&x,&y);if(find(x)==find(y)) puts("Yes"); else puts("No");}return 0; }
2.合并集合
一共有 n 个数,编号是 1∼n,最开始每个数各自在一个集合中。
现在要进行 m 个操作,操作共有两种:
M a b,将编号为 a 和 b 的两个数所在的集合合并,如果两个数已经在同一个集合中,则忽略这个操作;Q a b,询问编号为 a 和 b 的两个数是否在同一个集合中;输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为
M a b或Q a b中的一种。输出格式
对于每个询问指令
Q a b,都要输出一个结果,如果 a 和 b 在同一集合内,则输出Yes,否则输出No。每个结果占一行。
数据范围
1≤n,m≤10510^5105
输入样例:
4 5 M 1 2 M 3 4 Q 1 2 Q 1 3 Q 3 4输出样例:
Yes No Yes
-
代码实现
#include<bits/stdc++.h> using namespace std;const int N=100010;int n,m; //n表示点的数量,m表示操作的次数 int p[N]; //存的每个节点的父节点int find(int x) //返回x的祖宗节点+路径压缩 {if(p[x]!=x) p[x]=find(p[x]);return p[x]; }int main() {scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) p[i]=i; //最开始,每个点都各自在一个集合中,so父节点就是他本身;while(m--){char op[2];int a,b;scanf("%s%d %d",op,&a,&b);//合并if(op[0]=='M') p[find(a)]=p[find(b)]; //让a的祖宗节点等于b的祖宗节点,让a的祖宗节点直接插在b祖宗节点下面else{if(find(a)==find(b)) puts("Yes"); //判断是否属于同一个集合else puts("No");} }return 0; }
注意
读入字母M或者是Q的时候,使用字符串op[2],是因为直接用char的话,可能会出现空格换行的问题作物,这种比较保险,记得在后面使用的时候,用op[0],不能直接使用op
puts自动包含换行
3.连通块中点的数量
给定一个包含 n 个点(编号为 1∼n)的无向图,初始时图中没有边。
现在要进行 m 个操作,操作共有三种:
C a b,在点 a 和点 b 之间连一条边,a 和 b 可能相等;Q1 a b,询问点 a 和点 b 是否在同一个连通块中,a 和 b 可能相等;Q2 a,询问点 a 所在连通块中点的数量;输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为
C a b,Q1 a b或Q2 a中的一种。输出格式
对于每个询问指令
Q1 a b,如果 a 和 b 在同一个连通块中,则输出Yes,否则输出No。对于每个询问指令
Q2 a,输出一个整数表示点 a 所在连通块中点的数量每个结果占一行。
数据范围
1≤n,m≤10510^5105
输入样例:
5 5 C 1 2 Q1 1 2 Q2 1 C 2 5 Q2 5输出样例:
Yes 2 3
-
思路
-
连通块就是一个点的集合:集合中的点可以相互到达,直接或者是间接都是可以的;
-
这时候我们可以把它类比成一个树,运用并查集,一个点集合,我们可以用一个编号来表示,属于同一个编号,就说明两个点之间可以相互到达,在一个连通块里面;
-
有三个操作:
-
两点之间连一条边,那么这两个点所在集合中的点,都是可以相互到达的,即合成一个连通块,用并查集中的合并操作;
-
判断是否在一个连通块,用并查集的查询;
-
询问一个点集合的数量,需要我们额外维护,初始化的时候每个集合1个,合并的时候,两个集合数量相加,最后输出即可
-
-
-
代码实现
#include<bits/stdc++.h>using namespace std;const int N=1000010; int n,m; int p[N],sizel[N]; //p表示父节点,sizel表示集合的大小,记住sizel里面放的是祖宗节点,后面容易出错int find(int n) //返回祖宗节点 {if(p[n]!=n) p[n]=find(p[n]);return p[n]; }int main() {scanf("%d%d",&n,&m); //读入点的数量和操作的次数for(int i=1;i<=n;i++){ //初始化,父节点就是它本身;集合大小都是1,只有他自己p[i]=i;sizel[i]=1;}char op[5]; while(m--){scanf("%s",op); //读入操作的名字if(op[0]=='C'){ //合并int a,b;scanf("%d%d",&a,&b);if(find(a)==find(b)) continue; //相同则进入下个循环else{ //不同即操作,两步的顺序不能反!!!sizel[find(b)]+=sizel[find(a)]; //b的集合大小加上a的集合大小p[find(a)]=find(b); //让a的祖宗节点指向b的祖宗节点}}else if(op[1]=='1'){ //查询是否一个集合int a,b;scanf("%d%d",&a,&b);if(find(a)==find(b)) puts("Yes");else puts("No");}else{if(op[1]=='2') { //输出集合大小int d;scanf("%d",&d);printf("%d\n",sizel[find(d)]); }}}return 0; }

相关文章:

【蓝桥集训】第七天——并查集
作者:指针不指南吗 专栏:Acwing 蓝桥集训每日一题 🐾或许会很慢,但是不可以停下来🐾 文章目录1.亲戚2.合并集合3.连通块中点的数量有关并查集的知识学习可以移步至—— 【算法】——并查集1.亲戚 或许你并不知道&#…...

该来的总会来,继岳云鹏走红之后,孔云龙也和主流相声界打成一片
说起德云社的岳云鹏,都知道他是农民的孩子,初中没有毕业就外出打工,一路辛酸才走到了今天。当年岳云鹏在北京打工,炸酱面馆里面他和孔云龙最好,两个人又经过老先生介绍,一起投奔郭德纲学说相声。 进入德云社…...

索引的创建与设计原则
1.索引的声明与使用 1.1索引的分类 MySQL的索引包括普通索引、唯一性索引、全文索引、单列索引、多列索引和空间索引等。 从 功能逻辑 上说,索引主要有 4 种,分别是普通索引、唯一索引、主键索引、全文索引。按照 物理实现方式,索引可以分…...

day51【代码随想录】动态规划之回文子串、最长回文子序列
文章目录前言一、回文子串(力扣647)二、最长回文子序列(力扣516)前言 1、回文子串 2、最长回文子序列 一、回文子串(力扣647) 给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目…...
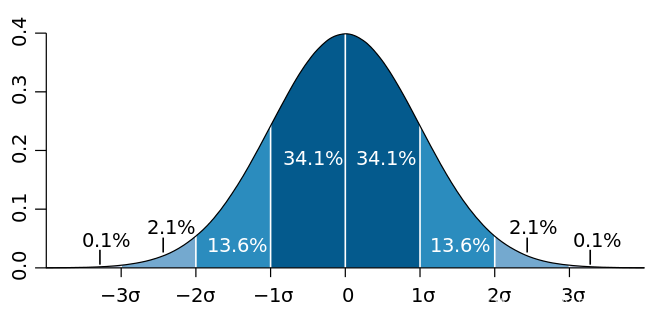
拟凸函数,拟凹函数,单峰函数
拟凸(quasi-convex)函数很早就听说过,但是标准定义一直不太了解,现在总结一下。 一个定义在凸集上的实数函数 fff 是拟凸函数:若对于其定义域内的任意两个点 xxx 和 yyy,以及任意常数 λ∈[0,1]\lambda\in…...
代码:卡尔曼滤波 vs. 卡尔曼平滑)
数据处理(伪)代码:卡尔曼滤波 vs. 卡尔曼平滑
步骤一、导入csv或txt格式的试验数据 最简洁也是据说读取速度最快的方法是: pPath C:\data_org\9#-1.txt % 数据文件 data importdata(pPath); % 读取 pPath 的结果到 一个数据结构变量 data 中。 pData data.data; % 提取有效数据数组data 的数据结构如下&a…...

华为OD机试题,用 Java 解【比赛评分】问题
最近更新的博客 华为OD机试 - 猴子爬山 | 机试题算法思路 【2023】华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】华为OD机试 - 非严格递增连续数字序列 | 机试题算法思路 【2023】华为OD机试 - 消消乐游戏(Java) | 机试题算法思路 【2023】华为OD机试 - 组成最大数…...

【基础算法】哈希表(开放寻址法)
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...
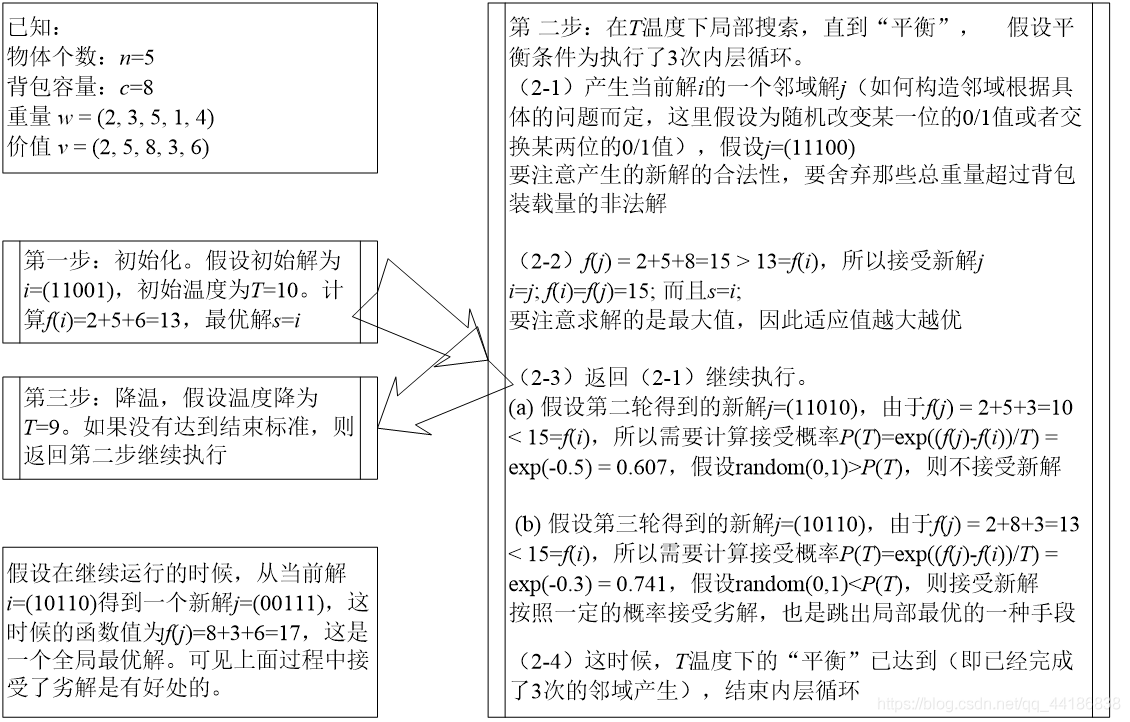
优化算法(寻优问题)
前言 群智能算法(全局最优):模拟退火算法(Simulated annealing,SA),遗传算法(Genetic Algorithm, GA),粒子群算法(Particle Swarm Optimization&…...

基于视频流⽔线的Opencv缺陷检测项⽬
代码链接见文末 1.数据与任务概述 输入为视频数据,我们需要从视频中检测出缺陷,并对缺陷进行分类。 2.整体流程 (1)视频数据读取和轮廓检测 首先,我们需要使用opencv读取视频数据,将彩色图转为灰度图后进行图像阈值处理。阈值处理是为了让前景和背景更明显的区分处理。…...
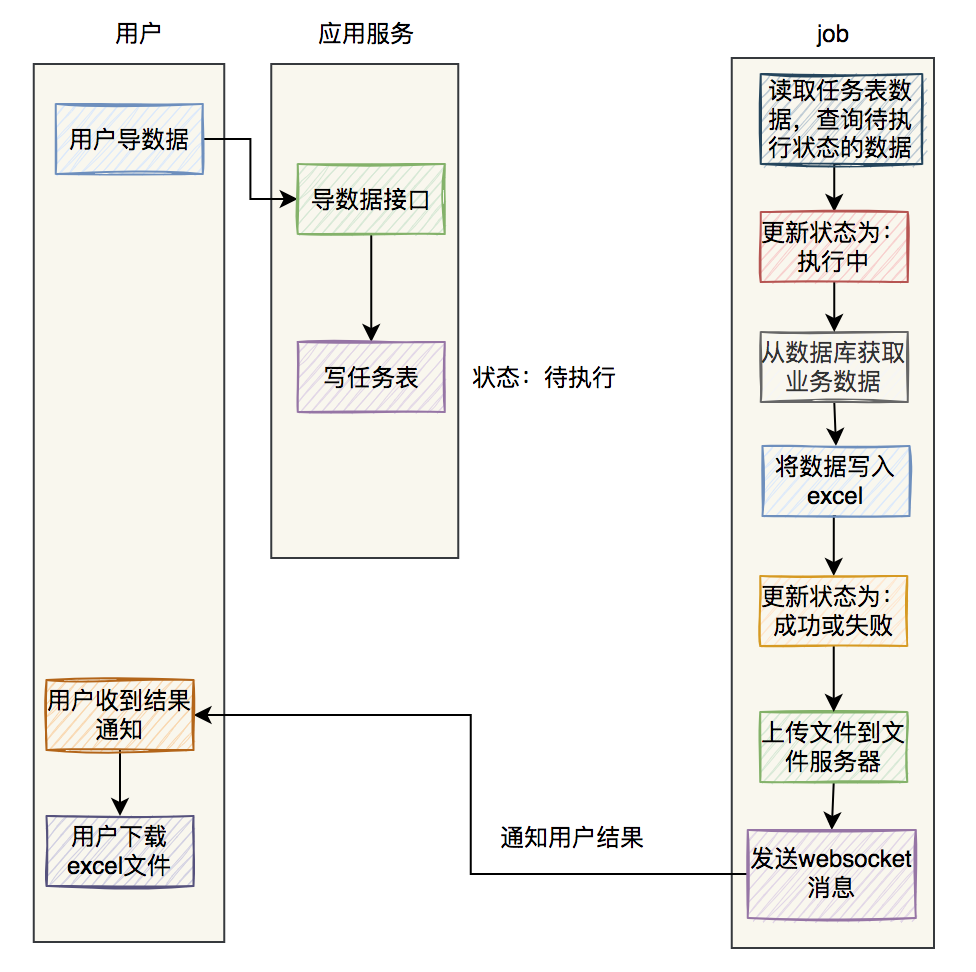
百万数据excel导出功能如何实现?
最近我做过一个MySQL百万级别数据的excel导出功能,已经正常上线使用了。 这个功能挺有意思的,里面需要注意的细节还真不少,现在拿出来跟大家分享一下,希望对你会有所帮助。 原始需求:用户在UI界面上点击全部导出按钮…...

华为OD机试题,用 Java 解【合规数组】问题
最近更新的博客 华为OD机试 - 猴子爬山 | 机试题算法思路 【2023】华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】华为OD机试 - 非严格递增连续数字序列 | 机试题算法思路 【2023】华为OD机试 - 消消乐游戏(Java) | 机试题算法思路 【2023】华为OD机试 - 组成最大数…...
SAP ABAP中的数据类型 Data Types
简单来说分两种: 数据字典里定义的在ABAP程序里定义的 文章目录1. ABAP数据字典里的1.1 数字型的1.2 字符型1.3 字节型1.4 特殊类型2. 预定义的ABAP数据类型2.1 预定义数字型2.2 预定义字符型2.3 预定义字节型1. ABAP数据字典里的 1.1 数字型的 用在数学计算里的…...
HashMap~
HashMap: HashMap是面试中经常被问到的一个内容,以下两个经常被问到的问题, Question1:底层数据结构,1.7和1.8有何不同? 答:1.7数组+链表,1.8数组+(链表|红…...
EasyNLP集成K-Global Pointer算法,支持中文信息抽取
作者:周纪咏、汪诚愚、严俊冰、黄俊 导读 信息抽取的三大任务是命名实体识别、关系抽取、事件抽取。命名实体识别是指识别文本中具有特定意义的实体,包括人名、地名、机构名、专有名词等;关系抽取是指识别文本中实体之间的关系;…...

mysql lesson3
DQL查找语句续集.............................. 分组函数(也叫多行处理函数) 1: select sum(sal) from emp;select min(sal)from emp;select max(sal)from emp;select avg(sal)from emp;select count(ename)from emp;2:分组函…...
python源码保护
文章目录代码混淆打包exe编译为字节码源码加密项目发布部署时,为防止python源码泄漏,可以通过几种方式进行处理代码混淆 修改函数、变量名 打包exe 通过pyinstaller 将项目打包为exe可执行程序,不过容易被反编译。 编译为字节码 py_comp…...

第51讲:SQL优化之COUNT查询的优化
文章目录 1.COUNT查询优化的概念2.COUNT函数的用法1.COUNT查询优化的概念 在很多的业务场景下可能需要统计一张表中的总数据量,当表的数据量很大时,使用COUNT统计表数据量时,也是非常耗时的。 MyISAM引擎会把一个表的总行记录在磁盘中,当执行count(*)的时候会直接从磁盘中…...

ArrayBlockingQueue
同步队列超出长度时,不同的返回形式可以分为以下四种。 会抛异常不会抛异常,有返回值死等,直到可以插入值或者取到值设置等待超时时间添加方法add()offfer()put()offer(E e,long timeout, TimeUnit unit)删除方法remove()poll()take()poll(l…...

DeepLabV3+:对预测处理的详解
相信大家对于这一部分才是最感兴趣的,能够实实在在的看到效果。这里我们就只需要两个.py文件(deeplab.py、predict_img.py)。 创建DeeplabV3类 deeplab.py的作用是为了创建一个DeeplabV3类,提供一个检测图片的方法,而…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
