【布隆过滤器(Bloom Filter)基本概念与原理、Bloom Filter优点与缺点、以及应用场景】
布隆过滤器(Bloom Filter)基本概念与原理、Bloom Filter优点与缺点、以及应用场景

Bloom Filter 基本概念
布隆过滤器是1970年由一个叫布隆的小伙子提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。
Bloom Filter 原理
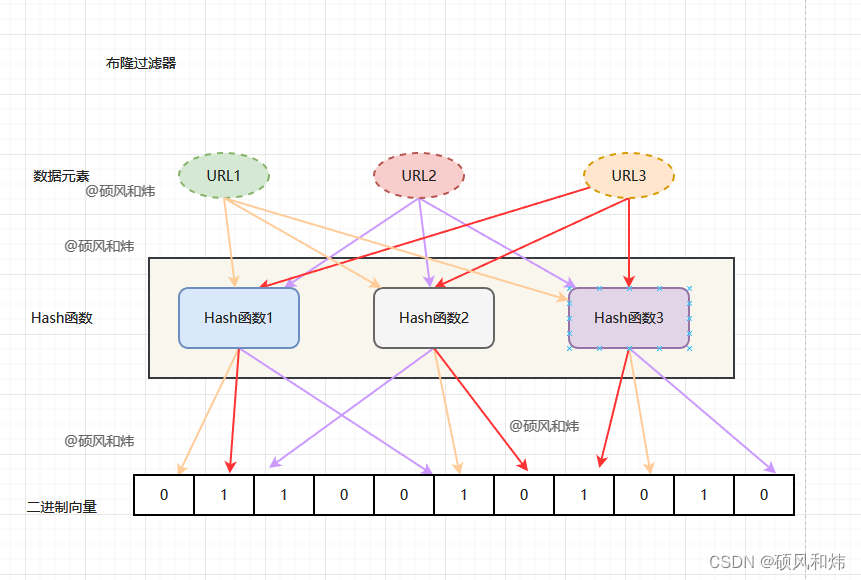
布隆过滤器的原理是,当一个元素被加入集合时,通过K个散列函数将这个元素映射成一个位数组中的K个点,把它们置为1。检索时,我们只要看看这些点是不是都是1就(大约)知道集合中有没有它了:如果这些点有任何一个0,则被检元素一定不在;如果都是1,则被检元素很可能在。这就是布隆过滤器的基本思想。
那么就会有人问了,Bloom Filter和Bit-Map有什么不同呢?
Bloom Filter使用了k个哈希函数,每个字符串跟k个bit对应。从而降低了冲突的概率。如下图所示:
Bloom Filter优点与缺点
世界上没有完美的人或者事,技术也一样,Bloom Filter可以快速的找到某一个数是否存在并且能很好的帮我们解决缓存穿透的问题,但是带来的问题就是牺牲了判断的准确率、删除的便利性。
优点
它的优点是空间效率和查询时间都远远超过一般的算法。
缺点:
- 存在误判,可能要查到的元素并没有在容器中,但是hash之后得到的k个位置上值都是1。如果bloom filter中存储的是黑名单,那么可以通过建立一个白名单来存储可能会误判的元素。
- 删除困难。一个放入容器的元素映射到bit数组的k个位置上是1,删除的时候不能简单的直接置为0,可能会影响其他元素的判断。
Bloom Filter 应用场景
- 解决缓存穿透问题,快速的判断某一个数是否存在
- 垃圾邮件地址过滤
- 爬虫URL地址去重
- Google著名的分布式数据库Bigtable以及Hbase使用了布隆过滤器来查找不存在的行或列,以及减少磁盘查找的IO次数
- 文档存储检查系统也采用布隆过滤器来检测先前存储的数据
- Goole Chrome浏览器使用了布隆过滤器加速安全浏览服务
总结
关于布隆过滤器基本概念与原理、Bloom Filter优点与缺点、以及应用场景就先介绍到这里,当然关于布隆过滤器相关的知识还有很多内容并没有讲到,这个就需要你先看懂这些,然后再一步深入学习。如果对你有帮助,就留下你的小关注吧!
相关文章:

【布隆过滤器(Bloom Filter)基本概念与原理、Bloom Filter优点与缺点、以及应用场景】
布隆过滤器(Bloom Filter)基本概念与原理、Bloom Filter优点与缺点、以及应用场景 Bloom Filter 基本概念 布隆过滤器是1970年由一个叫布隆的小伙子提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在…...

unity的Rendertexture上面显示粒子特效最便捷的解决方案
一、为什么不显示 1.为什么粒子特效也不显示? 不显示是正常的,因为当前为背景的点设置为A为0时已经被剔除,当前位置粒子特效的颜色也会被剔除。 因为clip发生在融合blend之前,blend发生在所有颜色输出之后的帧缓存。 2.为什么NGUI的Unlit/Premultiplied Colored的shade…...

Docker 查询、停止、删除和重启容器
docker 列出所有容器IDdocker ps -aq[rootlocalhost conf]# docker ps -aq f81aa5f48427 06a66409d7ce 1c3d38b948ba 62233dfad35b 4b0032878886 0f6f368c4c1d 7d98a59a8012 1906ba6bfbe1 [rootlocalhost conf]#docker 查看所有运行容器docker ps -a[rootlocalhost conf]# dock…...
)
面试历程(3)
1、HashMap为什么要使用红黑树,不能使用平衡二叉树(AVL树) 二叉查找树具有的特性: 左子树上所有结点的值均小于或等于它的根结点的值。右子树上所有结点的值均大于或等于它的根结点的值。左、右子树也分别为二叉排序树。AVL树是严格平衡二叉树(左右两个子树的高度差的绝对…...
【storybook】你需要一款能在独立环境下开发组件并生成可视化控件文档的框架吗?(二)
storybook回顾继续说说用法配置文件介绍回顾 上篇博客地址: https://blog.csdn.net/tuzi007a/article/details/129192502说了部分用法。 继续说说用法 配置文件介绍 开发环境的配置都在.storybook目录中,里面包含了2个文件 main.js preview.js先看m…...
(免费分享)基于ssm的BBS社区论坛系统带论文
项目描述前台部分:1.用户注册登录模块用户登录后,可以进行发帖回帖功能,在线签到功能,完善个人信息,添加好友,收藏贴子,评论帖子,点赞功能,记录功能(比如记录今天发生的事情)等等…2.排行榜模块1.帖子讨论热度排行,分两种排行方式:(1) 根据用户今日发出的帖子被回复数量进行排名…...
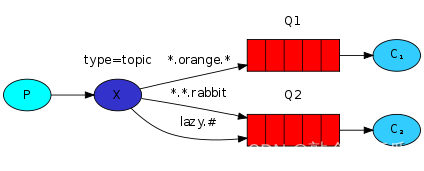
RebbitMQ 消息队列(简单使用)
消息队列介绍 MQ的优势 1.业务解耦:不同系统消费信息互不关联,灵活增减系统数量,修改某个系统其他系统也不影响 2.异步提速:不同系统之间可同时响应,提升并发量 3.削峰填谷:处理消息高峰期,均摊…...

OpenCV-Python学习(21)—— OpenCV 图像几何变换之图像翻转(cv.flip、np.flip)
1. 学习目标 学习 OpenCV 图像的翻转函数 cv.flip;学习 NumPy 矩阵的反转函数 np.flip;自己实现矩阵反转的函数。 2. OpenCV 翻转 翻转也称镜像,是指将图像沿轴线进行轴对称变换。水平镜像是将图像沿垂直中轴线进行左右翻转,垂直…...

CRM系统能帮外贸行业解决哪些问题
国内的外贸行业经历了四个发展阶段,从发展期到繁荣期,CRM客户管理系统逐步走到幕前,成为外贸企业必不可少的主打工具。那么外贸行业整面临哪些问题?该如何解决?下面我们就来说说适合外贸行业的CRM解决方案。 外贸行业…...

掌握lombok简化Java编码完成后端提效
Lombok安装 –>添加依赖 <dependency><groupId>org.projectlombok</groupId><artifactId>lombok</artifactId><version>1.18.16</version><scope>provided</scope> </dependency>scopeprovided,说…...

【蓝桥集训】第七天——并查集
作者:指针不指南吗 专栏:Acwing 蓝桥集训每日一题 🐾或许会很慢,但是不可以停下来🐾 文章目录1.亲戚2.合并集合3.连通块中点的数量有关并查集的知识学习可以移步至—— 【算法】——并查集1.亲戚 或许你并不知道&#…...

该来的总会来,继岳云鹏走红之后,孔云龙也和主流相声界打成一片
说起德云社的岳云鹏,都知道他是农民的孩子,初中没有毕业就外出打工,一路辛酸才走到了今天。当年岳云鹏在北京打工,炸酱面馆里面他和孔云龙最好,两个人又经过老先生介绍,一起投奔郭德纲学说相声。 进入德云社…...

索引的创建与设计原则
1.索引的声明与使用 1.1索引的分类 MySQL的索引包括普通索引、唯一性索引、全文索引、单列索引、多列索引和空间索引等。 从 功能逻辑 上说,索引主要有 4 种,分别是普通索引、唯一索引、主键索引、全文索引。按照 物理实现方式,索引可以分…...

day51【代码随想录】动态规划之回文子串、最长回文子序列
文章目录前言一、回文子串(力扣647)二、最长回文子序列(力扣516)前言 1、回文子串 2、最长回文子序列 一、回文子串(力扣647) 给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目…...
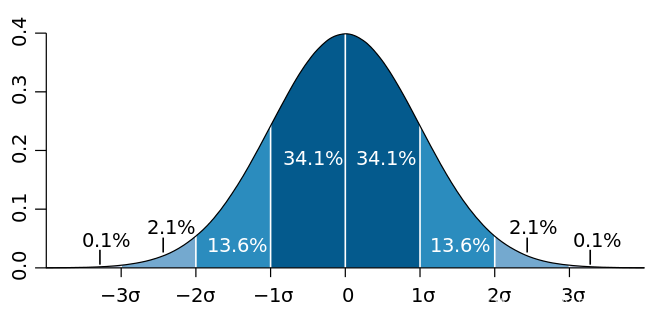
拟凸函数,拟凹函数,单峰函数
拟凸(quasi-convex)函数很早就听说过,但是标准定义一直不太了解,现在总结一下。 一个定义在凸集上的实数函数 fff 是拟凸函数:若对于其定义域内的任意两个点 xxx 和 yyy,以及任意常数 λ∈[0,1]\lambda\in…...
代码:卡尔曼滤波 vs. 卡尔曼平滑)
数据处理(伪)代码:卡尔曼滤波 vs. 卡尔曼平滑
步骤一、导入csv或txt格式的试验数据 最简洁也是据说读取速度最快的方法是: pPath C:\data_org\9#-1.txt % 数据文件 data importdata(pPath); % 读取 pPath 的结果到 一个数据结构变量 data 中。 pData data.data; % 提取有效数据数组data 的数据结构如下&a…...

华为OD机试题,用 Java 解【比赛评分】问题
最近更新的博客 华为OD机试 - 猴子爬山 | 机试题算法思路 【2023】华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】华为OD机试 - 非严格递增连续数字序列 | 机试题算法思路 【2023】华为OD机试 - 消消乐游戏(Java) | 机试题算法思路 【2023】华为OD机试 - 组成最大数…...

【基础算法】哈希表(开放寻址法)
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...
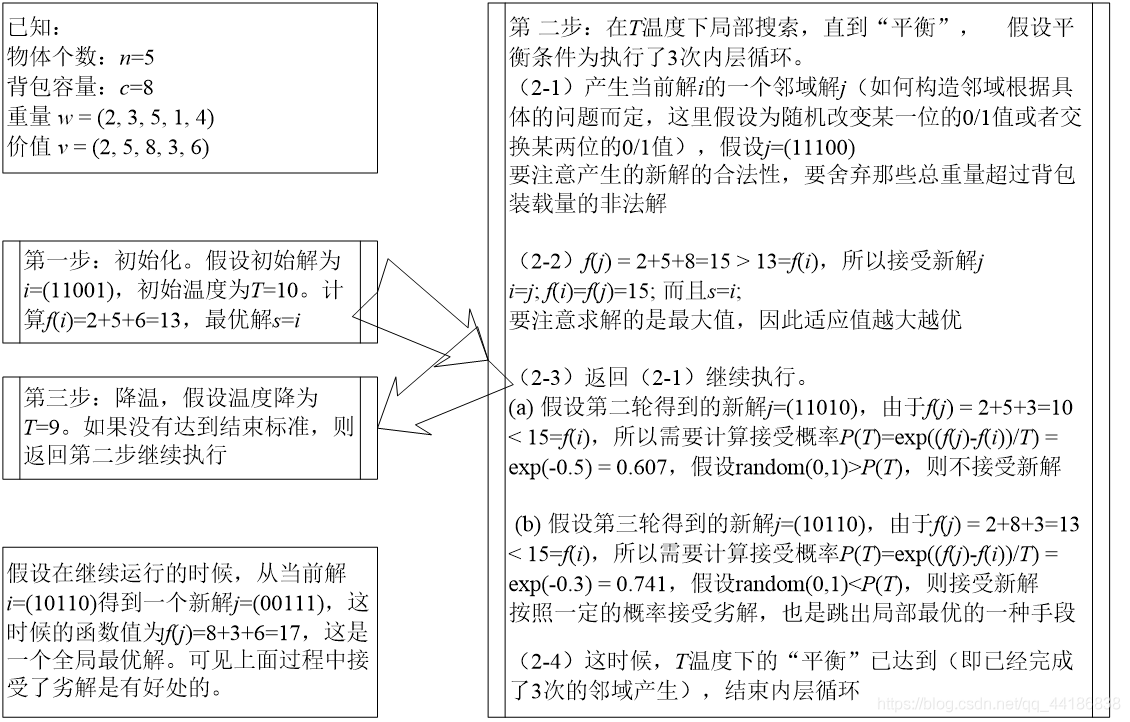
优化算法(寻优问题)
前言 群智能算法(全局最优):模拟退火算法(Simulated annealing,SA),遗传算法(Genetic Algorithm, GA),粒子群算法(Particle Swarm Optimization&…...

基于视频流⽔线的Opencv缺陷检测项⽬
代码链接见文末 1.数据与任务概述 输入为视频数据,我们需要从视频中检测出缺陷,并对缺陷进行分类。 2.整体流程 (1)视频数据读取和轮廓检测 首先,我们需要使用opencv读取视频数据,将彩色图转为灰度图后进行图像阈值处理。阈值处理是为了让前景和背景更明显的区分处理。…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
