【数据结构】红黑树
红黑树
- 一、红黑树的概念
- 二、红黑树的接口
- 2.1 插入
- 三、验证
- 四、源码
一、红黑树的概念
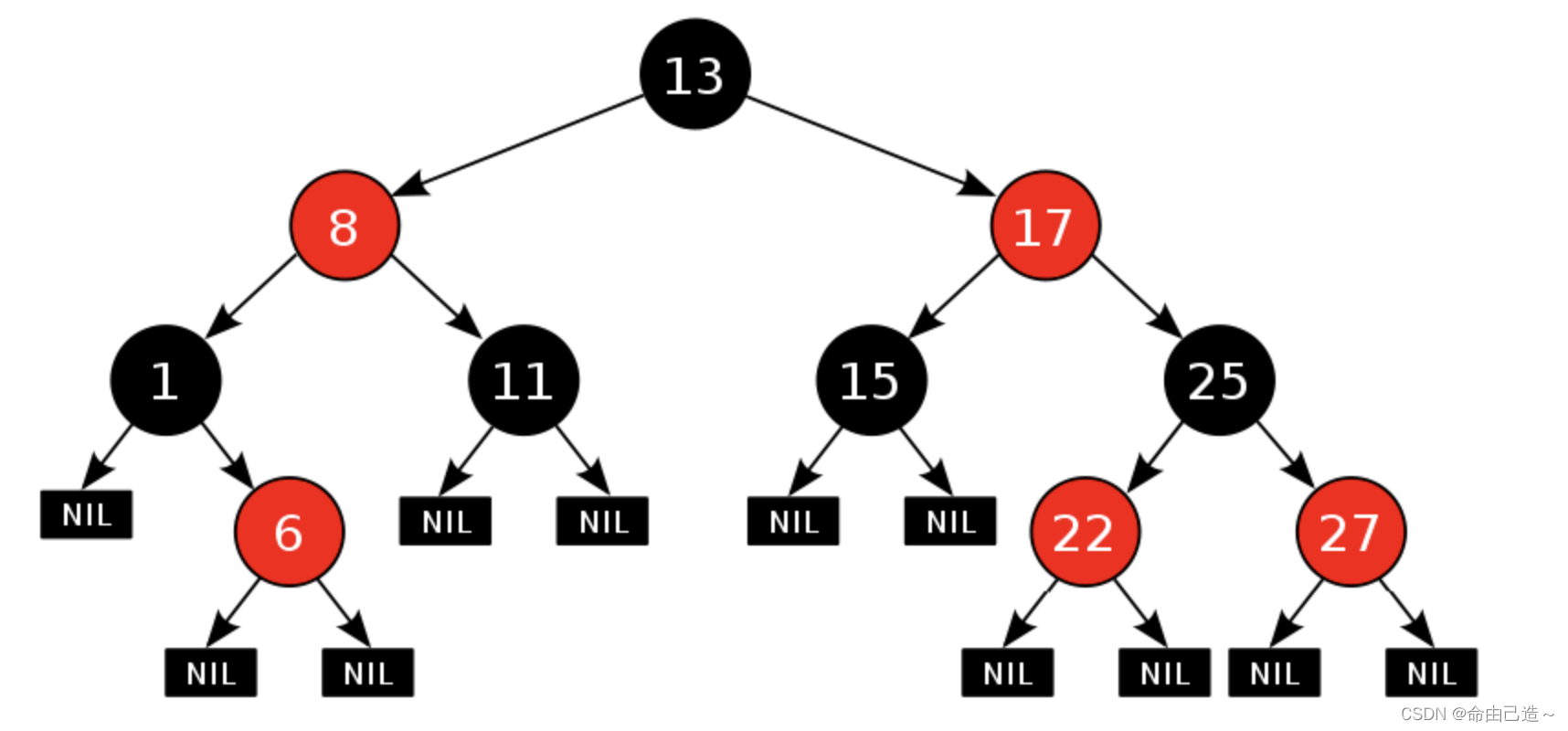
红黑树也是一个二叉搜索树,他是通过对任何一条从根到叶子的路径上各个结点着色方式的限制,最长路径长度不超过最短路径长度的 2 倍保持近似平衡。他在每个节点添加了一个变量用来表示颜色 :Black或者Red,为了满足上面的条件,着色必须满足性质:
1️⃣每个结点不是红色就是黑色
2️⃣ 根节点是黑色的
3️⃣ 如果一个节点是红色的,则它的两个孩子结点是黑色的(没有连续的红色节点)
4️⃣ 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
5️⃣ 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
由此可以满足最长路径长度不超过最短路径长度的 2 倍(通过第四点就可以看出)。
既然不能保证绝对平衡,那么搜索性能肯定不如AVL树,那么为什么还要有红黑树呢?
首先要知道AVL树保持平衡的方法是频繁的旋转,而红黑树则不需要严格的平衡,会少很多旋转。
二、红黑树的接口
红黑树节点定义:
节点需要有个颜色的变量,可以使用枚举的方法:
enum Colour
{RED,BLACK,
};template <class K, class V>
struct RBTreeNode
{RBTreeNode(const pair<K, V>& kv): _kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}pair<K, V> _kv;AVLNode<K, V>* _left;AVLNode<K, V>* _right;AVLNode<K, V>* _parent;Colour _col;
};
2.1 插入
我们可以看到节点初始化的时候默认为RED,因为如果要插入BLACK,那么一定会导致错误,不满足对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点。
所以只能把新节点默认设置为RED,因为如果是红色有可能父节点是黑色,这样就没有出现连续的红色。
总结一下:
插入黑色节点一定有问题,插入红色节点有可能会出问题。
插入的流程根AVL树一样,检查父亲节点,如果是黑就结束,如果是红就要调整红黑树。
为了方便说明,cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
首先要知道最主要的是看u
情况一:cur为红,p为红,g为黑,u存在且为红 :

为什么要看u节点,因为如果cur为红且p为红,那么g一定为黑。所以唯一的变数就为u
它的调整方法为:
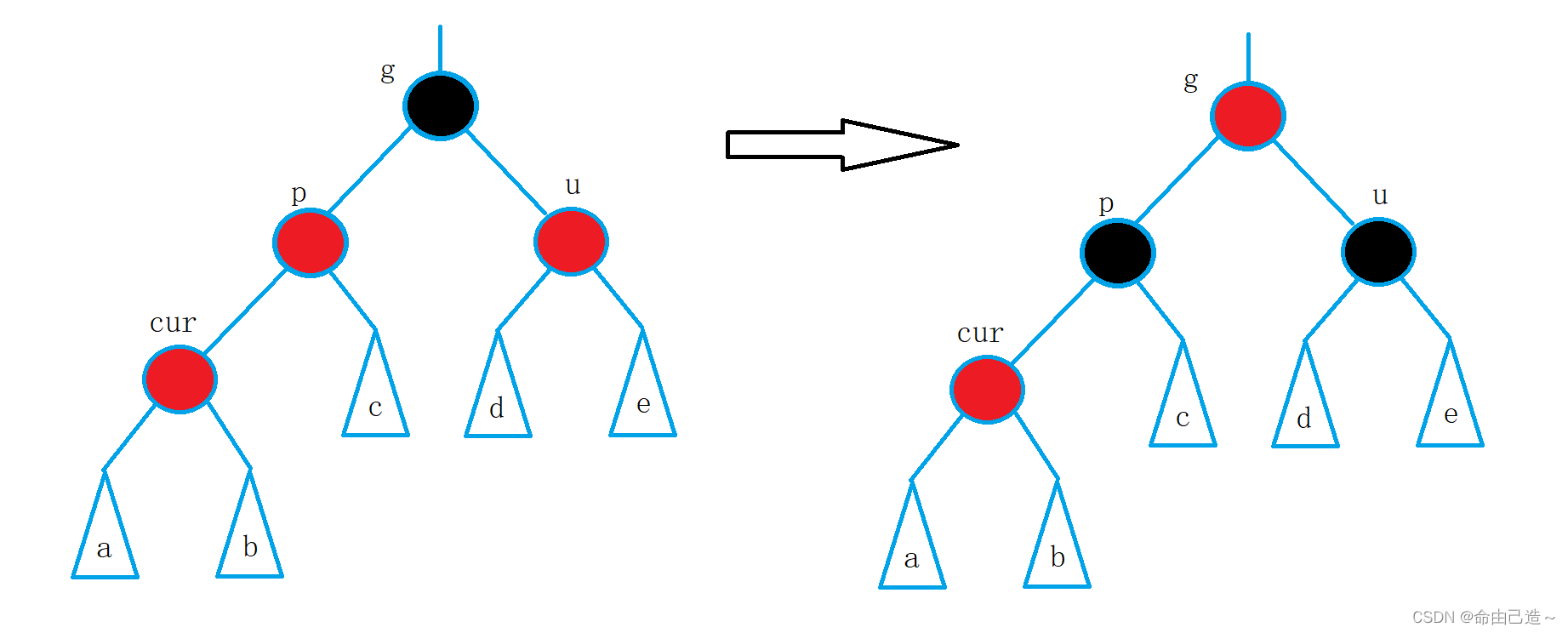
首先p肯定要变黑,而为了使g两边的子树黑节点数目相同,u也要变黑。至于g,我们先把它变红,因为如果这颗树是子树而g还是黑,那么相当于这颗子树的黑节点多了一个,会影响到别的子树。如果g为根那么就把g变为黑。
这里要注意继续往上处理:
把g当成cur,继续向上调整。
举个例子:
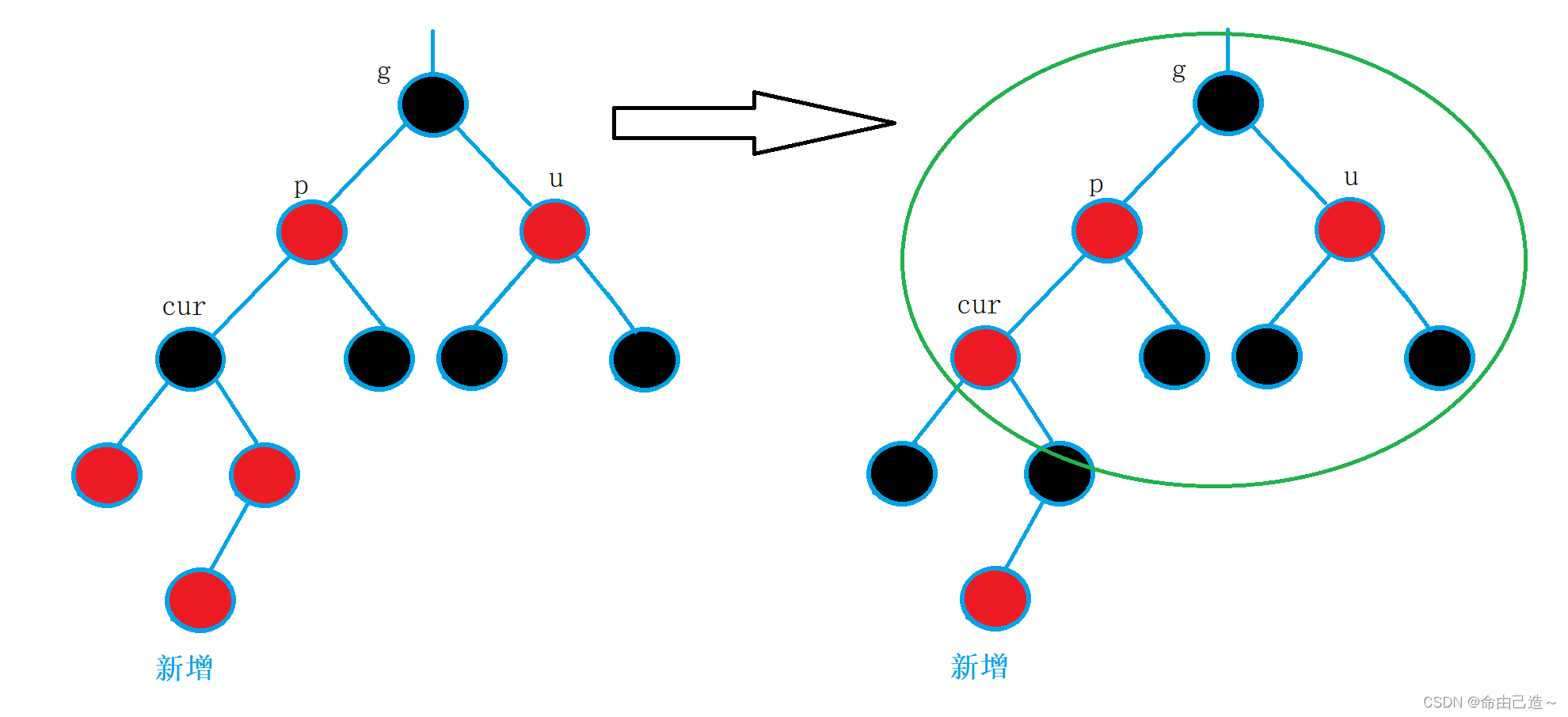
可以看到绿色部分就为上面的抽象图,就这么往上循环改变颜色即可。
情况二:cur为红,p为红,g为黑,u不存在/u为黑

此时要对u分情况讨论:
1️⃣ u不存在时,那么cur一定是新增节点,因为如果cur不是新增节点,那么cur和p一定有一个节点为黑,这样就不满足黑节点数目相同的条件。

处理方式就为右单旋
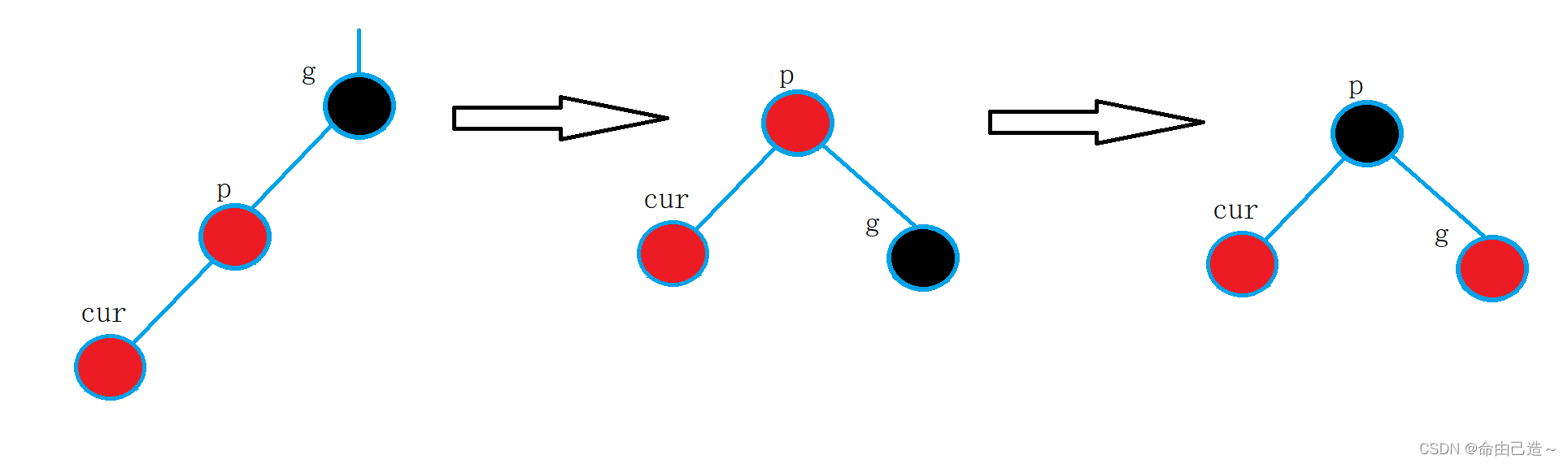
2️⃣ u存在且为黑
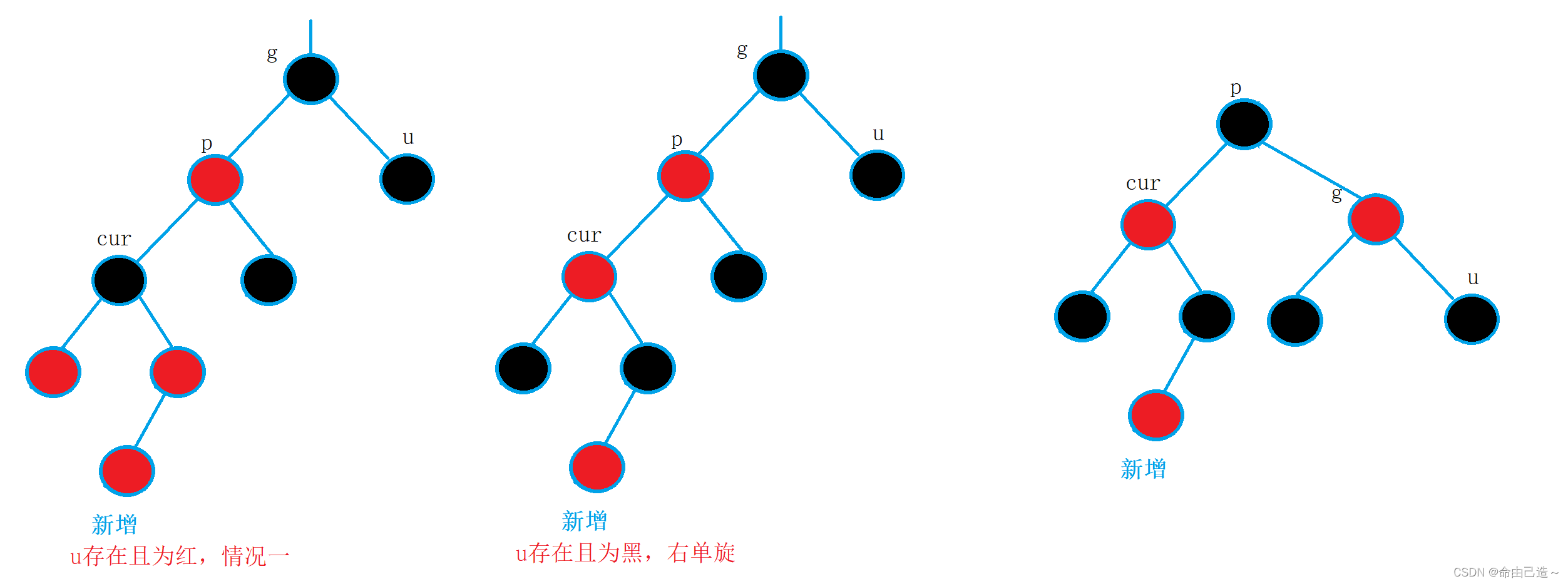
总结一下:
u不存在则cur是新增节点,u存在那么就是由情况一变换过来的。
情况二的处理方法就是旋转+变色。
情况三: cur为红,p为红,g为黑,u不存在/u为黑
情况三与情况二的区别就是情况二是直线,情况三是折线,经过AVL的学习我们知道这种情况要双旋。
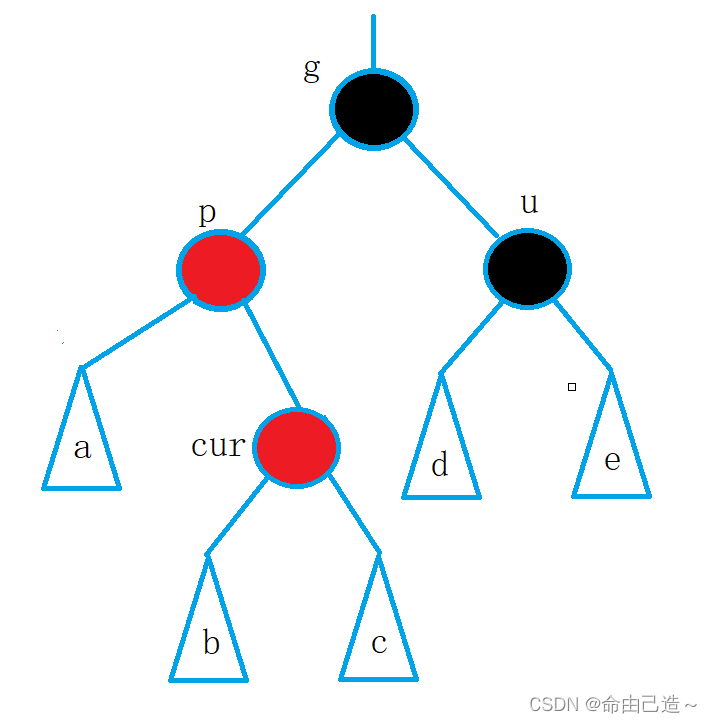
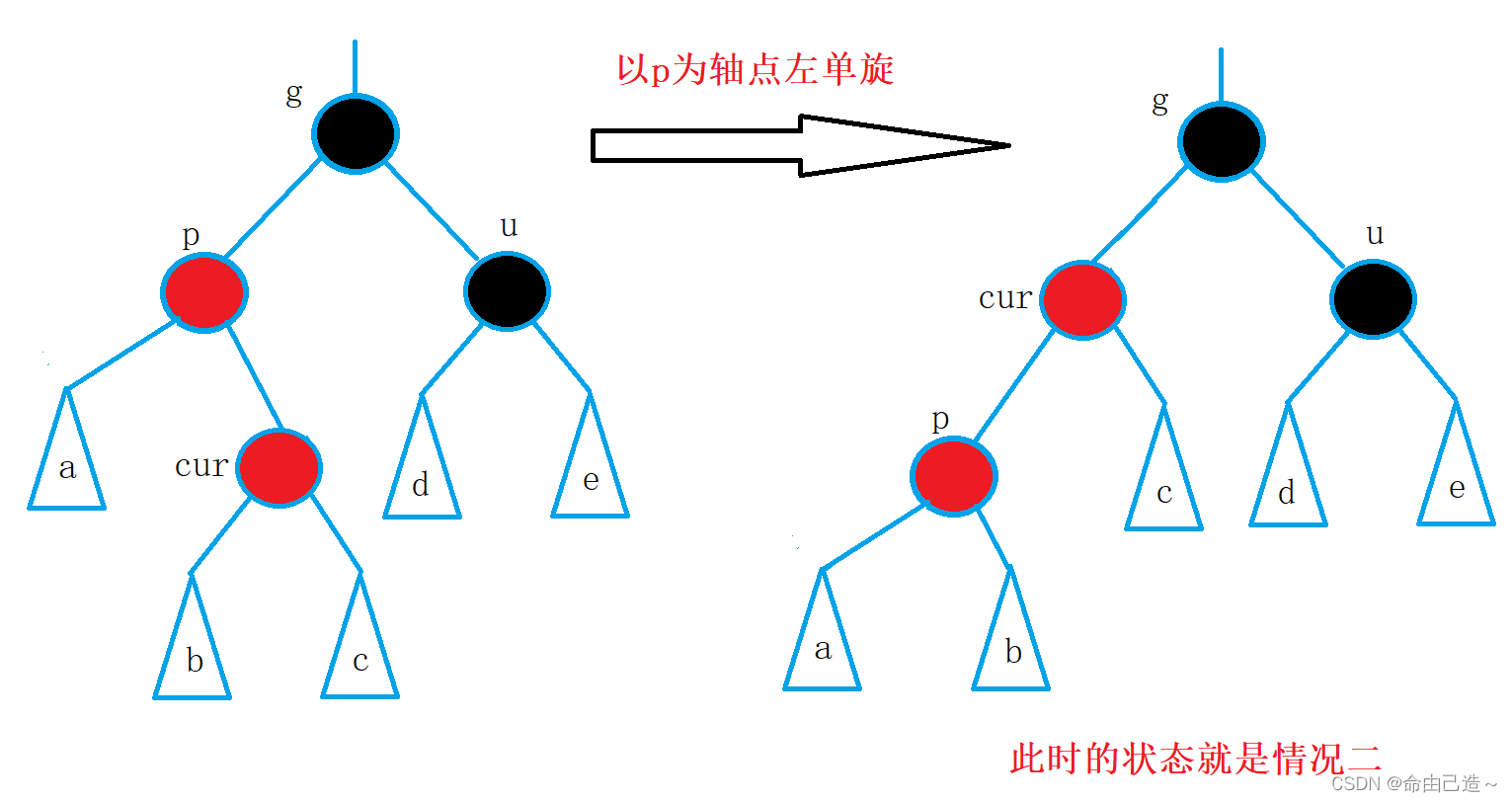
情况三也是由其他情况变过来的。
此时我们就需要进行双旋调整红黑树。
左单旋后变成了情况二,那么按照情况二的方法进行右旋即可。
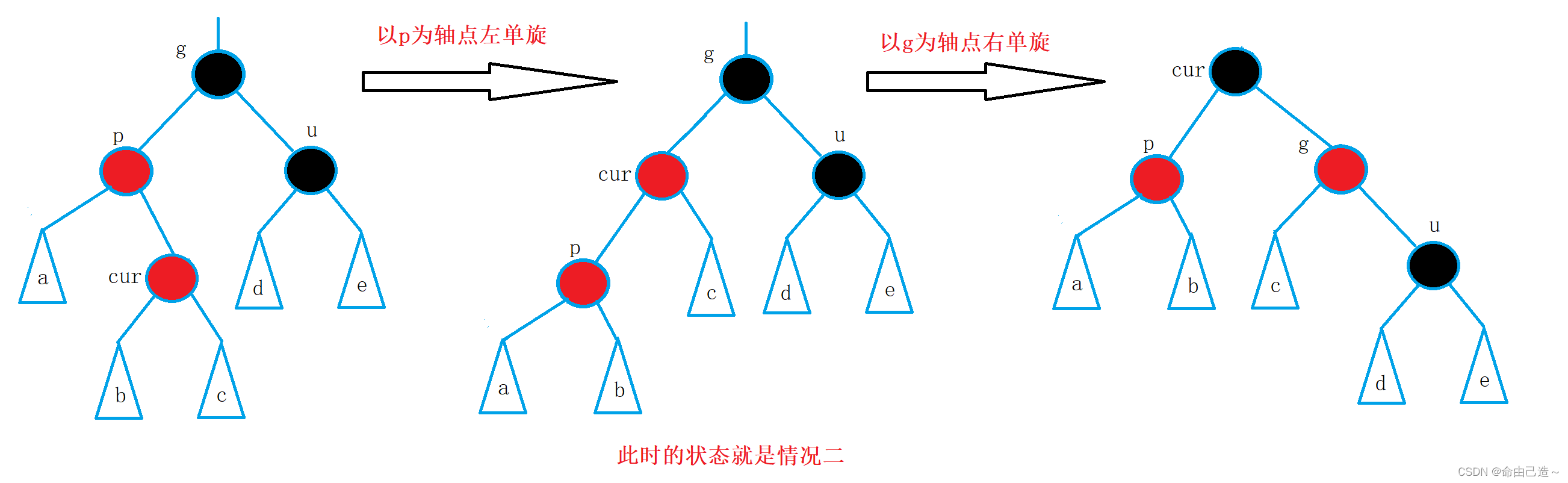
以上三种情况的代码如下:
while (parent && parent->_col == RED)
{// 找g 与 uNode* g = parent->_parent;if (parent == g->_left){Node* u = g->_right;// 情况一 u存在且为红if (u && u->_col == RED){parent->_col = u->_col = BLACK;g->_col = RED;// 继续往上处理cur = g;parent = cur->_parent;}else // 情况二或情况三{if (cur == parent->_left)// 情况二{// g// p// cRotateR(g);parent->_col = BLACK;g->_col = RED;}else// 情况三{// g// p// cRotateL(parent);RotateR(g);// c// p gcur->_col = BLACK;g->_col = RED;}break;}}else{Node* u = g->_left;// 情况一if (u && u->_col == RED){u->_col = parent->_col = BLACK;g->_col = RED;cur = g;parent = cur->_parent;}else{// 情况二// g// p// cif (cur == parent->_right){RotateL(g);parent->_col = BLACK;g->_col = RED;}else// 情况三{// g// p// cRotateR(parent);RotateL(g);cur->_col = BLACK;g->_col = RED;}break;}}
}
// 上面有可能把_root的颜色变为红
_root->_col = BLACK;
return true;
}
三、验证
想要验证是否是红黑树,首先要保证是搜索树(中序遍历有序)。
其次还要判断根节点是否为黑,是否有两个红的相连(检查红节点的父亲),每条路径上的黑节点数目相同(随便找一条路径测出标准值)。
怎么测每条路径的黑节点数目是否相同?
测一条路径的黑节点数目当作标准值,递归过程中遇到黑节点就记录,到空说明该路径走完,比对标准值,如果不同就返回false。
bool _IsBalance(Node* root, int i, int flag)
{if (root == nullptr){if (i != flag){cout << "errno: 左右子树黑色节点数目不同" << endl;return false;}return true;}// 红节点时判断父亲if (root->_col == RED){if (root->_parent->_col == RED){cout << "errno: 红-红" << endl;return false;}}if (root->_col == BLACK){i++;}return _IsBalance(root->_left, i, flag) && _IsBalance(root->_right, i, flag);
}bool IsBalance()
{if (_root == nullptr){return true;}if (_root->_col != BLACK){return false;}// 找标准值Node* cur = _root;int flag = 0;while (cur){if (cur->_col == BLACK){flag++;}cur = cur->_left;}int i = 0;return _IsBalance(_root, i, flag);
}
四、源码
#pragma once
#include <iostream>
#include <cstdlib>
#include <cassert>
#include <string>using namespace std;enum Colour
{RED,BLACK,
};template <class K, class V>
struct RBTreeNode
{RBTreeNode(const pair<K, V>& kv): _kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;
};template <class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:bool insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else return false;}cur = new Node(kv);if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent && parent->_col == RED){// 找g 与 uNode* g = parent->_parent;if (parent == g->_left){Node* u = g->_right;// 情况一 u存在且为红if (u && u->_col == RED){parent->_col = u->_col = BLACK;g->_col = RED;// 继续往上处理cur = g;parent = cur->_parent;}else // 情况二或情况三{if (cur == parent->_left)// 情况二{// g// p// cRotateR(g);parent->_col = BLACK;g->_col = RED;}else// 情况三{// g// p// cRotateL(parent);RotateR(g);// c// p gcur->_col = BLACK;g->_col = RED;}break;}}else{Node* u = g->_left;// 情况一if (u && u->_col == RED){u->_col = parent->_col = BLACK;g->_col = RED;cur = g;parent = cur->_parent;}else{// 情况二// g// p// cif (cur == parent->_right){RotateL(g);parent->_col = BLACK;g->_col = RED;}else// 情况三{// g// p// cRotateR(parent);RotateL(g);cur->_col = BLACK;g->_col = RED;}break;}}}// 上面有可能把_root的颜色变为红_root->_col = BLACK;return true;}void RotateL(Node* parent){Node* top = parent->_parent;Node* right = parent->_right;parent->_right = right->_left;if (right->_left) right->_left->_parent = parent;right->_left = parent;parent->_parent = right;if (top)// 子树{if (parent == top->_left) top->_left = right;else top->_right = right;right->_parent = top;}else// 完整的树{_root = right;_root->_parent = nullptr;}}void RotateR(Node* parent){Node* top = parent->_parent;Node* left = parent->_left;Node* leftR = left->_right;parent->_left = leftR;if (leftR) leftR->_parent = parent;left->_right = parent;parent->_parent = left;if (top){if (parent == top->_left) top->_left = left;else top->_right = left;left->_parent = top;}else{_root = left;_root->_parent = nullptr;}}void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << "<=>" << root->_kv.second << endl;_Inorder(root->_right);}void Inorder(){_Inorder(_root);}bool _IsBalance(Node* root, int i, int flag){if (root == nullptr){if (i != flag){cout << "errno: 左右子树黑色节点数目不同" << endl;return false;}return true;}// 红节点时判断父亲if (root->_col == RED){if (root->_parent->_col == RED){cout << "errno: 红-红" << endl;return false;}}if (root->_col == BLACK){i++;}return _IsBalance(root->_left, i, flag) && _IsBalance(root->_right, i, flag);}bool IsBalance(){if (_root == nullptr){return true;}if (_root->_col != BLACK){return false;}// 找标准值Node* cur = _root;int flag = 0;while (cur){if (cur->_col == BLACK){flag++;}cur = cur->_left;}int i = 0;return _IsBalance(_root, i, flag);}private:Node* _root = nullptr;
};void test()
{RBTree<int, int> bb;const int N = 10000;srand(time(0));for (int i = 0; i < N; i++){size_t x = rand();bb.insert(make_pair(x, x));}/*int a[] = { 16, 3, 7, 11, 9, 26, 18, 14};for (auto e : a){bb.insert(make_pair(e, e));}*/cout << bb.IsBalance();
}
相关文章:

【数据结构】红黑树
红黑树一、红黑树的概念二、红黑树的接口2.1 插入三、验证四、源码一、红黑树的概念 红黑树也是一个二叉搜索树,他是通过对任何一条从根到叶子的路径上各个结点着色方式的限制,最长路径长度不超过最短路径长度的 2 倍保持近似平衡。他在每个节点添加了一…...

从C++的角度理解C#的Event
由于技术背景是C起家的,所以对于C的概念很清楚,遇到C#的EVENT时候,总感觉这个概念比较抽象,不容易理解,但是当使用函数指针和回调函数来理解EVENT的时候,这个概念就清晰了。 首先对于EVENT来讲,…...
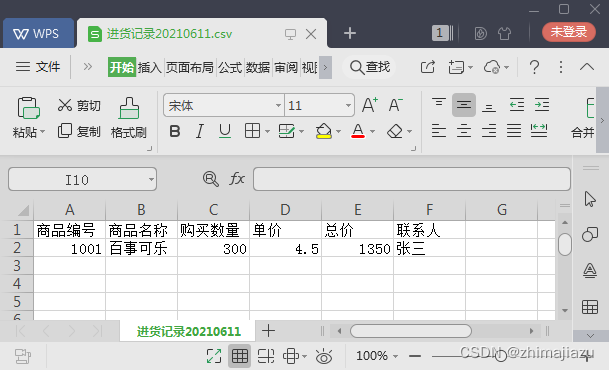
商城进货记录交易-课后程序(JAVA基础案例教程-黑马程序员编著-第七章-课后作业)
【实验7-2】商城进货记录交易 【任务介绍】 1.任务描述 每个商城都需要进货,而这些进货记录整理起来很不方便,本案例要求编写一个商城进货记录交易的程序,使用字节流将商场的进货信息记录在本地的csv文件中。程序具体要求如下: …...
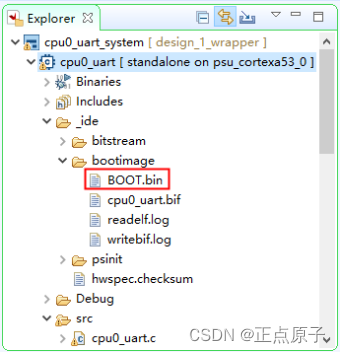
【正点原子FPGA连载】第十七章双核AMP实验 摘自【正点原子】DFZU2EG_4EV MPSoC之嵌入式Vitis开发指南
1)实验平台:正点原子MPSoC开发板 2)平台购买地址:https://detail.tmall.com/item.htm?id692450874670 3)全套实验源码手册视频下载地址: http://www.openedv.com/thread-340252-1-1.html 第十七章双核AMP…...
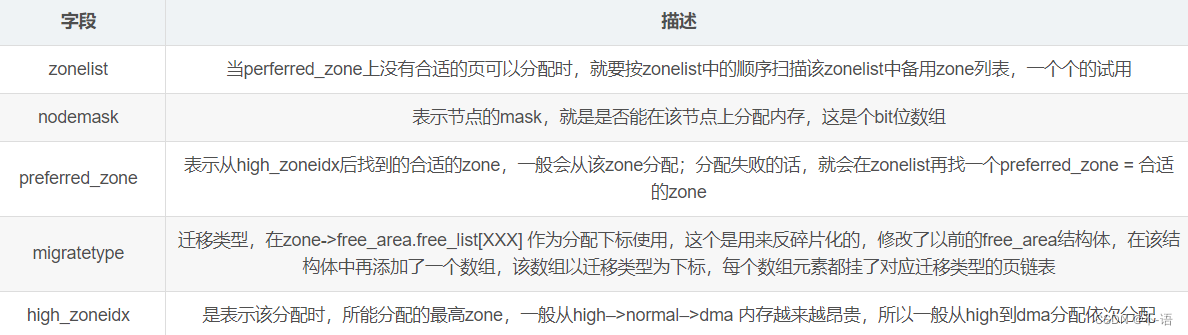
内存管理框架---页(一)
文章目录物理内存的模型非一致内存访问--NUMA一致内存访问模型--UMA内存管理架构页页框管理页描述符页描述符字段flags字段详解gfp_mask 标志获得页alloc_pages__get_free_pages获得填充为0的页释放页kmallocvmalloc参考资料你用心写的每一篇文章,可能会带别人和自己…...
)
华为OD机试真题Python实现【流水线】真题+解题思路+代码(20222023)
流水线 题目 一个工厂有m条流水线 来并行完成n个独立的作业 该工厂设置了一个调度系统 在安排作业时,总是优先执行处理时间最短的作业 现给定流水线个数m 需要完成的作业数n 每个作业的处理时间分别为 t1,t2...tn 请你编程计算处理完所有作业的耗时为多少 当n > m时 首先…...
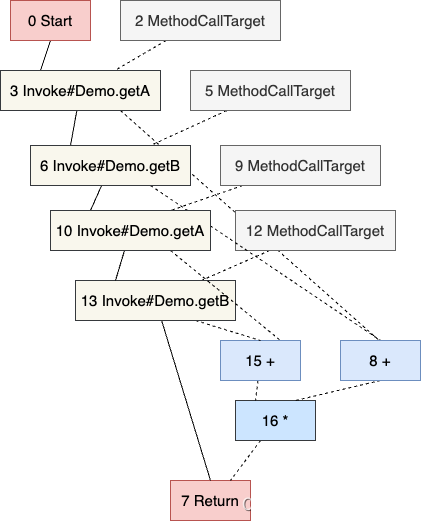
「JVM 编译优化」Graal 编译器
文章目录1. 历史背景2. 构建编译调试环境3. JVMCI 编译器接口4. 代码中间表示5. 代码优化与生成1. 历史背景 Graal 编译器在 JDK 9 以 Jaotc 提前编译工具的形式首次加入到官方的 JDK 中,JDK 10 开始提供替换(得益于 HotSpot 编译器接口,Jav…...

蓝牙标签操作指南
一、APP安装指南 1.APP权限问题 电子标签APP安装之后,会提示一些权限的申请,点击允许。否则某些会影响APP的正常运行。安装后,搜索不到蓝牙标签,可以关闭App,重新打开。 2.手机功能 运行APP时候,需要打开…...

嵌入式 Linux Shell编程
目录 1、shell脚本 2、执行shell脚本 3、shell脚本编写 3.1 shell变量 3.2 标准变量或环境变量 3.4 变量赋值有五种格式 3.5 运算符和表达式 关系运算符 布尔运算符 3.6 Test命令用法 1、判断表达式 2、判断字符串 3.判断整数 4、判断文件 3.7 数组 1、数组定义…...
Web前端学习:一
编辑器的基础使用 编辑器推荐使用: HBuilderx(免费中文)(建议使用) Sublime(免费英文) Sublime中文设置方法,下载语言插件: 1、进入Sublime后,ShiftCtrlP…...

SpringBoot集成Redis实现分布式会话
在单体应用的时代,Session 会话直接保存在服务器中,实现非常简单,但是随着微服务的流行,现代应用架构基本都是分布式架构,请求随机的分配到后端的多个应用中,此时session就需要共享,而存储在red…...
2023年关于身份安全的4 个预测
如果您身处技术领域,就会知道现在是时候盘点过去的一年,展望未来 365 天将影响业务、创新以及我们工作方式的因素的季节。这不是一门精确的科学,我们也不总是对的。但是推测很有趣,当我们看到其中一些趋势成为现实时会更有趣。本文…...

Linux期末考试应急
Linux期末考试应急 虚拟机添加硬盘、分区、格式化、挂载、卸载 fdisk -l#查看系统现有分区fdisk <指定磁盘>#指定磁盘分区sudo mkfs.ext3 <指定分区>#格式化磁盘###挂载磁盘1.新建一个目录sudo mkdir /mnt/test2.将指定分区挂载到对应目录sudo mount /dev/sdb10 /…...
mars3d对geojson图层分属性设置样式
开发中可能会遇到如下需求,在全省的数据中按某个属性⾼亮展示某市区。此时就需要使⽤分属性样式的api了。⽂档如下。GeoJsonLayer - Mars3D API文档属性是根据⽮量数据的属性进⾏匹配。可以通过 layer.graphics[0]?.attr ⽅式获取。 指导有哪些属性之后先设置…...
三、锁相关知识
文章目录锁的分类可重入锁、不可重入锁乐观锁、悲观锁公平锁、非公平锁互斥锁、共享锁深入synchronized类锁、对象锁synchronized的优化synchronized实现原理synchronized的锁升级重量锁底层ObjectMonitor深入ReentrantLockReentrantLock和synchronized的区别AQS概述加锁流程源…...

C语言数据类型
C 数据类型 在 C 语言中,数据类型指的是用于声明不同类型的变量或函数的一个广泛的系统。变量的类型决定了变量存储占用的空间,以及如何解释存储的位模式。 C 中的类型可分为以下几种: 1 基本类型: 它们是算术类型,…...
)
华为OD机试真题Python实现【水仙花数】真题+解题思路+代码(20222023)
水仙花数 题目 所谓的水仙花数是指一个n位的正整数其各位数字的n次方的和等于该数本身, 例如153 = 1^3 + 5^3 + 3^3,153是一个三位数 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Python)真题目录汇总 输入 第一行输入一个整数N, 表示 N 位的正整数 N 在3…...

【华为OD机试模拟题】用 C++ 实现 - 非严格递增连续数字序列(2023.Q1)
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...

RN面试题
RN面试题1.React Native相对于原生的ios和Android有哪些优势?1.性能媲美原生APP 2.使用JavaScript编码,只要学习这一种语言 3.绝大部分代码安卓和IOS都能共用 4.组件式开发,代码重用性很高 5.跟编写网页一般,修改代码后即可自动刷…...
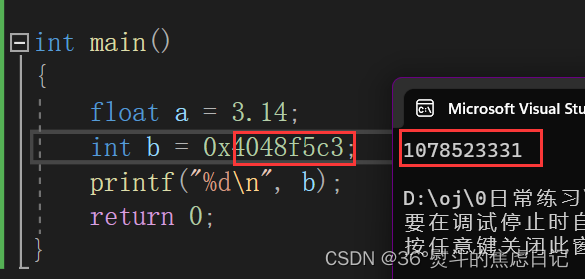
【数据存储】浮点型在内存中的存储
目录 一、存储现象 二、IEEE标准规范 1.存储 2.读取 三、举例验证 1.存储 2.读取 浮点型存储的标准是IEEE(电气电子工程师学会)754制定的。 一、存储现象 浮点数由于其有小数点的特殊性,有很多浮点数是不能精确存储的,如&#…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...
