深度学习在 NumPy、TensorFlow 和 PyTorch 中实现所有损失函数
目录
一、说明
二、内容提示
三、均方误差 (MSE) 损失
3.1 NumPy 中的实现
3.2 在 TensorFlow 中的实现
3.3 在 PyTorch 中的实现
四、二元交叉熵损失
4.1 NumPy 中的实现
4.2 在 TensorFlow 中的实现
4.3 在 PyTorch 中的实现
五、加权二元交叉熵损失
5.1 分类交叉熵损失
5.2 NumPy 中的实现
5.3 在 TensorFlow 中的实现
六、稀疏分类交叉熵损失
6.1 NumPy 中的实现
6.2 在 TensorFlow 中的实现
6.3 在 PyTorch 中的实现
七、骰子损失
7.1 NumPy 中的实现
7.2 在 TensorFlow 中的实现
7.3 在 PyTorch 中的实现
八、KL 散度损失
8.1 NumPy 中的实现
8.2 在 TensorFlow 中的实现
8.3 在 PyTorch 中的实现
九、平均绝对误差 (MAE) 损耗/L1 损耗
9.1 Numpy 中的实现
9.2 在 TensorFlow 中的实现
9.3 在 PyTorch 中的实现
十、胡贝尔损失
10.1 Numpy 中的实现
10.2 在 TensorFlow 中的实现
10.3 在 PyTorch 中的实现
一、说明
损失函数有多种,深度学习开发平台也有许多,那么用多种平台实现多种损失函数,会有什么结论?本篇对比实现多种跨平台对多种损失函数的实现。
二、内容提示
- 均方误差 (MSE) 损失
- 二元交叉熵损失
- 加权二元交叉熵损失
- 分类交叉熵损失
- 稀疏分类交叉熵损失
- 骰子损失
- KL 散度损失
- 平均绝对误差 (MAE) / L1 损耗
- 胡贝尔损失
三、均方误差 (MSE) 损失
均方误差 (MSE) 损失是回归问题中常用的损失函数,其目标是预测连续变量。损失计算为预测值和真实值之间的平方差的平均值。MSE损失的公式为:
MSE 损失 = (1/n) * sum((y_pred — y_true)²)
在这里:
- n 是数据集中的样本数
- y_pred 是目标变量的预测值
- y_true 是目标变量的真实值
MSE 损失对异常值很敏感,并且会严重惩罚大错误,这在某些情况下可能是不可取的。在这种情况下,可以使用其他损失函数,例如平均绝对误差 (MAE) 或 Huber 损失。
3.1 NumPy 中的实现
import numpy as npdef mse_loss(y_pred, y_true):"""Calculates the mean squared error (MSE) loss between predicted and true values.Args:- y_pred: predicted values- y_true: true valuesReturns:- mse_loss: mean squared error loss"""n = len(y_true)mse_loss = np.sum((y_pred - y_true) ** 2) / nreturn mse_loss 在此实现中,y_pred和y_true是分别包含预测值和真实值的 NumPy 数组。y_pred该函数首先计算和之间的平方差y_true,然后取这些值的平均值以获得 MSE 损失。该n变量表示数据集中的样本数量,用于标准化损失。
3.2 在 TensorFlow 中的实现
import tensorflow as tfdef mse_loss(y_pred, y_true):"""Calculates the mean squared error (MSE) loss between predicted and true values.Args:- y_pred: predicted values- y_true: true valuesReturns:- mse_loss: mean squared error loss"""mse = tf.keras.losses.MeanSquaredError()mse_loss = mse(y_true, y_pred)return mse_loss在此实现中,y_pred 和 y_true 是分别包含预测值和真实值的 TensorFlow 张量。 tf.keras.losses.MeanSquaredError() 函数计算 y_pred 和 y_true 之间的 MSE 损失。 mse_loss 变量包含计算出的损失。
3.3 在 PyTorch 中的实现
import torchdef mse_loss(y_pred, y_true):"""Calculates the mean squared error (MSE) loss between predicted and true values.Args:- y_pred: predicted values- y_true: true valuesReturns:- mse_loss: mean squared error loss"""mse = torch.nn.MSELoss()mse_loss = mse(y_pred, y_true)return mse_loss在此实现中,y_pred 和 y_true 是分别包含预测值和真实值的 PyTorch 张量。 torch.nn.MSELoss() 函数计算 y_pred 和 y_true 之间的 MSE 损失。 mse_loss 变量包含计算出的损失。
四、二元交叉熵损失
二元交叉熵损失,也称为对数损失,是二元分类问题中常用的损失函数。它测量预测概率分布和实际二元标签分布之间的差异。
二元交叉熵损失的公式如下:
L(y, ŷ) = -[y * log(ŷ) + (1 — y) * log(1 — ŷ)]
其中 y 是真实的二元标签(0 或 1),ŷ 是预测概率(范围从 0 到 1),log 是自然对数。
方程第一项计算真实标签为1时的损失,第二项计算真实标签为0时的损失。总损失是两项之和。
当预测概率接近真实标签时,损失较低,而当预测概率远离真实标签时,损失较高。该损失函数通常用于在输出层使用 sigmoid 激活函数来预测二进制标签的神经网络模型。
4.1 NumPy 中的实现
在numpy中,二元交叉熵损失可以使用我们之前描述的公式来实现。以下是如何计算的示例:
# define true labels and predicted probabilities
y_true = np.array([0, 1, 1, 0])
y_pred = np.array([0.1, 0.9, 0.8, 0.3])# calculate the binary cross-entropy loss
loss = -(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred)).mean()# print the loss
print(loss)4.2 在 TensorFlow 中的实现
在TensorFlow中,二元交叉熵损失可以使用tf.keras.losses.BinaryCrossentropy()函数来实现。以下是如何使用它的示例:
import tensorflow as tf# define true labels and predicted probabilities
y_true = tf.constant([0, 1, 1, 0])
y_pred = tf.constant([0.1, 0.9, 0.8, 0.3])# define the loss function
bce_loss = tf.keras.losses.BinaryCrossentropy()# calculate the loss
loss = bce_loss(y_true, y_pred)# print the loss
print(loss)4.3 在 PyTorch 中的实现
在PyTorch中,可以使用该torch.nn.BCELoss()函数实现二元交叉熵损失。以下是如何使用它的示例:
import torch# define true labels and predicted probabilities
y_true = torch.tensor([0, 1, 1, 0], dtype=torch.float32)
y_pred = torch.tensor([0.1, 0.9, 0.8, 0.3], dtype=torch.float32)# define the loss function
bce_loss = torch.nn.BCELoss()# calculate the loss
loss = bce_loss(y_pred, y_true)# print the loss
print(loss)
五、加权二元交叉熵损失
加权二元交叉熵损失是二元交叉熵损失的一种变体,它允许为正例和负例分配不同的权重。这在处理不平衡的数据集时非常有用,其中一个类别与另一类别相比明显不足。
加权二元交叉熵损失的公式如下:
L(y, ŷ) = -[w_pos * y * log(ŷ) + w_neg * (1 — y) * log(1 — ŷ)]
其中 y 是真实的二元标签(0 或 1),ŷ 是预测概率(范围从 0 到 1),log 是自然对数,w_pos 和 w_neg 分别是正权重和负权重。
方程第一项计算真实标签为 1 时的损失,第二项计算真实标签为 0 时的损失。总损失是两项的总和,每项都按相应的权重进行加权。
可以根据每个类别的相对重要性来选择正权重和负权重。例如,如果正类别更重要,则可以为其分配更高的权重。类似地,如果负类更重要,则可以为其分配更高的权重。
当预测概率接近真实标签时,损失较低,而当预测概率远离真实标签时,损失较高。该损失函数通常用于在输出层使用 sigmoid 激活函数来预测二进制标签的神经网络模型。
5.1 分类交叉熵损失
分类交叉熵损失是多类分类问题中常用的损失函数。它测量每个类别的真实标签和预测概率之间的差异。
分类交叉熵损失的公式为:
L = -1/N * sum(sum(Y * log(Y_hat))) 其中Y是 one-hot 编码格式的真实标签矩阵,Y_hat是每个类别的预测概率矩阵,N是样本数,log表示自然对数。
在此公式中, 的Y形状为(N, C),其中N是样本数,C是类别数。的每一行Y代表单个样本的真实标签分布,真实标签对应的列值为 1,所有其他列值为 0。
类似地,Y_hat具有 的形状(N, C),其中每行表示单个样本的预测概率分布,以及每个类别的概率值。
该log函数按元素应用于预测概率矩阵Y_hat。该sum函数使用两次来对矩阵的两个维度求和Y。
所得值表示数据集中L所有样本的平均交叉熵损失。N训练神经网络的目标是最小化该损失函数。
损失函数会更严厉地惩罚模型在预测低概率类时犯下的大错误。目标是最小化损失函数,这意味着使预测概率尽可能接近真实标签。
5.2 NumPy 中的实现
在 numpy 中,分类交叉熵损失可以使用我们之前描述的公式来实现。以下是如何计算的示例:
import numpy as np# define true labels and predicted probabilities as NumPy arrays
y_true = np.array([[0, 1, 0], [0, 0, 1], [1, 0, 0]])
y_pred = np.array([[0.8, 0.1, 0.1], [0.2, 0.3, 0.5], [0.1, 0.6, 0.3]])# calculate the loss
loss = -1/len(y_true) * np.sum(np.sum(y_true * np.log(y_pred)))# print the loss
print(loss)In this example, y_true represents the true labels (in integer format), and y_pred represents the predicted probabilities for each class (in a 2D array). The eye() function is used to convert the true labels to one-hot encoding, which is required for the loss calculation. The categorical cross-entropy loss is calculated using the formula we provided earlier, and the mean() function is used to average the loss over the entire dataset. Finally, the calculated loss is printed to the console. 在此示例中,y_true表示 one-hot 编码格式的真实标签,并y_pred表示每个类别的预测概率,两者均以 NumPy 数组形式表示。使用上述公式计算损失,然后使用该print函数将其打印到控制台。请注意,该np.sum函数使用两次来对Y矩阵的两个维度求和。
5.3 在 TensorFlow 中的实现
在 TensorFlow 中,可以使用该类轻松计算分类交叉熵损失tf.keras.losses.CategoricalCrossentropy。以下是如何使用它的示例:
import tensorflow as tf# define true labels and predicted probabilities as TensorFlow Tensors
y_true = tf.constant([[0, 1, 0], [0, 0, 1], [1, 0, 0]])
y_pred = tf.constant([[0.8, 0.1, 0.1], [0.2, 0.3, 0.5], [0.1, 0.6, 0.3]])# create the loss object
cce_loss = tf.keras.losses.CategoricalCrossentropy()# calculate the loss
loss = cce_loss(y_true, y_pred)# print the loss
print(loss.numpy())在此示例中,y_true 表示 one-hot 编码格式的真实标签,y_pred 表示每个类的预测概率,两者均为 TensorFlow 张量。 CategoricalCrossentropy 类用于创建损失函数的实例,然后通过传入真实标签和预测概率作为参数来计算损失。最后,使用 .numpy() 方法将计算出的损失打印到控制台。
请注意,CategoricalCrossentropy 类在内部处理真实标签到 one-hot 编码的转换,因此您不需要显式执行此操作。如果您的真实标签已经采用 one-hot 编码格式,您可以将它们直接传递到损失函数,不会出现任何问题。
在 PyTorch 中的实现
在 PyTorch 中,可以使用该类轻松计算分类交叉熵损失torch.nn.CrossEntropyLoss。以下是如何使用它的示例:
<span style="color:rgba(0, 0, 0, 0.8)"><span style="background-color:#ffffff"><span style="background-color:#f9f9f9"><span style="color:#242424">import torch <span style="color:#007400"># 将真实标签和预测逻辑定义为 PyTorch Tensors</span>y_true = torch.LongTensor([1, 2, 0])
y_logits = torch.Tensor([[0.8, 0.1, 0.1], [0.2, 0.3, 0.5], [ 0.1, 0.6, 0.3]]) <span style="color:#007400"># 创建损失对象</span>
ce_loss = torch.nn.CrossEntropyLoss() <span style="color:#007400"># 计算损失</span>
loss = ce_loss(y_logits, y_true) <span style="color:#007400"># 打印损失</span>
print(loss.item())</span></span></span></span>在此示例中,y_true以整数格式表示真实标签,并y_logits表示每个类的预测逻辑,两者均以 PyTorch 张量形式表示。该类CrossEntropyLoss用于创建损失函数的实例,然后通过传入预测的 logits 和真实标签作为参数来计算损失。最后,使用该方法将计算出的损失打印到控制台.item()。
请注意,该类CrossEntropyLoss将 softmax 激活函数和分类交叉熵损失合并到单个操作中,因此您不需要单独应用 softmax。另请注意,真正的标签应该是整数格式,而不是 one-hot 编码格式。
六、稀疏分类交叉熵损失
稀疏分类交叉熵损失与分类交叉熵损失类似,但它在真实标签以整数而不是 one-hot 编码形式提供时使用。它通常用作多类分类问题中的损失函数。
稀疏分类交叉熵损失的公式为:
L = -1/N * sum(log(Y_hat_i))其中 Y_hat_i 是每个样本的真实类标签 i 的预测概率,N 是样本数。
换句话说,该公式计算每个样本的真实类标签的预测概率的负对数,然后对所有样本对这些值进行平均。
与对真实标签使用单热编码的分类交叉熵损失不同,稀疏分类交叉熵损失直接使用整数标签。每个样本的真实标签表示为 0 到 C-1 之间的单个整数值 i,其中 C 是类别数。
6.1 NumPy 中的实现
import numpy as npdef sparse_categorical_crossentropy(y_true, y_pred):# convert true labels to one-hot encodingy_true_onehot = np.zeros_like(y_pred)y_true_onehot[np.arange(len(y_true)), y_true] = 1# calculate lossloss = -np.mean(np.sum(y_true_onehot * np.log(y_pred), axis=-1))return loss 在此实现中,y_true是整数标签数组,y_pred是每个样本的预测概率数组。该函数首先使用 NumPy 的高级索引功能将真实标签转换为 one-hot 编码格式,以创建一个形状数组,其中 是(N, C)样本N数,C是类数,每行对应于单个样本的真实标签分布样本。
然后该函数使用前面答案中描述的公式计算损失:-1/N * sum(log(Y_hat_i))。这是使用 NumPy 的广播来实现的,其中y_true_onehot * np.log(y_pred)创建一个形状数组(N, C),其中每个元素代表 和 中相应元素的y_true_onehot乘积np.log(y_pred)。然后,该sum函数用于对C维度进行求和,并mean用于对N维度进行平均。
以下是如何使用该函数的示例:
# define true labels as integers and predicted probabilities as an array
y_true = np.array([1, 2, 0])
y_pred = np.array([[0.1, 0.8, 0.1], [0.3, 0.2, 0.5], [0.4, 0.3, 0.3]])# calculate the loss
loss = sparse_categorical_crossentropy(y_true, y_pred)# print the loss
print(loss)这将输出给定输入的稀疏分类交叉熵损失的值。
6.2 在 TensorFlow 中的实现
import tensorflow as tfdef sparse_categorical_crossentropy(y_true, y_pred):loss = tf.keras.losses.sparse_categorical_crossentropy(y_true, y_pred, from_logits=False)return loss# define true labels as integers and predicted probabilities as a tensor
y_true = tf.constant([1, 2, 0])
y_pred = tf.constant([[0.1, 0.8, 0.1], [0.3, 0.2, 0.5], [0.4, 0.3, 0.3]])# calculate the loss
loss = sparse_categorical_crossentropy(y_true, y_pred)# print the loss
print(loss.numpy()) 在此实现中,y_true是整数标签数组,y_pred是每个样本的预测概率数组。该函数使用tf.keras.losses.sparse_categorical_crossentropyTensorFlow提供的函数来计算损失。该from_logits参数设置False为确保y_pred代表概率而不是 logit 值。
6.3 在 PyTorch 中的实现
import torch.nn.functional as F
import torchdef sparse_categorical_crossentropy(y_true, y_pred):loss = F.cross_entropy(y_pred, y_true)return loss# define true labels as integers and predicted logits as a tensor
y_true = torch.tensor([1, 2, 0])
y_pred = torch.tensor([[0.1, 0.8, 0.1], [0.3, 0.2, 0.5], [0.4, 0.3, 0.3]])# calculate the loss
loss = sparse_categorical_crossentropy(y_true, y_pred)# print the loss
print(loss.item()) 在此实现中,y_true是整数标签数组,y_pred是每个样本的预测逻辑数组。该函数使用PyTorch的F.cross_entropy函数来计算损失。张y_pred量应该具有形状(N, C),其中N是样本数,C是类数。
七、骰子损失
Dice 损失,也称为 Sørensen-Dice 系数或 F1 分数,是图像分割任务中使用的损失函数,用于测量预测分割与地面实况之间的重叠。Dice 损失范围从 0 到 1,其中 0 表示没有重叠,1 表示完全重叠。
Dice 损失定义为:
Dice Loss = 1 - (2 * intersection + smooth) / (sum of squares of prediction + sum of squares of ground truth + smooth) 其中intersection是预测和真实掩模的逐元素乘积,smooth是一个平滑常数(通常是一个小值,例如 1e-5),以防止被零除,并且对掩模的所有元素进行求和。
Dice 损失可以在各种深度学习框架中实现,例如 TensorFlow、PyTorch 和 NumPy。该实现涉及使用框架中可用的逐元素乘积和求和运算来计算交集和平方和。
7.1 NumPy 中的实现
import numpy as npdef dice_loss(y_true, y_pred, smooth=1e-5):intersection = np.sum(y_true * y_pred, axis=(1,2,3))sum_of_squares_pred = np.sum(np.square(y_pred), axis=(1,2,3))sum_of_squares_true = np.sum(np.square(y_true), axis=(1,2,3))dice = 1 - (2 * intersection + smooth) / (sum_of_squares_pred + sum_of_squares_true + smooth)return dice 在此实现中,y_true和y_pred分别是真实值和预测掩模。该smooth参数用于防止被零除。和函数分别用于计算交集sum和square平方和。最后,使用前面答案中描述的公式计算 Dice 损失。
请注意,此实现假设y_true和y_pred是维度为 的 4D 数组(batch_size, height, width, num_classes)。如果您的蒙版具有不同的形状,您可能需要相应地修改实现。
7.2 在 TensorFlow 中的实现
import tensorflow as tfdef dice_loss(y_true, y_pred, smooth=1e-5):intersection = tf.reduce_sum(y_true * y_pred, axis=(1,2,3))sum_of_squares_pred = tf.reduce_sum(tf.square(y_pred), axis=(1,2,3))sum_of_squares_true = tf.reduce_sum(tf.square(y_true), axis=(1,2,3))dice = 1 - (2 * intersection + smooth) / (sum_of_squares_pred + sum_of_squares_true + smooth)return dice 在此实现中,y_true和y_pred是 TensorFlow 张量,分别表示地面实况和预测掩模。该smooth参数用于防止被零除。和函数分别用于计算交集reduce_sum和square平方和。最后,使用前面答案中描述的公式计算 Dice 损失。
请注意,此实现假设y_true和y_pred是维度为 的 4D 张量(batch_size, height, width, num_classes)。如果您的蒙版具有不同的形状,您可能需要相应地修改实现。
7.3 在 PyTorch 中的实现
import torchdef dice_loss(y_true, y_pred, smooth=1e-5):intersection = torch.sum(y_true * y_pred, dim=(1,2,3))sum_of_squares_pred = torch.sum(torch.square(y_pred), dim=(1,2,3))sum_of_squares_true = torch.sum(torch.square(y_true), dim=(1,2,3))dice = 1 - (2 * intersection + smooth) / (sum_of_squares_pred + sum_of_squares_true + smooth)return dice 在此实现中,y_true和y_pred是 PyTorch 张量,分别表示地面实况和预测掩模。该smooth参数用于防止被零除。和函数分别用于计算交集sum和square平方和。最后,使用前面答案中描述的公式计算 Dice 损失。
请注意,此实现假设y_true和y_pred是维度为 的 4D 张量(batch_size, num_classes, height, width)。如果您的蒙版具有不同的形状,您可能需要相应地修改实现。
八、KL 散度损失
KL(Kullback-Leibler)散度损失是衡量两个概率分布彼此差异程度的指标。在机器学习的背景下,它通常用作损失函数来训练从给定分布生成新样本的模型。
两个概率分布 p 和 q 之间的 KL 散度定义为:
KL(p||q) = sum(p(x) * log(p(x) / q(x)))
在机器学习的背景下,p 代表真实分布,q 代表预测分布。KL 散度损失衡量预测分布与真实分布的匹配程度。
KL散度损失可用于图像生成、文本生成和强化学习等各种任务。然而,由于它具有非凸形式,因此可能很难优化。
在实践中,KL散度损失通常与其他损失函数(例如交叉熵损失)结合使用。通过将 KL 散度损失添加到交叉熵损失中,鼓励模型生成不仅与目标分布匹配而且与训练数据具有相似分布的样本。
8.1 NumPy 中的实现
import numpy as npdef kl_divergence_loss(p, q):return np.sum(p * np.log(p / q)) 在此实现中,p和q是分别表示真实分布和预测分布的 numpy 数组。KL 散度损失是使用上述公式计算的。
请注意,此实现假设p和q具有相同的形状。如果它们具有不同的形状,您可能需要相应地修改实现。
8.2 在 TensorFlow 中的实现
tf.keras.losses.KLDivergence()是 TensorFlow 中的内置函数,用于计算两个概率分布之间的 KL 散度损失。它可以用作图像生成、文本生成和强化学习等各种机器学习任务中的损失函数。
以下是 的用法示例tf.keras.losses.KLDivergence():
import tensorflow as tf# define true distribution and predicted distribution
p = tf.constant([0.2, 0.3, 0.5])
q = tf.constant([0.4, 0.3, 0.3])# compute KL divergence loss
kl_loss = tf.keras.losses.KLDivergence()(p, q)print(kl_loss.numpy()) 在此示例中,p和q是分别表示真实分布和预测分布的 TensorFlow 张量。该tf.keras.losses.KLDivergence()函数用于计算p和之间的 KL 散度损失q。结果是表示损失值的标量张量。
请注意,tf.keras.losses.KLDivergence() 通过将 p 和 q 广播为通用形状来自动处理 p 和 q 具有不同形状的情况。此外,您可以通过设置函数的归约参数来调整 KL 散度损失相对于模型中其他损失的权重,该参数控制损失的聚合方式。
8.3 在 PyTorch 中的实现
在 PyTorch 中,可以使用该模块计算 KL 散度损失torch.nn.KLDivLoss。这是一个示例实现:
import torchdef kl_divergence_loss(p, q):criterion = torch.nn.KLDivLoss(reduction='batchmean')loss = criterion(torch.log(p), q)return lossIn this implementation, p and q are PyTorch tensors representing the true distribution and predicted distribution, respectively. The torch.nn.KLDivLoss module is used to compute the KL divergence loss between p and q. The reduction parameter is set to 'batchmean' to compute the mean loss over the batch. 请注意,p和q应该是概率,并且沿最后一个维度总和为 1。该torch.log函数用于在p将其传递给torch.nn.KLDivLoss模块之前对其取对数。这是因为该模块期望输入是对数概率。
九、平均绝对误差 (MAE) 损耗/L1 损耗
L1 损失,也称为平均绝对误差 (MAE) 损失,是深度学习回归任务中常用的损失函数。它测量目标变量的预测值和真实值之间的绝对差异。
L1损失的公式为:
L1 损失 = 1/n * Σ|y_pred — y_true|
其中n是样本数,y_pred是预测值,y_true是真实值。
简单来说,L1 损失是预测值和真实值之间的绝对差的平均值。它对异常值的敏感度低于均方误差 (MSE) 损失,因此对于可能受异常值影响的模型来说,它是一个不错的选择。
9.1 Numpy 中的实现
import numpy as npdef l1_loss(y_pred, y_true):loss = np.mean(np.abs(y_pred - y_true))return lossL1 损失的 NumPy 实现与公式非常相似,从真实值中减去预测值并取绝对值。然后,取所有样本中这些绝对差的平均值,以获得平均 L1 损失。
9.2 在 TensorFlow 中的实现
import tensorflow as tfdef l1_loss(y_pred, y_true):loss = tf.reduce_mean(tf.abs(y_pred - y_true))return loss 在 TensorFlow 中,您可以使用该tf.reduce_mean()函数来计算所有样本的预测值和真实值之间的绝对差的平均值。
9.3 在 PyTorch 中的实现
import torchdef l1_loss(y_pred, y_true):loss = torch.mean(torch.abs(y_pred - y_true))return loss 在 PyTorch 中,您可以使用该torch.mean()函数来计算所有样本的预测值和真实值之间的绝对差的平均值。
十、胡贝尔损失
Huber 损失是回归任务中使用的损失函数,与均方误差 (MSE) 损失相比,它对异常值的敏感度较低。它被定义为 MSE 损失和平均绝对误差 (MAE) 损失的组合,其中损失函数对于小误差为 MSE,对于较大误差为 MAE。这使得 Huber 损失比 MSE 损失对异常值更加稳健。
Huber损失函数定义如下:
L(y_pred, y_true) = 1/n * sum(0.5 * (y_pred - y_true)^2) if |y_pred - y_true| <= delta1/n * sum(delta * |y_pred - y_true| - 0.5 * delta^2) otherwise 其中n是样本数,y_pred是预测值,y_true是真实值,delta是确定 MSE 和 MAE 损失之间切换阈值的超参数。
当 时|y_pred - y_true| <= delta,损失函数为 MSE 损失。当 时|y_pred - y_true| > delta,损失函数为 MAE 损失,斜率为delta。
在实践中,delta通常设置为平衡 MSE 和 MAE 损失的值,例如1.0。
10.1 Numpy 中的实现
import numpy as npdef huber_loss(y_pred, y_true, delta=1.0):error = y_pred - y_trueabs_error = np.abs(error)quadratic = np.minimum(abs_error, delta)linear = (abs_error - quadratic)return np.mean(0.5 * quadratic ** 2 + delta * linear) 该函数将预测值y_pred、真实值y_true和delta超参数作为输入,并返回 Huber 损失。
该函数首先计算预测值和真实值之间的绝对误差,然后根据超参数将误差分成两个分量delta。二次分量是 时的 MSE 损失abs_error <= delta,线性分量是 时的 MAE 损失abs_error > delta。最后,该函数返回所有样本的平均 Huber 损失。
您可以在基于 numpy 的回归任务中使用此函数,方法是使用预测值、真实值以及所需值调用它delta。
10.2 在 TensorFlow 中的实现
import tensorflow as tfdef huber_loss(y_pred, y_true, delta=1.0):error = y_pred - y_trueabs_error = tf.abs(error)quadratic = tf.minimum(abs_error, delta)linear = (abs_error - quadratic)return tf.reduce_mean(0.5 * quadratic ** 2 + delta * linear) 该函数将预测值y_pred、真实值y_true和delta超参数作为输入,并返回 Huber 损失。
该函数首先使用 函数计算预测值和真实值之间的绝对误差tf.abs,然后delta使用tf.minimum和-运算符根据超参数将误差分成两个分量。二次分量是 时的 MSE 损失abs_error <= delta,线性分量是 时的 MAE 损失abs_error > delta。最后,该函数返回使用该函数的所有样本的平均 Huber 损失tf.reduce_mean。
您可以在基于 TensorFlow 的回归任务中使用此函数,方法是使用预测值、真实值以及所需的增量值delta调用该函数。
10.3 在 PyTorch 中的实现
import torch.nn.functional as Fdef huber_loss(y_pred, y_true, delta=1.0):error = y_pred - y_trueabs_error = torch.abs(error)quadratic = torch.min(abs_error, delta)linear = (abs_error - quadratic)return 0.5 * quadratic ** 2 + delta * linear该函数将预测值 y_pred、真实值 y_true 和 delta 超参数作为输入,并返回 Huber 损失。
该函数首先使用 torch.abs 函数计算预测值和真实值之间的绝对误差,然后使用 torch.min 和 - 运算符根据 delta 超参数将误差拆分为两个分量。二次分量是当abs_error <= delta时的MSE损失,线性分量是当abs_error > delta时的MAE损失。最后,该函数使用公式 0.5 * quadratic ** 2 + delta * linear返回 Huber 损失。
您可以在基于 PyTorch 的回归任务中使用此函数,方法是使用预测值、真实值以及所需的增量值调用该函数。阿琼·萨卡
相关文章:

深度学习在 NumPy、TensorFlow 和 PyTorch 中实现所有损失函数
目录 一、说明 二、内容提示 三、均方误差 (MSE) 损失 3.1 NumPy 中的实现 3.2 在 TensorFlow 中的实现 3.3 在 PyTorch 中的实现 四、二元交叉熵损失 4.1 NumPy 中的实现 4.2 在 TensorFlow 中的实现 4.3 在 PyTorch 中的实现 五、加权二元交叉熵损失 5.1 分类交叉熵损失 5.2 …...
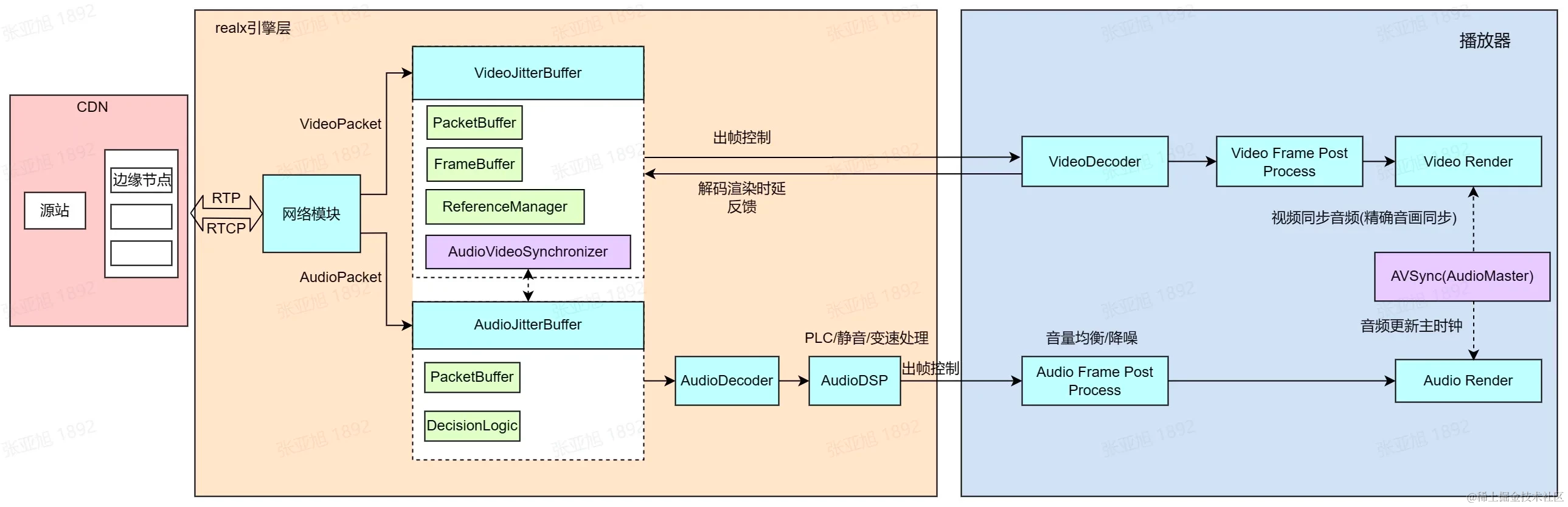
超低延时直播技术演进之路-进化篇
一、概述 网络基础设施升级、音视频传输技术迭代、WebRTC 开源等因素,驱动音视频服务时延逐渐降低,使超低延时直播技术成为炙手可热的研究方向。实时音视频业务在消费互联网领域蓬勃发展,并逐渐向产业互联网领域加速渗透。经历了行业第一轮的…...

相机坐标系之间的转换
一、坐标系之间的转换 一个有4个坐标系:图像坐标系、像素坐标系、相机坐标系、世界坐标系。 1.图像坐标系和像素坐标系之间的转换 图像坐标系和像素坐标系在同一个平面,利用平面坐标系之间的转换关系可以之知道两个坐标系变换的公式,并且该…...
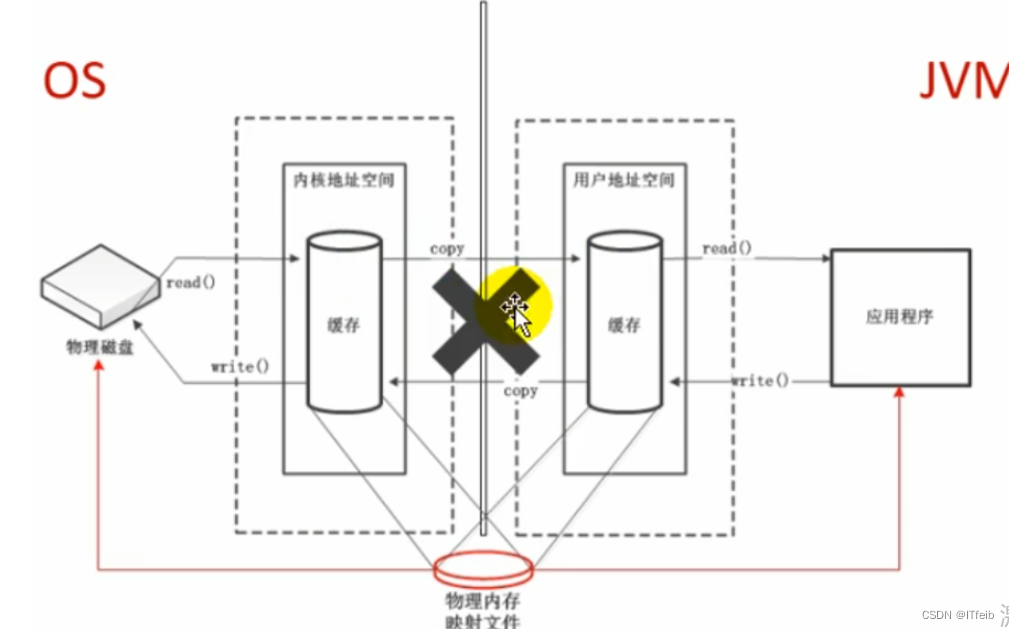
jvm--对象实例化及直接内存
文章目录 1. 创建对象2. 对象内存布局3. 对象的访问定位4. 直接内存(Direct Memory) 1. 创建对象 创建对象的方式: new最常见的方式、Xxx 的静态方法(单例模式),XxxBuilder/XxxFactory 的静态方法Class 的…...

【数据结构与算法】如何对快速排序进行细节优化以及实现非递归版本的快速排序?
君兮_的个人主页 即使走的再远,也勿忘启程时的初心 C/C 游戏开发 Hello,米娜桑们,这里是君兮_,国庆长假结束了,无论是工作还是学习都该回到正轨上来了,从今天开始恢复正常的更新频率,今天为大家带来的内容…...

【电商API接口的应用:电商数据分析入门】初识Web API(一)
如何使用Web应用变成接口(API)自动请求网站到特定信息而不是整个网站,再对这些信息进行可视化。由于这样编写到程序始终使用最新到数据来生成可视化,因此即便数据瞬息万变,它呈现到信息也都是最新的。 使用Web API Web API是网站的一部分&am…...

大运新能源天津车展深度诠释品牌魅力 为都市人群打造理想车型
如今,新能源汽车行业发展潜力巨大,不断吸引无数车企入驻新能源汽车赛道,而赛道的持续紧缩也让一部分车企很难找到突破重围的机会。秉持几十年的造车经验,大运新能源凭借雄厚的品牌实力从一众车企中脱颖而出。从摩托车到重卡&#…...
的应用)
深入浅出:react高阶成分(HOC)的应用
React中的HOC(Higher-Order Component)是一种高阶组件的模式,它是一个函数,接收一个组件作为参数,并返回一个新的包装组件。HOC可以用于增强组件的功能,例如添加属性、处理生命周期方法、共享状态等。 HOC…...

分库分表(3)——ShardingJDBC实践
一、ShardingSphere产品介绍 Apache ShardingSphere 是一套开源的分布式数据库中间件解决方案组成的生态圈,它由 JDBC、Proxy 和 Sidecar(规划中)这 3 款相互独立,却又能够混合部署配合使用的产品组成。 它们均提供标准化的数据分…...

Xcode 15下,包含个推的项目运行时崩溃的处理办法
升级到Xcode15后,部分包含个推的项目在iOS17以下的系统版本运行时,会出现崩溃,由于崩溃在个推Framework内部,无法定位到具体代码,经过和个推官方沟通,确认问题是项目支持的最低版本问题。 需要将项目的最低…...
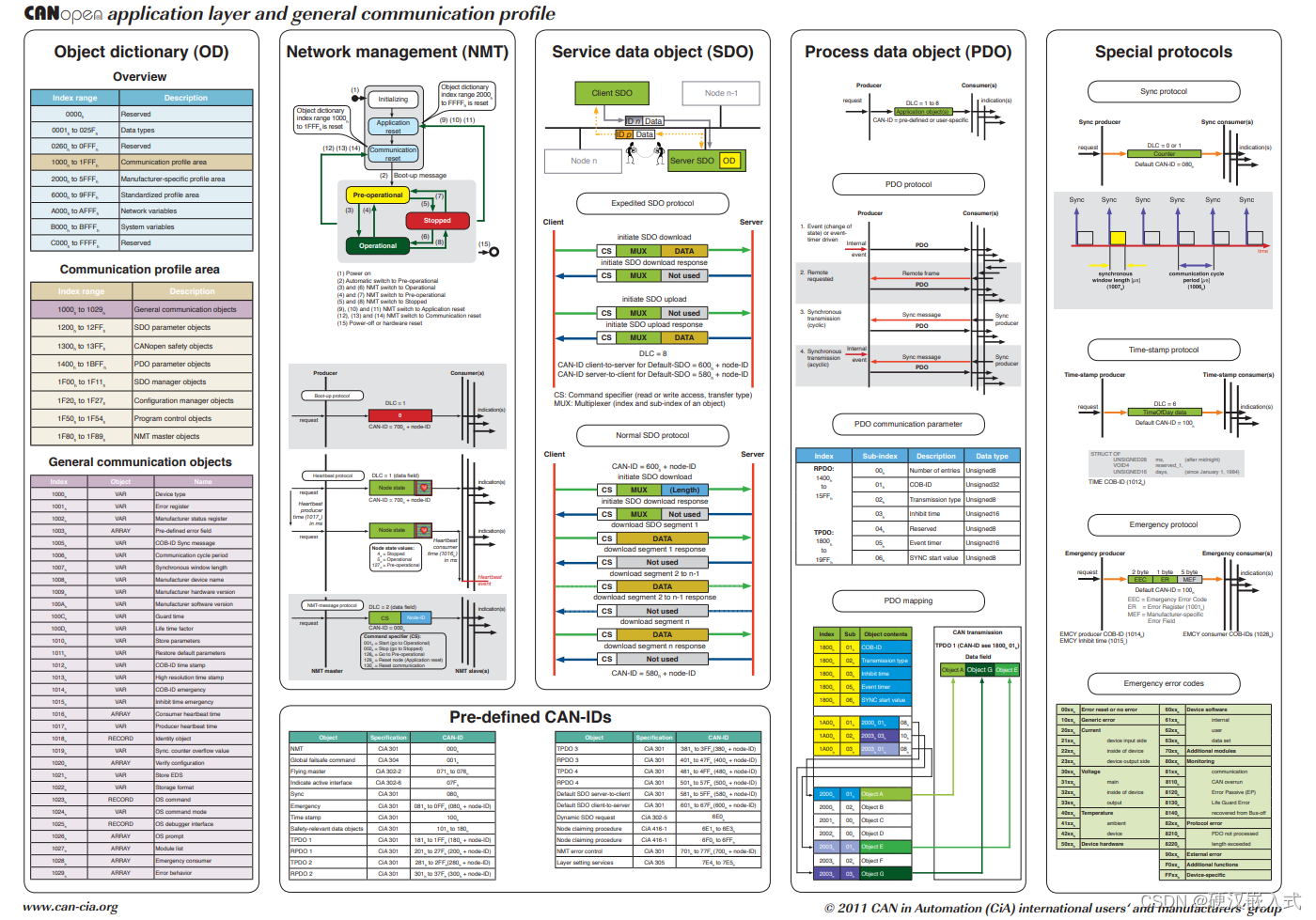
《安富莱嵌入式周报》第324期:单对以太网技术实战,IROS2023迪士尼逼真机器人展示,数百万模具CAD文件下载,闭环步进电机驱动器,CANopen全解析
周报汇总地址:嵌入式周报 - uCOS & uCGUI & emWin & embOS & TouchGFX & ThreadX - 硬汉嵌入式论坛 - Powered by Discuz! 更新一期视频教程: 第8期ThreadX视频教程:应用实战,将裸机工程移植到RTOS的任务划分…...

Kafka集群架构设计原理详解
从 Zookeeper 数据理解 Kafka 集群工作机制 这一部分主要是理解 Kafka 的服务端重要原理。但是 Kafka 为了保证高吞吐,高性能,高可扩展的三高架构,很多具体设计都是相当复杂的。如果直接跳进去学习研究,很快就会晕头转向。所以&am…...

学习Kotlin编程语言
官网地址 https://developer.android.google.cn/kotlin/learn?hlzh-cn 脑图...

js文字逐个显示
定时器每隔一段时间,替换文本内容,,substring 截取更多的字符串显示 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title> </head> <body…...

电子沙盘数字沙盘大数据人工智能开发教程第16课
电子沙盘数字沙盘大数据可视化GIS系统开发教程第16课:新增加属性在MTGIS3d控件 public bool ShowFLGrid;//是否显 示方里网格。 public bool Atmosphere;//是否显示大气圈。(因为WPF不支持shader功能,所以效果嘛。。。) 在SDK中为…...
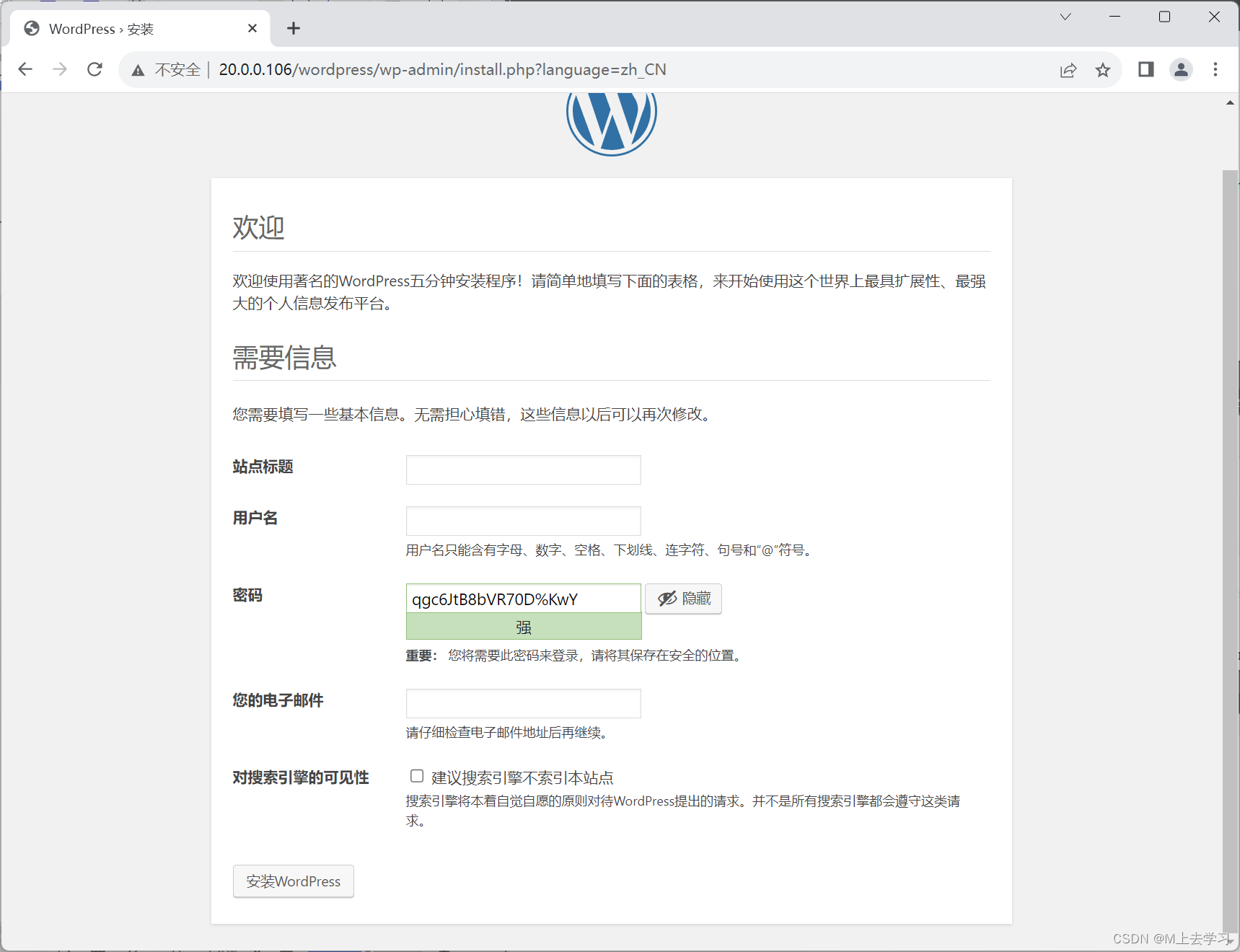
dockerfile lnmp 搭建wordpress、docker-compose搭建wordpress
-----------------安装 Docker--------------------------- 目前 Docker 只能支持 64 位系统。systemctl stop firewalld.service setenforce 0#安装依赖包 yum install -y yum-utils device-mapper-persistent-data lvm2 --------------------------------------------------…...
手写模拟SpringBoot核心流程
通过手写模拟实现一个Spring Boot,让大家能以非常简单的方式就能知道Spring Boot大概是如何工作的。 依赖 建一个工程,两个Module: 1.springboot模块,表示springboot框架的源码实现 2.user包,表示用户业务系统,用来写…...
怒刷LeetCode的第26天(Java版)
第一题 题目来源 64. 最小路径和 - 力扣(LeetCode) 题目内容 解决方法 方法一:动态规划 可以使用动态规划来解决这个问题。 首先创建一个与网格大小相同的二维数组dp,用于存储从起点到每个位置的最小路径和。然后初始化dp[0…...

Linux文件基本权限
一、Linux权限 简介 在Linux系统中,每个文件和目录都有读(r),写(w)和执行(x)权限,这些权限决定了用户对该文件或目录的访问方式。Linux服务器上有严格的权限等级,如果权限过高导致误操作会增加服务器的风险。文件权限 只有root用户和文件拥有者才可以修改文件访问权…...
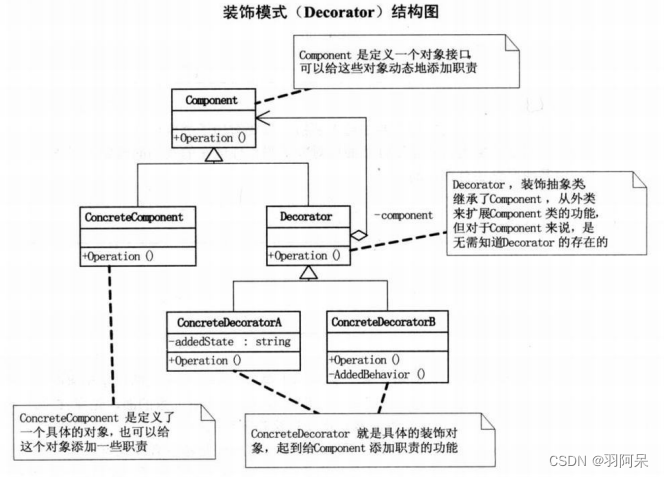
Unity设计模式——装饰模式
装饰模式(Decorator),动态地给一个对象添加一些额外的职责,就增加功能来说,装饰模式比生成子类更为灵活。 Component类: abstract class Component : MonoBehaviour {public abstract void Operation(); …...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...
