【管理运筹学】第 9 章 | 网络计划(2,时间参数的计算 —— 工作时间的确定与事项的时间参数)
文章目录
- 引言
- 一、工作时间的确定
- 二、事项的时间参数
- 2.1 事项的最早开始时间
- 2.2 事项的最迟结束时间
- 2.3 事项的时差
- 2.4 利用事项的时间参数来确定关键线路
引言
计算网络图中有关的时间参数,主要目的是找到关键线路,为网络计划的优化、调增和执行提供明确的时间概念。
网络图的时间参数,包括工作所需时间、事项最早、最迟时间、工作的最早、最迟时间及时差等等。进行时间参数的计算不仅可以得到关键线路,确定和控制整个任务在正常进度下的最早完工期,而且在掌握非关键工作基础上可进行人、财、物等资源的合理安排,进行网络计划的优化。
一、工作时间的确定
工作 ( i , j ) (i,j) (i,j) 的所需工时可记为 t ( i , j ) t(i,j) t(i,j) ,有以下两种确定办法。
(1)确定型网络。在具备工时定额和劳动定额的任务中,工作的工时 t ( i , j ) t(i,j) t(i,j) 可以用这些定额资料确定。有些工作虽然无定额可查,但也可以通过分析有关工作的统计资料来确定。
(2)概率型网络。对于开发性、试制性的任务,往往不具备(1)中的资料,可以采用三点时间估计法来确定工作的工时。这种方法需要先作出下面三种情况的时间估计:
a a a —— 最快可能完成时间(最乐观时间); m m m 最可能完成时间; b b b 最慢可能完成时间(最悲观时间)。
利用 3 个时间 a , b , m a,b,m a,b,m 每项工作的期望工时可估计为 t ( i , j ) = a + 4 m + b 6 . t(i,j)=\frac{a+4m+b}{6}. t(i,j)=6a+4m+b. 方差估计为 σ 2 = ( b − a 6 ) 2 . \sigma_2=\big(\frac{b-a}{6}\big)^2. σ2=(6b−a)2. 华罗庚教授对上述两个式子的由来有以下说明:由实际工作情况表明,工作进行时出现最顺利和最不顺利的情况都比较少,更多的是在最可能完成的时间内完成,工时的分布近似服从正态分布。假定 m m m 的可能性两倍于 a a a 或 b b b 的可能性,应用加权平均法。
在 ( a , m ) (a,m) (a,m) 之间的可能性均值为 ( a + 2 m ) / 3 (a+2m)/3 (a+2m)/3 ,在 ( m , b ) (m,b) (m,b) 之间的可能性均值为 ( 2 m + b ) / 3 (2m+b)/3 (2m+b)/3 ,则工时可以用上述两种情况各 0.5 的概率分布来描述,计算其期望和方差即可到上述两式。
关于工作的其他时间参数计算原则和上述类似。
二、事项的时间参数
事项本身并不占用时间,它只表示某项工作应在某一时刻开始或结束。对箭尾事项来说,它表示以此事项为起始的各项工作的开始,因而存在最早可能开始的时间;对箭头事项来说,它表示以此事项为完结的各项工作的结束,因而存在最迟必须结束的时间。可见,事项的时间参数有事项的最早开始时间、最迟结束时间以及二者的差值 —— 事项的时差。
2.1 事项的最早开始时间
事项的最早开始时间,是指的从该事项开始的各项工作的最早开工时间。事项 i i i 的最早开始时间用 t E ( i ) t_E(i) tE(i) 表示, E E E 表示 early 吧。
事项的最早开始时间是从网络图的起始事项算起,按照事项的编号顺序,从小到大,逐个计算,直到终止事项为止。一般地,指定网络起始事项的最早开始时间为 0 ,即 t E ( 1 ) = 0 t_E(1)=0 tE(1)=0 。
其他事项的最早开始时间都是相对于起始事项在零时刻开始的时间,计算公式为 t E ( j ) = max { t E ( i ) + t ( i , j ) ∣ i 为射入 j 事项的箭线的箭尾事项的编号 } ( j = 2 , 3 , ⋯ , n ) t_E(j)=\max\{t_E(i)+t(i,j) \big| i 为射入j事项的箭线的箭尾事项的编号\}(j=2,3,\cdots,n) tE(j)=max{tE(i)+t(i,j) i为射入j事项的箭线的箭尾事项的编号}(j=2,3,⋯,n) 事项的最早开始时间算出后,写在网络图上该事项的上方或下方,用方框 [ ] [] [] 框起来表示,里面写上最早开始时间。
假设网络计划图如下图所示(图片来源:知乎-运筹说)。

则各事项的最早开始时间为: t E ( 1 ) = 0 , t E ( 2 ) = t E ( 1 ) + t ( 1 , 2 ) = 0 + 4 = 4 , t E ( 3 ) = t E ( 2 ) + t ( 2 , 3 ) = 4 + 6 = 10 , t E ( 4 ) = max { t E ( 2 ) + t ( 2 , 4 ) , t E ( 3 ) + t ( 3 , 4 ) } = max { 4 + 3 , 10 + 8 } = 18 , ⋯ , t E ( 10 ) = 32 t_E(1)=0,t_E(2)=t_E(1)+t(1,2)=0+4=4,t_E(3)=t_E(2)+t(2,3)=4+6=10,t_E(4)=\max\{t_E(2)+t(2,4),t_E(3)+t(3,4)\}=\max\{4+3,10+8\}=18,\cdots, t_E(10)=32 tE(1)=0,tE(2)=tE(1)+t(1,2)=0+4=4,tE(3)=tE(2)+t(2,3)=4+6=10,tE(4)=max{tE(2)+t(2,4),tE(3)+t(3,4)}=max{4+3,10+8}=18,⋯,tE(10)=32 。
2.2 事项的最迟结束时间
事项的最迟结束时间是指,在不拖延总工期的前提下,以该事项为结束的各项工作最迟必须完成的时间。用 t L ( i ) t_L(i) tL(i) 表示事项 i i i 的最迟结束时间。
事项的最迟结束时间是从网络图的终止事项算起,按照事项编号的逆序,由大到小,逐个计算,知道起始事项为止。因为网络图的终止事项无后续工作,而且事项本身又不占时间,所以网络图的终止事项的最迟结束时间与它的最早开始时间应该相等,即 t E ( n ) = t L ( n ) t_E(n)=t_L(n) tE(n)=tL(n) 。
如果对某项工程或任务有规定的完成时间要求,终止事项的最迟结束时间应取这个时间值 —— 规定的目标工期。
各事项最迟结束时间计算方法为: t L ( i ) = min { t L ( j ) − t ( i , j ) ∣ j 为从 i 事项射出的箭线的箭头事项编号 } ( i = n − 1 , n − 2 , ⋯ , 1 ) t_L(i)=\min\{t_L(j)-t(i,j)\big|j为从i事项射出的箭线的箭头事项编号\}(i=n-1,n-2,\cdots,1) tL(i)=min{tL(j)−t(i,j) j为从i事项射出的箭线的箭头事项编号}(i=n−1,n−2,⋯,1) 事项的最迟结束时间算出后,写在网络图中该事项最早开始时间右侧的近旁,用 △ \triangle △ 框起来。
上面的例子中,各事项的最迟结束时间为: t L ( 10 ) = 32 , t L ( 9 ) = 31 , t L ( 8 ) = 26 , t L ( 7 ) = min { t L ( 9 ) − t ( 7 , 9 ) , t L ( 8 ) − t ( 7 , 8 ) } = min { 31 − 8 , 26 − 2 } = 23 , ⋯ , t L ( 1 ) = 0 t_L(10)=32,t_L(9)=31,t_L(8)=26,t_L(7)=\min\{t_L(9)-t(7,9),t_L(8)-t(7,8)\}=\min\{31-8,26-2\}=23,\cdots,t_L(1)=0 tL(10)=32,tL(9)=31,tL(8)=26,tL(7)=min{tL(9)−t(7,9),tL(8)−t(7,8)}=min{31−8,26−2}=23,⋯,tL(1)=0 。
2.3 事项的时差
事项的时差又称事项的机动时间、事项的宽裕时间,是指在不影响总工期按时完成时,该事项可以推迟的最大机动时间。计算方法为 Δ t ( i ) = t L ( i ) − t E ( i ) \Delta t(i)=t_L(i)-t_E(i) Δt(i)=tL(i)−tE(i) 。特别地,时差为 0 的事项称为关键事项。时差一般不标在网络图上,很轻易就能计算出来。
2.4 利用事项的时间参数来确定关键线路
把网络图中所有线路的路长都计算出来,找到最大的那一条即为关键线路,这种方法称为穷举法。
还有一种利用事项的时间参数来寻找关键线路的方法:连接关键事项的工作若满足: t E ( j ) − t E ( i ) = t L ( j ) − t L ( i ) = t ( i , j ) t_E(j)-t_E(i)=t_L(j)-t_L(i)=t(i,j) tE(j)−tE(i)=tL(j)−tL(i)=t(i,j) 则由此形成的线路即为关键线路。
相关文章:

【管理运筹学】第 9 章 | 网络计划(2,时间参数的计算 —— 工作时间的确定与事项的时间参数)
文章目录 引言一、工作时间的确定二、事项的时间参数2.1 事项的最早开始时间2.2 事项的最迟结束时间2.3 事项的时差2.4 利用事项的时间参数来确定关键线路 引言 计算网络图中有关的时间参数,主要目的是找到关键线路,为网络计划的优化、调增和执行提供明…...

英语——方法篇——单词——羊肉串记忆法——单词密码
在记忆英语单词的时候,我们习惯于一个字母一个字母地记忆,很少会以词或字母组合为单位来记忆。在这里我们要打开视野,学习以词或字母组合为单位,一组一组地记忆英语单词。英语单词数目庞大,但是构成单词的字母只有26个…...

【m98】视频帧的 jitterbuffer 1:
VCMJitterBuffer D:\XTRANS\m98_rtc\rtc-webrtc\src\modules\video_coding\jitter_buffer.h使用2个map和一个list管理VCMFrameBuffer 指针对象:UnorderedFrameList free_frames_ RTC_GUARDED_BY(mutex_);FrameList decodable_frames_ RTC_GUARDED_BY(mutex_);FrameList incomp…...

javascript中map和filter的区别与联系
javascript中map和filter的区别与联系如何获取对象数组中某个值 javascript中map和filter的区别与联系 在 JavaScript 中,map 和 filter 是两个常用的数组方法,用于对数组进行转换和过滤操作。它们的区别和联系如下: 功能不同: m…...
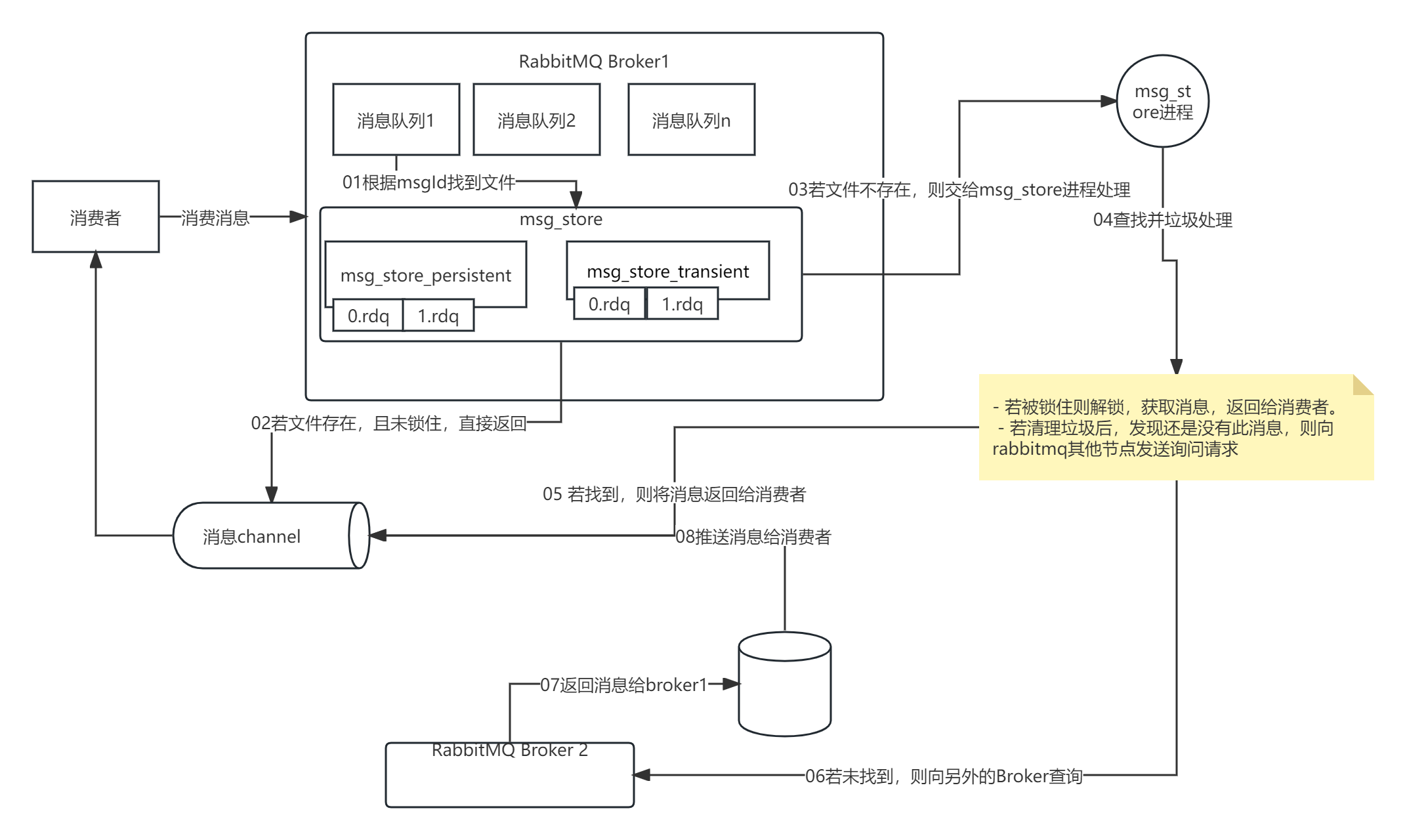
【RabbitMQ 实战】10 消息持久化和存储原理
一、持久化 1.1 持久化对象 rabbitmq的持久化分为三个部分: 交换器的持久化。队列的持久化。消息的持久化。 1.1.1 交换器持久化 交换器的持久化是通过在声明交换器时, 指定Durability参数为durable实现的。若交换器不设置持久化,在rabb…...
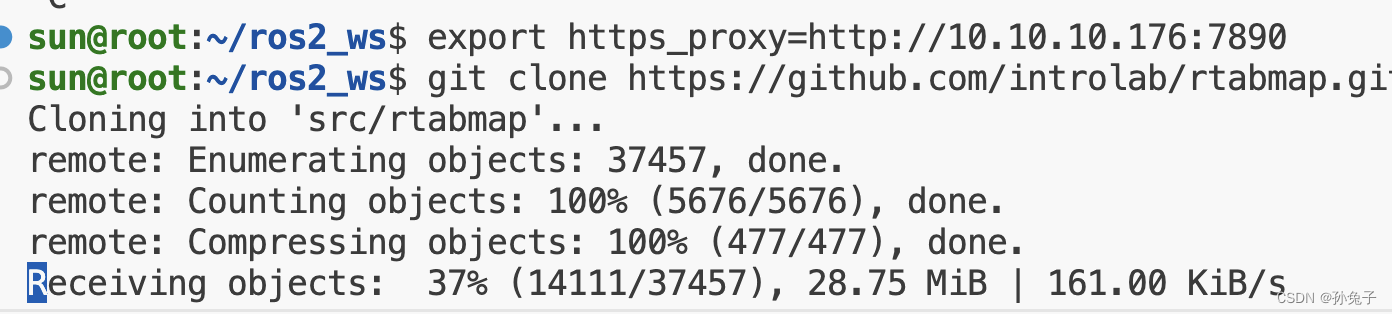
vscode 连接ubuntu git下载缓慢
在ubuntu20.04下载: git clone https://github.com/introlab/rtabmap.git src/rtabmap 挂掉情况 export https_proxyhttp://10.10.10.176:7890export http_proxyhttp://10.10.10.176:7890 其中 10.10.10.176是我本机的ip地址,7890是我的代理后几位 如…...

2731. 移动机器人
2731. 移动机器人有一些机器人分布在一条无限长的数轴上,他们初始坐标用一个下标从 0 开始的整数数组 nums 表示。当你给机器人下达命令时,它们以每秒钟一单位的速度开始移动。 给你一个字符串 s ,每个字符按顺序分别表示每个机器人移动的方…...

小程序实现人脸识别功能
调用api wx.startFacialRecognitionVerify 第一步: // 修改方法expertUpdate() {wx.startFacialRecognitionVerify({name: _this.registerForm.realName, //身份证名称idCardNumber: _this.registerForm.idCard, //身份证号码checkAliveType: 1, //屏幕闪烁(人脸核验的交互…...

【】javax.crypto.IllegalBlockSizeException: Input length not multiple of 8 bytes
问题描述 jdk版本:8 用DES进行加解密,其中转换模式为“DES/CBC/NoPadding”,要加密的明文为 “密码学浅析”,执行加密操作,报如下错误 Exception in thread "main" javax.crypto.IllegalBlockSizeExcepti…...
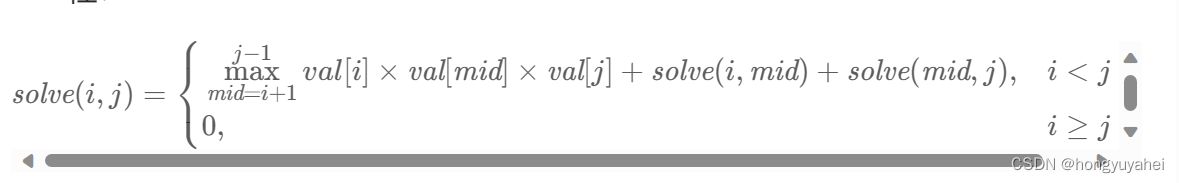
312.戳气球
将戳气球转换到添加气球,记忆搜索slove(i,j):在开区间(i,j)全部填满气球得到的最多硬币数,两端val[i]、val[j] class Solution { public:vector<vector<int>> ans;vector<int> val;int slove(int left,int right){if(left&…...

get_trade_detail_data函数使用
查阅股票持仓情况 positions get_trade_detail_data(‘8000000213’, ‘stock’, ‘position’) for dt in positions: print(f’股票代码: {dt.m_strInstrumentID}, 市场类型: {dt.m_strExchangeID}, 证券名称: {dt.m_strInstrumentName}, 持仓量: {dt.m_nVolume}, 可用数量:…...
【融合ChatGPT等AI模型】Python-GEE遥感云大数据分析、管理与可视化及多领域案例实践应用
目录 第一章 理论基础 第二章 开发环境搭建 第三章 遥感大数据处理基础与ChatGPT等AI模型交互 第四章 典型案例操作实践 第五章 输入输出及数据资产高效管理 第六章 云端数据论文出版级可视化 更多应用 随着航空、航天、近地空间等多个遥感平台的不断发展,近…...

LeetCode862 和至少为k的最短子数组
题目: 解析: 1、先构造前缀和数组 2、单调队列存放滑动窗口,目的求Sj-Si >k的情况下,窗口最小。 代码: class Solution {public int shortestSubarray(int[] nums, int k) {int n nums.length;long[] sums new …...

网卡bonding模式 - bond模式配置介绍
网卡bonding简介 网卡绑定就是把多张物理网卡通过软件虚拟成一个虚拟的网卡,配置完毕后,所有的物理网卡的ip和mac将会变成相同的。多网卡同时工作可以提高网络速度,还可以实现网卡的负载均衡、冗余。 bonding模式 1 round-robin(mode0) 轮转…...

做了个 chrome 插件实现 B 站视频截图功能,直接从当前视频帧无损复制
起因是看 B 站视频想截个图很麻烦,右下角暂停按钮无法去除,于是写了一行代码把暂停按钮隐藏。 后经提醒,发现可以通过 canvas 获取视频帧来截取图片,于是写了如下代码完美获取视频帧。 var v document.querySelector(".bpx…...

Docker linux 安装
sudo yum update sudo yum clean all sudo yum makecache#安装依赖 sudo yum install -y yum-utils device-mapper-persistent-data lvm2 #添加官方存储库 sudo yum-config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo#安装-跳过一些异常依赖…...
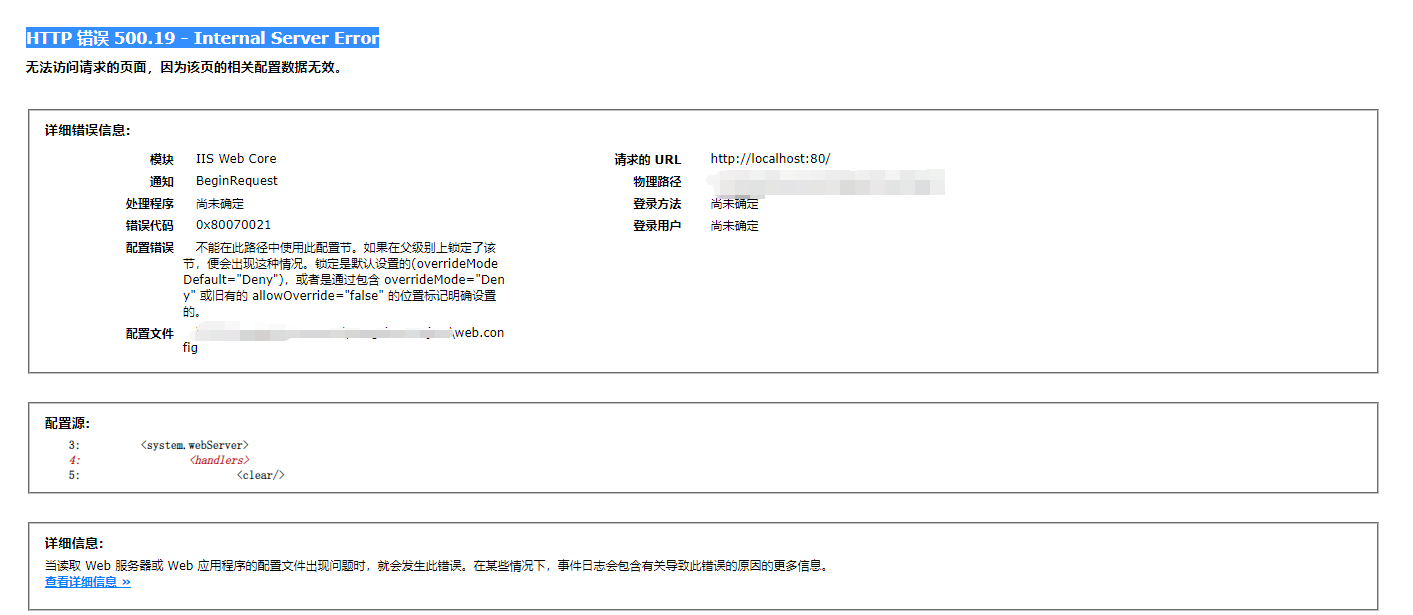
windows部署django服务器
windows部署django服务器 1、安装IIS1.1 控制面板-----程序----程序和功能----启用或关闭windows功能1.2安装IIS服务器,完成后,重新进入,把CGI安装进系统 2、安装python与虚拟环境2.1 安装python2.2 安装virtualenv虚拟环境2.3 创建一个虚拟环…...

ChatGPT prompt汇总-个人使用-持续更新....
用途 学术写作更新记录 学术写作 中译英(GPT-4) I am a researcher studying deep learning and now trying to revise my manuscript which will be submitted to the Journal of Nature . I want you to act as a scientific English-Chinese translator, I will provide yo…...
Vue实现简单的接口封装
1. 在src中创建一个api文件夹 2. 按功能、模块等新建对应的js文件 3. 在内部写对应的封装接口,并导出 import axios from "axios";/*** 接口名称:* 接收参数:* 返回参数:* */export const miens ()>{return new P…...

软件测试工具有什么作用?有哪些好用的测试工具推荐?
软件测试工具是现代软件测试中不可或缺的重要组成部分,指的是一系列在软件开发过程中使用的工具,用于帮助测试人员进行测试活动,提高测试效率,减少测试成本。选择并使用合适的软件测试工具,可提高软件质量和效率。 一…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...
